静压桩沉桩过程中贯入机理理论研究进展*

2022-05-11刘雪颖王永洪张明义白晓宇

工程地质学报 2022年2期

刘雪颖王永洪② 张明义② 白晓宇②

(①青岛理工大学土木工程学院，青岛 266033，中国)(②山东省高等学校蓝色经济区工程建设与安全协同创新中心，青岛 266033，中国)

0 引言

在我国的沿海和南方地区，存在较多的深厚软弱地基(赵梦怡等，2018；高英等，2019；李高山等，2019；毛洪运等，2019)。在实际工程中，多采用桩基础对其进行加固处理，而静压桩凭借着无噪音，无振动，无冲击力，施工应力小等诸多优点，在我国的应用越来越广泛，成为了软土地区广泛采用的一种沉桩形式(White et al.，2002；Fattah et al., 2016；张明义等，2017；Murthy et al.，2018；王永洪等，2018)。

相较于打入桩，静压桩的贯入较为稳定，但在沉桩过程中，下部土体会产生侧向移动，地表抬升，属于挤土桩(何耀辉，2005)。在静压沉桩过程中，由于桩周土体短时间内的不可压缩性，会使土体中产生较高的超孔隙水压力，从而产生挤土效应，造成桩身弯曲、倾斜、水平位移等，给工程带来不良影响(王瑞彩等，2015)。但静压沉桩的贯入机理受压桩力、沉桩速度、土层、地下水等因素共同影响，对其贯入机理的研究还不够充分(樊向阳，2007)。因此，众学者基于理论分析对静压桩沉桩机理展开了一系列的研究。

目前，常用的静压沉桩研究方法有：模型试验法(李雨浓等，2010；刘清秉等，2011；张可能等，2012；曹兆虎等，2014；李镜培等，2018a)、原位试验法(罗战友等，2014；李林等，2017；王嘉勇等，2018；李镜培等，2018b；王永洪等，2019)、理论分析法(Bishop et al.，1945；Carter et al.，1979；Baligh，1985；汤斌等，2018)。模型试验法具有成本低、效率高、易于操作且所测数据针对性强等特点，成为诸多学者首选的研究方法，但模型试验中多采用均质土作为模型地基土，而实际工程中影响桩静力贯入机理的因素复杂，用模型试验进行分析的准确度较低(曹兆虎等，2014)；原位试验虽然所测数据真实可靠，但试验成本较高、耗时较长且现场操作难度大(李镜培等，2018b)；而理论分析法从静压桩贯入机理的本质出发，在原有的理论基础上进行修正与发展，可以获得贯入特性的本质机理(李月健，2001)。所以有许多学者选择理论分析法对静压沉桩的贯入机理进行研究，并取得了诸多成果。本文对静压沉桩贯入机理理论研究所用的圆孔扩张理论、应变路径法、有限元分析的研究成果和局限性及存在的问题进行介绍性总结和分析，并对其未来的发展方向进行展望。

1 圆孔扩张理论

圆孔扩张理论是由Bishop et al.(1945)提出，用于研究金属成型等问题，后逐渐应用于岩土方面的研究。首先，假设土体是理想的弹塑性体，材料服从Tresca或莫尔-库仑屈服准则，然后基于弹塑性理论，得出初始半径的柱(球)形孔被均布的内压力扩张后的通解，初始受力计算原理图如图1所示。经过Vesic(1972)、Randolph et al.(1979)、Carter et al.(1986)的不断发展，圆孔扩张理论已成为研究沉桩贯入机理最广泛的方法之一。

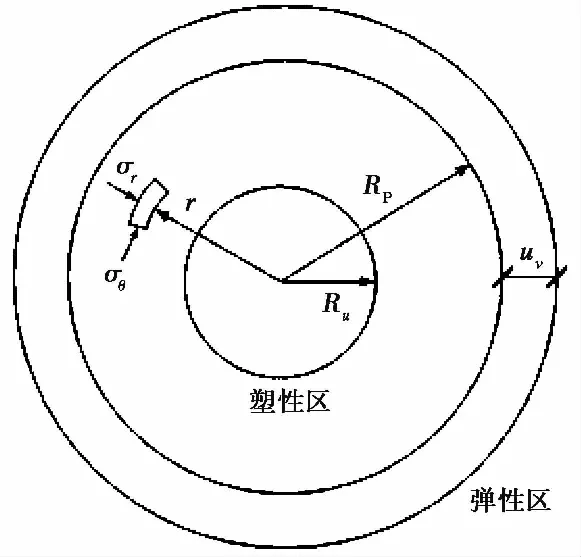
图1 圆孔扩张示意图(Bishop et al., 1945)

1.1 基于圆孔扩张求解沉桩阻力

在原有的圆孔扩张理论中，将剪切模量设定为常量，与实际情况不符。近年来，国内外学者通过圆孔扩张理论对沉桩阻力的计算方法进行了一定优化：Yu et al.(1991)在原有沉桩贯入机制的基础上，结合球孔扩张理论，同时加入Boussinesq解进行修正，获得了桩端阻力与桩侧摩阻力的计算公式。张明义等(2003b)通过对桩端部分采用球孔扩张理论解答，对桩侧部分采用滑动摩擦理论解答，建立了球孔扩张-滑动摩擦计算模式，分别计算了沉桩过程中的端阻力和侧摩阻力，其计算图式如图2所示。得到了实用准确的沉桩阻力计算公式。刘俊伟等(2009)结合球孔扩张与源-源假设理论，基于Boussinesq解修正的基础上，分别计算了桩端阻力和桩侧摩阻力，在考虑了侧阻退化情况下提出了压桩力的模拟计算公式，通过计算时桩侧土单元与桩底之间的距离来体现侧阻的退化效应，采用以下公式：

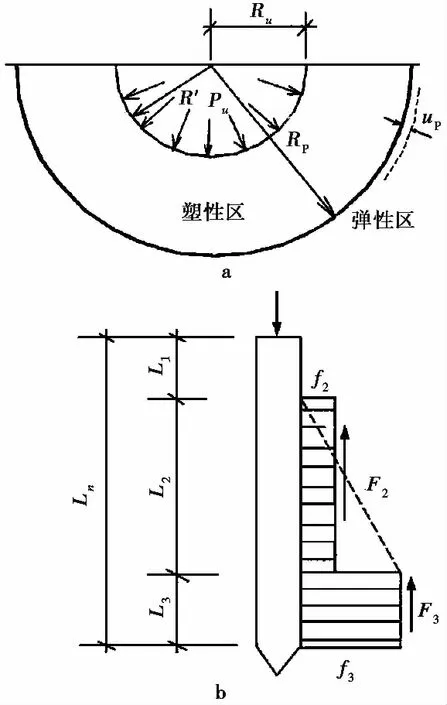
图2 沉桩阻力计算示意图(张明义等，2003b)

(1)

式中：τmax为桩第1次经过该单元的侧摩阻力；m为退化因子。

杨庆光等(2013)通过圆孔扩张理论，引入贯入深度对扩孔压力的作用，得出扩孔压力的迭代算法；并建立了楔形与等截面的静压沉桩阻力的计算公式。李林等(2016)通过使用K0各向异性修正剑桥(K0-MCC)模型，得到了静压沉桩柱孔扩张的基本解答，同时提出沉桩阻力的估算公式，其沉桩阻力由桩端阻力和桩侧阻力组成，沉桩阻力分布图如图3所示。阮永芬等(2017)基于圆孔扩张理论，研究了引入土体扰动修正系数下的齿形桩承载力，并探讨了桩周球孔扩张的影响，分析了有齿桩竖向与侧向承载力机理。Li et al.(2017)基于对桩周土体应力历史的考虑，对静压桩承载力进行了理论研究；通过求解控制方程，得到了桩周土体中有效应力的变化。

图3 沉桩阻力分布图(李林等，2016)

1.2 基于圆孔扩张求解桩侧压力与土体位移

另有部分学者基于圆孔扩张理论，对沉桩过程中的桩侧压力与桩侧土体位移进行了研究：Cao et al.(2001)利用修正剑桥模型和大变形理论，假定了不排水条件塑性区的偏应力，统一解答了圆孔扩张问题，获得了桩土界面径向应力与孔隙水压力的精确解。Sun et al.(2004)通过简化剑桥模型，引入了新的应力张量和硬化参数，得到了简化后的柱孔弹塑性扩张问题的解答，但未考虑柱孔扩张过程中有效应力之间的关系，且由于剑桥模型仅使用p和q两个应力参数，难以反映柱孔扩张中土体的三维强度特性。胡伟等(2006)以考虑土体体积变化为基础，应用圆孔扩张理论，结合修正剑桥模型，推导了非饱和土球孔扩张后应力和位移分布的解析解。同时分析了超固结比对应力、位移的影响。李镜培等(2014)结合修正剑桥模型，在偏应力无任何假设的条件下，得到了不排水条件下球孔周围土体应力和孔隙水压力的半解析解，并将球孔扩张应用于静力触探原位试验，提高了原位试验的拓展应用性。李林等(2016)通过使用K0各向异性修正剑桥(K0-MCC)模型，同时考虑天然饱和黏土的初始应力的各向异性、应力历史等特征，得到了静压沉桩柱孔扩张的基本解答，其桩周弹性区和塑性区位移解答分别为：

(2)

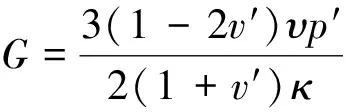
式中：G为土体的剪切模量；υ=1+e，为土体体积比；e为土体孔隙比；v′为有效泊松比。

σrx=σry+

(3)

Δurx=(pfx-p′f)-(p0-p′0)

(4)

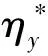
张亚国等(2018)在李林的基础上，在原有沉桩挤土位移解答方法中加入对土性弹塑性本构关系与地表边界效应的考虑，假定屈服后土体服从剑桥修正模型，推导出了无限长桩长的挤土位移初始解，并引入修正函数来表达地表边界和沉桩深度的影响，该修正函数为弹性区内挤土位移与圆柱孔弹性挤土位移之比f，即：

(5)

式中：h为总桩长；h1和h2分别为点到桩底和桩顶的竖向距离；dr为点到桩中心的水平距离。

周航等(2014)在圆孔扩张理论的基础上，提出了沉桩过程中桩周土体位移场和超孔隙水压力的理论方法。分析了楔入角、贯入深度和桩周土参数对挤土效应的影响。梅国雄等(2008)基于圆柱孔扩张理论，同时引入考虑位移的土压力计算方法确定由水平向应力诱发的侧压力系数的基础上，根据极限平衡理论推导出桩周浅层土体隆起分界面计算式为：

(6)

1.3 基于圆孔扩张求解开口管桩土塞效应

通过考虑土塞效应，可以利用圆孔扩张理论对开口管桩的贯入机理进行研究：郑俊杰等(2006)在考虑了土塞效应条件下，利用圆孔扩张理论对开口管桩的挤土效应进行了分析，得出了开口管桩桩周土体应力场与位移场的解析解。刘裕华等(2007)利用圆孔扩张理论分析了开口管桩的弹塑性力学，得到了塑性区半径和土体位移的表达式，同时关于土塞效应对开口管桩挤土效应的影响进行了探讨。黄生根等(2015)在弹塑性力学分析的基础上通过考虑管桩土塞效应的规律，得到了柱孔扩张过程中桩周土体的应力场及位移场的解析表达式为：

塑性区应力解：

(7)

弹性区应力解：

(8)

弹性区与塑性区边界处位移解：

(9)

弹性区位移解：

(10)

式中：R0为初始孔半径；Ru为孔扩张后的半径；r为半径；E为弹性模量；μ为泊松比；C为土体黏聚力；φ为土体内摩擦角；Δ为塑性区土体的平均体积应变；G为剪切模量。

1.4 基于圆孔扩张求解异形桩贯入机理

随着经济的不断发展，实际工程中静压桩的截面形状不断更新，已有学者对不同桩型静压桩的沉桩贯入机理进行了有益的研究：杨庆光等(2013)通过考虑扩孔深度对压力的影响，推导出扩孔压力的迭代算法。周航等(2014)在圆孔扩张理论的基础上，考虑到扩底楔形桩截面尺寸的变化情况，扩底楔形桩与普通楔形桩沉桩示意图如图4所示，提出了扩底楔形桩在静压沉桩过程中沉桩阻力的理论计算方法。并分析了楔形角、沉桩深度、土体参数等因素对沉桩阻力的影响。Manandhar et al.(2011，2013)通过荷载传递法中的迭代过程来计算表面摩擦，引入了压力-膨胀关系，提出了基于球孔扩张理论计算表面摩擦的公式；同时，引入渐锥角的影响来计算锥形桩的桩端阻力。阮永芬等(2017)基于圆孔扩张理论与土体扰动修正系数，研究了齿形桩的承载力，分析竖向及侧向承载力的机制，该齿形桩的总竖向力为：

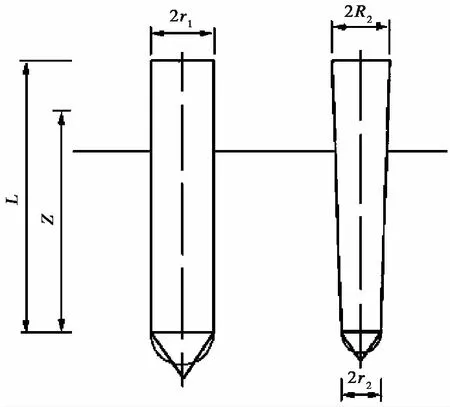
图4 沉桩示意图(周航等，2014)

(11)

(12)

f=αμσ

(13)

σ=σr+k0γz

(14)

(15)

τf=c+ασtanφ

(16)

式中：Wp为自重；Q0为桩顶压力；qh为桩端球孔应力；Fh为桩侧阻力；f为桩周摩阻力(基于扰动系数)；τ为齿形桩齿间抗剪切力；n为总齿间的个数；α为修正系数；σ为法向应力；σr为圆孔扩张应力；τf为桩间土体剪应力。

但是，经典的圆孔扩张理论存在着一个很大的缺点：其所得的解析解只考虑到径向坐标的影响，而未考虑竖向坐标的影响。直接将圆孔扩张理论应用于三维坐标体系中的沉桩过程，忽略了竖向摩擦力的影响，与实际应用情况不符。圆孔扩张理论在静压桩研究中的应用还需要进一步完善和优化。

2 应变路径法

Baligh(1985)于1985年提出了应变路径法，该法相对于圆孔扩张理论考虑了深度变化对土体位移的影响和桩贯入过程的连续性。应变路径法基于不考虑本构关系，可将扩展速度积分获得变形，然后进行微分得到应变。

部分国内外学者利用应变路径法对沉桩机理进行了一系列的研究，获得了一定成果。Baligh(1985)利用应变路径法为阐明和预测桩基础的行为、解释现场试验、评估取样扰动效应以及为处理“深部岩土问题”提供了一个完整和系统的框架。用应变路径法确定了渗透应力和孔隙压力，并将这些解决方案以近似的形式扩展到实际工程中。Sagaseta(1987)假设贯入过程中土体形成无限的速度场，运用点源和流场求解位移场，提出源-汇法，在不排水的沉桩过程中，可以认为，点源在无限土中匀速下沉形成一个圆柱孔，沉桩过程中在土的自由边界会产生正应力和剪应力。但由于修正应力引起的位移不考虑大变形的影响，对大变形的分析只考虑局部。罗战友(2004)通过运用源-源法，源-汇法对应变路径法进行了修正，将地表土体转变为半无限空间土体，修正了应变路径法的边界条件。应变路径法假定土为各向同性的无限体，忽略地表存在，这其实与自由表面的无约束边界条件是不一致的。其结果是，所有的土均会沉降，这与实际情况是矛盾的。汪敏等(2015)首先假设土壤是无限的，然后通过地表面处σ和τ的修正，消除虚拟边界条件，结合源-源，源-汇的相互作用，假定土体位移为小应变，得到静压管桩单桩竖向和水平挤土位移的解析解，其竖向与水平的求取步骤分别如图5，图6所示，并对其影响因素进行了研究。Zhou et al.(2018)基于应变路径法提出了一种新的通用分析方法来获取任意截面桩周土体的变形机理。采用一种新的二维(径向和周向)空腔扩展模型模拟侵彻问题，在应变路径法理论框架的基础上，利用保角变换技术，将非圆柱型空腔扩张的运动学(速度场)简化为求解具有任意速度边界条件的拉普拉斯方程。可以看出，近年来采用应变路径法对静压桩贯入特性进行研究的学者较少，这主要是因为该法计算较为繁琐。

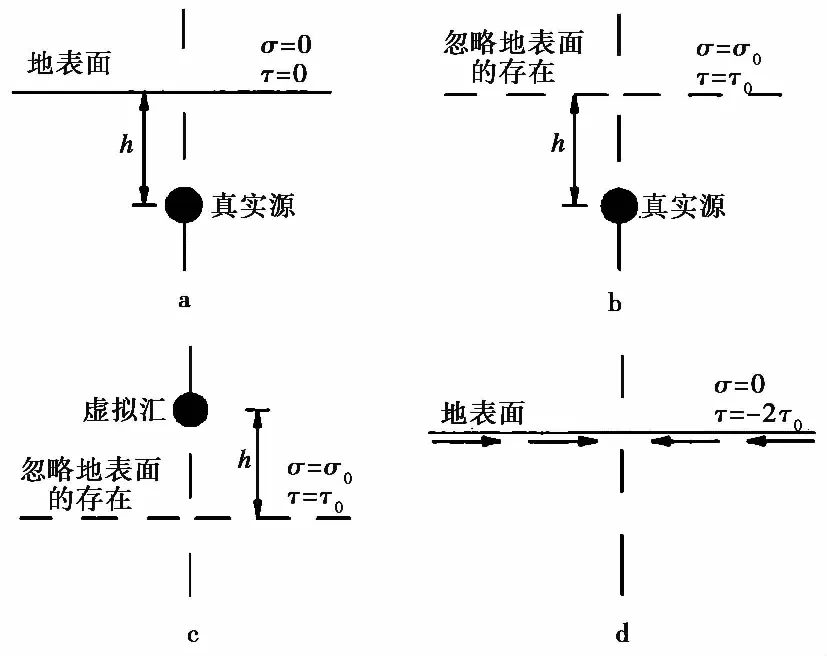
图5 垂直方向挤土位移(汪敏等，2015)

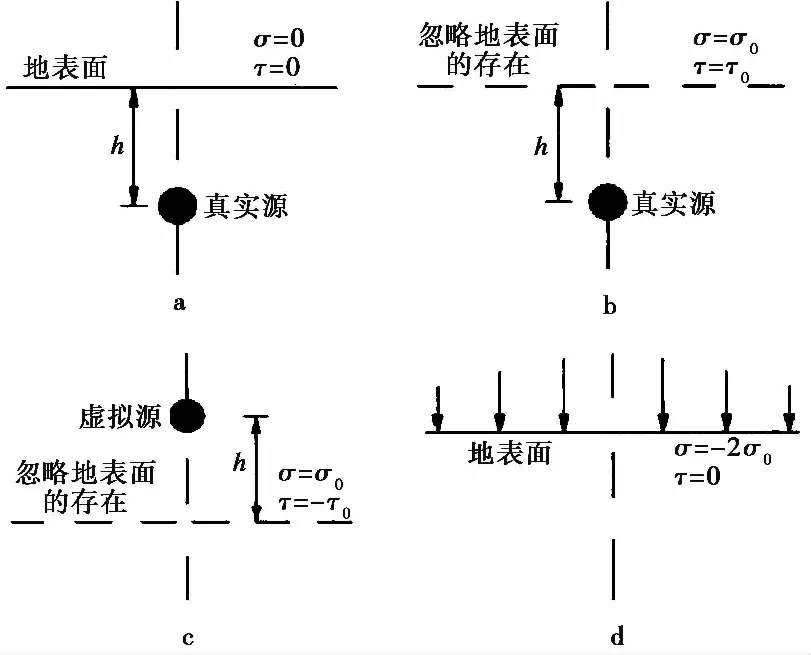
图6 水平方向挤土位移(汪敏等，2015)

对比圆孔扩张理论，应变路径法考虑深度的影响和沉桩的连续贯入性。可得到沉桩过程中的应力、位移与深度的大致分布规律，但本质上应变路径法为近似算法，计算步骤较为繁琐。同时将圆孔扩张理论与应变路径法相结合，可以互为补充。

3 有限单元法

有限元法由Carter et al.(1986)于1979年首次提出，在沉桩模拟中被广泛应用。对于桩体的有限元分析，主要分为小应变和大变形模型两种。小应变即小变形模型(Potts et al.，2001；Benz，2007)，所建模型中的孔洞为预先钻孔，再将桩体放入，其桩周土体仍处于初始应力状态；再以破坏荷载等于贯入阻力为计算基础，对其进行一个产生增量的塑性破坏计算。以小应变模型为基础所进行的模拟过程并不完全准确，这是因为在静力压桩过程中桩周将产生较大的桩侧应力，而在此计算模式下，所得桩侧应力远小于实际阻力。大变形模型通过考虑土体材料、几何双重非线性以及静力贯入对初始应力的影响，能够更为准确地模拟桩周土体的应力-应变情况。随着有限元分析的不断发展，目前国内外学者(Kiousis et al.，1988；王浩等，2002)多通过建立大变形模型进行沉桩模拟。

3.1 静压沉桩模型的建立与优化

近年来，国内外学者对基于有限元法的静力沉桩机理进行了一系列研究。Chopra et al.(1992)通过把沉桩过程模拟为土体逐渐劈裂过程，继而扩张到桩径，建立了静压桩沉桩模型。但该模型为小应变模型，未考虑桩-土相互作用的问题。Mabsout et al.(2003)在原有沉桩有限元模型的基础上，同时考虑桩-土作用，优化了原有模型，获得了基于新模型的计算式。但因采用了施加力荷载的方式，难以模拟整个沉桩过程，因此无法获得浅层地表处挤土效应的解答。罗战友等(2005)通过建立以有限变形理论及土体屈服准则为基础的压桩有限元模型(图7)，对静压桩沉桩产生的位移场进行了分析，得出了桩土模量比、桩土界面的摩擦特性及泊松比对沉桩位移场的影响规律。戚科骏等(2005)基于拉格朗日列式法，分析了压桩时产生的大变形，引入桩-土界面间的接触作用，并对桩周土体采用Mohr-Coulomb模型进行数值分析，得到了静力压桩过程中优化的数值模拟模型。计宏等(2009)用从初始半径a0的小孔扩张到2a0的过程来等效0～R的小孔扩张过程，将有限元分析运用到扩孔分析中，可对不同截面形状的桩进行扩孔分析，与圆孔扩张理论相比具有更好的灵活性和适应性。毕庆涛等(2011)通过在桩顶应用位移边界条件模拟了静压桩连续的贯入过程。同时，使用ALE方法对再次细分有限元计算网格以优化数据传输，获得了预制混凝土桩在砂土地基中的沉桩模拟过程，ALE法控制网格体积成形模拟过程(图8)。ALE有限元综合了拉格朗日有限元和欧拉有限元的优点。它通过对材料运动和网格运动分别进行描述，有效地控制了计算网格的变形，从而保证了网格的计算质量。可以看出，Lagrangian-Eulerian有限元技术和接触力学技术能够很好地应用于工程中的大变形与接触问题。曹明(2015)基于叠加原理，通过有限元法计算桩-桩位移相互作用系数，同时考虑了桩土分离后桩体孔洞的存在情况，减少了群桩的计算量，又提高了计算精度。

图7 有限元模型图(罗战友等，2005)

图8 ALE法控制网格扭曲(毕庆涛等，2011)

3.2 基于有限元软件的研究

随着有限元软件的普及，学者开始选择有限元软件对沉桩机理进行研究。ANSYS作为有限元分析软件在沉桩机理研究方面具有较好的适用性，该软件界面友好，操作简便，可以任意更改命令流方式来进行模拟计算，同时它的网格划分与结果后处理功能都很优异。许多学者使用ANSYS有限元软件对贯入机理进行研究：张明义等(2003a)基于有限元软件ANSYS对静压桩进行研究，提出位移贯入法，该法通过控制边界位移条件，考虑弹塑性本构关系等复杂问题，使桩体贯入的模拟更符合实际情况。鹿群等(2008)利用ANSYS和位移贯入法对静压桩的整个沉桩过程进行了模拟，并对静压桩在均质土和层状土中产生的位移应力场进行了详细的比较，经模拟获得了不同深度处的土体位移与应力。深度10im处的土体位移与应力曲线如图9，图10所示。

图9 土体位移(鹿群等，2008)

图10 水平挤压应力(鹿群等，2008)

但ANSYS有限元软件在土体本构模型选择方面有着较大的局限性。相比之下，有限元软件ABAQUS能够更好地满足多种土体本构模型的选择，模拟的静压沉桩过程更为准确可靠。因此许多学者选择通过ABAQUS有限元软件对贯入机理进行研究：寇海磊等(2012)基于ABAQUS软件模拟了层状土中静压桩的连续贯入，在原有模型的基础上优化了平滑桩的尖角与分层平衡地应力，其优化示意图如图11所示。同时设置了允许滑动的桩-土界面接触与约束、基于位移贯入法的边界条件设定等。获得了应力分布模拟结果，较为合理，实现了对静压桩的连续贯入的模拟。周小鹏等(2014)在ABAQUS中建立了渗透管桩模型，模拟了渗透与桩周土体固结过程，并利用圆孔扩张理论验证了模型，阐述渗透管桩贯入过程中位移场以及超静孔压场变化规律；对比分析静压桩和渗透管桩桩周土体固结性状，开拓了有限元软件的应用范围。桑松魁等(2018)运用有限元软件ABAQUS，在考虑土体弹塑性的本构关系、桩-土的接触类型以及土体初始应力的基础上，采用位移贯入法和Mohr-Coulomb准则，建立了静压桩贯入土体的有限元模型，实现了桩体位移的连续贯入，探讨了沉桩过程中桩周土的土中应力以及桩-土界面孔隙水压力随贯入深度的变化规律。肖昭然等(2019)采用有限元仿真软件ABAQUS建立了静压桩沉桩过程的3D模型，基于莫尔-库仑屈服准则，考虑到材料与位移的非线性和大变形，通过位移贯入法来模拟连续沉桩，得到了不同路径上的应力与位移变化图。

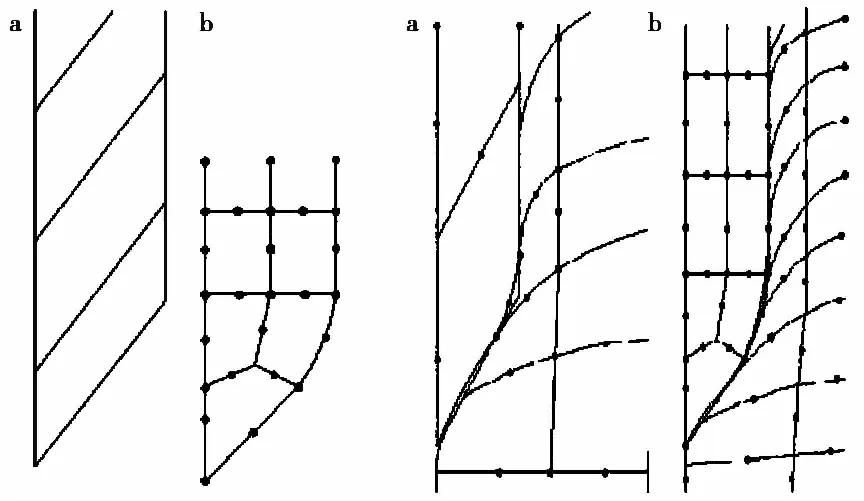
图11 模型单元划分与圆滑处理示意图(寇海磊等，2012)

通过ANSYS与ABAQUS的对比，可以看出两种有限元软件有着各自的优势与不足，两者的对比如表1所示。

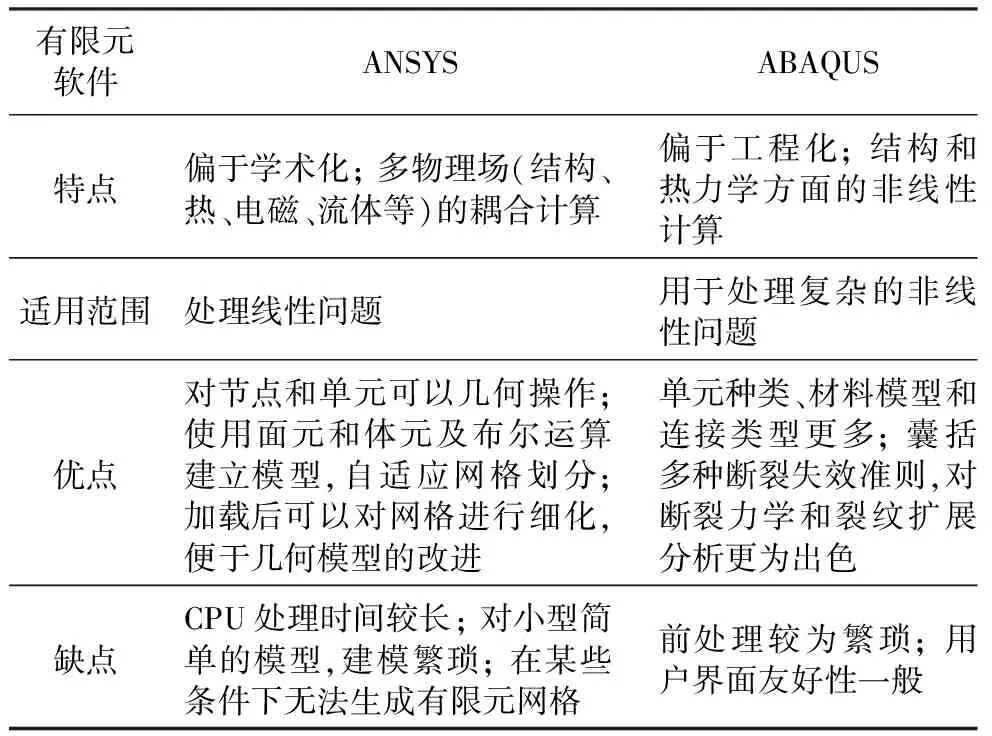
表1 有限元软件的对比

在理论分析方面，有限元方法在各类工程计算中应用较广，该法能将土体位移、应力、孔压等全面考虑。但在现有研究的基础上，有限元模拟仍存在以下问题：

(1)有限元计算的计算结果取决于本构模型的选取以及模型参数的设定。模型参数需要通过土工试验来获得，在目前的岩土工程试验中，样品的制备比较困难，模型参数的确定大多基于经验。

(2)对于静压桩的贯入过程难以进行准确的模拟，通过将有限元计算获得的沉桩过程与实际沉桩过程进行对比，可以发现，有限元软件对于沉桩贯入过程的模拟精度仍有待提高。

因此，对静压桩贯入过程的有限元模拟进行优化设计，如何将基于大变形理论有限元模拟成果应用于实际分析，为实际工程提供参考依据，具有较大的工程意义。

4 对静压桩贯入特性理论研究的展望

4.1 3种理论方法的对比

通过对各种理论研究方法的分析，静压桩沉桩机理研究的主要问题为：(1)沉桩贯入阻力的分布；(2)总径向应力沿水平方向的规律；(3)超孔隙水压力沿水平方向的规律。

通过表2的总结对比不难发现，3种理论方法各有利弊，同时也相辅相成。圆孔扩张理论作为目前应用最为广泛的理论研究方法，已成为理论研究的基石，其对研究沉桩过程中桩土界面的受力机制有着较高的适用性；应变路径法对于圆孔扩张理论起到补充作用，可以给出沉桩贯入过程中桩周土体的应力位移分布规律；而有限单元法的全面性使其在静压桩贯入机理理论研究中的应用越来越多，成为工程计算中获得土体应力位移的主要方法。

表2 理论方法对比

4.2 理论研究的展望

(1)在上述理论方法中，应变路径法过于繁复，鲜有学者通过此法进行研究；有限元模拟法的力学原理快捷高效，但在进行模型参数取值时，范围较广，难以获得确定值；圆孔扩张理论作为目前应用最为广泛的理论方法，其对于沉桩过程中土体的侧向挤压扩张研究有着较高的适用性，方法也较为简便；同时圆孔扩张理论存在一定缺点，圆孔扩张理论中未将深度方向的影响考虑在内，将空间球(柱)体的问题简化成平面上的应力-应变，该方法对于深度较小的情况适应性较好，但对于静压桩的贯入过程，简单地将z坐标方向的影响直接忽略，会导致理论与实际应用间存在偏差。故有必要从理论分析入手，基于圆孔扩张理论，加以有效修正，从土的非线性、桩与土的共同作用、空间特性等对静压桩的沉桩机理本质进行分析；而大变形问题的研究尚需深入。

模拟静压桩沉桩时，圆孔扩张理论为简化计算，通常认为是平面应变，也就是孔壁的内部压力沿深度方向是恒定的，孔壁的摩擦力忽略不计，土体中应力不受深度方向的影响。这种假定不仅未考虑上覆土重的问题，而且忽略了压力与摩擦力随深度的影响，得到的位移、应力均与深度无关。对于桩长相对较小时，深度方向的影响较小；但桩长超过20im后，深度方向的影响不可忽视。因此，基于空间理论分析静压桩贯入特性，有着重要的工程和理论价值。

首先基于圆孔扩张理论，建立确定应力边界条件的平衡微分方程；选择合适的应力函数，对弹性区的应力、位移、超孔压解析解进行推导，塑性区采用Mohr-Coulomb屈服准则进行求解，获得塑性区应力、位移、超孔压解析解。后续可通过实测数据验证上述方法的准确性，并通过有限元理论进行数值分析，对理论公式计算值、工程实测值和有限元计算值进行对比分析，进一步验证理论的正确性，得到更为准确合理的成果。