基于Floyd算法的裂隙岩质斜坡稳定性分析
2022-05-11兰志广陈润桥聂细江刘明亮
兰志广,陈润桥,聂细江,郭 猛,刘明亮
(天津市勘察设计院集团有限公司,天津 300191)
1 概述
裂隙岩质斜坡的稳定性多由赋存于坡体内的裂隙决定[1]。而由于裂隙的各向异性以及空间复杂性,针对裂隙岩质斜坡的稳定性研究仍十分困难。目前,针对裂隙岩质斜坡稳定性研究通常包括最危险滑动面的确定以及安全系数计算[2]。许多学者采用动态规划法或者智能算法来确定危险滑动面,并取得理想结果。如张文等[3-4]考虑裂隙的随机性,综合采用改进的随机动力学法、裂隙频率法以及Dijkstra最短路径算法确定了裂隙岩质斜坡的最危险滑动面;徐佩华等[5-6]考虑裂隙岩质斜坡的应力场特征,采用遗传算法确定了最危险滑动面;段荣福[7]采用不平衡推力法计算出每个可能剪出口的剩余下滑力,结合最优理论法确定了斜坡最危险滑动面。在确定最危险滑动面之后,就可以根据最危险滑动面上岩土体的抗剪强度参数来计算裂隙岩质斜坡的安全系数。此外,随计算机技术发展,裂隙岩质斜坡稳定性数值分析也取得迅速发展与广泛应用。如Grifiths,Nour等[8-9]利用有限元模型确定斜坡的最危险滑动面并计算出安全系数;韩建国[10]基于有限差分法,利用强度折减法对裂隙岩质斜坡稳定性及破坏模式进行了评价;程谦恭等[11]利用离散单元法模拟评价裂隙岩质斜坡稳定性。
尽管针对裂隙岩质斜坡的稳定性研究取得了许多成果,但综合考虑裂隙发育特征并合理确定裂隙岩质斜坡安全系数的方法仍然较少。本文提出了一种基于裂隙网络模拟技术及Floyd算法的裂隙岩质斜坡稳定性分析方法。该方法首先根据现场裂隙发育特征模拟生成主滑面二维裂隙网络,然后采用Floyd算法搜索不同剪入-剪出口之间的危险滑动面,最后利用传递系数法计算所搜索的危险滑动面的安全系数,以最小的安全系数作为对裂隙岩质斜坡整体稳定性的评估。
2 裂隙网络模拟
根据岩体结构控制论,岩体稳定性是由赋存于岩体内部的结构面控制的[12]。因此,在裂隙岩质斜坡稳定性分析前,首先要分析斜坡岩体内裂隙的特征信息。本研究方法是在二维尺度上分析评价裂隙岩质斜坡稳定性,首先要获得斜坡主滑面二维裂隙网络。在实践中,主滑面上的裂隙网络通常难以调查到,因此需要根据露头面裂隙信息模拟生成主滑面二维裂隙网络(见图1)。具体介绍如下。
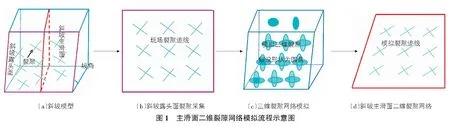
2.1 三维裂隙网络模拟
三维裂隙网络模拟技术是近半个世纪以来不断发展和完善用以表征岩体内部裂隙发育特征的最有效方法。该方法是基于现场实测裂隙数据,通过统计其迹长、产状、密度等参数的概率分布类型,采用Monte Carlo模拟生成与现场裂隙统计相似的数学模型[13]。
裂隙岩质斜坡岩体内部三维裂隙网络模拟主要步骤为:
1)裂隙位置模拟。
通常,采用泊松分布的方法在三维空间内生成裂隙几何中心的坐标点。
2)裂隙尺寸模拟。
迄今为止,裂隙形状尚未有统一定论,因此常假设裂隙形状为圆盘、多边形等。为简化建模程序,在工程实践中,常将裂隙形状假设为圆盘。基于裂隙形状为圆盘的假设,裂隙尺寸用圆盘直径表征。裂隙直径一般服从正态分布、对数正态分布以及伽马分布。
3)裂隙产状模拟。
裂隙产状通常服从Fisher分布、Bingham分布、双变量正态分布以及经验分布。
4)裂隙密度确定。
采用测线法可以获得裂隙间距,基于此,可推导出三维空间内裂隙密度。
5)Monte Carlo模拟。
采用Monte Carlo模拟对上述各项参数进行融合,即可生成与现场实测裂隙具有相似统计特征的三维裂隙网络模型。
2.2 主滑面二维裂隙网络生成
基于裂隙为圆盘的假设,并忽略裂隙的空隙及其起伏,那么决定裂隙圆盘位置、大小与形态的参数有圆盘中心点的坐标(xc,yc,zc)、圆盘直径D以及裂隙的倾向α与倾角β,以这些参数即可表达三维裂隙网络模型内的裂隙圆盘。选择主滑面与三维裂隙网络模型相截切,即可得到主滑面上的二维裂隙网络。具体地,主滑面二维裂隙网络数学模型表达式为:
(1)
其中,A=sinβcosα;B=sinαcosβ;C=cosβ;θ为斜坡主滑面走向;(x0,y0)为斜坡主滑面任一点在三维裂隙网络中的坐标。
3 基于Floyd算法搜索危险滑动面
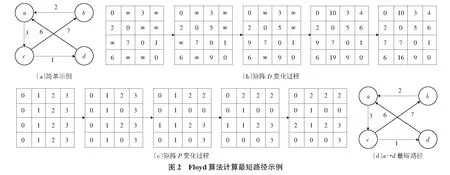
由于裂隙的强度参数相较岩石的强度参数小得多,因此在裂隙岩质斜坡滑动破坏时,滑动面往往沿着预先存在的裂隙扩展。斜坡滑动面经过的裂隙越多,抗滑力越小。当我们限定滑动面的剪入口与剪出口时,滑动路径的总长度越小,经过的裂隙长度越大,则沿着此路径滑动时所受的抗剪力越小。当滑动路径最短时,则最大可能的经过了岩体中的裂隙,沿此路径滑动时所受的抗剪力最小。由此分析可知,裂隙岩质斜坡危险滑动面的滑动主要沿剪入口与剪出口之间的最短路径。搜索最短路径的方法有很多种,由于Floyd算法容易理解,可以算出任意两个节点之间的最短距离且代码编写也很简单,因此我们采用Floyd算法搜索最短路径(即危险滑动面)。Floyd算法具体介绍如下:
通过Floyd算法计算各个节点之间的最短路径时,需要引入两个矩阵(矩阵D和矩阵P),矩阵D中的元素d[i][j]表示节点i(第i个节点)到节点j(第j个节点)之间的距离;矩阵P中的元素p[i][j]表示节点i到节点j经过了p[i][j]记录的值所表示的节点。假设有N个节点,则需要对矩阵D和矩阵P进行N次更新。初始时,矩阵D中节点d[i][j]的距离为节点i到节点j的权值;如果i和j不相邻,则d[i][j]=∞,矩阵P的值为节点p[i][j]的j值。接下来开始对矩阵D进行N次更新。第1次更新时,如果“d[i][j]的距离”> “d[i][0]+d[0][j]” (d[i][0]+d[0][j]表示i与j之间经过第1个节点的距离),则更新d[i][j]为“d[i][0]+d[0][j]”,更新p[i][j]=p[i][0]。同理,第k次更新时,如果“d[i][j]的距离”> “d[i][k-1]+d[k-1][j]”,则更新d[i][j]为“d[i][k-1]+d[k-1][j]”,p[i][j]=p[i][k-1]。更新N次之后,算法完成,结合矩阵D和矩阵P即可获得任意两节点的最短路径。
以图2所示节点为例,应用Floyd算法计算节点a与节点d之间的最短路径,通过更新矩阵D和矩阵P,可得到a→d之间的最短路径为a→c→d,最短距离为3+1=4。
由于Floyd算法针对节点进行搜索,故在实际搜索时,需将主滑面二维裂隙网络中的裂隙迹线进行离散化。裂隙迹线离散化程度越高,搜索结果越精确,但计算量也越大。此外,在实际搜索时,也需要预先对滑动面剪入口与剪出口进行设定。在实际斜坡滑动时,危险滑动面会优先选择剪入口与剪出口处发育的裂隙,故在实际搜索过程中,将二维裂隙网络的边界假设为裂隙。离散化程度随主滑面尺寸而定。
4 传递系数法计算安全系数
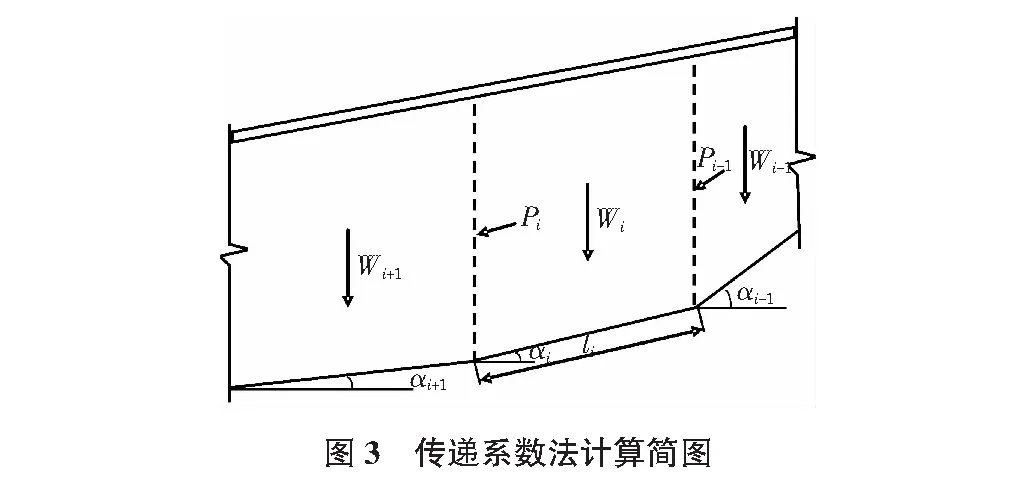
得到斜坡危险滑动面后,我们可以根据GB 50330—2013建筑边坡工程技术规范计算斜坡的安全系数。由于基于Floyd算法搜索所得的危险滑动面形态为折线形,故采用传递系数法进行斜坡安全系数计算。
根据传递系数法(见图3),斜坡安全系数(Fs)可按下列公式计算:
Ri=Wicosαitanφi+cili。
Ti=Wisinαi。
Ψj=cos(αi-αi+1)-sin(αi-αi+1)tanφi+1。
其中,Ri为第i计算条块单位宽度重力引起的抗滑力;Ti为第i计算条块单位宽度重力引起的下滑力;Ψj为第i计算条块对第i+1计算条块的传递系数;ci为第i计算条块滑面的黏聚力;φi为第i计算条块滑面的内摩擦角;li为第i计算条块滑面的长度;αi为第i计算条块滑面的倾角。
5 举例分析
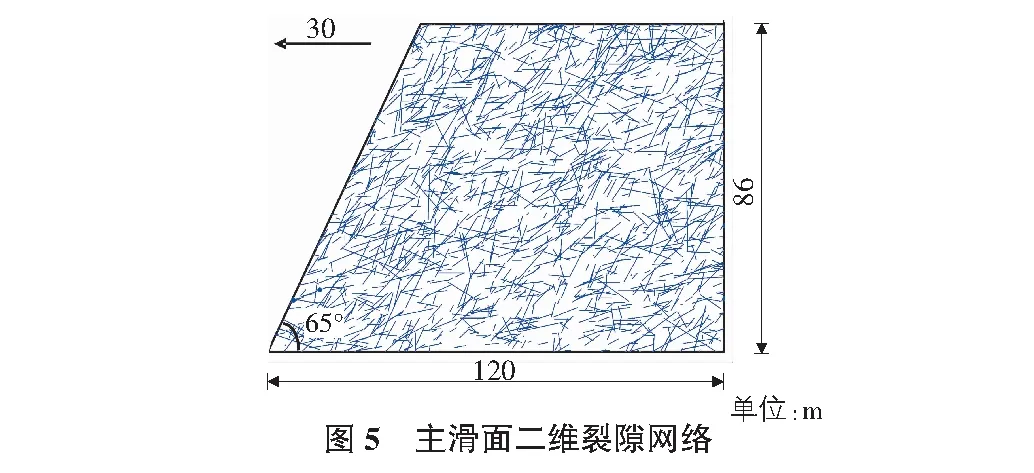
应用上述方法对某裂隙岩质斜坡进行稳定性分析。该裂隙岩质斜坡特征以陡峻地形为主,坡脚、坡顶地形相对高差86 m,斜坡坡面平均产状为30°∠65°。坡面多为基岩出露,岩性主要为闪长岩,表现为块状构造,主要成分为白色的斜长石和深色的角闪石。此外,长期受内外动力地质作用的影响,坡面岩体结构破碎,节理裂隙十分发育。
通过分析测量所得420条裂隙的迹长及产状信息,并采用动态聚类法进行分析,可将其划分为三个优势组,产状分别为150°∠71°,89°∠43°和339°∠42°。据此确定裂隙的概率分布类型,见表1。
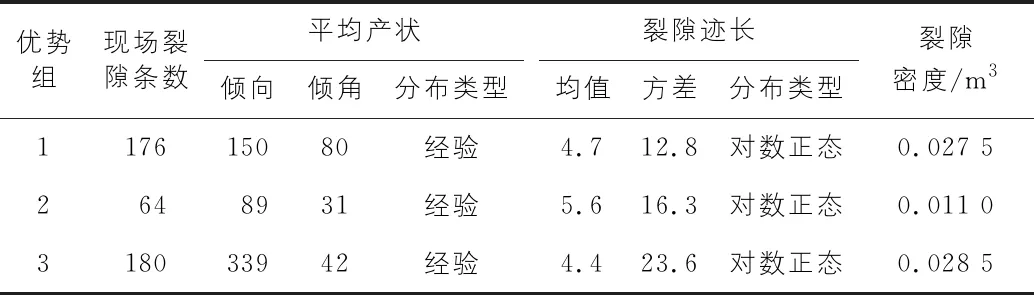
表1 裂隙优势组主要参数汇总
对现场取样岩石进行室内实验,确定岩石黏聚力为24.6 MPa、内摩擦角为53°、岩石密度为2.8 g/cm3;对于裂隙强度参数,由于现场裂隙基本闭合且无填充,故黏聚力为0,裂隙内摩擦角采用基本内摩擦角,参照Brideau[14]研究取值为27°。
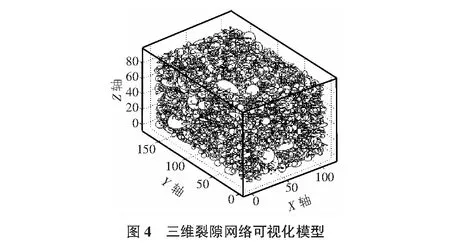
采用三维裂隙网络模拟技术,对该裂隙岩质斜坡岩体内裂隙进行模拟。最终,模拟一个尺寸为110 m(X轴)×170 m(Y轴)×90 m(Z轴)的三维裂隙网络,其可视化模型见图4。现场调查该裂隙岩质斜坡可能沿临空方向滑出,因此我们选取垂直于斜坡露头面走向的铅直平面为斜坡主滑面,并以此面截切三维裂隙网络得到该裂隙岩质斜坡主滑面的二维裂隙网络(见图5)。
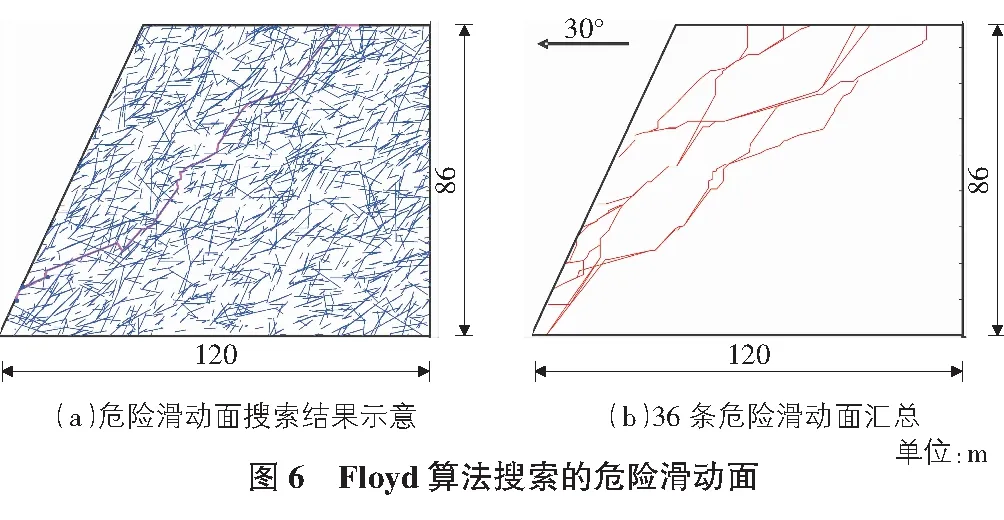
采用Floyd算法对该裂隙岩质斜坡进行危险滑动面搜索时,为保证搜索精度同时减少计算量,统一将主滑面二维裂隙网络中的每一条裂隙迹线离散成5个节点(4等分);将主滑面二维裂隙网络的边界每隔10 m设置一个节点。最终,选取剪入口(60 m,86 m),(70 m,86 m),(80 m,86 m),(90 m,86 m),(100 m,86 m),(110 m,86 m)与剪出口(0 m,0 m),(4.66 m,10 m),(9.32 m,20 m),(13.99 m,30 m),(18.65 m,40 m),(23.32 m,50 m)进行分析。组合任一个剪入与剪出口,采用Floyd算法即可获得36条危险滑动面(见图6)。
根据GB 50330—2013建筑边坡工程技术规范,采用传递系数法对获得的36条危险滑动面进行天然状态下安全系数计算,结果如表2所示。
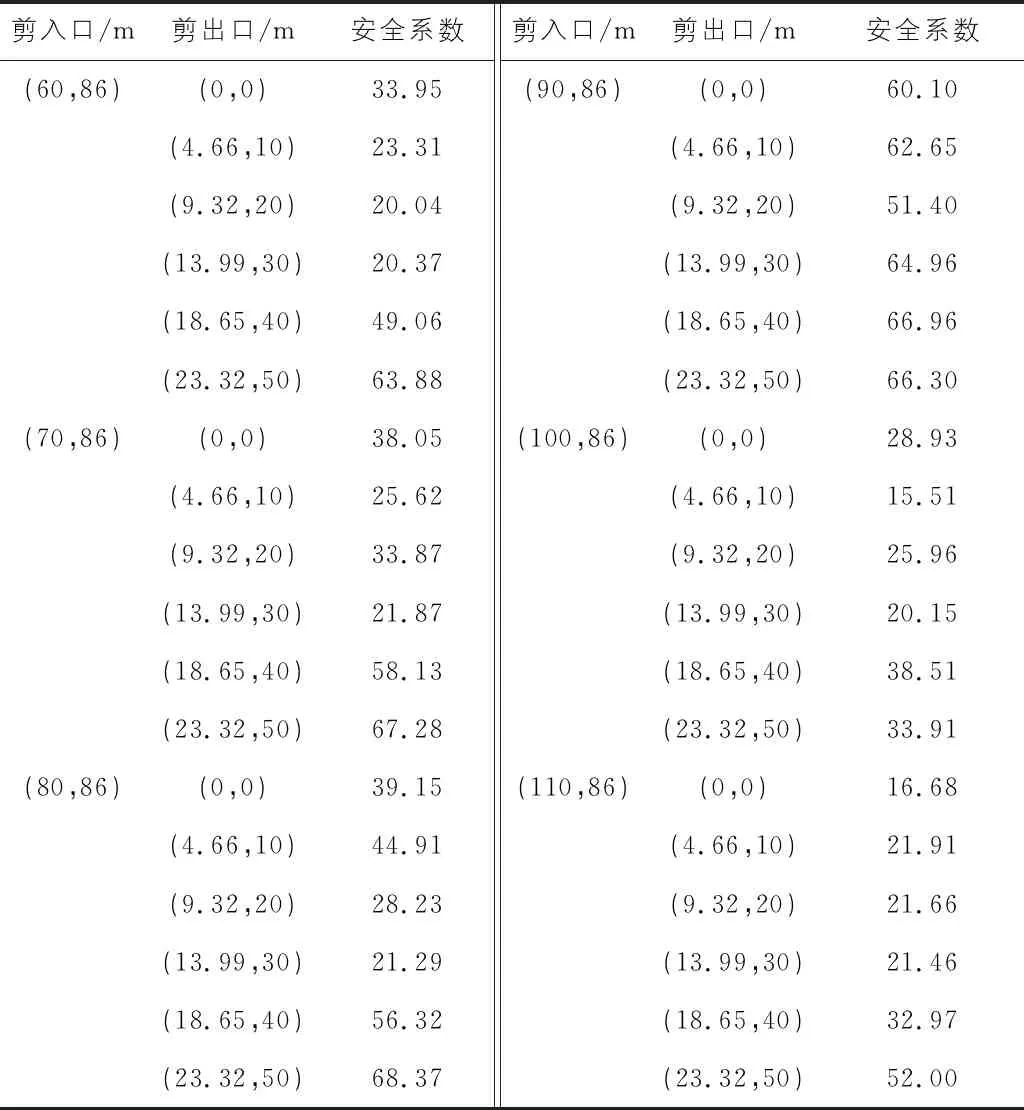
表2 各危险滑动面安全系数计算结果统计
由表2可知,不同剪入-剪出口组合之间危险滑动面所对应的安全系数不同。该裂隙岩质斜坡各危险滑动面最小安全系数为15.51,最大为68.37,均值为39.33。为保证工程安全性,选择最小的安全系数作为对整个裂隙岩质斜坡稳定性的评估,则该裂隙岩质斜坡安全系数为15.51,故天然状态下该裂隙岩质斜坡整体稳定性好。
6 结论
通过本研究提出的方法,针对某裂隙岩质斜坡进行研究,最终可得到以下结论:
1)裂隙岩质斜坡危险滑动面往往沿着预先存在的裂隙扩展,因此裂隙岩质斜坡稳定性分析前必须考虑斜坡主滑面裂隙的发育特征。由于斜坡主滑面裂隙网络在发生破坏前不可见,因而根据现场露头面裂隙信息模拟生成与现场裂隙统计相似的数学地质模型的裂隙网络模拟技术是裂隙岩质斜坡稳定性分析必不可缺的。
2)经分析,裂隙岩质斜坡危险滑动面的滑动主要沿剪入口与剪出口之间的最短路径。因而可视剪入口与剪出口之间的最短路径为裂隙岩质斜坡的危险滑动面。Floyd算法可以简单快速计算出任意两个节点之间的最短路径,因而能很好地被应用于裂隙岩质斜坡危险滑动面的搜索。
3)Floyd算法搜索得到的危险滑动面为折线形,因而可以采用传递系数法进行安全系数计算。不同危险滑动面对应的安全系数不同,选择最小的安全系数对整个裂隙岩质斜坡稳定性进行评估。对于研究案例,天然状态下安全系数为15.51,表明天然状态下该裂隙岩质斜坡整体稳定性好。
4)本文研究案例仅针对选定剪入-剪出口组合进行危险滑动面搜索,计算所得最小安全系数与实际可能存在一定误差,这个误差可通过增密剪入-剪出口组合来消除或缓解。
