基于三段式Halbach阵列的同轴磁性联轴器优化设计
2022-05-11秦清海汲柏良
秦清海,汲柏良
(曲阜师范大学 工学院,日照 276800)
0 引 言
传统的联轴器存在对中问题,若对中不良,将导致振动与噪声过大、转轴弯曲以及轴承磨损等一系列故障,严重降低设备的可靠性,增加维修费用。为提高联轴器的可靠性,有学者提出了一种基于磁力传动的磁性联轴器。由于该新型磁性联轴器具有物理隔离性好、无机械接触、可过载保护以及可靠性高的优势,已成功应用于石油化工、半导体、生物医药等行业[1-2]。常见的磁性联轴器有两种,分别是同轴磁性联轴器和平面磁性联轴器。
在磁性联轴器的理论分析与优化设计方面,许多学者进行了研究。文献[3]介绍了同轴磁性联轴器的结构特点并分析了影响其最大静态转矩的因素。文献[4]针对磁力泵联轴器推导出其由于端部漏磁损失的转矩值,为样机的研制过程提供了参考。文献[5]将一种两段式 Halbach永磁阵列应用于同轴磁性联轴器,在同等条件下Halbach阵列磁性联轴器的最大静态转矩提高了23.8%。理论证明该结构的磁性联轴器无需轭铁,可有效减小转动部件的转动惯量,缩短启动时间。文献[6]等推导了一种理想径向Halbach转子磁性联轴器的三维解析转矩方程,得出了峰值转矩的产生条件。
有限元方法可有效应用于复杂电磁场问题的求解,但随着网格剖分精度的提高,会出现计算效率低的问题。有限元方法和其它优化算法结合,用于各种电机拓扑的优化设计,是当下研究的热点。文献[7]将响应曲面法与遗传算法相结合对微型电动车驱动电机的成本进行了优化。文献[8]提出了基于自适应网格的有限元方法,采用多目标遗传算法对不同类型的电机拓扑进行了优化。文献[9]基于多目标粒子群算法对一台永磁同步电机的效率、功率因数以及起动性能进行了优化。
本文将一种三段式Halbach阵列应用于同轴磁性联轴器中,利用响应曲面法建立了永磁体转矩密度与磁性联轴器总体积的复合性能函数,并基于模拟退火(以下简称SA)算法对最优复合性能函数进行求解,得到了最佳的设计参数组合。仿真结果表明,优化后磁性联轴器永磁体的转矩密度得到了较大幅度的提升,磁性联轴器的总体积有所减小,验证了本文优化方案的有效性。
1 三段式Halbach阵列
传统的同轴磁性联轴器主要由内、外转子磁齿轮以及固定于其表面的永磁体组成,其中永磁体采用径向充磁方式,即N,S极交替排列的形式。图1给出了同轴磁性联轴器的拓扑结构以及重要尺寸标注。本文以一台功率等级为10 kW的同轴磁性联轴器为例进行说明,其技术指标如表1所示。其中,外转子磁齿轮、内转子磁齿轮分别作为主动轴与从动轴,外转子永磁体生成的旋转磁场与内转子永磁体生成的磁场相互作用,驱动内转子与外转子同方向旋转。为应对过载等不同工况,设定过载倍数为1.5,则该设计的最大静态转矩为286.5 N·m。

图1 同轴磁性联轴器的拓扑结构及相关参数

表1 10 kW同轴磁性联轴器的技术指标
Halbach阵列是一种新型的永磁体排列方式,它通过将充磁方向不同的永磁体按照一定顺序排列,可使气隙侧的磁场强度增强,达到节省永磁体材料、提高转矩密度的目的。本文采用的三段式Halbach阵列如图2所示。其中每个磁极都由一块径向充磁和两块充磁角度与其成45°的永磁体组成。
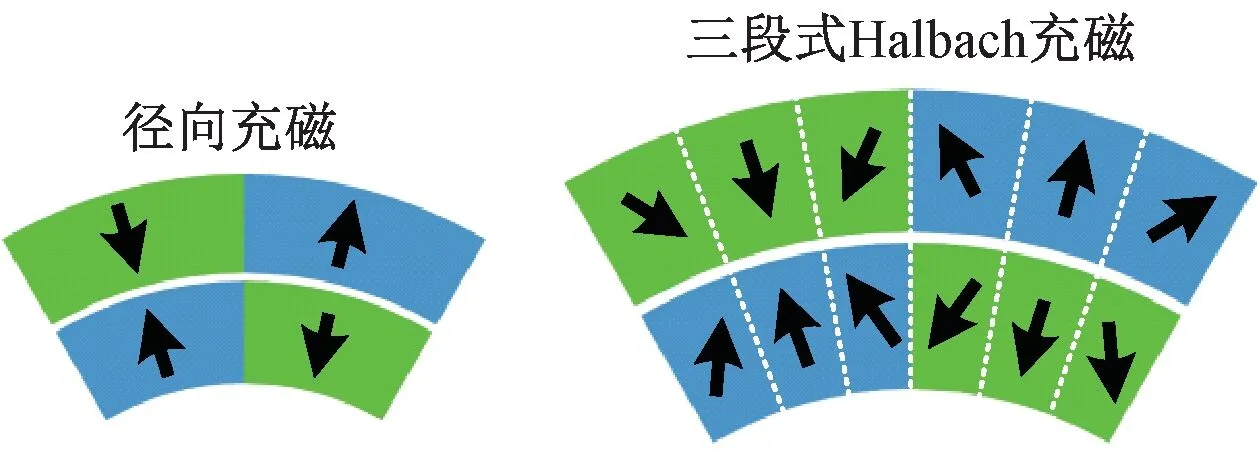
图2 径向充磁及三段式Halbach阵列
下面对采用Halbach阵列以及传统的径向充磁方式的同轴磁性联轴器性能进行了比较。根据有限元仿真实验,首先确定满足设计要求下使用径向充磁方式的技术指标各参数的初始值,如表2所示。保持表2中参数不变,将充磁方式改为Halbach阵列,采用两种不同充磁方式的磁性联轴器的磁力线分布对比如图3所示。可以看出,采用三段式Halbach阵列后,内外转子铁心部分磁力线大部分集中在气隙侧,气隙侧的磁感应强度得到了加强,永磁体的利用率得到了显著提高。

表2 各参数的初始值

图3 两种充磁方式磁力线分布对比
图4和图5分别给出了两种充磁方式下的气隙磁密与其傅里叶分解的谐波对比图。
由图4可以看出,采用三段式Halbach阵列之后气隙的径向磁密与切向磁密幅值均有所上升,并且径向磁密与切向磁密波形都具有8个波峰,这也说明了内外转子的磁极对数为8。

图4 两种充磁方式气隙磁密波形对比
由图5可以看出,两种充磁方式下的气隙磁密的谐波分量主要集中在基波(8对极)及其奇数倍谐波,而偶数次谐波含量很低。采用Halbach阵列后,径向谐波分量中除基波分量外,3次(24对极)、7次(56对极)、9次(72对极)以及13次(104对极)谐波幅值也有所增加。而切向谐波分量中除基波分量外,7次(56对极)、13次(104对极)谐波幅值增加较为明显。
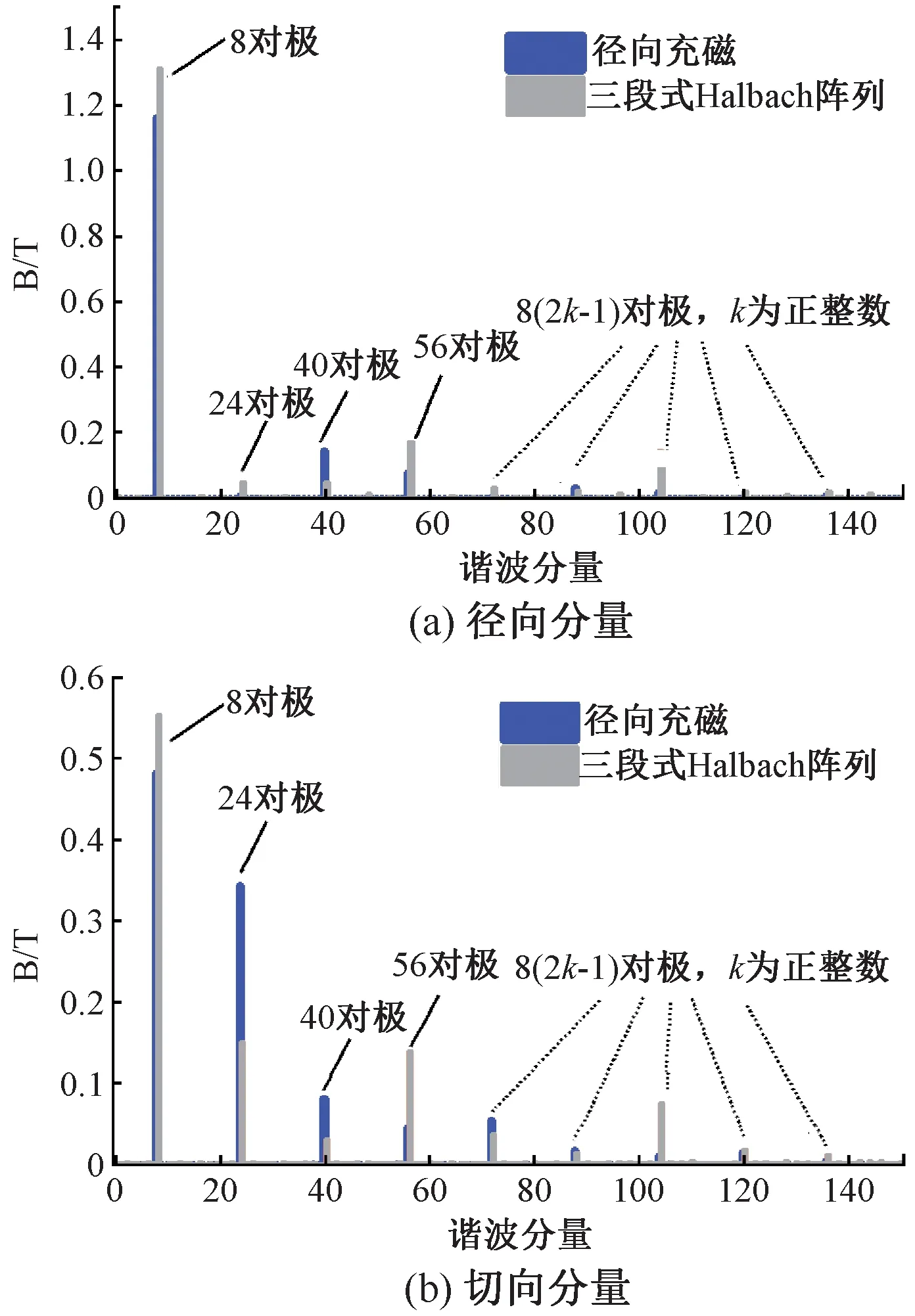
图5 两种充磁方式气隙磁场谐波对比
为定量研究三段式Halbach阵列对气隙磁密的影响,表3给出了两种充磁方式下幅值最高的前5组谐波径向与切向分量的幅值。

表3 两种充磁方式下各次谐波分量径向/切向磁密幅值
正弦波的波形质量通常用谐波畸变率THD衡量,其表达式:
(1)
式中:Bi为气隙磁密的各次谐波幅值;B1为气隙磁密的基波幅值。
由图5可以看出,前9次谐波已经占据了谐波含量的绝大部分。由式(1)可计算两种充磁方式下前9次谐波的径向与切向分量的谐波畸变率。经过计算,采用三段式Halbach阵列之后,径向分量的谐波畸变率由12.35%降低为5.27%,切向分量的谐波畸变率由73.24%降低为27.72%。这说明采用三段式Halbach阵列可有效提升气隙磁密波形的正弦性。
磁场耦合在内转子上产生的磁力转矩可由麦克斯韦张量法求得[10]:
(2)
式中:μ0为真空磁导率;Lef为联轴器的轴向长度;Rδ为气隙半径;Br、Bt分别为气隙磁密的径向与切向分量;θ为观测点所对应的极角。
图6给出了采用径向充磁与三段式Halbach阵列的联轴器内转子静态转矩波形。可以看出,在相同的尺寸参数下,采用径向充磁方式的内转子最大静态转矩为286.5 N·m,而采用三段式Halbach阵列后最大静态转矩达到了369.7 N·m,提升了接近29%,说明采用三段式Halbach阵列可有效提升同轴磁性联轴器的转矩密度。

图6 两种充磁方式静态转矩对比
2 优化参数与优化目标选取
针对同轴磁性联轴器的性能要求,一方面应在保证转矩性能达到要求的前提下尽量减少永磁体用量,提高其转矩密度、降低成本;二是受应用场景的限制,其总体体积不能过大,应设法提高其空间利用率。为此,选取磁性联轴器永磁体的转矩密度D以及磁性联轴器的总体积V作为待优化目标。
永磁体转矩密度D的计算公式如下:
(3)
式中:Tin为同轴磁性联轴器内转子的最大静态转矩;VPM_in、VPM_out分别表示内、外转子永磁体的体积,其计算公式如下:
VPM_in=πLef[(Rc-bout-hout-δ)2-
(Rc-bout-hout-δ-hin)2]
(4)
VPM_out=πLef[(Rc-bout)2-(Rc-bout-hout)2]
(5)
式中:Rc、Lef分别为同轴磁性联轴器的外转子半径与轴向长度;hin、hout分别内外转子的永磁体厚度;bin、bout分别内外转子的铁心厚度;δ为气隙长度。
同轴磁性联轴器总体积V的计算公式如下:
(6)
最终选取待优化的设计变量为同轴磁性联轴器外转子半径Rc、轴向长度Lef以及内、外转子永磁体的厚度hin、hout。
其次,采用三段式Halbach阵列后,为达到相同的转矩性能,对表2中的数值进行了初步优化,如表4所示。可以看出,在相同的转矩性能下采用三段式Halbach阵列之后,同轴磁性联轴器的轴向长度由90 mm减少为80 mm,永磁体厚度由5 mm减少为4.5 mm,通过进一步计算,永磁体的用量由0.313 8 dm3减少为0.243 7 dm3,减少了22.3%。

表4 各参数的初步优化值
3 基于响应曲面法的复合性能函数建模
响应曲面法(以下简称RSM)是一种基于数理统计的优化方法,它通过合理的实验设计以及较少的实验次数来获取较多的有效信息,RSM被广泛应用于机电设备的优化设计中[11-13]。
RSM实验样本数由下式确定:
N=2m+2m+1
(7)
式中:m=4为待优化的设计变量个数,N=25为RSM实验样本数。
基于表2中各参数的初始值,使用有限元软件ANSYS进行RSM实验,建立各优化目标与待优化的设计变量之间的二次回归(以下简称QR)模型:
(8)
式中:f1(x)、f2(x)为目标函数,分别表示永磁体的转矩密度D、同轴磁性联轴器总体积V的倒数的预测值;x为由待设计变量组成的设计向量,即:x= [x1,x2,x3,x4]= [Rc,Lef,hin,hout];α0、αm、αmn、β0、βm、βmn为回归系数;κ1、κ2为随机误差。
图7给出了设计变量关于转矩密度D的响应结果。

图7 各设计变量关于转矩密度D的响应结果
图8给出了使用RSM与QR方法得出的永磁体转矩密度D与同轴磁性联轴器总体积倒数V-1的对比图。判定系数R2定义为回归变量的回归平方和与总离差平方和的比值,其数值越接近1说明回归精度越高。经过计算,两者的判定系数分别为0.993 6与0.999 6,均高于0.99,说明回归精度较高,结果较理想。
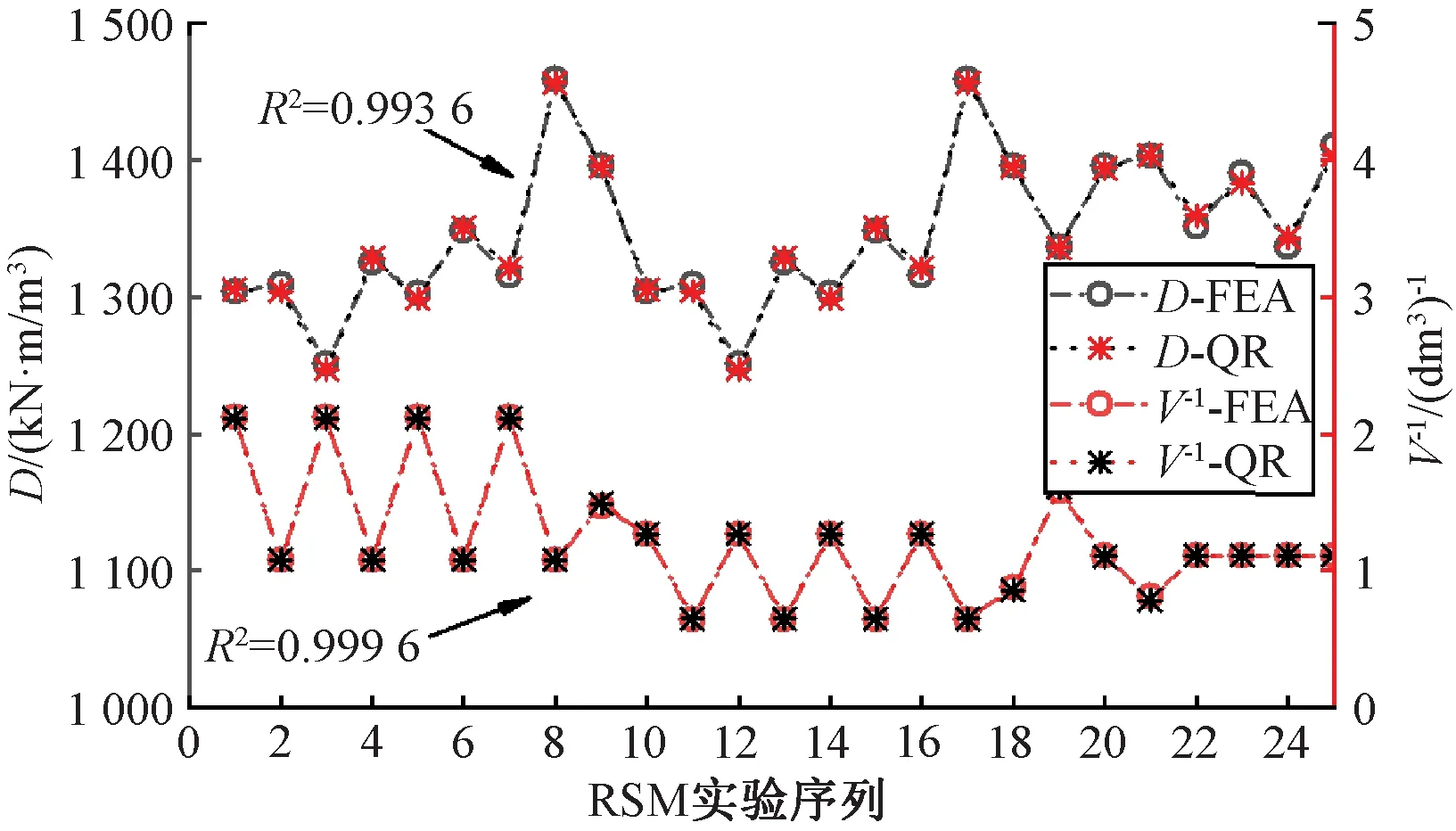
图8 拟合结果对比
引入复合性能函数F(x),根据图7的实验结果确定各设计参数的取值范围,将研究问题转化为下式的单目标非线性规划问题:
maxF(x)=max[w1γ1f1(x)+w2γ2f2(x)+
λΦ-1(x,Tin0)]

(9)
式中:F(x)为复合性能函数,它综合考虑了设计变量对各性能指标的影响;w1、w2表示权重系数,且有w1+w2=1;γ1;γ2表示尺度系数,用于平衡不同性能指标之间量纲与量级的差异性;λΦ-1(x,Tin0)为惩罚项,用于将含函数约束(即目标转矩约束)的优化问题转化为无函数约束最优化问题;λ为惩罚因子;Φ-1(x,Tin0)为惩罚函数,其表达式如下:
(10)
式中:f3为内转子最大静态转矩的预测值,其形式与式(8)中f1、f2的形式一致;Tin0为内转子最大静态转矩的目标值,此处取值为286.5 N·m。
尺度系数γ1、γ2的计算公式如下式:
(11)
(12)
式中:Dmax、Dmin分别表示RSM实验中永磁体转矩密度D的最大值、最小值;Vmax、Vmin分别表示RSM实验中同轴磁性联轴器总体积V的最大值、最小值。
由于优化目标永磁体转矩密度拟合结果的判定系数低于总体体积的倒数,因此给予前者较小的权重系数值,以降低回归精度较低带来的误差,表5给出了权重系数与尺度系数的取值。

表5 权重系数与尺度系数的取值
4 SA算法寻优
SA算法相对于传统的优化算法能够以一定的概率接受比当前解要差的解,因此有较大可能性跳出局部最优解,达到全局最优解。且该法计算过程简单、鲁棒性强,可用于复杂非线性规划问题的求解[14-15]。由于SA算法擅长无函数约束的目标优化问题,故在式(9)中引入了惩罚函数项,将其转化为无函数约束的优化问题。设置迭代次数为1 000次,适应度函数取为-F(x),惩罚因子λ=0.01,使用SA算法对式(9)进行求解。图9给出了当前适应度函数与最优适应度函数的优化迭代过程。可以看出,在第500代时,适应度函数就已经收敛,最终的适应度函数为-2 832.65。

图9 适应度函数的优化迭代过程
本文的同轴磁性联轴器的优化设计流程图如图10所示。

图10 本文优化设计流程图
表6给出了使用SA算法优化前后各参数的值,其中值3为优化后各参数的值。可以看出,采用三段式Halbach阵列的联轴器经优化后,内、外转子永磁体厚度有所增加,但轴向长度由80 mm减小为74.83 mm。
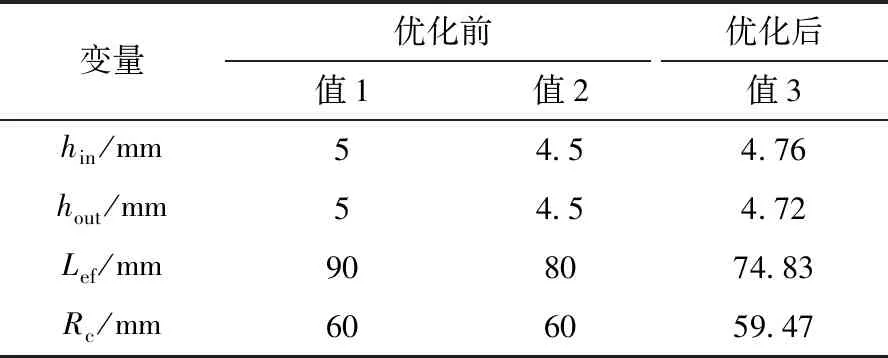
表6 各参数优化前后对比

图11 优化后磁性联轴器各性能指标对比
图11对图10的设计流程各性能指标优化前后进行了比较。可以看出,永磁体转矩密度由1 395.4 kN·m/m3提升至1 405.1 kN·m/m3,总体积由0.905 dm3减小为0.831 dm3,减小了8.2%。相对于原始的径向充磁方式,优化后的永磁体转矩密度提升了53.9%,联轴器的总体积减小了18.4%。其中,永磁体转矩密度大幅提升的主要原因是采用了三段式Halbach阵列。
图12给出了优化前后同轴磁性联轴器的3D模型图。可以看出,优化后联轴器的总体积和永磁体用量均有所减小,降低了成本、提高了空间利用率。

图12 优化前后磁性联轴器3D模型对比
图13与图14分别给出了优化后联轴器的磁场强度分布云图以及磁力线分布图。可以看出,磁力线分布合理,漏磁较少,铁心材料得到了充分利用。这充分说明了三段式Halbach阵列以及优化策略的有效性。

图13 优化后的磁场强度分布云图

图14 优化后的磁力线分布图
图15给出了优化前后磁性联轴器内转子的静态转矩波形对比。可以看出,优化前后最大静态转矩变化不大,满足设计转矩为289.5 N·m的要求。
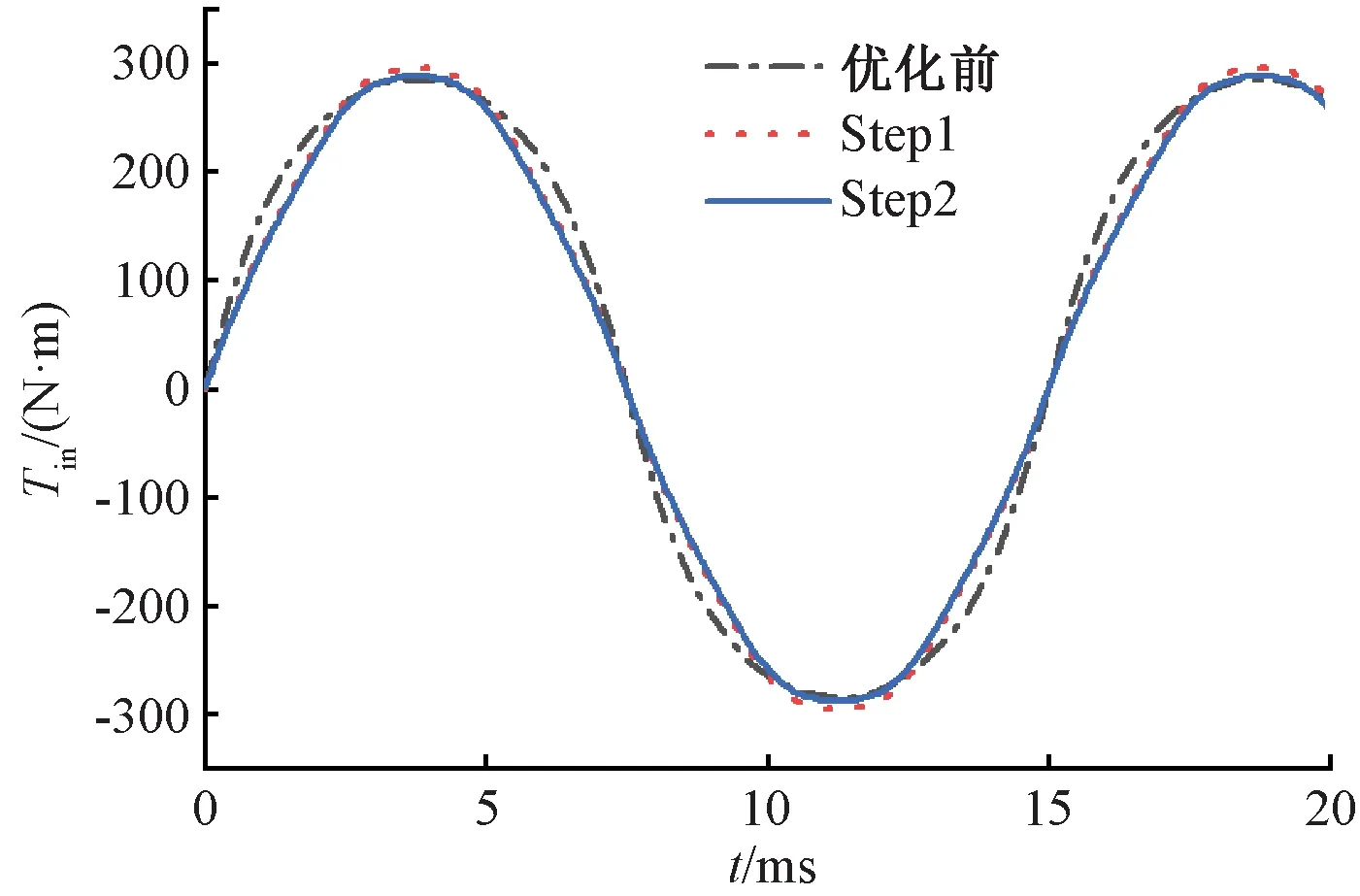
图15 优化前后内转子静态转矩对比
5 结 语
通过仿真实验验证与分析可以得出如下结论:
(1)采用三段式Halbach阵列可显著提升同轴磁性联轴器的转矩密度,有效减少其总体积;
(2)以永磁体的转矩密度以及同轴磁性联轴器的体积为优化目标,合理选取优化变量,采用响应曲面法与模拟退火算法相结合的优化策略对复合性能函数进行求解,可起到提高空间利用率、节省永磁材料的目的,同时提高了实验效率。
