基于流固耦合的喷水推进泵叶轮不平衡振动特性分析

熊文， 徐增丙， 王名扬

(1.喷水推进技术重点实验室， 上海 200011；2.武汉科技大学， 冶金装备及其控制教育部重点实验室， 湖北， 武汉 430081)

0 引言

喷水推进泵通过喷射水流产生的反作用力推动船体快速前行而广泛用于现代高速船上[1-2]。随着喷水推进泵容量不断提升，喷泵的结构尺寸、工况参数等不断增大，喷泵振动问题也更为突出。

泵的振动主要分为水力振动和机械振动，非稳态流体激振力和转子不平衡则分别是2种振动形式的主要诱因[3-4]。其中，水力振动是喷泵设计的主要考虑因素，目前已开展了大量的研究，如:窦唯等[5]对高速泵三维流场进行了非定常计算，分析了高速泵内的压力分布情况，得到了流体激振力对高速泵叶轮系统的振动及其轴心轨迹的影响；何涛等[6]建立了适用于离心泵等叶轮机械流动诱发振动的数值模型，分析了泵流场、振动激励源和振动响应等特性；司乔瑞等[7]采用单向流固耦合方法对叶轮转子系统进行瞬态动力学计算，分析了带诱导轮高速离心泵的流动诱导振动特性；赵博等[8]通过有限元分析软件对某台立式轴流泵内流体压力脉动引发的结构振动响应进行了仿真计算；高丹妮等[9]分析了流体激励下结构的振动位移响应和辐射声场分布，但这些研究均只是单纯从流体激励力方面对泵的振动特性进行了分析。泵机械振动的分析尤其是考虑非稳态流体激振力和不平衡质量等多重因素的也鲜有研究，如:邹奋[10]分析了流体激励力和转子不平衡力作用下钠泵振动响应；姚永灵等[4]建立了泵转子有限元模型，研究了不平衡质量与非稳态流体激振力对转子振动特性对的影响，但考虑到计算复杂性这些研究对泵转子模型进行了简化分析，影响了计算精度，并且目前对喷水推进泵的机械振动分析也寥寥无几。

本文针对喷水推进泵在长期运转中叶轮磨损、腐蚀或黏渣等原因造成叶轮质量不平衡的问题，以1台混流式喷水推进泵为研究对象，采用单向耦合的方法，对喷水推进泵转子在不平衡质量力与非稳态流体激励力下的振动特性进行分析。

1 计算模型

1.1 流场计算模型

建立混流式喷水推进泵及流道三维模型如图1所示。其中叶片数Z1=6片、导叶叶片数Z2=11片，并且为保障进出水流的均匀性，用直管代替了进水弯管，并对泵的进出口段长度进行了适当延伸。计算分析时设定流量Q=2.53 m3/s、扬程H=25.6 m、转速n=1 000 r/min、转频f=16.6 Hz,叶轮通频fn=100 Hz。

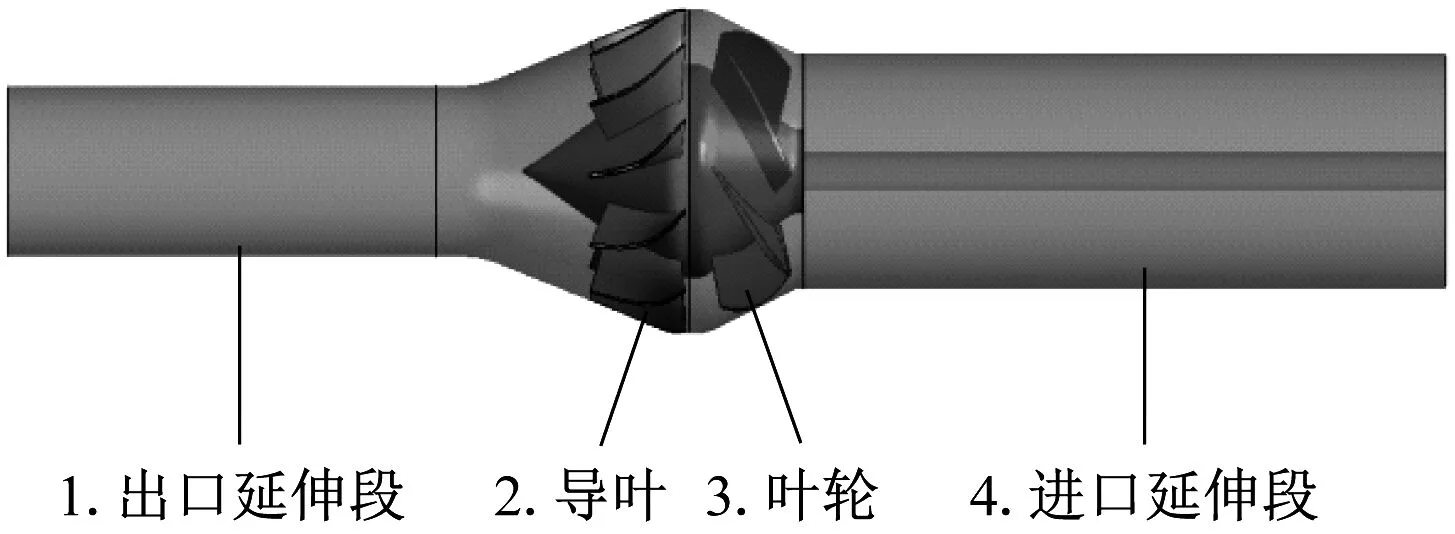
图1 喷水推进泵数值计算域

1.2 振动计算模型

混流式喷水推进泵主要由泵壳及转子系统组成。为了节约计算资源，只对转子系统做单向流固耦合分析。推进泵转子三维模型如图2所示，考虑到实际监测时只能在轴承处布置测点，故在叶轮的左、中、右轴承处提取振动响应信号，即监测点为图2中的P1、P2、P3处。

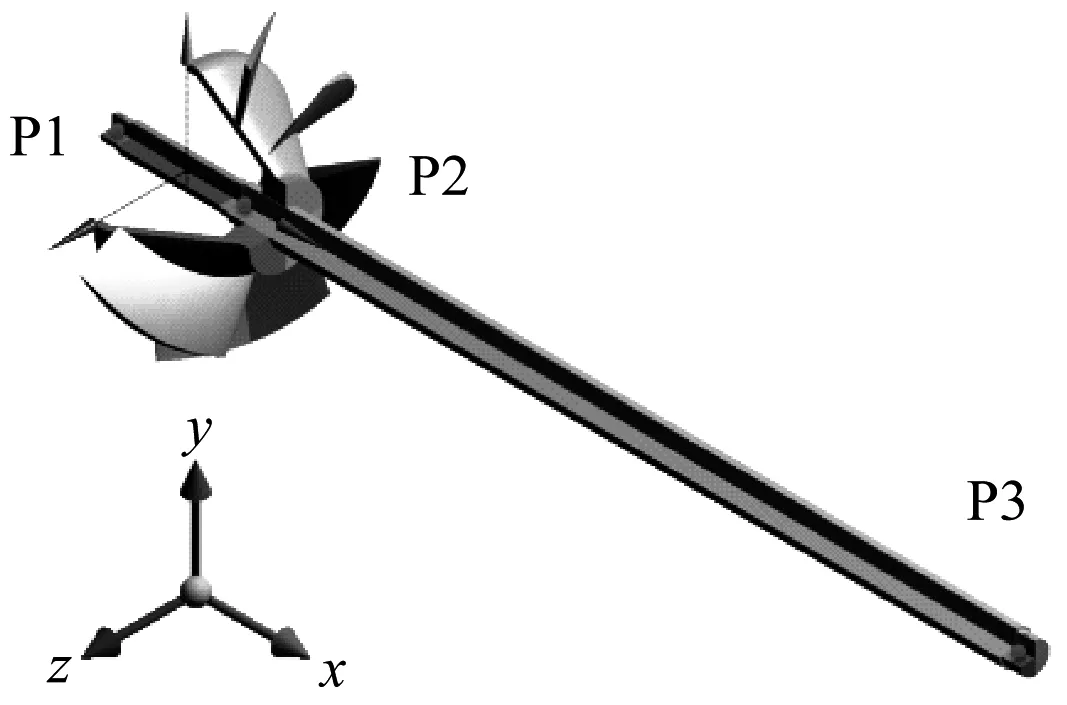
图2 混流式喷水推进泵叶轮转子模型

2 数值计算方法

2.1 流场计算分析

对混流式喷水推进泵数值计算区域进行非结构网格划分，并对流动剧烈变化的区域如叶轮及导叶部分进行适当网格加密如图3所示，网格总数约250万。通过网格的独立性验证分析,网格数大于250万时混流式喷水推进泵的扬程和效率受网格的变化影响较少。

(a) 导叶

在计算分析过程中，选取SST湍流模型，设定收敛精度为10-5s。进出口边界条件分别设定为质量流量进口和静压出口，壁面采用无滑移边界条件，并将稳态数值计算的结果作为瞬态数值计算的初始条件，以期提高收敛速度及计算稳定性。并且，当叶轮转速为1 000 r/min时，时间步长设定为0.000 5 s，即每个时间步长内叶轮旋转3°，故其旋转1周需120步，采样时间共0.36 s即6个旋转周期。

2.2 振动计算分析

混流式喷水推进泵转子部分选用双向不锈钢材料，其物性参数如表1所示。

表1 转子材料物性参数

采用单向流固耦合的方式对推进泵转子振动响应进行计算，结构域计算在瞬态分析模块中进行，结构域的边界条件与实际相匹配，其边界条件如图4所示。轴承采用弹簧单元代替，在轴肩位置设置位移约束限制轴向窜动。叶轮转子的质量不平衡采用不平衡力模拟。

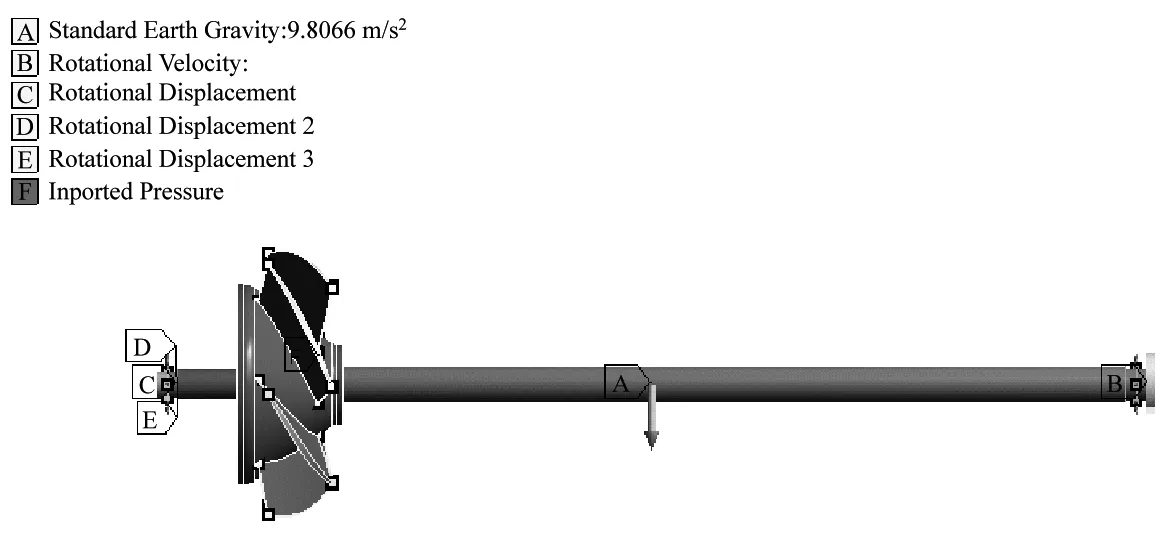
图4 叶轮转子的载荷与约束

本文主要分析喷水推进泵在非稳态流体激振力及叶轮不平衡质量力的作用下叶轮转子的振动响应特性，计算分析时，利用流场计算获取作用于叶轮转子上的非稳态流体激振力，而叶轮不平衡质量力则通过在瞬态分析过程中加载正余弦载荷的方式进行模拟计算。设置时间步长及总时间与流体计算保持一致分别为0.000 5 s和0.36 s。

3 计算结果分析

3.1 流场计算结果

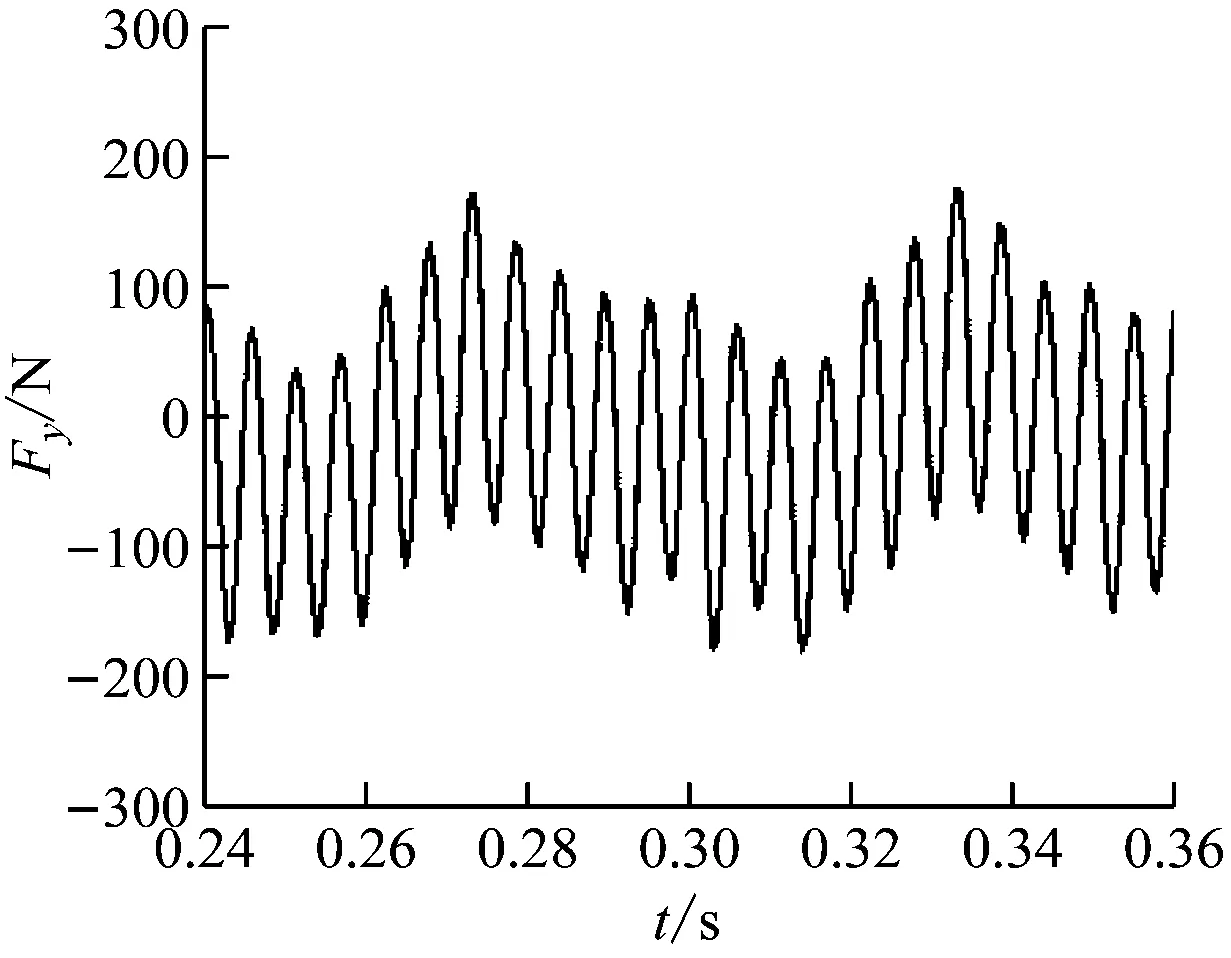
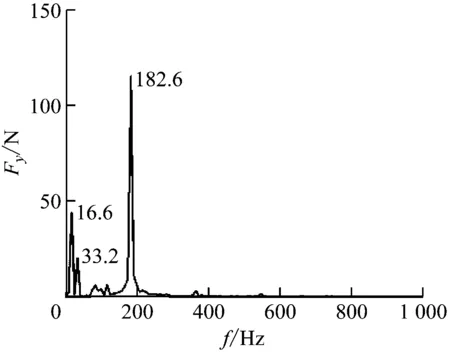
对混流式喷水推进泵的非定常流动分析中，径向力的大小影响着叶轮转子的振动响应。叶轮周围流场压力分布不均匀是导致叶轮产生径向力的主要原因。图5、图6分别给出了转速为1 000 r/min时叶轮所受到的流体径向力时域和频域图。图5为叶轮旋转最后2个周期时Y向和Z向上非稳态流体激振力时域图，从图中可以看出两方向上的非稳态流体激振力均表现出了良好的周期性，但Y向波动幅度要略大于Z向。图6为非稳态流体激振力频域图，从图中可以看出，Y向和Z向流体激振力均具有多种频率成分且基本一致，其中幅值最大的是11倍频，刚好对应导叶叶片数，其次是1倍频，最后是2倍频。

3.2 叶轮振动响应分析

3.2.1 流体诱导的振动响应分析

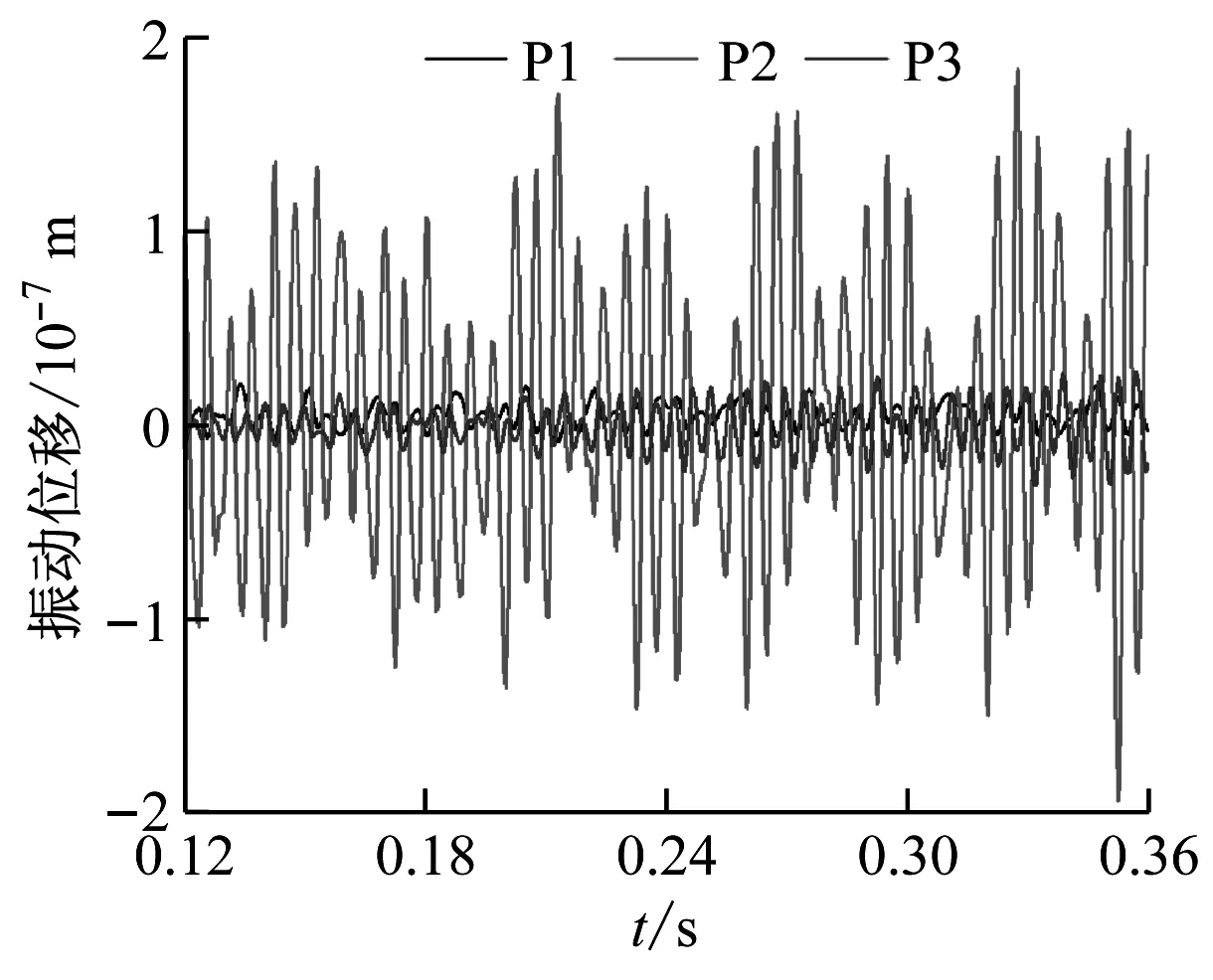
仅考虑非稳态流体激振力时叶轮转子各轴承监测点处的振动响应如图7(a)所示，从图中可以看出各轴承点处的振动位移信号呈周期变化，且中间轴承P2处的振动最大，其次是右端轴承P3处的振动，而左端轴承P1处的振动最小；相应地各轴承处振动位移信号的频谱如图7(b)所示，从图中可以看出中间轴承P2点处振动信号的主频为轴频的11倍，次频为1倍频。

(a) Y方向

(a) Y方向

(a) 时域

3.2.3 叶轮不平衡及流体诱导的叶轮振动分析

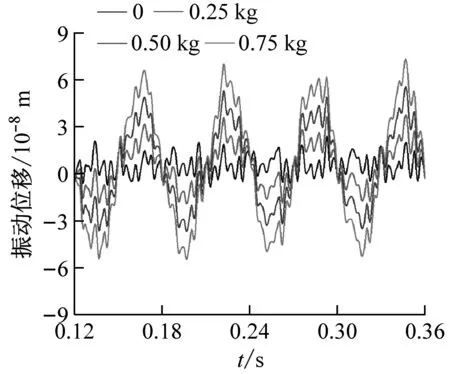
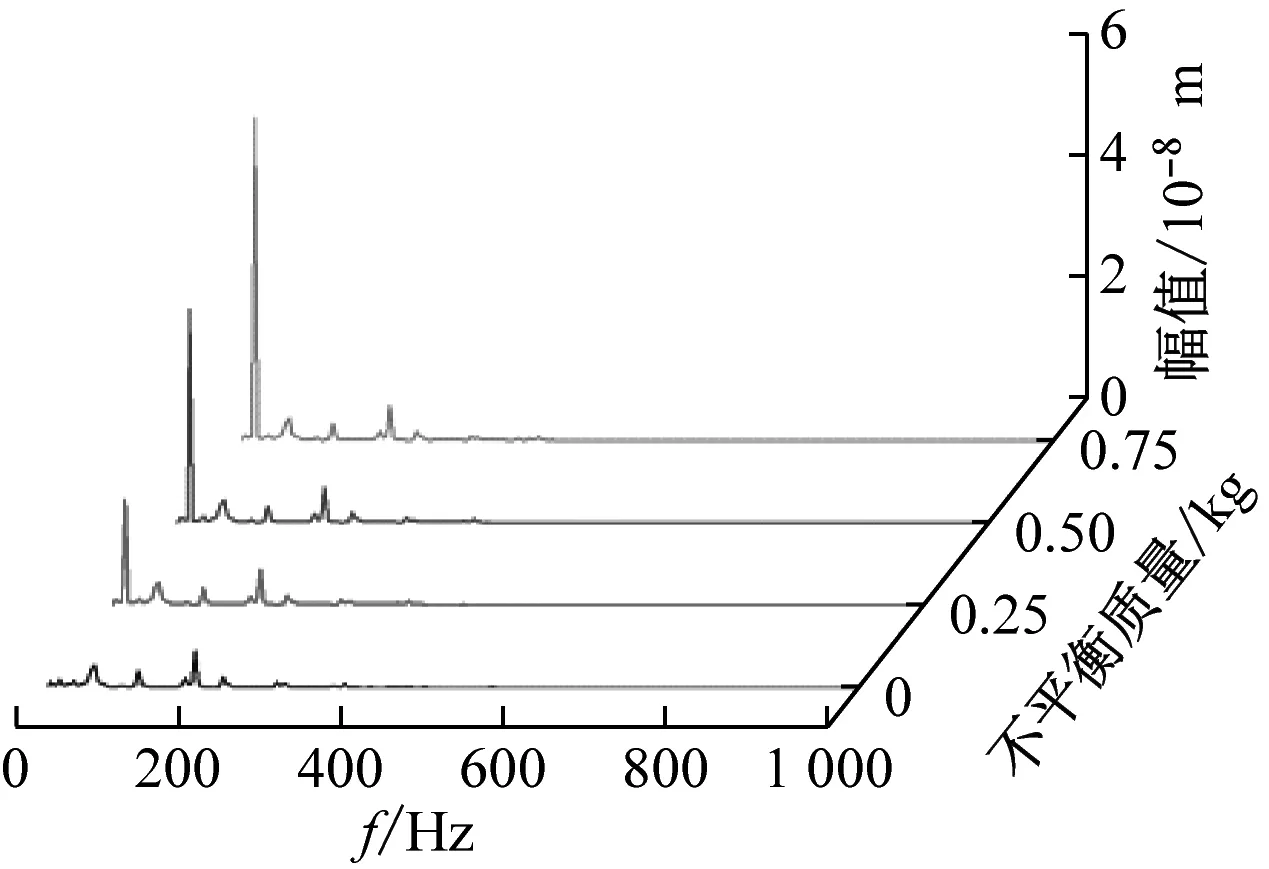
在考虑流体激振力作用下对叶轮不同严重度的不平衡状态特性进行了分析。图8分别给出了4种不平衡质量下叶轮3个轴承处的振动位移响应，从图中的振幅大小可以看出左端轴承P1及中间轴承P2受不平衡质量影响严重，且周期明显，右端轴承P3由于距离叶轮位置较远，影响较小；同时也可以看出，随着不平衡质量越大，各轴承处振动幅值也越大。

(a) P1

图9给出了各轴承处振动位移信号对应的频谱分析结果，从图中可以看出：在不平衡质量条件下左端轴承P1及中间轴承P2处1倍频明显，且随着不平衡质量增大，1倍频幅值也随之增大；而右端轴承P3由于距离叶轮较远，该处振动信号受不平衡质量的影响较弱，其主频为182.6 Hz，是轴频11倍，可知流体激励力是其主要激振源。

4 总结

(1)喷水推进泵叶轮表面流体激振力具有多种频率成分，其中幅值最大的是11倍频，对应导叶叶片数，其次是1倍频，最后是2倍频。

(2)仅考虑流体激励时，靠近叶轮的中间轴承振动最大，其次是右端轴承，左端轴承则振动最小，而振动信号的主频为轴频的11倍，次频为1倍频。

(a) P1

(3)考虑流体激励下叶轮不平衡不同严重度下的振动特性时，发现：靠近叶轮的左端及中间轴承受不平衡质量影响较为严重，且随着不平衡质量增大，其振动幅值和1倍频幅值也随之增大；而远离叶轮的右端轴承受不平衡质量影响较小，且其激振源主要为流体激励。