基于Rényi熵的铣削过程稳定性预测研究
2022-05-11李忠群段林升肖检冬张伟峰
李忠群,刘 浪,段林升,肖检冬,张伟峰
(湖南工业大学 机械工程学院,湖南 株洲 412007)
1 研究背景
作为一种高效的切削加工方式,铣削被广泛应用于航空、航天及汽车制造等领域中。颤振是切削过程中的自激振动现象,它会制约铣削加工质量与加工效率,如在工件表面留下振纹,降低零件表面质量,严重时可能会损坏刀具和工件,甚至机床主轴。研究颤振的首要目的是根据稳定性叶瓣图选取切削参数,进而实现无颤振高效切削。
目前,颤振稳定性分析方法可归纳为频域分析和时域分析两大类。频域分析方法由于在分析过程中进行了近似处理,故处理速度较快,但是处理精度有限。时域分析方法由于综合考虑了非线性切削力、刀齿跳离切削区以及过程阻尼等非线性因素的影响,因而分析精度较高[1]。时域分析方法主要有数值求解法、半离散和全离散求解法等。其中数值求解法应用较广,它通过先求解铣削过程的动力学微分方程,获得切削、刀尖位移等时间历程参数,再施用某种稳定性判据,进而确定当前切削条件的稳定性。数值求解法直观、简单,但稳定性判据的有效性则成为该方法是否可行的关键。
数值求解法常用的稳定判据主要有FFT(fast Fourier transform)法、动态力比静态力法[2]、刀尖位移统计法[3]以及峰值力法等,其中FFT法的运用较为广泛。FFT法适合处理周期信号或平稳信号,而不适合处理切削振动信号[4]。刀尖位移统计法将样本方差作为颤振判定标准,但是在小径向切深情况下预测精度欠佳。相较静态力法,动态力只能对某一工况颤振稳定性进行判断,适应性较差。吴石等[5]以最大Lyapunov指数为判据,分别通过等高线法、轮廓法确定铣削颤振稳定域。Sun Y.W.等[6]则将特征值是否大于1作为稳定性判据。李忠群等[7]提出了一种用于预测铣削稳定性的基于三阶龙格-库塔法的半解析方法,利用Floquet理论判断特定切削状态下的稳定性。但是上述颤振稳定性时域判据,都无法满足在所有工况下都能准确识别颤振的要求,因此需进行改进。
鉴于颤振发生的典型特征是能量在频率轴分布的改变,因此越来越来多的学者运用基于能量的方法在线判断颤振现象。Rényi熵可准确反映切削过程中的能量变化,故本文先采用变步长龙格-库塔法求解铣削动力学微分方程,然后采用Rényi熵分析其时间历程参数,获得铣削过程稳定性叶瓣图,以期为实现无颤振高效切削工艺提供参考。
2 变步长龙格-库塔法求解铣削动力学微分方程
常用欧拉法或龙格-库塔法求解铣削过程动力学微分方程。欧拉法将切线端点作为下一步起点,其计算效率较高但精度较低。而龙格-库塔法因将求解区间细分,并对斜率进行加权平均,作为导数近似,故其在求解精度上有较大改善。本文采用变步长龙格-库塔法求解铣削动力学微分方程,以确保计算精度,降低截断误差,减少计算量。
机床刀具系统的动力学微分方程可表示如下:
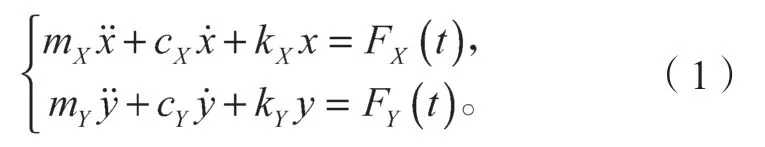
式中:X、Y分别为进给方向及其法方向;
mX、mY分别为X、Y方向系统模态质量;
cX、cY分别为X、Y方向系统阻尼;
kX、kY分别为X、Y方向系统模态刚度;
FX(t)、FY(t)分别为X、Y方向上刀具所受切削力。
以X方向为例,其微分方程可转化为

其初始条件为


以变步长龙格-库塔法求解铣削过程动力学微分方程描述[8]如下:
针对式(2),在[tn,tn+1]时间内,以步长h,运用龙格-库塔法求振幅x的近似值,记为,此时截断误差为O(h5),因此:

将步长h折半,[tn,tn+1]时间内,分两次求得近似值,记为,每次截断误差为c(h/2)5,因此:
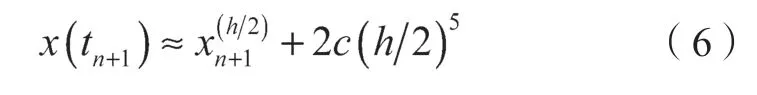
对比式(5)(6),可得两者的误差关系如下:

由式(7)可知,若求解区间步长缩短一半,则截断误差变为原来的1/16。故采用变步长龙格-库塔法求得的振幅近似值为

而将步长折半后两次计算的偏差为

对于给定精度ε,步长选择也不同。当ε>Δ时,将步长反复折半并计算近似值,直至误差小于给定精度,此时的近似值即为最终结果;当ε<Δ时,将步长反复加倍并计算近似值,直至误差大于给定精度,再将此步长值进行折半处理并计算,所得近似值即为最终的结果。
同理,可以得到Y方向的最终计算结果。
通过上述方法,获得给定切削条件下的铣削时域信号,通过施用某种时域稳定性判据,就能判定当前的切削条件是否稳定。按一定的增量改变主轴转速和轴向切深,重复上述过程,就能得到稳定性叶瓣图,其仿真流程如图1所示,其中动态切削厚度与瞬时切削力的详细计算见参考文献[9]。

图1 铣削稳定性数值求解流程图Fig.1 Flow chart of numerical solution of chatter stability for milling process
为了验证上文所述方法求解所得结果的准确性,对不同条件下的槽铣进行切削仿真分析。仿真所用刀具为φ12的硬质合金整体铣刀,刀齿数为2,螺旋角β=30°,铝合金AL7075-T6工件材料,切削力辨识系数如下:切向切削力系数Ktc=796.0 N/mm2,径向切削力系数Krc=168.0 N/mm2,轴向切削力系数Kae=222.0 N/mm2,切向刃口力系数Kte=27.7 N/mm,径向刃口力系数Kre=30.8 N/mm,轴向刃口力系数Kae=1.5 N/mm。该条件下得到的仿真结果如图2、3所示。


图2 转速为8 000 r/min、轴向切深为0.2 mm、每齿进给量为1.5 mm时的仿真结果Fig.2 Simulation results under specific cutting conditions(n=8 000 r/min,ap= 0.2 mm,fZ=1.5 mm)
铣铣削过程中,稳定切削时,切削信号幅值波动收敛;而颤振时,切削信号幅值会大幅增长。由图2所示稳定切削时切削力和刀具振幅仿真结果可以得知,稳定切削下X、Y、Z方向的切削力信号波峰分别为 100, 250, 70 N 左右,波谷约为-150, -10 , -5 N。X、Y方向刀具振幅波峰分别约为 0.008, 0.021 mm,波谷约为-0.002, -0.014 mm ,而且无论是切削力还是刀具振幅,在整个切削过程中,波峰波谷值变化不大。由图 3 所示颤振时切削力和刀具振幅仿真结果,可以得知,0.018 s 前,切削力和刀具振幅信号的波峰和波谷均保持在一个稳定值。之后,刀具振幅和切削力值大幅增长,并经过一段时间后稳定,X、Y、Z方向切削力信号波峰分别约为 2 000, 4 000, 1 000 N,波谷约为 -2 800, -50, -10 N 。X、Y方向刀具振幅波峰分别约为 0.3, 0.5 mm,波谷约为-0.38, -0.40 mm。图 2 和 3 所示仿真结果很好地反映了铣削过程的特点。因此,图2 和 3 可证明本文所提求解铣削过程微分方程的方法是正确。
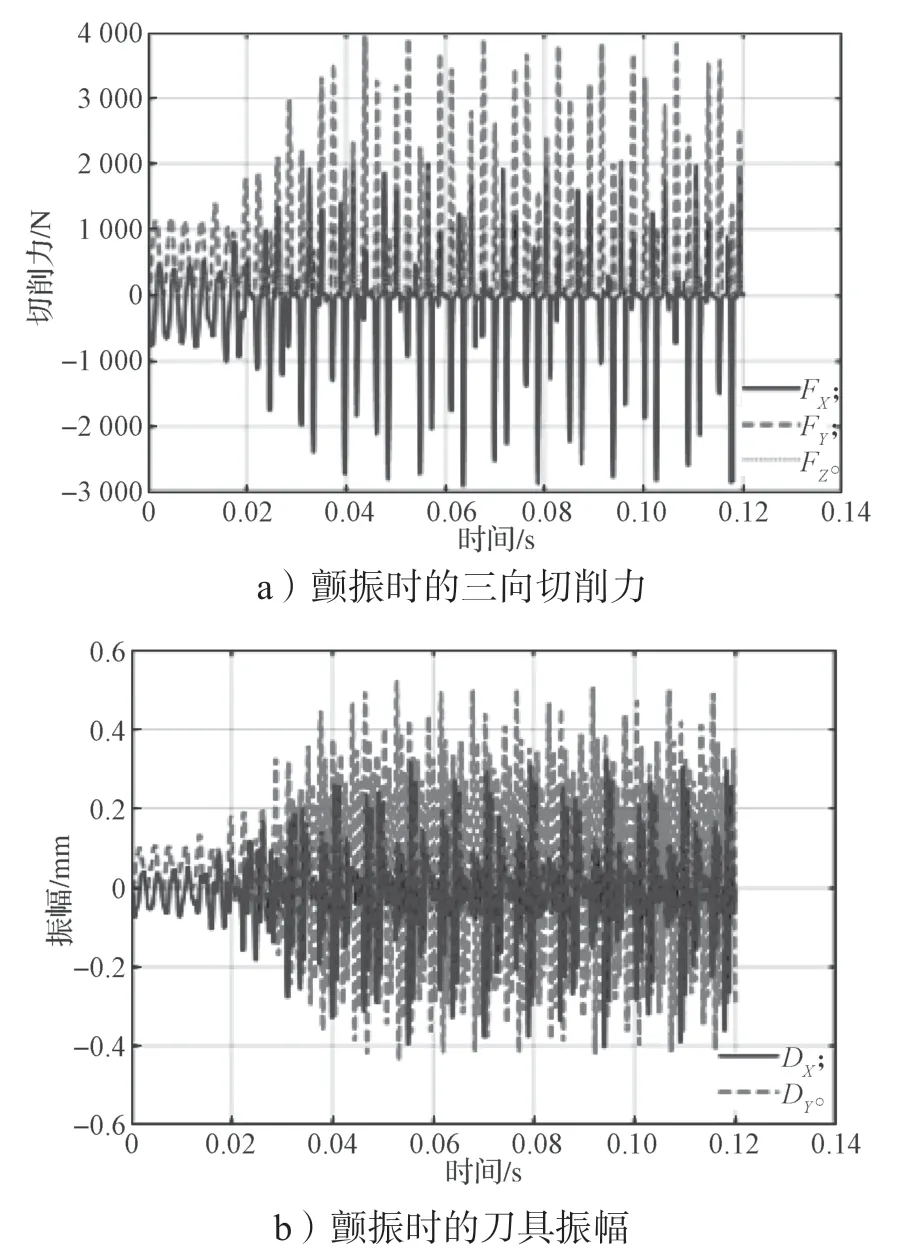
图3 转速为10 000 r/min,轴向切深为0.9 mm,每齿进给量为1.5 mm时的仿真结果Fig.3 Simulation results under specific cutting conditions(n=10 000 r/min,ap= 0.9 mm,fZ=1.5 mm)
3 基于Rényi熵的时域稳定性判据
3.1 Rényi熵定义
熵在数学和信息学中分别用来表示问题的不确定性和系统的复杂性。问题的不确定性和复杂性越大,熵值越大,反之越小。作为熵推广的Renyi熵,可用于判断信号信息量和复杂度,被广泛用于图像配准[10-11]、无线电频谱感知等信号处理领域。Rényi熵是一个无量纲指标,当概率集的所有值几乎相等时,Rényi熵值较大,对应系统复杂度较大;若只有少数值较大,其他值较小,则Rényi熵值较小,对应系统复杂度较低。
时域信号x(t)的Rényi熵计算过程如下:
1)计算时域信号x(t)的幅度谱,为

式中:N为数据长度;
X(ω)为x(t)的频谱。
2)通过归一化处理,可估计出频谱的概率密度函数,为
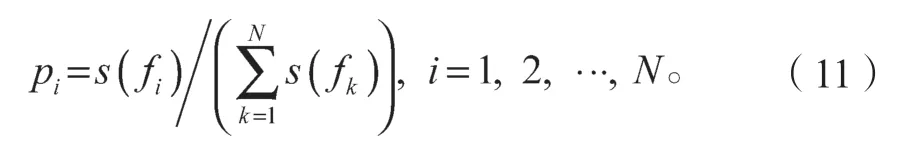
式中:s(fi)为频率分量fi的频谱能量;
pi为相应的概率密度。
3)计算相应的Rényi熵H,定义为
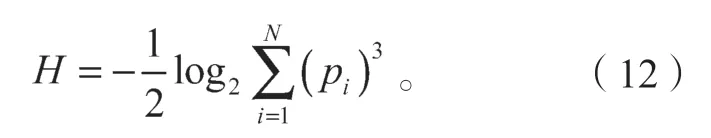
为了比较不同的工作条件,用系数log2N进行归一化处理,可得归一化处理后的Rényi熵E为

3.2 阈值确定
Rényi熵E经归一化处理后是(0,1)范围内的无量纲指标,其中,1表示不确定性最大,0表示不确定性最小。
为揭示Rényi熵是否可检测颤振,并进一步确定颤振阈值,根据颤振稳定性叶瓣图分别选取稳定状态和非稳定状态所对应的切削参数进行铣削过程时域仿真,并计算其Rényi熵。仿真参数设置如下:铣刀直径D=12 mm,刀齿数N=2,螺旋角β= 30°,Ktc=796.0 N/mm2,Krc=168.0 N/mm2,Kte= 27.7 N/mm,Kre= 30.8 N/mm,工艺系统模态参数见表1。稳定与非稳定状态下刀尖振动位移及Rényi熵见图4、5。

表1 工艺系统模态参数Table 1 Modal parameters of the process system

图4 稳定切削条件下的振幅及其Rényi熵Fig.4 Amplitude with its Rényi entropy under a stable cutting condition
图4显示,稳定切削时,信号的Rényi熵除开始时存在少许波动外,都一直稳定在0.9左右,能量主要消耗在切削频率及其谐振频率上,确定性较大。图5显示,在非稳定即颤振切削时,Rényi熵值开始时约为0.9,但随着切削进行,进入颤振状态,能量不仅消耗在切削频率及其谐振频率上,并且有部分能量消耗在颤振频率上,其Rényi熵值逐渐减少,直至在0.8左右上下波动,即铣削颤振发生时,Rényi熵的值为0.8左右。

图5 颤振条件下的振幅及其Rényi熵Fig.5 Amplitude with its Rényi entropy under a cutting condition
为进一步揭示颤振发生时的阈值,改变铣削的轴向切深,计算不同轴向切深下对应的Rényi熵,并且计算不同切削状态下从稳定到颤振的Rényi熵,所得结果如表2所示。
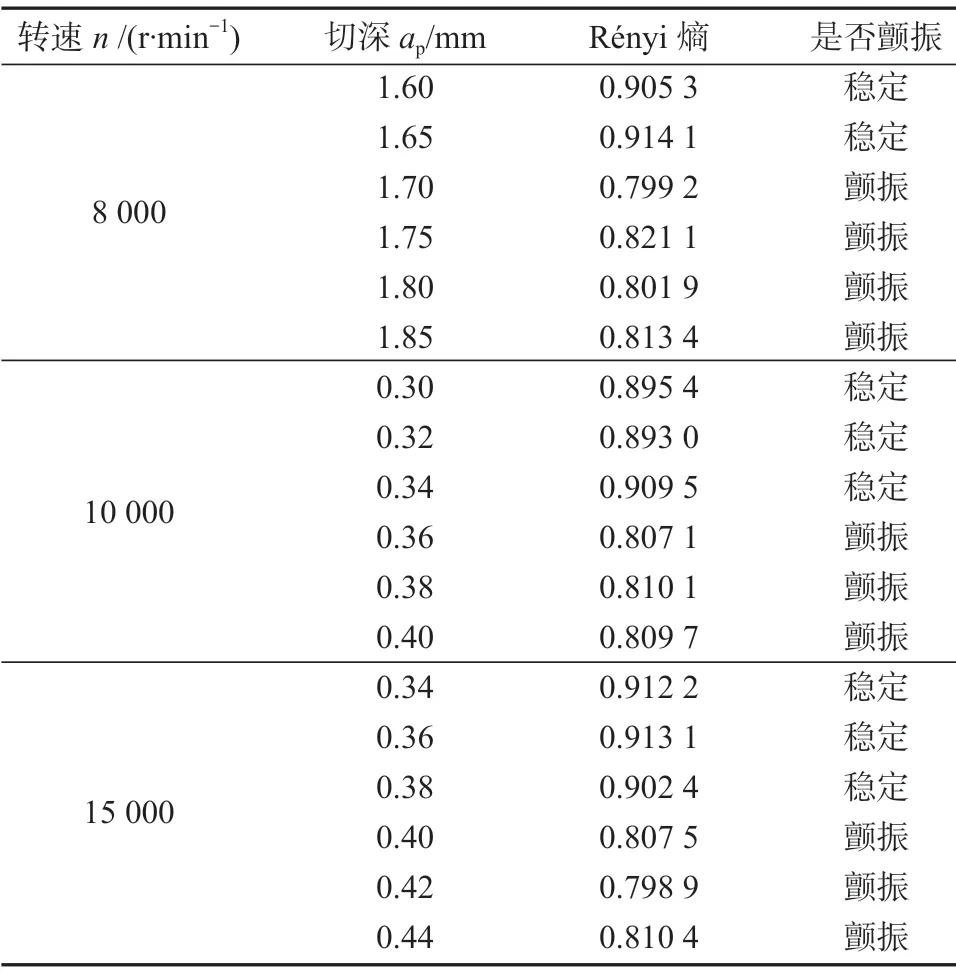
表2 切削状态与Rényi熵的关系表Table 2 Relationship between cutting state and Rényi entropy
表2显示,稳定切削时的Rényi熵在0.9左右;当颤振发生时,Rényi熵在0.8左右。因此,本文将发生颤振的Rényi熵阈值设为0.83,低于该值,则判定为有颤振现象发生。
4 仿真与试验验证
为验证本文提出的Rényi熵稳定性阈值及基于Rényi熵的铣削过程稳定性预测方法,在铣削稳定性时域仿真的基础上进行稳定性验证试验。验证试验在五轴加工中心Mikron HSM/600U上进行,所用刀具为直径12 mm、螺旋角30°、2齿硬质合金整体铣刀,工件材料为AL7075-T6,由切削力系数辨识试验得到切削力系数同前一节,通过锤击试验获得的工艺系统模态参数如表1所示。
在进行颤振验证试验时,首先固定主轴转速,将初始轴向切深设定为ap=0.07 mm,然后以0.03 mm的步长逐渐增加,直至监测到切削颤振,然后改变主轴转速重复上述过程。通过监控切削再生及观察已加工表面是否产生振纹来确定加工过程中是否产生颤振。基于Rényi熵的铣削稳定性叶瓣图预测结果与切削实验结果对比如图6所示。图中,细实线为基于Rényi熵方法仿真得到的稳定区与颤振区分界线,图线下方为稳定切削区,上方为颤振区;方块点为试验稳定切削点,圆圈点为试验颤振切削点。该图显示,铣削过程颤振稳定性仿真结果与实验结果较为一致,从而验证了本文提出的基于Rényi熵的铣削过程颤振稳定性预测方法及用于判定颤振的Rényi熵阈值是正确的。
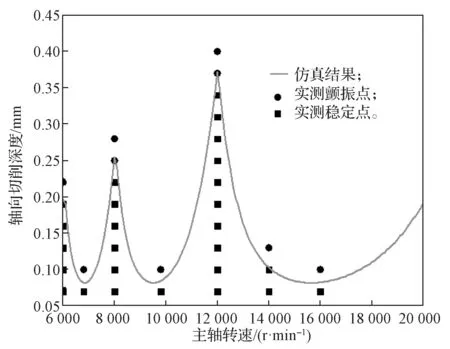
图6 基于Rényi熵的铣削稳定性预测结果与实测结果对比Fig.6 Comparison of milling stability prediction results based on Rényi entropy with measured results
5 结论
1)考虑再生作用的铣削动力学微分方程,运用变步长龙格-库塔法求解,可获得诸如切削力、刀具振动等较为准确的铣削过程时域信号;
2)Rényi熵可以被作为一种判断铣削过程稳定性的有效判据;
3)作为铣削过程稳定性判据的Rényi熵,其阈值为0.83。
