考虑经济功能性的风电场储能系统容量配置
2022-05-11陈晓光杨秀媛卜思齐徐智蔷
陈晓光,杨秀媛*,卜思齐,徐智蔷
(1.北京信息科技大学自动化学院,北京市 海淀区 100192;2.香港理工大学电机工程学系,香港特别行政区 九龙 999077;3.英国南安顿大学物理工程学院,英国 南安普顿 SO17 1BJ)
0 引言
在清洁替代、经济补贴、规划建设及高效运行等数十项政策的有效支持下,截至2020年年底,我国风电总装机居全球第一,累计装机规模达到28 172 万kW,其中新增装机容量高达7 167万kW,且2020年12月占比为65.6%,约为前11个月占比的2 倍。根据国网能源研究院预测,2050 年清洁能源的发电占比将会达到75%[1-2]。同时,大规模风电接入电网后会带来系统的稳定性问题、并网后的电能质量问题、系统发电计划和调度问题,以及系统调峰问题[3-7],将会给电网系统带来巨大的挑战。因此采用一种新型的调节方式,将高比例风电安全稳定地接入电网具有重要意义[8-9]。
储能系统具有双向吞吐功率的能力,即快速存储和及时释放电能,这种调节方式具有灵活、快速的特点,可用于减小新能源的波动、促进新能源消纳、缓解高峰负荷压力等。此外,习近平主席在第75届联合国大会提出,中国的二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和,而清洁能源是完成这一目标的中坚力量,基于该目标,国家电网公司提出:一方面通过电力物联网来扩展新能源消纳的规模;另一方面进一步加快储能系统建设,使系统具备灵活调节能力,提高电能质量的同时提升储能系统运行效益。
现阶段储能系统的应用和配置主要聚焦于储能系统的主要结构介绍、不同种类下储能系统的优势和储能技术在电力系统中的功能作用[10-12]。在实际工程中,由于地理位置、技术和经济等多方面的制约,储能系统无法无限制地满足电力系统的需求[13-14]。当容量配置较小时,无法确保电能质量且系统协调运行性能也会随之下降;而当储能容量配置很大时,初始成本资金和运行维护费用也会提高,因此对于储能系统容量配置方案的研究,在考虑应用功能性的同时,引入经济效益分析更具有合理性。综上所述,将经济性评估引入储能系统容量规划中从而得出合理的配置方案,是当前研究热点。
本文对储能系统经济性评估方法和评价标准进行归纳,对储能容量配置的三大方法进行总结,并对比分析各类方法的优势与不足。最后指出储能配置今后的研究方向,为后续研究提供理论借鉴。
1 储能系统经济性评估
1.1 经济性评估方法和评价标准
经济性评估是直观评判该项目对社会影响大小、资源消耗水平的有效途径[15-16]。经济性评估方法常采用确定性评估,并根据是否引入资产时间价值分为静态评估方法和动态评估方法。同时,从项目投资回收时间、效益价值和资金使用效率方面,可以将经济性评价标准分为时间型、价值型和效率型,其中:时间型标准以时间为计量单位;价值型标准以货币价值作为计量单位;效率型标准以资源产生的效率作为评价指标,如表1所示。目前,储能系统容量配置研究中典型的评价指标有:投资回收期(时间型标准)、现值和年值(价值型标准)和内部收益率(效率型标准)[17-23]。

表1 经济性评价标准Tab.1 Economic evaluation criteria
1.2 投资回收期
投资回收期代表了资金成本回收速率,具体是指项目投入运行后,用每年的净利润补偿其初始期的全部购置成本所花费的时间。
1.2.1 静态投资回收期
采用静态投资回收期指标时,忽略资产的时间价值,即项目投入建设起至项目投入运行后,利用每年获得的净利润抵消项目初期所有资金成本所需要时间。静态投资回收期表达式为

式中:CI为资金收入;CO为资金支出;Ty为静态投资回收期。
1.2.2 动态投资回收期
利用动态投资回收期指标时,引入资产的时间价值,即项目投入建设起至项目投入运行后,在预设的基准收益率下,利用每年获得的净利润现值抵消项目初期所有资金成本现值所需要时间。动态投资回收期表达式为
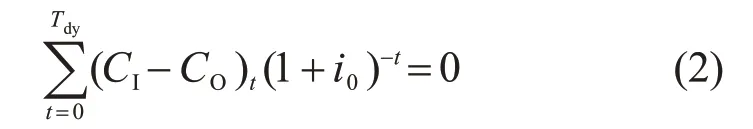
式中:i0为基准收益率;Tdy为动态投资回收期。
1.2.3 投资回收期评价准则
用投资回收期指标进行经济性评估时,需将式(1)、(2)计算出的投资回收期与标准投资回收期进行比较,若计算出的投资回收期小于标准投资回收期,则方案可行;否则,方案不可行。
1.3 现值和年值
1.3.1 费用现值和净现值
现值法分为费用现值和净现值,具体是指在项目建设后每年的资金花费和运维费用或者净现金流量,通过基准折算(收益)率折算成初期的现值,再比较总和的评价方法。费用现值P和净现值PN分别表示为:

式中:COt为第t年的资金支出;T为项目方案给定的寿命时长;CI-CO为净现金流量。
用该指标评价储能系统方案时,费用现值越小,说明花费总资金折现后越少,代表方案经济性越好。当PN>0时,说明该方案在满足预定效益指标的同时还有剩余利润,经济性合理有效;当PN=0 时,表示该方案恰好收支平衡,经济性一般,通常不采用;当PN<0时,代表该方案不满足经济性标准,有亏损。
1.3.2 费用年值和净年值
年值法具体是指在项目建设后每年的资金花费和运维费用或者净现金流量,通过基准收益率折算成等额年值的评价方法。费用年值Y和净年值YN分别表示为:

采用该指标评价储能项目方案时,费用年值越小,说明经济性越好;净年值同净现值类似,当YN>0时经济性合理有效。
1.4 内部收益率
内部收益率代表了项目方案对初始成本资金或者贷款利率的抵消能力,具体是指在方案给定的寿命时长内净现值为零时的折现率。其经济意义为,在该收益率下,项目方案至期末时利用每年的净利润恰好抵消全部初始投入资金。
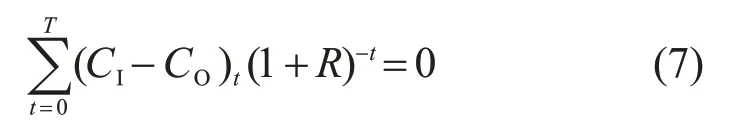
式中R指内部收益率。
利用该指标评价储能系统项目方案时,需要对比内部收益率R与基准收益率i0的大小,当内部收益率更大时,从经济角度表示未回收资金盈利能力更强,经济性合理;反之,说明经济性欠佳,不予采用。
1.5 经济性评价指标对比分析
投资回收期指标反映了资金的回收速度,公式计算简单,但也有一定局限性,如初始期资金成本回收后储能项目的收益情况不能进行定量分析,储能项目使用年限未纳入考虑范围等,因此该标准可以作为次要标准使用。
现值优势在于将资金的时间价值纳入考虑范围,并在项目方案给定的寿命时长内定量分析了其效益情况,通过货币金额的方式直观表现出来;其不足在于基准收益率的选取,不同收益率得出的现值大小不同。年值法与现值法均需要设置基准收益率,但年值法的优越性在于不用考虑方案的寿命时长,在比较寿命时长不同的方案时,现值法需要转换分解周期,年值法可以直接进行比较。
内部收益率与现值法、年值法类似,均引入了资金的时间价值和给定寿命时长内的效益情况,优势在于无需提前设置收益率;其不足在于,与价值型评价标准以货币金额展示方式相比,内部收益率结果展示形式不直观。
2 储能系统配置方法
储能系统配置一是需要结合储能系统功率特性,制定相应的功能性、经济性评价标准;二是根据评价标准选择相应的控制算法和配置方法。目前,储能系统配置方法主要有理论分析法、控制仿真求解法和模型求解法3种。
2.1 理论分析法
理论分析法的前提是基于历史数据分析,再根据选取方法或特征量的不同来确定储能容量[24-29]。
文献[25]采用一阶低通滤波平抑方法,推导出储能系统所需要的容量为滤波时间常数与风电场额定容量的乘积,但是储能初始状态的不同是否会影响功能效果尚有待验证。文献[26]中指出,风电频率在0.01~1 Hz是需要平抑的主要部分,且超级电容容量选取的影响因素为一阶滤波时间常数和频率为0.01 Hz风电最大波动幅值,从而计算出储能系统的配置方案。文献[27]中将原始风功率进行傅里叶变换,通过频谱分析确定需要平抑的风功率频率区间,将储能进行平抑工作时的最大补偿功率作为额定功率,储能容量差最大值与荷电状态(state of charge,SOC)安全区间的比值作为容量范围。文献[28]根据“风电场具备一次调频功能时其调频容量至少为2%额定功率”的要求,由历史数据分析计算出额定功率,再通过功率和容量的关系得出装机容量与储能系统容量的配比。文献[29]中,为满足风电波动标准,通过对风电波动量进行积分,计算出储能系统容量的区间值,根据燃气轮机的台数得出压缩空气储能电站的容量配置。
由以上研究可知,理论分析法分析逻辑清晰,从技术理论层面得到配置方案,有较强的理论支持。但理论分析法推导过程较困难,且风电具有不确定性,会导致理论分析法得出的方案产生偏差,同时实际工程中着重考虑运行效益,缺乏一定合理性。
2.2 控制仿真求解法
控制仿真求解法基于风电场的控制策略对储能系统进行配置,首先获取风电目标出力值,结合风电实际功率得出储能系统的预补偿计划,通过能量状态反馈控制给予修正,确定满足功能应用的最小配置方案[30-36]。
文献[30]采用一种混合储能方式来平抑风电波动,利用小波包分解对原始风电信号进行处理,图1为3层小波包分解示意图,利用高斯分布对高频信号进行数理概率理论分析,求解选取了置信99.7%时混合储能系统的额定功率。文献[35]对不同控制策略下的储能容量配置进行对比,先分析了一阶滤波算法在不同置信区间的储能系统容量配置情况,再与模糊预测控制算法进行对比分析,结果表明,在满足功能性评价指标的前提下,模糊控制所需要容量较小。文献[36]基于我国沿海地区大型风电场连续3 个月的数据,计算得出不同风电场储能系统容量的比例关系,提出了一种大规模储能系统的配置方案。

图1 小波包分解示意图Fig.1 Wavelet packet decomposition diagram
综上可知,控制仿真求解法优势在于基于历史数据完成了运行策略下的功能性需求,使其具有可行性。但该方法对控制策略要求较高,同理论分析法类似,因储能系统运行状态未知,导致实际功能性不可控,此外,由于储能成本较高,缺乏对储能系统的成本和运行效益的详细分析,忽略了实际工程意义。
2.3 模型求解法
模型求解法基于对研究问题的需求不同,建立不同的数学模型,即目标函数和约束条件,经不断优化完善模型,再利用智能算法对模型进行求解计算。目前,针对储能容量配置的模型求解法有单目标模型求解法、多目标模型求解法和双层迭代模型求解法。
2.3.1 单目标模型求解法
单目标模型求解法是目前风电场配置储能容量研究中最常用的方法之一,储能应用的发展本体是价格,如何将经济效益最大化是储能配置的关键。单目标模型求解法通过分析储能系统的成本和效益的组成,建立相应的数学模型,最终求解得到储能配置方案[37],即一个目标函数、k个自变量参数和m个约束条件,数学上定义为

式中目标函数f(x)通常为储能系统的经济成本,其主要由购置初期、运行维护和报废置换3 个阶段产生的费用Cin、Cfun、Cex组成,即
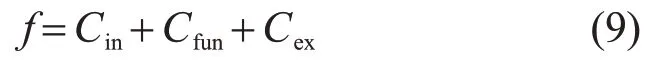
文献[38-41]针对3个阶段的组成部分进行了细化研究,储能系统配置中的自变量参数有2个,分别为储能系统的额定功率值和额定容量值,约束条件常围绕功率、容量和电池荷电状态3 个方面制定,表示如下:

式(10)为功率约束,其中:Pdis,max、Pcha,max分别为电池最大放电、充电功率;Pbat(i)为第i时刻储能系统补偿功率。式(11)为容量约束,其中:Smax、Smin分别为电池最优容量、电池规定的最小容量。式(12)为电池寿命约束,其中:Lcha(i)、Ldis(i)分别为第i时间内连充、连放状态标志;Nmax为电池充放电次数最大值。
文献[38]提出了将运行成本、惩罚成本和固有成本3 部分费用现值最小作为目标函数,利用遗传算法对模型进行求解,分别考虑了有无运行成本的储能系统功能性效果,证明了加入运行成本的必要性。文献[39]中提出“双应用”概念,即削峰填谷和平抑风电波动,在满足双应用的前提下建立全寿命周期的经济模型,在固有成本、运行成本、惩罚成本三者费用年值的基础上加入了报废处理成本。文献[40]中建立了以储能系统月均最低生命周期成本最小为目标函数的经济模型,利用传统的量子粒子群、未加自适应扩张系数的量子粒子群和改进的量子粒子群3 种不同算法对模型进行求解,对比分析3 种算法下的储能配置优劣。文献[41]提出一种光热-抽水蓄能-电池复合储能系统容量优化模型,将储能投资运行成本、系统缺电损失费用和弃风惩罚费用最小作为目标函数,利用粒子群算法进行求解,得出最优的储能配置方案。
以上研究均只考虑了购置、运行和报废3 个阶段的成本组成,忽略了储能系统投入使用后的直接、间接收益。文献[42]采用混合储能系统参与风电一次调频,建立了风储系统收益最大化的数学模型,目标函数中有风储系统售电收益、储能投资年等效值、弃风成本、一次调频服务价值和一次调频不足惩罚成本,并利用鲸鱼算法对模型进行求解。
综上所述,单目标模型求解法建立的经济模型通过经济型评价标准对风储系统进行了较为完善的效益成本分析计算;但由于成本组成元素之间存在制约关系,如购置阶段成本与运行维护成本,购置阶段成本增加,即储能容量增加,相同充、放电量对应的荷电状态值减小,过充、过放现象随之减少,电池寿命相应会提升,运行维护成本降低,风电期望输出的百分比也会上升,惩罚成本也会降低。因此,单个目标函数具有一定局限性,无法对特定组成元素进行寻优。
2.3.2 双层迭代模型求解法
双层迭代模型求解法建立了双层迭代模型,即顶层配置模型和底层运行模型,如图2 所示。与单目标模型求解法不同在于,双层模型中目标函数个数不是单一的,其顶层、底层模型中均有各自的目标函数,且目标函数在时间尺度或者物理意义上有所不同,顶层模型侧重于长时间尺度规划,底层模型侧重于短时间尺度规划,上下模型结果相互迭代,求解储能系统配置方案。数学定义如下:

图2 双层优化模型Fig.2 Bilevel optimization model

式中:y为顶层模型的目标函数;h为底层模型的目标函数;A1,A2,…,An为顶层目标函数的组成部分;k个自变量参数x1,x2,…,xk主要为储能额定功率和额定容量;m个约束条件e1,e2,…,em主要有交流潮流约束、节点电压约束、主网倒送功率约束、储能系统荷电状态约束。
交流潮流约束如下:

式中:Pi、Qi分别为节点i注入的有功、无功功率;Ui、Uj分别为节点i、j的电压;δi、δj分别为节点i、j的相角;Gij、Bij分别为节点导纳矩阵的实部和虚部;N为节点数。
节点电压约束如下:

式中Ui,max、Ui,min分别为节点i电压的上、下限值。
主网倒送功率约束如下:

式中Pgridt为t时刻与主网联络支路上的功率。
储能系统荷电状态约束如下:

式中:ηc、ηd分别为充、放电效率;Pc(t)、Pd(t)分别为t时刻充、放电功率;E为储能系统额定功率;SOCmax、SOCmin分别为储能荷电状态上、下限值。
文献[43]中顶层模型为储能系统的配置决策层,以年综合成本费用年值最小为目标函数,底层模型以日惩罚成本最小为目标函数,利用粒子群算法对双层模型进行迭代求解,通过算例仿真验证配置方案的有效性和经济性。文献[44]重新定义不同置信区间的风险惩罚价值计算,定量评估了灵活性不足造成的经济损失,在此基础上建立了双层优化模型。以上2 个文献处理典型场景的方式不同,文献[43]采用Xmeans 聚类仿真得出典型场景,而文献[44]利用风险价值不同对场景进行分类。上述方法在年综合成本最小的同时,将综合成本中的惩罚成本作为目标函数之一,使成本中的组成元素同步优化。文献[45]指出运行成本和储能额定容量的“黑箱”特性,建立了双层优化模型,结合“黑箱”特性,利用网格自适应直接搜索算法和改进的粒子群算法对双层模型进行分段求解,使得储能系统在满足经济性最优的情况下,运行寿命也能显著提高。
双层迭代模型求解法通常将长时间尺度的问题设置在顶层模型中,将短时间尺度的运行问题设置在底层模型中,与单目标模型求解不同的是,将长时间尺度规划的组成元素细化成底层的目标函数,通过不同优化算法进行寻优,在顶层目标函数达到最优的前提下,结合实际不同问题,细化的元素同时求得最优解。此外,该方法多数情况下将储能布局包含在规划问题中,因此常用于有源配电网的储能配置方案中。但该方法不足之处在于,目标函数必须具有相同单位量纲且个数有限。
2.3.3 多目标模型求解法
文献[46]提出储能成本与平抑效果是一种相互制衡的关系,其先将与目标并网功率偏移量方差最小作为优化目标,以此为前提利用模糊控制理论调整充放电指令,然后建立了惩罚成本和运行成本费用现值最小的优化模型,并采用智能算法进行求解。文献[47]利用配置储能系统来减少弃风,建立了以储能投资成本最小为目标函数,以弃风率为约束的数学模型,采用凸近似和抽样平均构建线性规划方法来求解。以上2 个文献把偏移量方差、弃风率作为前提条件建立单目标优化模型,将多目标转变为单目标模型进行求解,忽略了储能额定容量对偏移量方差、弃风率的影响,无法同时兼顾两者的最优性,求解结果的正确性有待验证。
多目标模型求解法是单目标模型求解法的一种延伸,即b个目标函数、k个自变量参数和m个约束条件,数学上定义如下:

式(21)中,目标函数个数依据实际情况制定,自变量同样为储能系统额定功率和容量,约束条件与单目标模型求解法类似。
多目标涉及到多个目标的优化,这些目标并不是独立存在的,它们往往是通过决策变量耦合在一起且处于相互竞争的状态,而且每个目标具有不同的单位和量纲,因此很难客观地评价多目标问题的解。它们的竞争和复杂性使得对其进行优化变得十分困难。单目标模型求解法通常根据储能系统的经济性建立模型,并进行求解计算,价格虽然是储能系统的关键因素,但储能系统作为一种功能综合体,其功能性作用才是配置储能的根本所在。多目标模型求解法将功能性指标和经济性指标同时作为目标函数进行求解计算,得出的配置方案更具有实际意义。
文献[48]建立了一种经济性较优且运行策略最佳的储能双层多目标规划模型,利用自适应变异的粒子群算法进行双层迭代并对模型进行求解计算,得出最佳储能配置方案。该方法结合了双层迭代模型和多目标模型的特点,将不同单位量纲的目标函数放置于双层模型中。文献[49]将投资成本和运维成本之和最小、平抑波动率同时作为目标函数,采用带有精英策略的非支配遗传算法对模型进行求解计算。文献[50]建立了有功网损、电压偏差、总投资均最小的多目标模型,引入了立方混沌映射、混合蛙跳个体交流机制以及综合满意度评价机制来改进鲸鱼算法,从而求解得出配置方案。
多目标模型求解法改善了单目标模型法和双层迭代模型的局限性,如优化目标单一、优化量单位量纲不同等,但随着优化目标函数的增加,其求解难度也随之增加。
2.3.4 3种模型求解法对比分析
本文对比分析了3 种模型求解法的优势与不足,结果如表2 所示。由于这3 种方法不是独立的,因此在进行配置方法的选取时可以考虑其特点进行适当的结合。
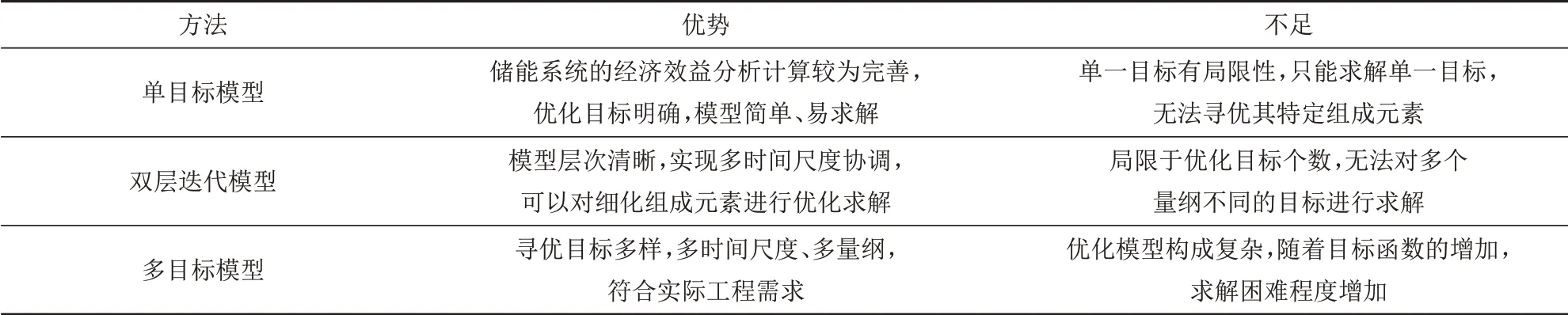
表2 3种模型求解法对比Tab.2 Comparision of three model solving methods
模型求解法针对不同问题建立数学模型并进行求解,引入的经济性评估加速了储能技术商业化。虽然现有研究完善了经济性的组成部分,并通过仿真验证了方法的有效性,但该方法依赖于智能算法,在求解不同优化问题时,如何选取最合适的优化算法使优化效果达到最佳,仍有待进一步深入研究。
2.4 储能系统配置方法对比分析
通过对理论分析法、控制仿真求解法和模型求解法3 种储能系统配置方法进行对比分析,总结出3种配置方法的优点与不足,如表3所示。此外,根据配置方法归纳出储能系统配置的基本流程,如图3所示。

图3 配置储能系统的基本流程Fig.3 Basic flow of energy storage system configuration

表3 3种配置方法对比Tab.3 Comparison of three configuration methods
3 结论
结合经济功能性储能容量配置问题,归纳了储能系统经济性评估方法和评价标准,对比分析了容量配置的三大方法,指出了各方法的优势与不足,给出了储能系统容量配置的基本流程。风电场储能系统为波动性较强、随机性较大的风电并网提供了有效方法,虽然在储能系统配置方法上已有若干成果,但仍有以下方面有待进一步研究:
1)在储能系统容量配置方法中引入储能寿命预测研究。储能系统寿命是评价储能系统运行能力的重要指标之一,在现有的配置方法研究中,一些研究弱化了寿命预测,将经验值作为生命周期值直接代入求解,从而得出配置方案;还有一些研究通过储能系统的最大循环次数来预估系统寿命。而这些研究都是基于测试者预设好的条件下,在实际工作环境、场景下可能会有偏差,尤其是对储能容量变化带来的影响考虑欠佳,如选定储能类别为磷酸铁锂电池,在多次充放电之后,其储能容量逐步减小,导致充放电深度减小,经济性评估可能就会出现偏差。如何将基于不同工况下电池循环运行过程容量及电压衰减特性构建的预测模型引入储能系统配置方案中,还有待进一步研究。
2)计及能源互联网储能综合效益评价体系的建立。储能技术的成本较高,能源市场机制尚不健全,而市场相关方又不能定量分析出储能项目的效益水平,若从风电场出发规划储能系统,仅侧重平滑风电场输出收益,则太过片面且丧失经济性,将减缓储能系统商业化的速度。因此,建立全面的储能综合效益评价体系,可以在国家政策的扶持下促进储能系统的推广。
