多点数值天气预报风速和辐照度集中式修正方法研究
2022-05-11张永蕊阎洁林爱美韩爽刘永前
张永蕊,阎洁*,林爱美,韩爽,刘永前
(1.华北电力大学新能源学院,北京市 昌平区 102206;2.新能源电力系统国家重点实验室(华北电力大学),北京市 昌平区 102206)
0 引言
数值天气预报(numerical weather prediction,NWP)是风电/光伏功率预测模型的关键输入[1-8]。但由于受初始场误差以及中尺度气象模式有限的计算分辨率(地形等局地因素无法在中尺度模式准确描述)等因素影响,NWP 数据可能会与各气象要素实测数值产生较大偏差[9]。此外,辐照度与光伏发电功率间的近线性关系,以及风速与风电功率间的3 次方关系,使得微小的气象预报误差也会造成很大的功率误差[10-12]。因此需要对NWP进行修正,这对于提高风光功率预测精度、保障电网安全稳定运行具有重要意义[13-14]。
目前,国内外关于NWP风速和辐照度修正的研究大都是对风电和光伏进行单独修正,修正方法主要分为2类:一是通过对NWP历史误差的统计进行整体性修正[15-16];二是建立原始NWP 数据和实测数据间的映射关系,从而对未来时刻NWP数据进行修正,如基于高斯过程回归算法[17-19]、核算法[20]、人工神经网络算法[21-23]等建立原始NWP数据和实测数据间的映射关系,但是这些方法大都只考虑到了单一点位NWP 风速/辐照度时序特性,通过建立该点位NWP数据和实测数据之间的映射关系对NWP 进行修正[24-28],而忽略了风光气象数据间的空间相关性。单一点位的NWP数据空间位置单一,对复杂天气条件的适应性有限,无法有效降低NWP数据和实测数据之间映射关系的不确定性。此外,即使考虑到空间相关性,更多地也只是考虑了风速之间的相关性[29-31],而忽略了辐照度以及风光气象数据之间的时空相关性。
事实上,区域内的天气系统具有惯性,风光资源之间存在复杂的时空相关性,能够很好地提供额外信息,以帮助提升NWP 精度,而且NWP可同时提供风电和光伏功率预测所需的风速、辐照度等气象数据。在未来高比例可再生能源并网场景下,大量集中开发的风电场、光伏电站会被并入电力系统,若区域风光资源的时空相关关系不能在模型中充分学习,在一定程度上会限制NWP修正效果。
针对以上研究的不足,本文提出了NWP风速和辐照度的多点集中式修正方法,基于注意力神经网络建立了具有多对多映射结构的NWP风速和辐照度集中式修正模型。引入注意力机制和深度全连接神经网络算法,一方面模型可以得到具有一定时空相关性的多点NWP数据,在训练中能获得更多有效信息,从而降低映射过程中的不确定性;另一方面注意力机制也能够在众多的输入信息中聚焦于对当前任务更为关键的信息,降低模型的复杂度,提高任务处理的效率和准确性。以某区域8 个风电场和7 个光伏电站的NWP 数据和历史风速/辐照度数据为例对所提方法进行验证,结果表明,该方法可同时得出多个点位的NWP修正结果,同时也可有效提高各点位NWP风速和辐照度精度。
1 区域风速和辐照度时空相关性分析
同一区域风光场站多呈现集中式分布特点,受相似地理位置和气候条件的影响,风速、辐照度、温度等气象因素密切相关,存在着一定的时空耦合关系,若能在NWP修正时将此种关系考虑在内,则可实现修正精度的有效提升。因此本文采用Pearson线性相关系数ρ与Spearman秩相关系数ρs对各风电场实际风速、各光伏电站实际辐照度进行定量分析。
假设(Xi,Yi)(i=1,2,…,n)为取自总体(X,Y)的样本,则样本的Pearson线性相关系数表示为

用Ri表示Xi在(X1,X2,…,Xn)中的秩,用Qi表 示Yi在(Y1,Y2,…,Yn) 中 的 秩, 则 样 本 的Spearman秩相关系数表示为
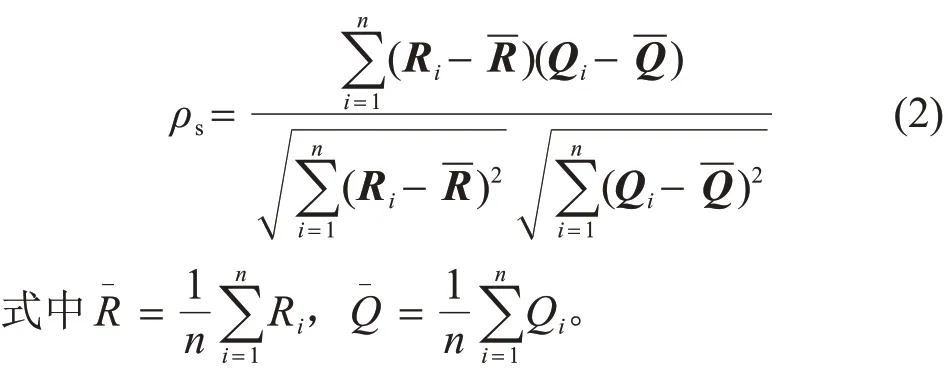
以分布在某区域8 个风电场和7 个光伏电站2019年1月1日至2019年12月31日实测风速和辐照度数据为例进行相关性分析,结果如图1所示,其中:WF1—WF8 分别代表8 个风电场;SP1—SP7分别代表7个光伏电站。从图1可以看出:各风电场间存在一定的相关性,以Pearson线性相关系数为评价指标时,其值从0.46(WF6 与WF8)变化至0.97(WF1 与WF6);各光伏电站辐照度之间呈高度正相关关系,以Pearson线性相关系数为评价指标时,其值从0.74(SP1 与SP7)变化至0.90(SP2 与SP5);8 个风电场风速的Pearson 线性相关系数平均值为0.69,Spearman 秩相关系数平均值为0.68,7 个光伏电站辐照度的Pearson 线性相关系数平均值为0.86,Spearman 秩相关系数平均值为0.90,相关性较强。但是风电场与光伏电站的相关系数在-0.25~0.20,这可能是由于风速和辐照度的整体变化趋势不同。

图1 各风电场风速、光伏电站辐照度相关性Fig.1 Correlation between wind speed of wind farms and irradiance of photovoltaic power stations
2 多点NWP 风速和辐照度集中式修正模型
2.1 NWP
NWP是根据大气实际情况,在一定的初值和边值条件下求解描述天气演变过程的流体力学和热力学的方程组,预测未来一定时段的大气运动状态和天气现象。然而天气系统是不稳定的动力系统,预测值与真实值有一定的偏差;此外,由于许多风电场/光伏电站与气象站存在一定的距离,所获取的数据与当地实际值存在一定偏差。基于此,本文提出一种面向区域的多点NWP风速和辐照度的集中式修正方法。
2.2 NWP风速和辐照度集中式修正模型
2.2.1 注意力机制
在神经网络学习中,通常模型的参数越多,模型的表达能力越强,模型所存储的信息量也越大,但这会带来信息过载的问题。通过引入注意力机制,可降低修正模型的复杂度,在众多的输入信息中聚焦于对当前任务更为关键的信息,降低对其他信息的关注度,提高任务处理的效率和准确性。注意力机制模型计算步骤如图2所示。
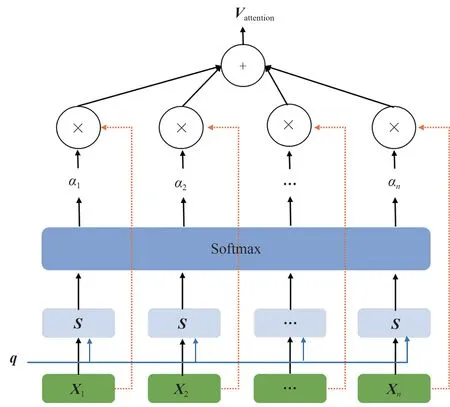
图2 注意力权值计算步骤Fig.2 Steps to calculate the value of attention
基于注意力机制的风光关键输入信息提取过程如下:
1)输入信息X=[X1X2…Xn],这是风电场和光伏电站的NWP数据。
2)注意力分布αi表示在给定查询q时,输入信息向量X中第i个信息与查询q的相关程度,其表达式为
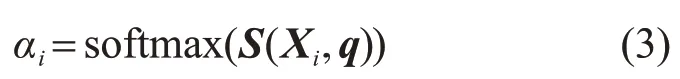
式中:softmax是神经网络的激活函数;S(Xi,q)是注意力打分函数,本文采用点积模型进行打分,表示为

3)信息加权平均,采用软注意力机制对输入信息X进行编码,软注意力机制是指在选择信息时,不是从N个信息中只选择1个,而是计算N个输入信息的加权平均,再输入到神经网络中进行计算,如式(5)所示。
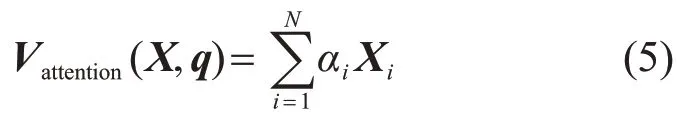
2.2.2 基于注意力神经网络的NWP集中式修正模型构建
基于注意力神经网络的NWP风速和辐照度集中式修正模型中,使用深度全连接神经网络搭建共享隐藏层。深度全连接神经网络所采取的结构和深度学习的相关优化算法可以克服网络出现过拟合或者陷入局部最优解的问题,从而可以深度挖掘数据的隐含特征,拥有更强大的非线性拟合和自学习能力。
与传统神经网络相比,深度全连接神经网络更强调网络的深度,层与层之间采用全连接方式,利用权重系数矩阵W、偏移向量b和输入值向量X进行一系列线性运算和激活运算,从输入层开始,一层层向后计算,计算到输出层,得到输出结果。网络结构中第l层的输出结果Yl可表示为
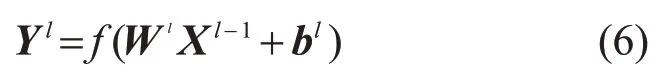
式中:W l、bl分别为全连接神经网络第l层的权重矩阵、偏置矩阵;Xl-1为全连接神经网络第l-1层的输入矩阵;f(·)为激活函数,常见的激活函数包括对数S型函数Sigmoid、双曲正切函数tanh和线性整流函数ReLu。
基于注意力神经网络的NWP集中式修正模型的网络结构和训练机制如图3 所示,具体修正步骤如下:

图3 多点NWP集中式修正模型Fig.3 Multi-point integrated correction method of NWP
1)构建NWP 修正所需输入变量集和输出变量集。输入变量集由风电场群和光伏场群的NWP数据组成,包括风速和辐照度;输出变量集由风电场群的实测风速和光伏场群的实测辐照度组成。
2)基于注意力机制对NWP 修正模型的输入信息进行处理,在更好地提取有效信息的同时降低模型的复杂度。
3)构建基于注意力神经网络的NWP 风速和辐照度集中式修正模型。
4)利用训练集数据对模型进行训练。
5)利用训练好的NWP 集中式修正模型对NWP风速和辐照度进行修正。
在模型参数设置过程中,选用梯度下降法对模型进行优化,模型优化器选用随机梯度下降法(stochastic gradient descent,SGD),激活函数选用ReLu 函数。同时,采用Dropout 方法来避免模型在训练过程中出现过拟合现象;采用批次规范化方法(batch normalization,BN)来减小因各层分布不均和“梯度弥散”而造成的影响,即在每个隐藏层的输出后添加一层规范化层,将输出按照同一批次的特征数值规范化至同一分布。经多次测试验证,基于注意力神经网络的NWP集中式修正模型的最优网络结构参数如表1所示。

表1 隐藏层结构参数Tab.1 Network structure parameters of hidden layer
3 算例分析
3.1 数据说明及评价指标
以中国某区域8 个风电场和7 个光伏电站2019年1月1日至2019年12月31日实测风速、辐照度,以及NWP风速、辐照度为例进行分析,数据的时间分辨率是15 min。根据经验与训练样本比例的灵敏度分析,每月前20 天数据为训练样本,剩余数据为测试样本,这种划分方式能够使测试集跨越整年,从而更合理地评估模型性能。
以均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)为NWP修正精度的评价指标,表示如下:

式中:Vm(t)为t时刻的实际风速/辐照度;VNWP(t)为t时刻的NWP 风速/辐照度;n为数据样本总个数。
为了检验本文所提集中式修正模型的效果,将其与反向传播神经网络(back propagation neural network,BPNN)模型、支持向量机(support vector machine, SVM) 模型和时序卷积神经网络(temporal convolutional network,TCN)模型3 种传统修正模型进行对比分析。同时,为了验证本文提出的多对多集中式映射策略,建立了基于注意力神经网络的单点NWP修正模型。
3.2 结果分析
3.2.1 光伏电站辐照度修正结果
表2、3 分别为不同修正方法下NWP 辐照度均方根误差、平均绝对误差。可以看出,原始NWP 辐照度与实测辐照度有较大的误差(最大值为231.55 W/m2,最小值为115.39 W/m2)。经本文模型修正后,NWP辐照度均方根误差平均值降低了57.99 W/m2,最大值降低了124.88 W/m2(SP3)。与传统的NWP修正方法相比,本文方法在大多数光伏电站中的修正精度较高。此外,与传统的一对一映射模型相比,所提集中式修正模型在大多数光伏电站具有较高的校正精度,NWP辐照度误差平均值降低了24.9 W/m2。
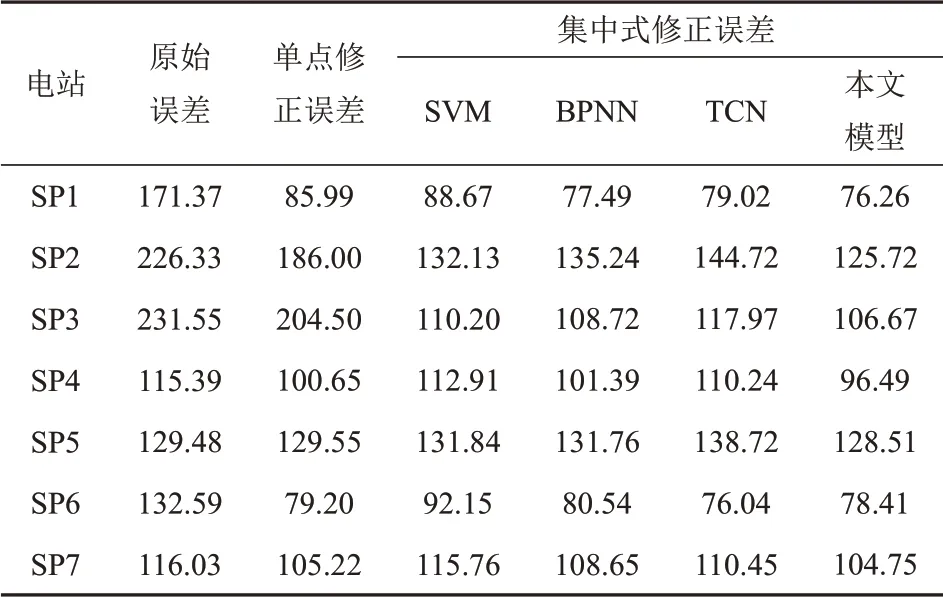
表2 不同修正方法下NWP辐照度均方根误差Tab.2 RMSE of NWP irradiance in different correction methods W/m2
为分析所提集中式修正方法的稳定性,分别计算了其在各月的修正误差,并与原始的NWP辐照度误差进行对比,结果如图4所示。可以看出,所提集中式修正方法的月稳定性较强,SP1和SP2月误差均小于原始误差,其余光伏电站的月误差大部分也小于原始误差。
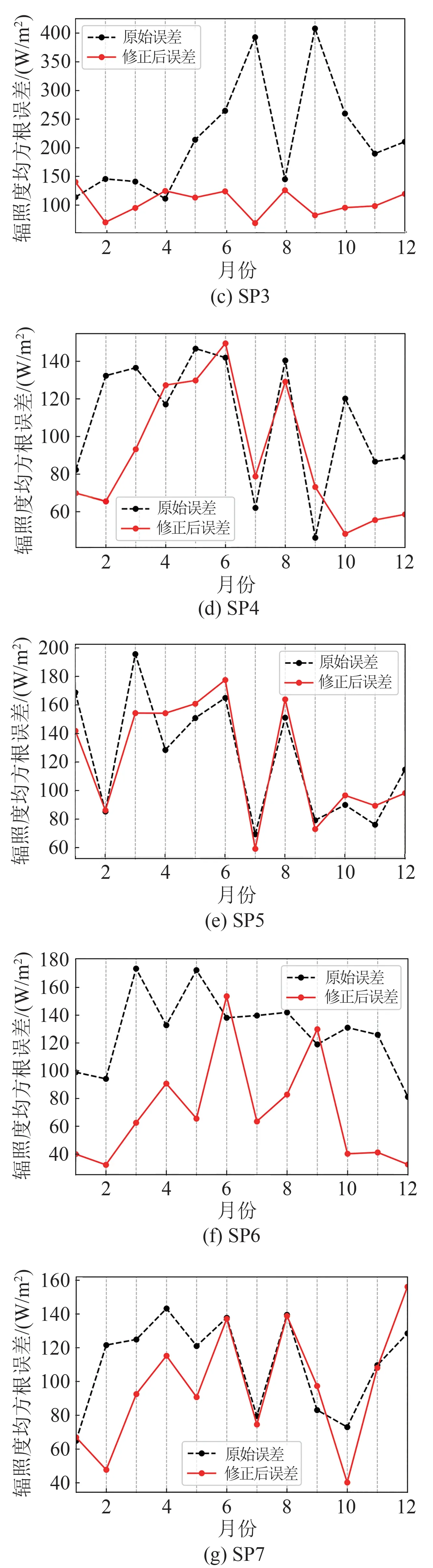
图4 各月NWP辐照度修正误差对比Fig.4 Comparison of NWP irradiance correction error in different months
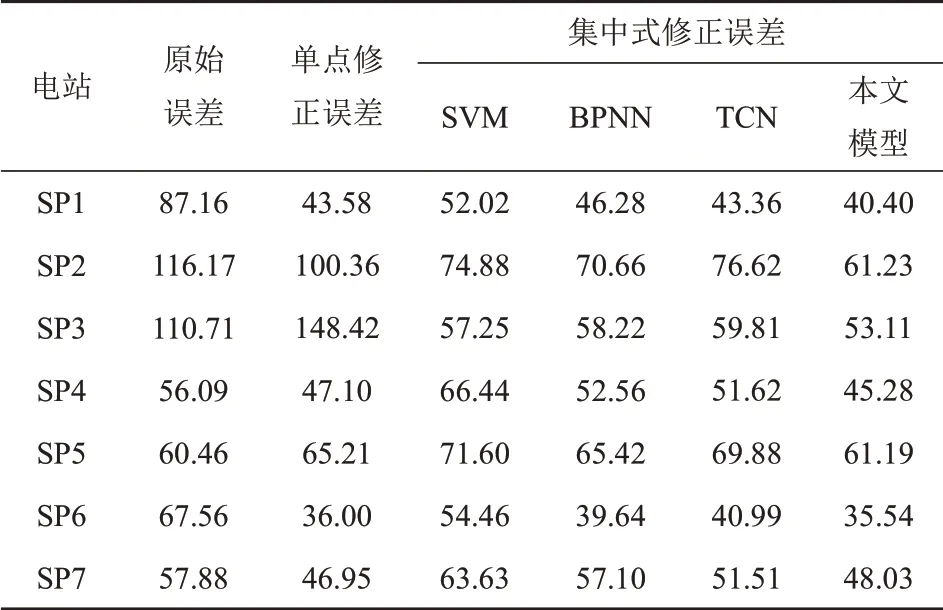
表3 不同修正方法下NWP辐照度平均绝对误差Tab.3 MAE of NWP irradiance in different correction methods W/m2

3.2.2 风电场风速修正结果
表4、5 分别为不同修正方法下NWP 风速均方根误差、平均绝对误差。可以看出,原始NWP风速与实测风速有较大的误差(最大值为3.31 m/s,最小值为2.41 m/s),经本文模型修正后,各风电场风速误差均有一定程度的降低,8 个风电场NWP风速均方根误差平均值降低了0.34 m/s,最大值降低了0.73 m/s。与传统的NWP 修正方法相比,本文方法在大多数风电场中有较高的修正精度。此外,与传统的一对一映射模型相比,本文模型修正效果较好,NWP风速误差平均降低了5.88%。
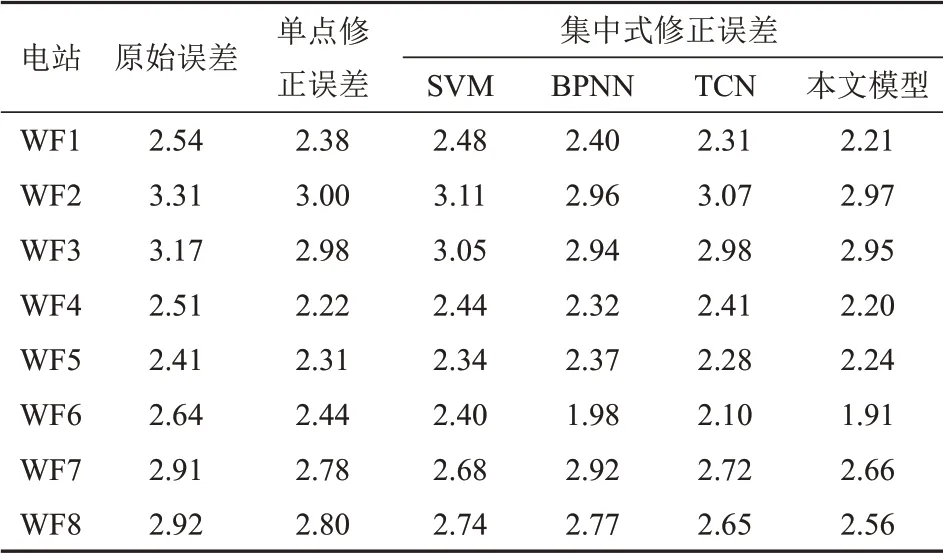
表4 不同修正方法下NWP风速均方根误差Tab.4 RMSE of wind speed in different correction methods m/s
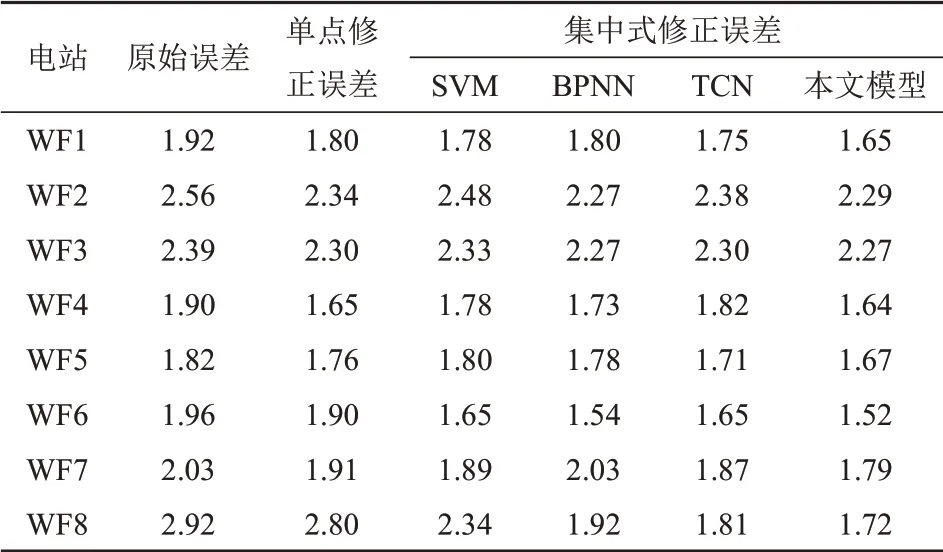
表5 不同修正方法下NWP风速平均绝对误差Tab.5 MAE of wind speed in different correction methods m/s
为分析所提集中式修正方法的稳定性,分别计算了其在各月的修正误差,并与原始的NWP风速误差进行对比,结果如图5 所示。可以看出,所提集中式修正方法的月稳定性较强,8 个风电场的月误差大部分都小于原始误差。此外,相比于光伏场群,风电场群的NWP 风速精度提升较小,这可能是由于光伏电站之间时空相关性较强,在修正的过程中能捕捉到更多的有效信息,从而降低了模型映射过程中的不确定性,提高了NWP的精度。
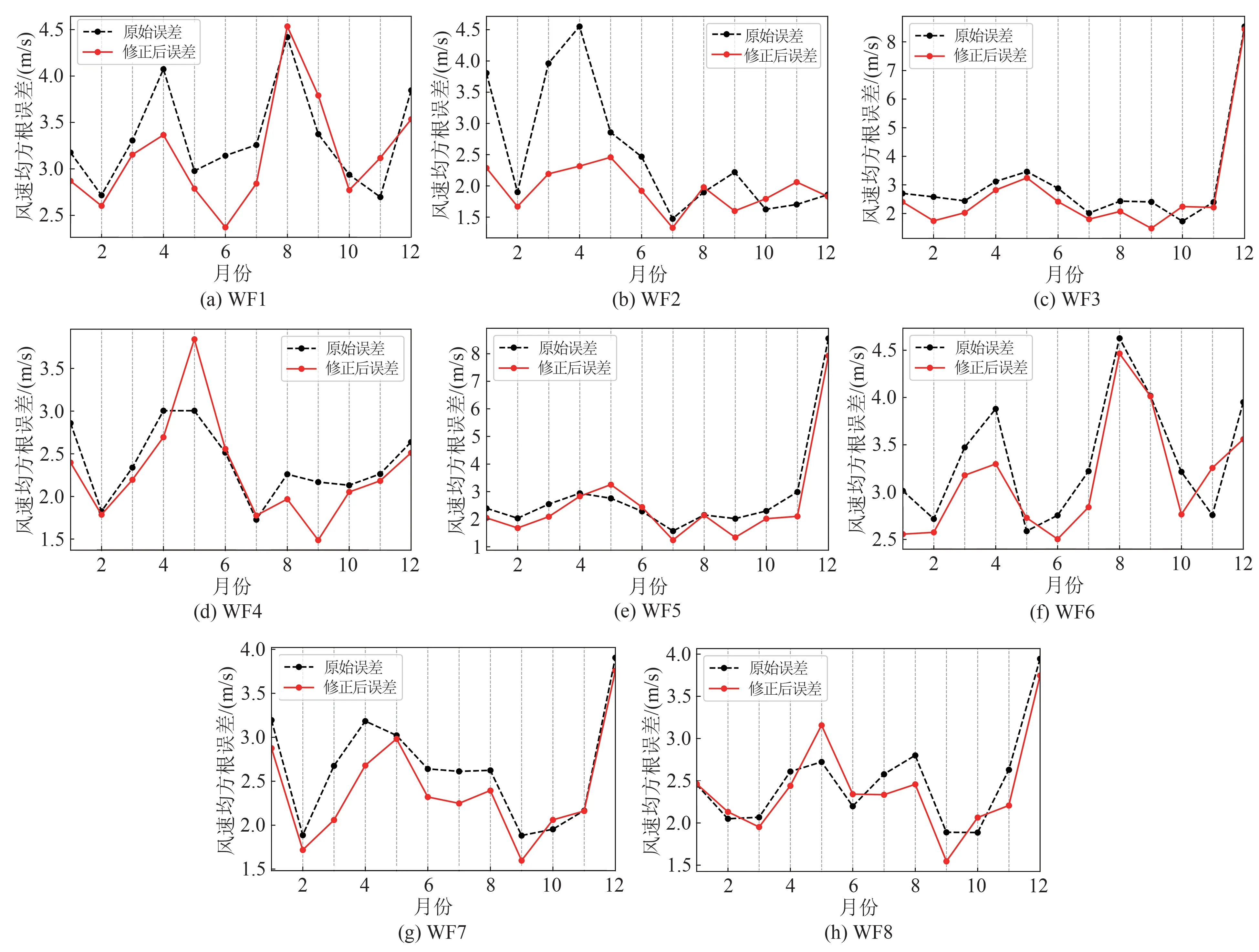
图5 各月NWP风速修正误差对比Fig.5 Comparison of NWP wind speed correction error in different months
4 结论
为了提高区域内NWP 风速和辐照度的准确性,提出了一种基于注意力神经网络的多点NWP风速和辐照度集中式修正模型,通过与传统的单点NWP修正模型进行对比分析,得到以下结论:
1)基于注意力神经网络的NWP 集中式修正模型可同时得出多点NWP风速和辐照度的修正结果,且修正效果优于传统修正模型,验证了该模型的有效性。
2)与传统修正模型相比,NWP风速误差平均降低了5.88%,NWP辐照度误差平均降低19.48%,从而验证了集中式修正模型对于风光资源时空耦合特性的学习效果。
3)区域内光伏电站间辐照度相关性强于同区域内风电场间风速相关性,所对应的光伏电站辐照度的修正效果更好,表明考虑资源时空相关性的多对多映射模型能够有效提升修正效果。
然而区域内其他气象因素(如温度的差异性)会对风速和辐照度修正产生一定的影响,在后续的研究中,将会进一步融合温度等因素,优化所提模型和算法,以提高模型的普适性。
