一种改进的旋转矢量姿态更新算法*

耿腾飞 刘 明

（云南民族大学 昆明 650031）

1 引言

自1971年Bortz提出旋转矢量微分方程后[1]，有大量学者对圆锥误差补偿算法进行了一系列的研究[2～7]，有效地提高了姿态解算的精度，然而上述算法表达式都是基于陀螺的角增量信息，近年来新型陀螺仪输出大多为角速率形式，将原有算法直接应用到角速率陀螺算法误差会变大。针对上述现象，文献[8～9]对硬件增强角速率输入圆锥算法做了深入研究，详细推导了基于角速率输入的圆锥算法误差补偿系数的通式。文献[10]对周期项的误差补偿进行再次优化，提出一种改进的姿态算法。文献[11]提出了一种同时把角速率和角增量信号作为输入的圆锥误差算法，提高了算法精度，此外还有许多文献研究角速率输入的圆锥误差算法[12～13]。文中详细推导了角速率输入的圆锥误差补偿系数的表示方式，在此基础上利用陀螺前周期角增量信息得到了改进的求解圆锥误差补偿系数的算法，具有一定工程应用价值。

2 圆锥误差算法优化准则

3 角速率圆锥误差补偿算法

4 改进圆锥补偿算法

5 应用

下面给出1～4子样圆锥误差系数，结果见表1。

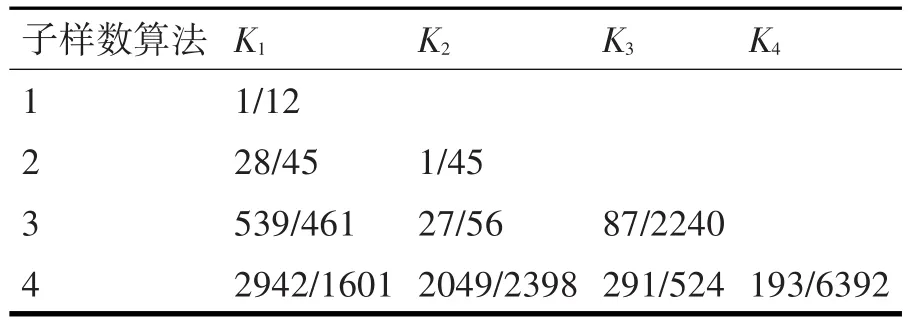
表1 1～4子样圆锥误差系数

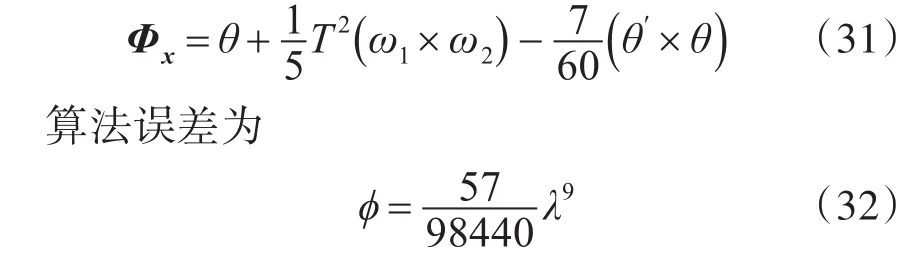
通过比较式（28）和式（32）可以看出同子样数的改进算法精度高于常规算法，更加实用。

以N=2时的算法为例，分别对传统算法和改进算法进行模拟仿真，取a=1°，h=0.02s，算法误差与圆锥频率之间的关系如图1所示。

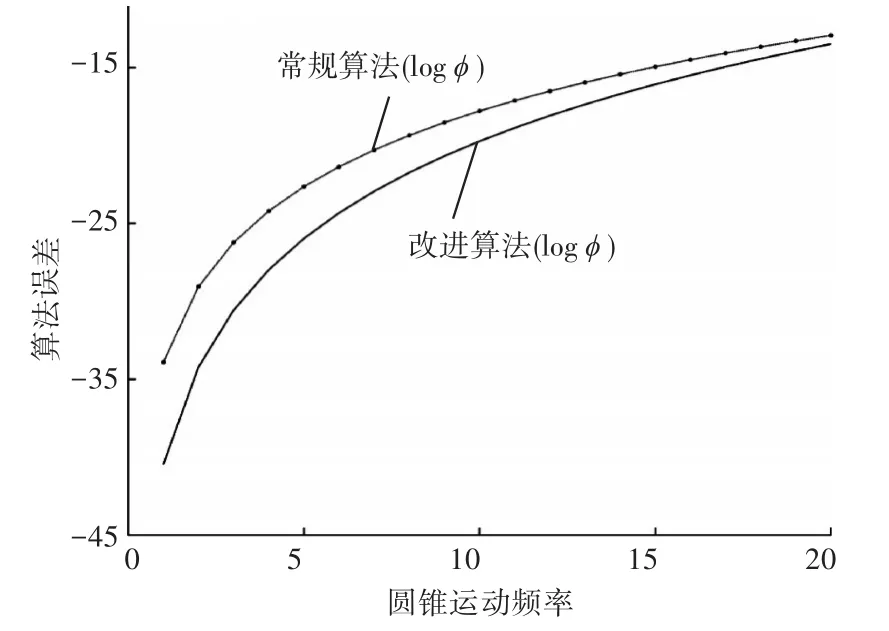
图1 算法误差与圆锥运动频率的关系

由上图可以看出，两类算法误差都随着圆锥运动的频率增大而增大，但是在频率相同的情况下，改进算法的算法误差与传统算法相比有明显的降低。

6 结语

文中详细推导了纯角速率输入下的圆锥算法公式，并给出了误差补偿的一般公式，列出了1～4子样的补偿系数，并在此基础上提出了一种改进的角速率圆锥误差补偿算法，可求得任意子样数下的补偿系数方程和误差表达式，通过比较可知新算法有明显的优势，具有一定的应用价值。