基于相关性的传感数据分析与处理

罗 宇， 李 颖， 郝昕宇， 杨光松

（1 贵州省广播电视局645 台， 贵阳 550200； 2 集美大学 诚毅学院， 福建 厦门 361021；3 集美大学 信息工程学院， 福建 厦门， 361021）

0 引 言

随着信息技术的快速发展，处理数据的能力不断增强，目前商用的云存储平台已经具有存储大量数据的能力，如何对海量数据进行分析，己成为当前的一个研究热点。 为了对环境传感数据进行监测，获取不同时间、不同空间的数据信息，将分布在不同地域的传感器节点，依靠通信协议组网，最终通过特定网关，将获取的数据传输到云平台上，通过分析数据之间所存在的相关性，寻找其固有的规律。

利用数据相关性的检测，可以为监测工作提供精准且全面的数据支持。 通过研究数据相关性来制定策略，从而采取相应的处理措施，在环境工程、环境生物学和地球科学等方面得到广泛应用。 在水利方面，利用往年的数据可以分析雨季何时来临；在地理方面，可分析出降雨量对土壤成分的影响，预防泥石流的形成；在农业中，可以分析出哪一种变量会影响农作物的产量或者甜度，从而可以用安全的方式增加产量或者提升口感；在环境监测方面，降雨数据、臭氧密度、气温温度等数据之间都存在相关性，其中任何一个量的变化都会引起其他一种或者几种分量的变化。 因此，需要对所有变量进行相关性分析，从而发现变量之间的关联关系。

本文主要从协方差、时间序列分析、互相关等方面，讨论相关性的计算、估计方法，并以环境监测数据为例进行相关性分析。

1 相关性及协方差

相关性是指事物之间存在相似的程度。 相关关系是指变量之间存在的一种不确定的数量依存关系，即一个变量的数值发生变化时，另一个变量的数值也相应地发生变化，变化的数值不是确定的，但在一定的范围内。

协方差是一种用来度量两个随机变量关系的统计量，假设有两类数据x和x， 可将其视为随机变量，两者之间的关系可以由一个联合概率密度函数（x，x） 来表示，与（x，x） 相关的协方差矩阵C可定义为式（1）：

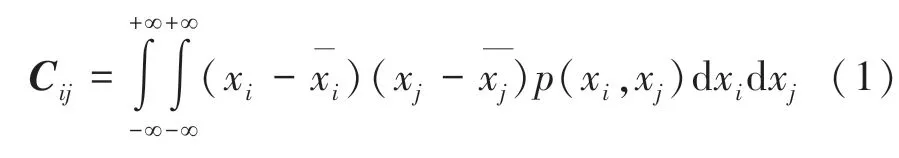
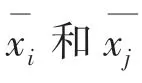
通常，可以通过观测数据构造的近似概率密度函数方块图来估计C。 协方差估算的散点图，如图1 所示，可将（x，x） 平面划分为许多小的方格，按照编号。 每个方格的面积为ΔxΔx， 其中心坐标为（x（），x（））。 于是可得式（2）：

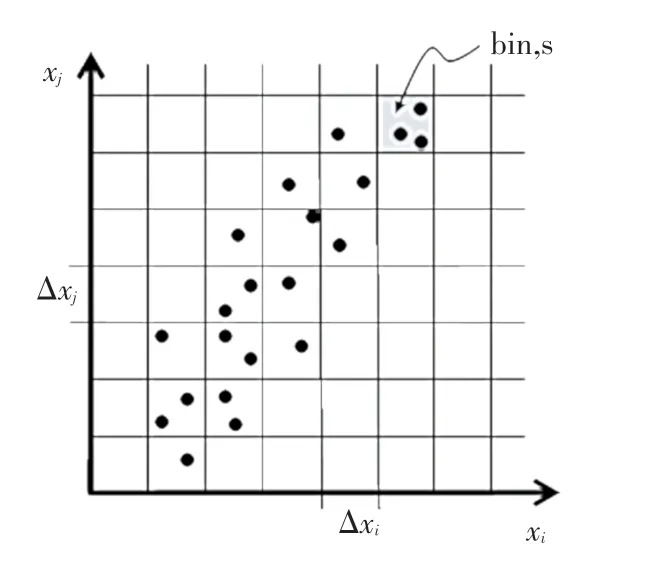
图1 协方差估算的散点图Fig.1 Scatter plot of covariance estimation

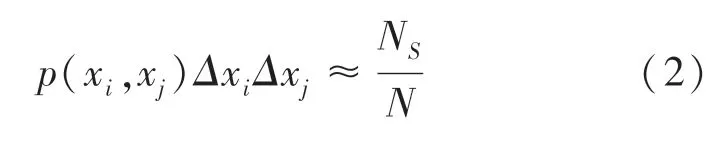
其中，表示平面中数据对的总数，N表示方格中数据对的数量（即互相关的数目对）。

综合考虑（1）式和（2）式，可得C的近似计算公式（3）：

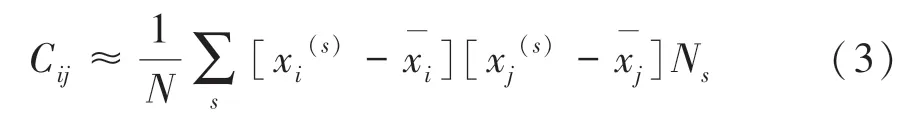
进一步进行规一化处理，将方格大小缩小，使其每个方格中至多有一个数据对（0 or1），于是可得式（4）：

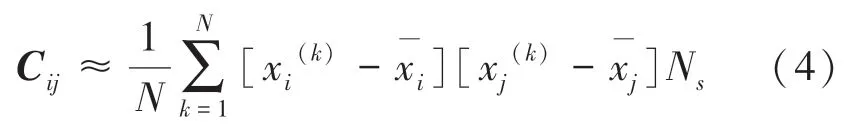
当数据表现出一定程度的相关性时，协方差是非0 的，但其实际数值取决于数据量。 通过方差乘积的平方根进行缩放，可将范围标准化为1，式（5）。

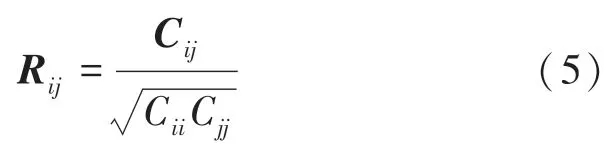
被称为相关系数矩阵，其元素称为相关系数。 当通过某个数据集对其进行估计时，被称为样本相关系数。

2 时间序列的数据相关性

式（1）的协方差矩阵C可以用于量化联合概率密度函数的相关度，亦可用于描述时间序列的相关度。 将式（1）展开，可得式（6）。

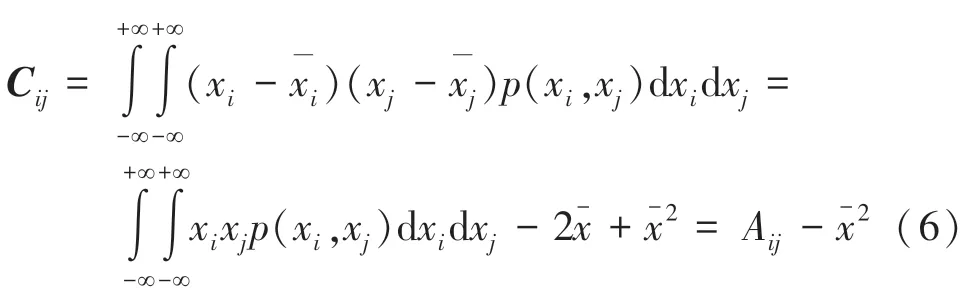
其中，A被称为自相关矩阵，式（7）。

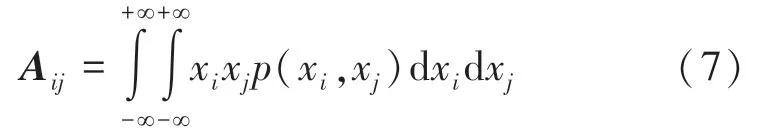
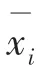
用类似式（2）～式（4）的方法，可以用散点图的形式求式（7）的近似积分，于是可求得A的近似值为：

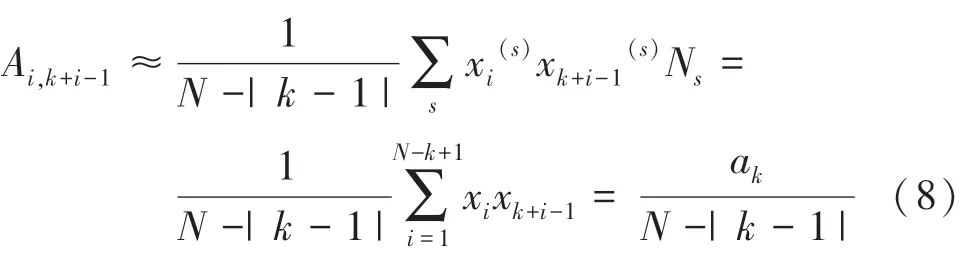
其中，a为在时间差1 时的自相关，式（9）。

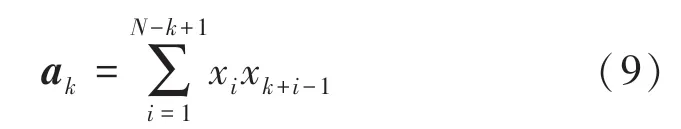
由a构成的列向量称为时间序列的自相关。由于是对称的，所以时间间隔为正的自相关等于时间间隔为负的自相关，即当∣∣1 时，A ＝a。

3 互相关

自相关研究的问题是从相同变量的时间序列中间隔时延的样本；而互相关研究是不同变量的时间序列中间隔时延的样本。 例如降水和河水流量的时间序列，在降水量高的时候，可以预计河水流量也会很大。 但由于河水流动需要时间，因此，当降水时间序列相对于水流时间序列时间间隔一定时间时，降水时间序列与水流时间序列的相关性最大。已知变量和， 定义互相关性为其概率密度函数（u，v），分别为时间序列的第个样本，和时间序列的第个样本。

可以将自相关的计算，类推到计算互相关c，式（10）

互相关可用如式（11）的卷积形式进行计算。

与自相关不同的是，互相关在时间间隔上是不对称的。（） 和（） 的互相关性是（） 和（） 的互相关的时间反转。

4 数据处理与分析

在现实生活中，不同事物之间存在大量的因果关系，通过发掘这些相互关系，可以获得一些有用的信息，帮助做出正确的判断，有助于科学的预测，从而防患于未然。

分析北京市2017 年一整年的空气质量数据，见表1。 主要基于协方差、自相关、互相关进行分析。

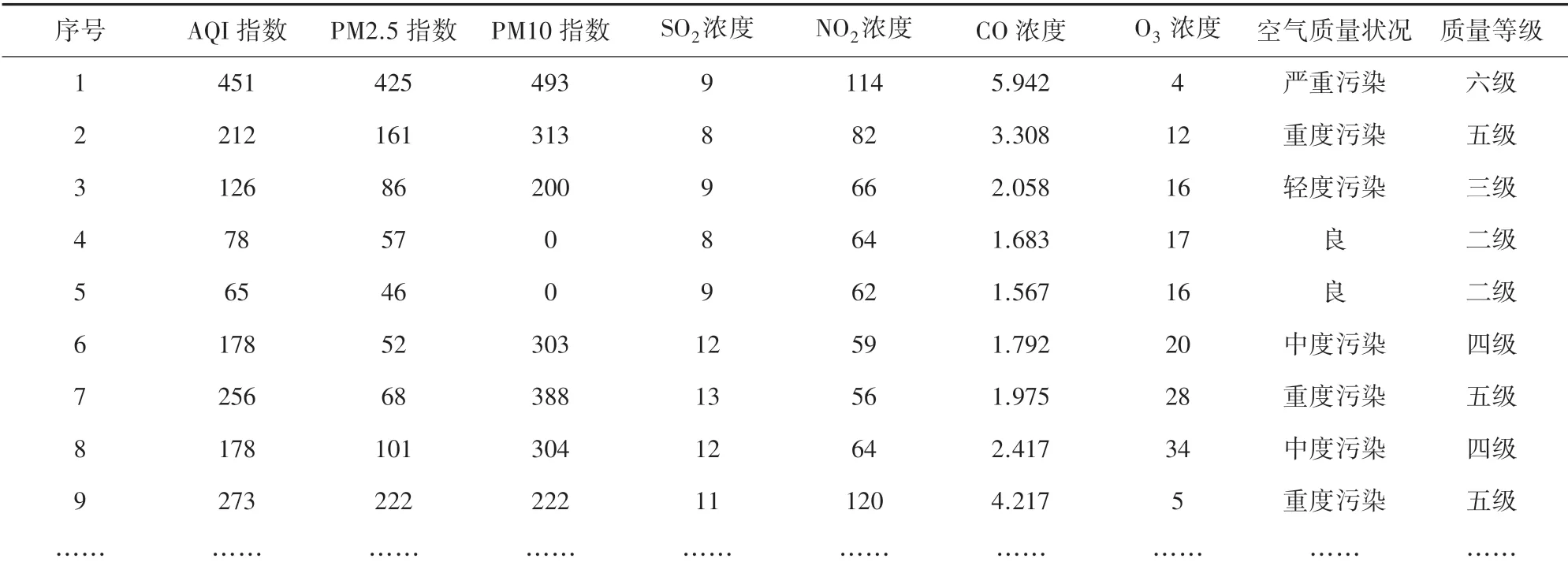
表1 北京2017 年环境监测数据Tab.1 Environmental monitoring data of a year in Beijing

4.1 基于协方差的数据分析

空气质量数据包含大气中一些污染物的含量，如：PM2.5（细颗粒物）、PM10（可吸入颗粒物）、SO（二氧化硫）、NO（二氧化氮）、CO（一氧化碳）、CO（二氧化碳）、O（臭氧）。 空气质量的衡量标准是空气质量指数（Air Quality Index，AQI），选取其中5 种污染物做相关协方差分析，相关系数矩阵如图2 所示，横轴和纵轴分别表示这几种因素之间的相关系数，颜色越深，表示相关性越强。 可见，从左上至右下的对角线元素都均为黑色，因为每种因素与自身完全相关，与AQI 最相关的因素是PM2.5，其次是PM10、CO、NO，SO与其相关性较小。

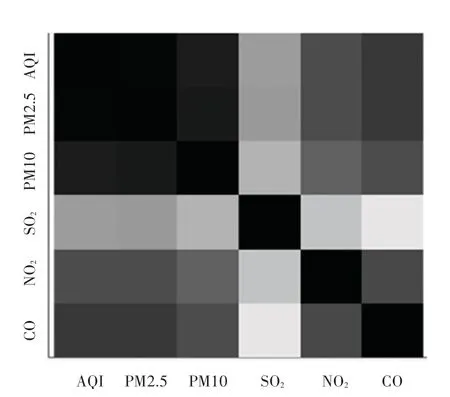
图2 北京市空气质量数据集相关系数绝对值矩阵Fig.2 Absolute value matrix of correlation coefficient of Beijing air quality dataset

根据表1，进一步绘出AQI 与PM2.5 的相关指数，如图3 所示，两个因素呈现正相关的趋势，利用式（5），可计算出PM2.5 与AQ1 相关系数0.99，证明PM2.5 与AQI 具有高度相关性。

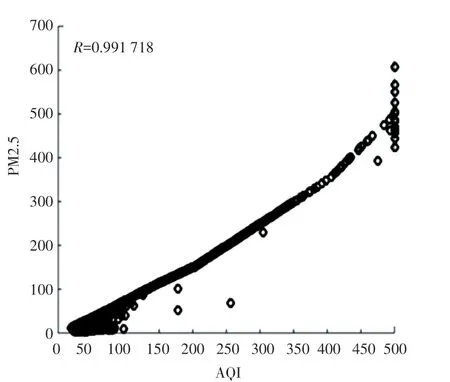
图3 PM2.5 和AQI 的相关性Fig.3 Correlation between PM2.5 and AQI

由此说明，若想改变空气质量指数，治理PM2.5最有成效，因为其相关性最大，降低PM2.5 指数可以有效的改变空气质量；改变PM10 在空气中的含量，也可以提升空气质量。

4.2 基于自相关的数据分析

PM2.5 在时间序列上自身的变化，时间间隔越大则自相关越小。 根据表1，取不同时刻的PM2.5 的指数值，可得空气中PM2.5 的指数与时间间隔的关系，如图4 所示。 图4（a）～（c）分别是时间间隔为1 d、3 d、30 d 的自相关函数，横轴为PM2.5 的含量，纵轴为滞后一段时间后的PM2.5 含量。

如果把空气在t时刻PM2.5 含量记为d，在t时刻的含量记为d， 那么其联合概率密度函数为（d，d），可以预计那个d和d在何处有很强的正相关关系，当时间间隔Δtt很小时，其相关性很强，短期时间关联度很高，比如昨天的PM2.5 与今天的PM2.5 差不多，如图4（a）所示；当测量值的时间间隔大时，其PM2.5 的相关性变得越来越小，如图4（b）为间隔3 天的情况；在一定时间间隔（如1 个月左右的时间）后，基本不相关，如图4（c）。

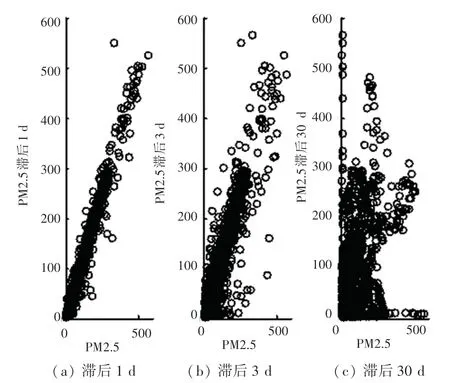
图4 空气中PM2.5 的含量与时间间隔的关系Fig.4 Relationship between PM2.5 and time interval

4.3 基于互相关的数据分析

互相关是表示两个变量之间相似性的一个度量，通过与已知变量比较，来寻找未知变量中的特性。 利用互相关性分析臭氧和日照的关系。

平流层中的臭氧，能够吸收紫外线，保护地球表面免受太阳紫外线的照射。 但对流层中的臭氧是雾霾的主要成分，对人体健康有害，并导致的AQI 指数降低。

利用半个月的数据，仅包含4 列数据，时间（d）、臭氧（ppb）、太阳辐射（W／m）和气温（c）。

将半月的日照数据（单位为W／m）和臭氧变化，在同一地点按对应的时间进行统计，如图5 所示。 可见两者都表现出明显的周期性，随着日照的强度增大，臭氧浓度也会增多，这是因为在温度较高、日照相对较强时，大气中的氮氧化物和挥发性有机化合物经紫外线照射发生光化学反应，生成臭氧。随着时间序列的变化，这两个变量所反映出来的相关性成正相关性，只要日照强度高，臭氧浓度就会增多。 另一方面，从图5 亦可以观察到，臭氧峰值比日照峰值延迟了几d（见垂直虚线）。

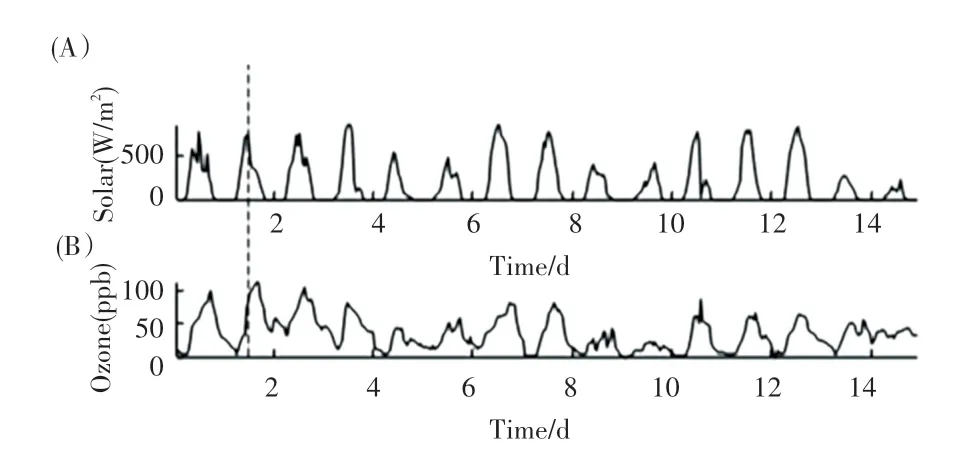
图5 日照与臭氧含量的相关图Fig.5 Correlation between sunshine and ozone content

进一步将两个时间序列相互关联，可得出滞后的时间间隔约为3 d，如图6 所示。

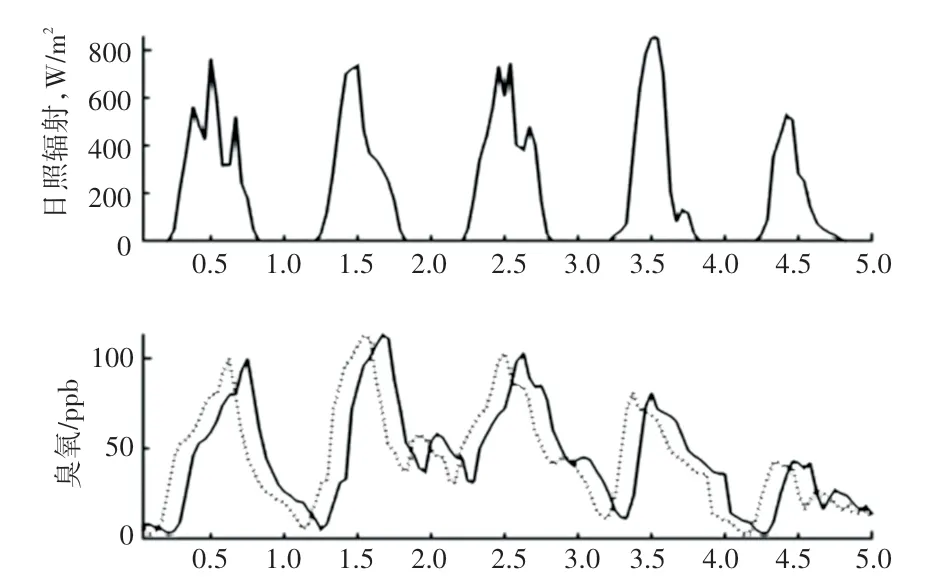
图6 时序滞后3 d 日照与臭氧相关图Fig.6 Correlation between sunshine and ozone with time lag of 3 d

滞后时间为3 d，日照与臭氧互相关性，如图7所示。 互相关系数达到了最大值，约为3.5×10。因为光照有一个过程，随着光照的增加，臭氧含量也逐渐增加到最大值，所以两者之间的相关函数也相应地呈现出最大值。

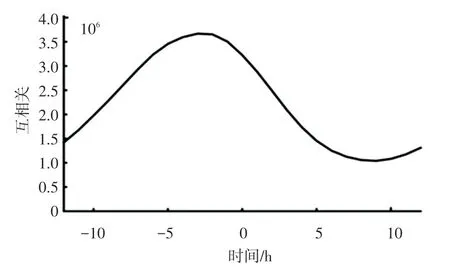
图7 日照与臭氧互相关性Fig.7 Cross correlation between sunshine and ozone content

5 结束语

在环境监测中，传感数据之间存在相关性，充分挖掘这些相关性，有助于分析影响环境的各种因素，从而准确、高效地采取措施。 这些相关性方法，还可以广泛应用在灾害预测等方面。 本文利用协方差分析变量之间的相关性，对PM2.5 指数、O浓度等与空气质量指数AQI 的相关性进行分析，得出PM2.5是主要影响因素，从而解决提升空气质量的问题；利用自相关系数在同一过程、不同时刻的相互关系，分析了北京市的PM2.5 的短期自相关性与长期自相关性，研究PM2.5 随时间情况；利用互相关函数来分析时间序列，对日照与臭氧之间的互相关性进行研究，结果说明，二者之间在一定时间间隔上存在相关性。 由于数据收集的局限性，本文数据样本还不够丰富，对一些相关性问题还需要数据样本的支撑。大数据时代的到来，数据相关性分析日益重要，下一步将考虑传感器网络中的数据补全等相关性问题，以进一步提高分析效率，节省传输能量。