ECP单轴受压本构关系及数值模拟

罗阳骁，田北平，李 俊，赵雅娜，易 兵

（四川轻化工大学a.材料科学与工程学院；b.土木工程学院，四川 自贡 643000）

引 言

ECP 可以满足我国目前建筑市场的需求[1]。对于这种新型建筑材料，材料本构关系的选取对于其结构分析结果的准确性和合理性有关键性作用，因而将对ECP单轴受压本构关系进行探索分析。

近年来，在国内外的研究中关于ECP 本构模型的研究鲜有报道，因此本文参考了相关复合材料的文献资料对其进行探索。HAN 等[2]提出了双折线本构模型，应力-应变关系上升段和下降段均采用斜直线表示，该模型虽然表达简单，但未考虑材料的残余应力，模型与试验结果的对比存在一定差异。

此外，多数国外研究更倾向于采用有理分式描述材料本构关系，翁婉琳[3]归纳了多位国外学者提出的有理分式。国内也有学者参考国外有理分式，在纤维混凝土、纤维水泥等材料的本构关系上进行探索。例如李艳[4]采用单轴受压试验，经过数学推导给出了新的有理分式，并且对待定参数的物理意义进行了阐述。

我国最常见的本构关系是过镇海模型[5]，与国外不同的是，过镇海模型采用的连续分段函数表示（曲线上升阶段为多项式，下降阶段为有理分式）。过镇海模型也常被许多研究者运用在纤维水泥基复合材料的本构关系拟合中。刘雁宁等[6]通过对不同纤维掺量的PVA-钢纤维混掺水泥基棱柱体进行单轴抗压试验，测得了纤维增强水泥基复合材料的应力-应变曲线试验数据，提出了拟合度较高的单轴受压本构模型。黄可等[7]对不同尺寸的高韧性聚乙烯醇增强水泥基材料进行了单轴抗压试验，分析了该材料抗压强度尺寸效应，并根据实测的应力-应变曲线提出了单轴受压本构模型。

在ABAQUS 自带的材料本构模型中，混凝土损伤塑性模型（CDP，concrete damage plasticity）在混凝土及类混凝土材料结构性能分析上应用广泛。国内学者大多根据《混凝土结构设计规范》GB 50010-2010[8]给出的混凝土本构关系推算CDP 模型相关参数。例如刘巍等[9]根据该规范中的本构关系，引入损伤因子，研究了CDP 模型中的参数设置并进行了验证。张劲等[10]通过规范中的混凝土本构关系，计算了CDP 中的损伤参数，并验证了其可靠性。杨霞等[11]用4 种不同方法计算了混凝土的损伤因子，并以剪力墙为例对比了不同的计算结果对模拟的影响，为后续剪力墙抗震性能模拟分析提供了理论依据。

综合上述文献研究成果可见，多数研究者的纤维水泥基复合材料本构关系运用在结构分析上，却不一定都能与试验结果相吻合。基于此，本文对ECP 进行单轴受压试验研究，在拟合适用于ECP 的单轴受压本构曲线的基础上，引入损伤，提出ECP在CDP 中的相关参数计算方法。采用试验和ABAQUS 模拟相结合的办法验证拟合曲线的可靠性，为后续ECP结构分析提供理论参考。

1 单轴抗压试验

1.1 试验原材料及试件制备

1.1.1 试验原材料

胶凝材料：P.O 42.5 普通硅酸盐水泥；磷石膏矿渣取自四川省德阳市什邡市；水泥和磷石膏矿渣主要化学成分见表1，试验配比见表2。增强纤维：河北廊坊盛拓保温材料有限公司生产的长度6 mm 聚丙烯纤维，抗拉强度为450 MPa，断裂伸长率为26.8%，弹性模量3.5 GPa；增塑剂：上海臣启化工有限公司生产的羟丙基甲基纤维素，10 万粘度；减水剂：上海臣启化工有限公司生产的聚醚羧酸减水剂，灰白色，含水率为1.81%。

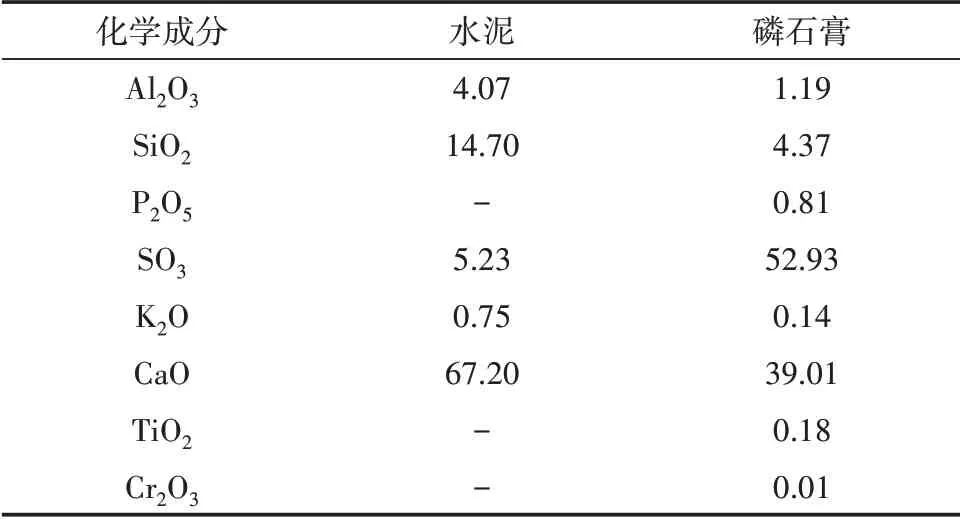
表1 水泥、磷石膏矿渣主要化学成分 %

表2 配合比设计 %

1.1.2 试件制备

本文试验参考市场工艺[12]进行试件的制备：先将原料（水泥、磷石膏）和纤维（聚丙烯纤维）放入高速混料机内预混合2 min，然后加水和外加剂（HPMC、聚醚羧酸），再混合3 min，之后将搅拌均匀的混合料输送进挤出机进行真空挤出成型。

挤出成型后，将挤出板切割成五块立方体试件（100 mm×100 mm×100 mm）。切割后，将试块进行编号,分别记作T1、T2、T3、T4、T5，在22 ℃、95%相对湿度下静置8 h，然后在60 ℃下进行蒸汽养护16 h，再于22 °C 和50%相对湿度下将挤出制品保存14 d，最后开始试验测试。制备路线如图1所示。

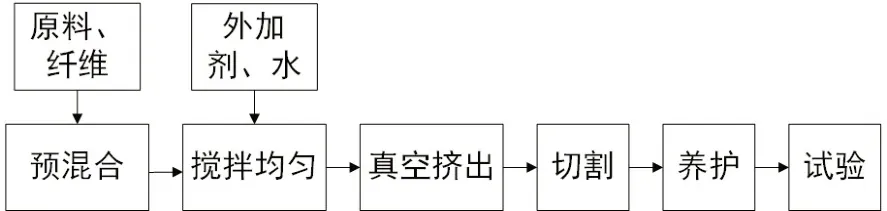
图1 制备路线

1.2 试验方法

养护完成后，取出试件，将试件表面擦干净并进行找平处理，试件承压面选取成型时的侧面，试件中心正对于试验机的下压板中心，以保证安装到试验机的下压板后，试件处于水平状态；试验过程中连续均匀地加载，加载方式采用位移加载（加载速率为0.5 mm/s），直到试件被破坏，记录破坏荷载。

1.3 试验结果

1.3.1 试验现象

ECP 单轴受压试验加载过程可分为以下几个阶段：

（1）接触阶段：这个阶段试件从零开始缓慢加载，试件受压面与试验机上压板开始接触，并且受压表面有些许剥落现象，试件整体并没有明显的变化，荷载缓慢上升，荷载位移曲线平缓上升，曲线斜率较小。

（2）弹性阶段：试件受压面与试验机上压板完全接触，试件整体没有出现明显裂缝,荷载与位移曲线按一定斜率增长，近似呈线弹性关系。

（3）塑性阶段：试件表面开始出现裂缝,试件也开始发生破坏，整体并没有完全断裂，由于纤维限制了裂缝的发展，能够听到细小的撕裂声音。该阶段曲线斜率比弹性阶段小且在慢慢变小，曲线增长较为缓慢。

（4）破环阶段：ECP试件破坏时并没有突然断裂破坏，而是裂缝逐渐贯通试件，当裂缝贯通试件时终止试验。曲线达到峰值，开始缓慢卸载，曲线开始下降，表面无外鼓和明显剥落现象，整个受压过程保持了良好的整体性，说明试件基体有良好的韧性，试件破坏形态如图2所示。

1.3.2抗压强度

试验得到5 组100 mm 立方体的破坏荷载，抗压强度根据式（1）计算：

式中：fcc为立方体抗压强度，MPa；Fcc为试件破坏荷载，N；Acc为试件承压面积，mm2。各试件试验结果见表3，各试件荷载-位移曲线如图3所示。

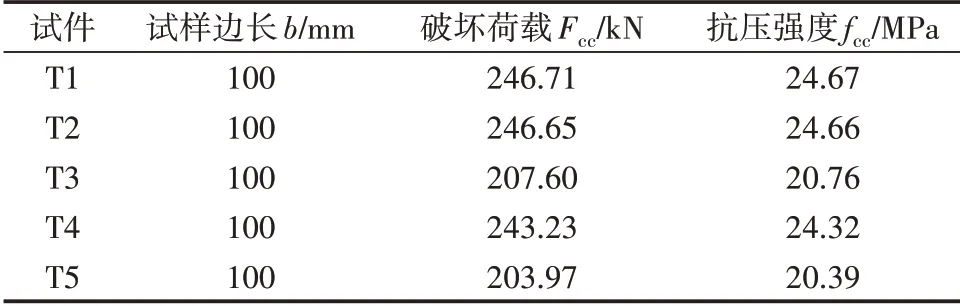
表3 立方体抗压强度

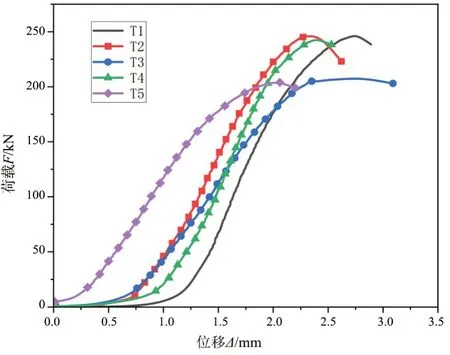
图3 ECP单轴受压荷载-位移曲线

由于T3 与T5 试块的切割部位与T1、T2、T4 不同，试验强度相差较大，为了使后续拟合更精确，本文采用T1、T2、T4 的实验结果作为计算依据。取T1、T2、T4试验结果的平均值24.55 MPa作为ECP的立方体强度值。经过试验数据处理，得到各试块的应力-应变曲线如图4所示。

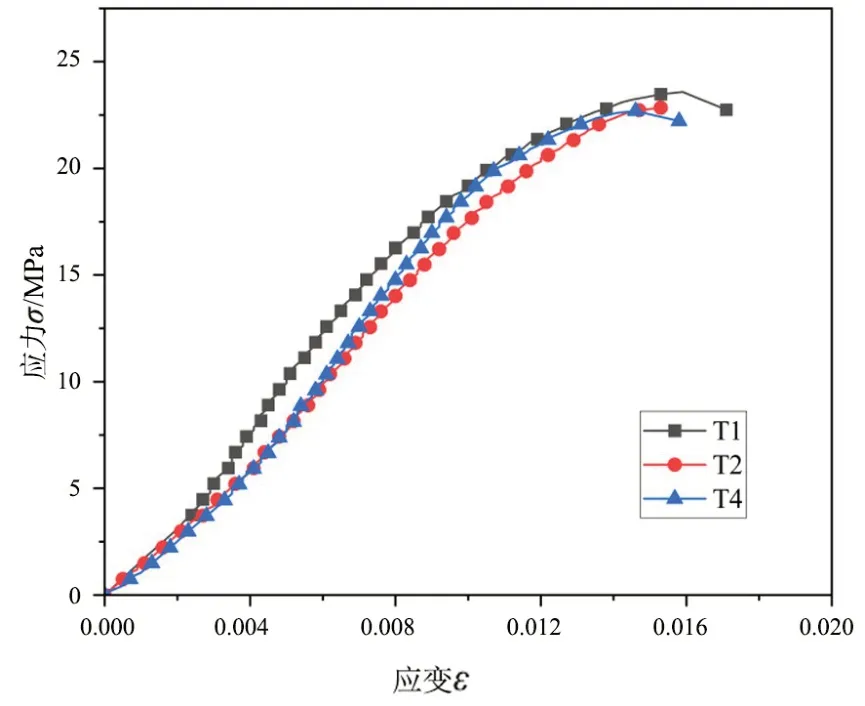
图4 T1、T2、T4受压试验应力-应变曲线

2 本构关系

2.1 拟合方程

对于非线性分析本构模型，本文为方便进行非线性拟合，首先将试验所得应力、应变值采用归一化处理，以无量纲表示 ，将归一化处理后的无量纲数值分别记为x、y，具体归一化处理方式如下：

式中：σ为试验所得应力值，ε为试验所得应变；σcu为峰值应力；εcu为峰值应力对应的应变。

将试验值根据式（2）处理后，峰值点坐标设置为（1,1）。根据图4 中的试验曲线以及试件各阶段的受力特点，用归一化后的无量纲数值进行拟合，得到ECP单轴受压应力-应变曲线如图5所示。

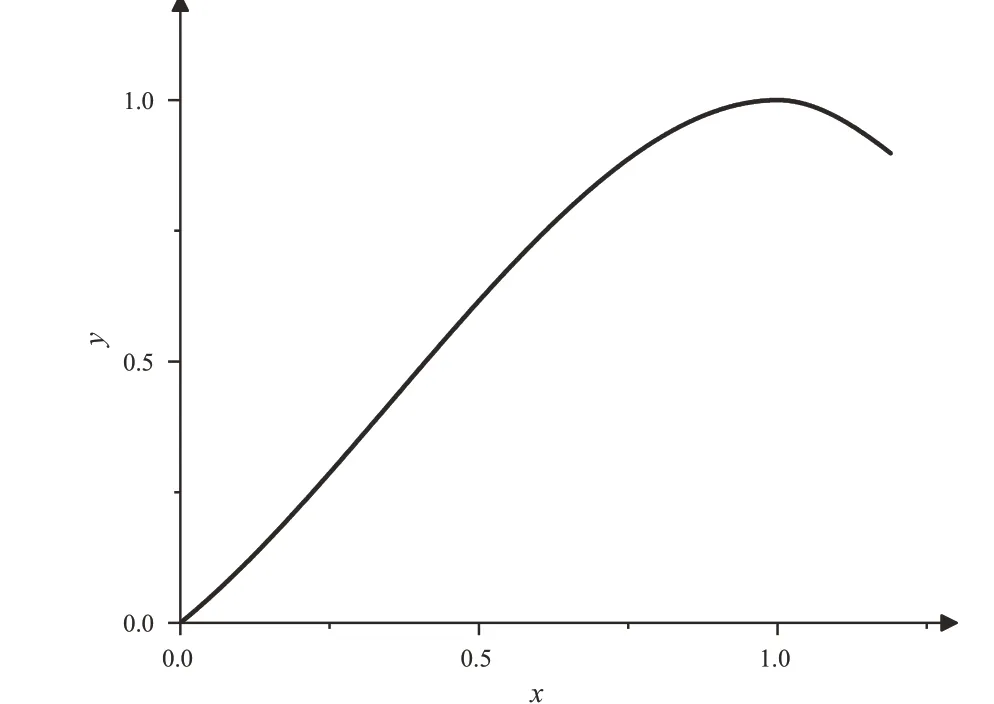
图5 ECP单轴受压应力-应变曲线（归一化）

由图5 可知，ECP 受压应力-应变曲线具有以下特点：

（1）x= 0，y= 0；

（2）0 ≤x≤1，曲线呈上升阶段；

（3）x= 1，曲线达到峰值；

（4）x＞1，曲线下降；

（5）归一化全曲线，x≥0，0 ≤y≤1；

确定适用于ECP 受压应力-应变关系的数学方程如下：

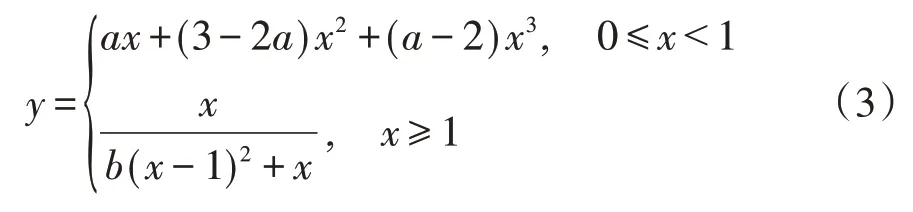
利用非线性回归分析方法将试验数据代入方程进行拟合，确定方程中的未知参数。拟合结果如图6 所示，图中可见拟合曲线与各试验曲线吻合良好。

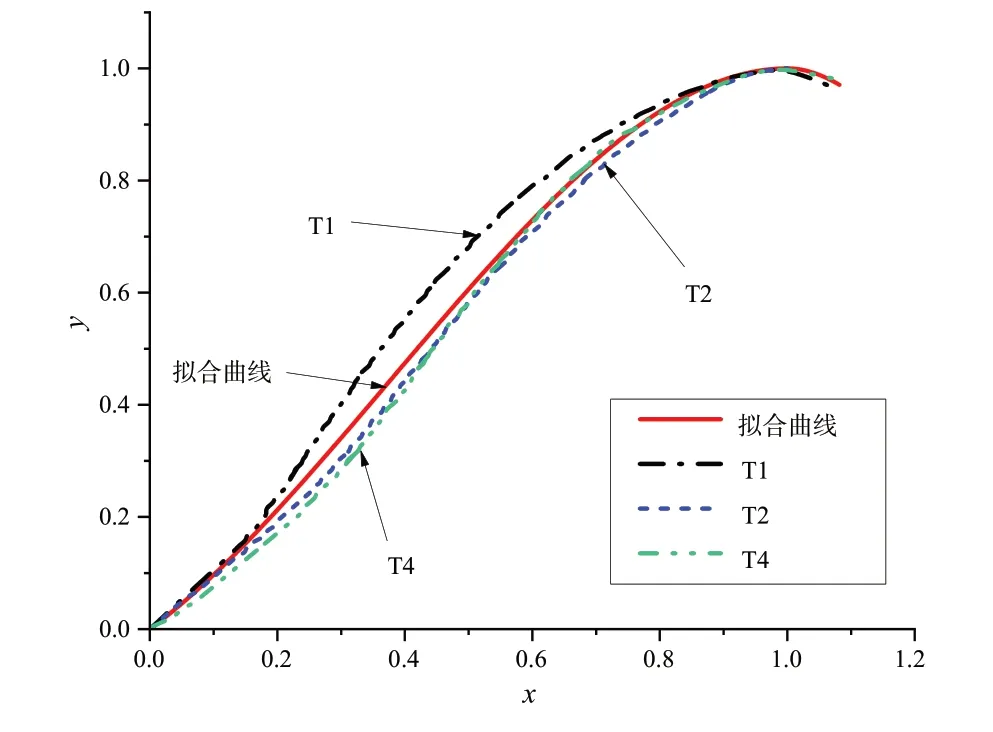
图6 拟合曲线与试验曲线比较

2.2 待定系数

采用最小二乘法对试验数据进行非线性回归，得到试件受压应力-应变曲线函数表达式的待定系数a、b的取值以及拟合后的确定系数R2，见表4。表4中可见，R2趋近于1，表明拟合吻合度较高。

表4 系数a、b和R2的取值

3 CDP参数计算

3.1 损伤模型的应力-应变参数计算

ECP损伤塑性模型如图7所示。

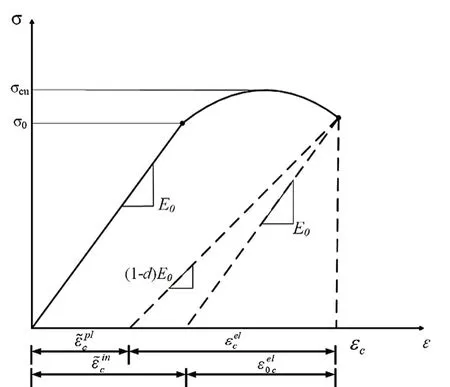
图7 ECP损伤塑性模型

图7 中，dc为压缩损伤因子；E0为初始弹性模量；为非弹性压缩应变；为压缩等效塑性应变；为无损状态下的弹性压应变；为可恢复的弹性压应变。

由于试验所得均为名义应力和名义应变，在ABAQUS损伤塑性模型中，需要输入的是真实应力、真实应变值。因此，在进行模拟前需要对试验数据进行转换，应力-应变转换公式如下：

式中：σt、εt分别为真实应力、真实应变；σn、εn分别为名义应力、名义应变。

另外，在CDP 模型中，材料的受压行为通常通过单轴受压下的非弹性压缩应变（）进行计算。根据图7 中各应变之间的关系，非弹性压缩应变等于总压缩应变（εc）减去弹性压应变：

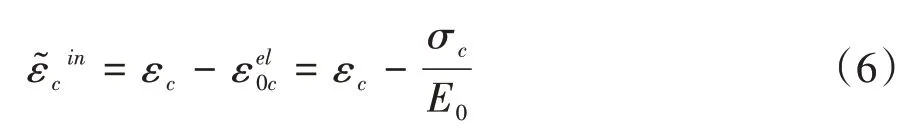
以本文的室内试验为例，通过试验数据可以得到ECP材料压缩真实应力-非弹性应变见表5。

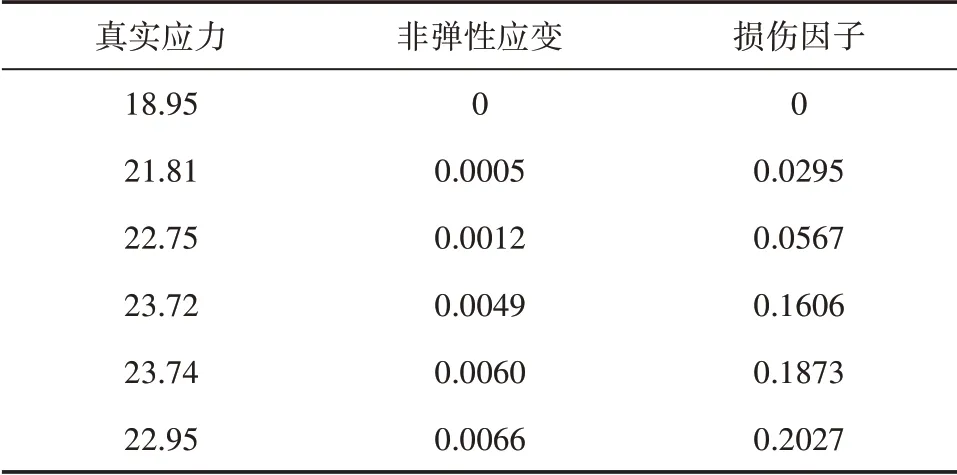
表5 受压损伤参数

3.2 损伤因子计算

ABAQUS混凝土损伤塑性模型中的损伤即材料内部凝聚力在载荷作用下进展性地减弱，使受载材料产生缺陷裂纹与微孔[19],但是损伤状态难以通过试验进行测定，CDP 模型就引入了损伤因子的概念来描述损伤。相关研究中引入了Sidiroff 理论[20]，该理论假设受损材料与无损材料产生的弹性余能在形式上相同。

无损材料弹性余能（）表示为：

有损材料弹性余能（）表示为：

其中：ED为损伤时的弹性模量，σˉ为等效应力。σˉ根据下式计算：

根据理论可以推导出，损伤时的弹性模量（ED）：

进而得到材料的应力-应变关系式：

再结合式（2）～（3）可以得到ECP 压缩损伤因子dc计算式：

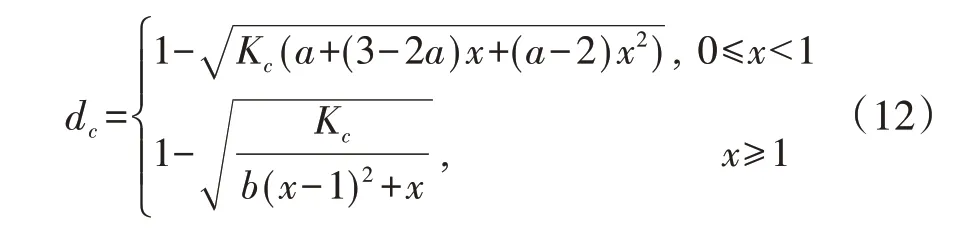
4 算例验证

将拟合得到的各计算参数代入ABAQUS 进行数值模拟分析。本节算例模拟上述受压试验，以验证CDP参数计算的正确性。

首先分别建立ECP 立方体试块和上下施压钢板，模型几何尺寸与试验一致。定义材料属性具体数值参照计算结果见表5。

选择通用静力分析，ECP 与两块钢板之间采用Tie 约束，使其与钢板不产生相对运动；上钢板定义一个参考点RP-1 与之进行耦合（Coupling）,使得上端钢板相对于RP-1 呈刚体运动；下钢板定义完全固定；采用位移加载模拟整个试验，为了使得模拟结果较为可靠，加载制度与试验一致，通过Amplitudes 控制加载速率；全局采用六面体网格划分。试件加载方式及网格划分如图8所示。

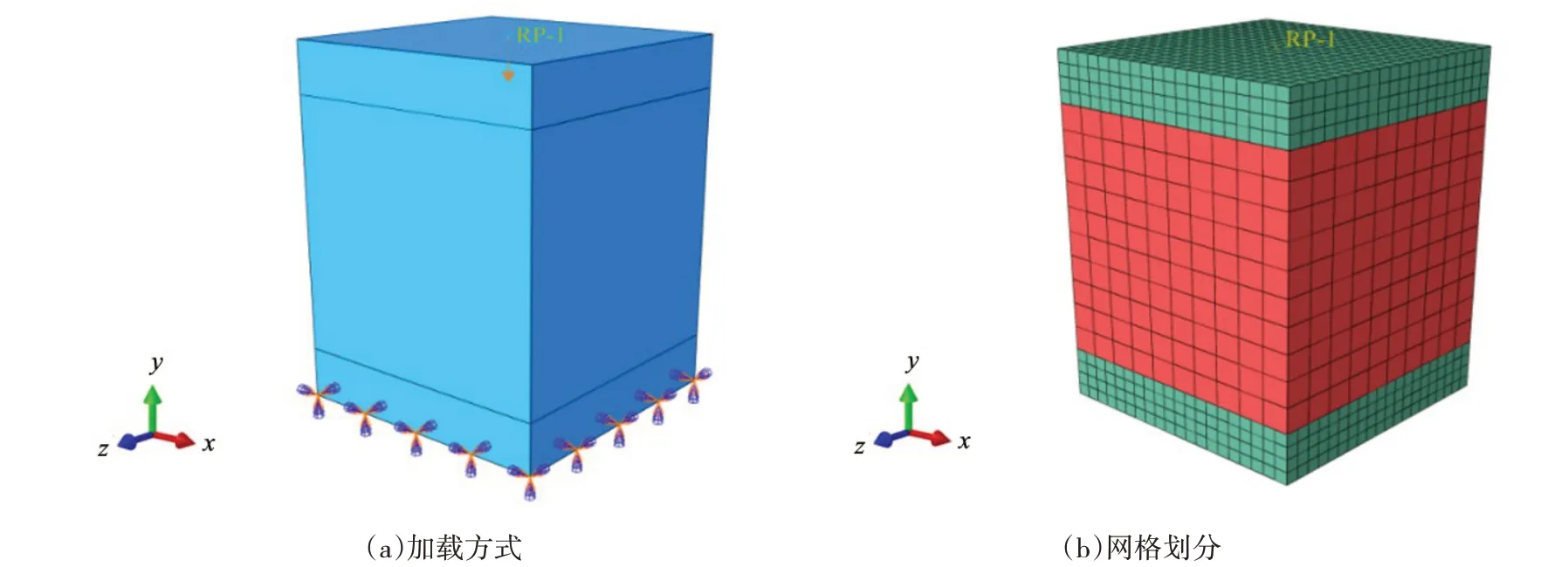
图8 试件加载方式和网格划分

计算完成后进入可视化板块（Visualization）观察分析结果。图9 所示为ECP 压缩损伤云图，图中可见，在加载结束后最大压缩损失值为0.2027，这与理论计算结果基本相近，且损伤在中心单元附近达到最大。

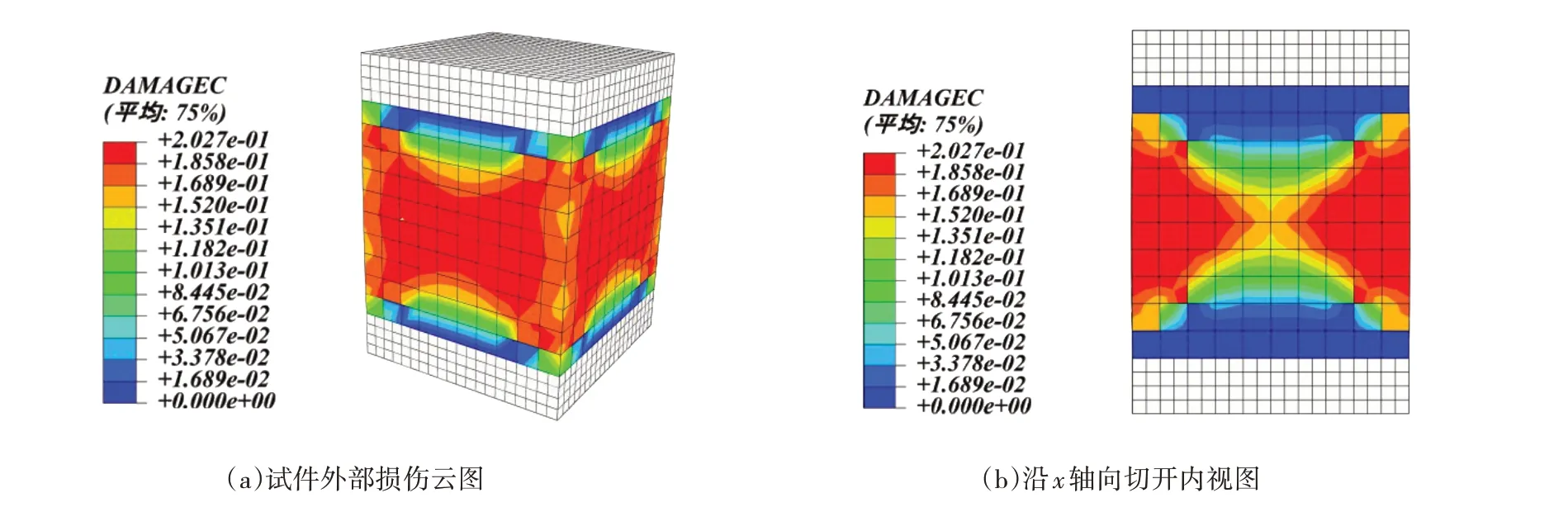
图9 ECP损伤云图

图10（a）所示为试件最大塑性应变符号图，可见试件最大塑性应变与最大应力方向一致，受压缩作用；图10（b）所示为最小塑性应变符号图，箭头指向为裂缝可能出现的方向，这与试验现象相符，说明该计算结果相对可靠。

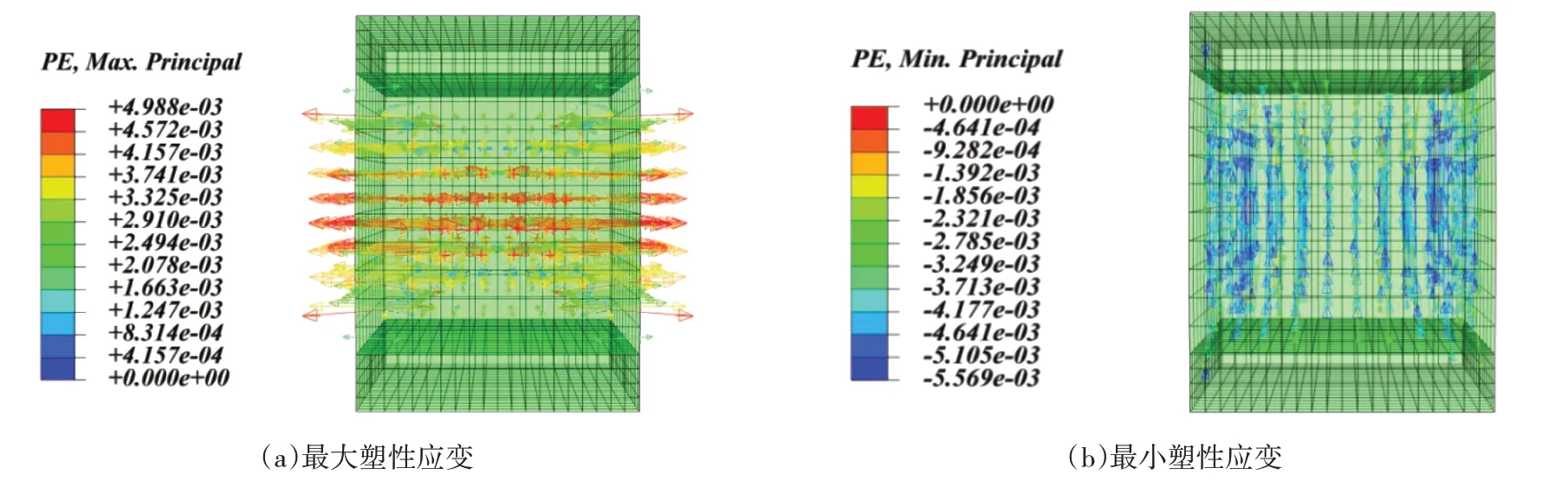
图10 塑性应变符号图

图11 所示为试验和模拟应力-应变曲线对比图，整体曲线趋势相近，模拟计算的峰值应力为26.28 MPa，试验组峰值应力平均值约为24.55 MPa，相对误差约为1.83%；计算峰值应变为0.0154，试验组峰值应变平均值约为0.0156，相对误差为1.28%，误差均在2%之内。由此可见，有限元计算结果与试验结果基本吻合，进一步验证了本文所建立的ECP单轴受压本构模型的正确性。

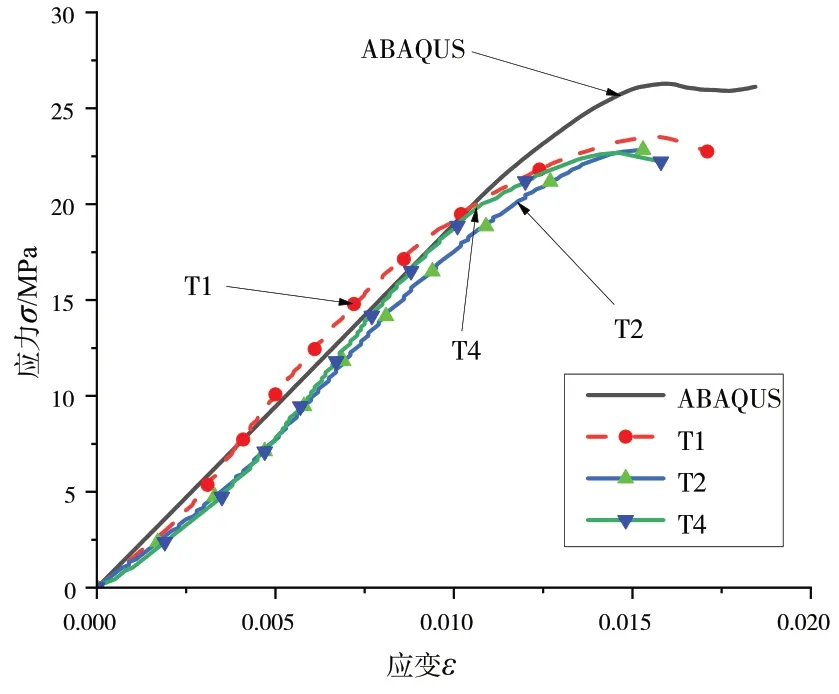
图11 应力-应变曲线对比

5 结 论

通过单轴受压试验和数值模拟相结合的方式分析了ECP 在单轴受压情况下的本构关系，主要结论如下：

（1）基于单轴抗压试验得到的应力-应变数据，得到了适用于真空挤出成型纤维增强水泥墙板材料的单轴受压本构模型。与试验数据的对比分析表明，提出的本构模型可以较好地预测该材料的单轴抗压行为，且根据本构曲线特征和数学推导，本文给出了相关参数的物理意义。

（2）根据Sidoroff 提出的能量等价原理，将试验所得本构关系转换为ABAQUS 中的CDP 模型，计算得到损伤因子，模拟了受压试验。从模拟所得压缩损伤云图、等效塑性应变云图以及最大（最小）塑性应变符号图来看，都与试验破坏形式相符，说明了该模型的正确性。

（3）模拟所得应力-应变曲线与试验应力-应变曲线整体趋势相近，但计算峰值应力比试验峰值应力高出约1.1 MPa，计算峰值应变比试验应变小0.0002，两者相对误差均控制在2%以内，说明CDP模型能较好地适用于ECP材料。