复杂轮轨接触条件下机车牵引/制动性能分析

李 伟，郭欣茹，裴志远，宋洪锐，胡彦霖，凌 亮

（1.中铁二院工程集团有限责任公司，成都 610031；2.西南交通大学牵引动力国家重点实验室，成都 610031）

引 言

列车的牵引力和制动力均通过轮轨滚动接触界面来传递，而轮轨黏着决定着牵引力和制动力的上限[1]。在实际运营中，复杂多变的运行环境会使机车面临更加恶劣的轮轨接触条件，尤其在雨雪天气下轨面黏着系数会明显下降，从而导致机车出现踏面剥离等车轮损伤情况[2-3]。

国内外专家对不同运行工况下列车的轮轨黏着特性开展了大量的研究工作。CHANG 等[4]通过试验台研究了喷水量、轮轨接触表面粗糙度、运行速度、水温和轴重等因素对轮轨黏着系数的影响。黄万亮等[5]通过试验发现，在干态、水介质和防冻液介质影响下，坡道工况下的轮轨黏着系数低于平直道工况。王文建等[6-8]研究发现，与干燥状态相比，湿润、油态等低黏着工况不仅会导致黏着系数明显降低，还会使轮轨黏着-蠕滑曲线峰值点发生左移。吴兵等[9-11]建立了考虑热效应、轮轨表面微观粗糙度和界面污染物的轮轨黏着数值分析模型，通过理论分析了不同速度、轴重、表面粗糙度和温度条件下的轮轨黏着特性。

目前已有的研究工作主要关注轮轨间存在“第三介质”时对黏着系数的影响，而对复杂轮轨接触条件下列车牵引制动性能的研究较少。实质上列车牵引或制动性能的发挥效果依赖于轮轨间的黏着特性[12]，在低黏着接触状态下，可能会出现黏着力小于列车牵引力或制动力的情况，导致车轮空转或车轮打滑，对列车牵引和制动能力的发挥有较大影响[13]。尤其在高寒山区长大坡道线路上，当机车发生车轮空转或打滑时甚至会出现无法控制列车速度的危险情况[14]。因此，研究复杂轮轨接触条件下列车在长大坡道上运行时的牵引/制动性能，对保障行车安全，降低轮轨损伤，以及列车驾驶和操纵优化方面都具有积极的意义。

首先通过建立列车-轨道动力学模型分析10‰～30‰坡道下不同轮轨接触条件对轮轨黏着情况的影响，然后计算了货物列车在低黏着条件下为保证列车牵引/制动特性正常发挥所能够施加的最大牵引/制动力，并给出了低黏着条件下建议采用的牵引/制动特性曲线。

1 动力学仿真模型

为分析复杂轮轨接触条件下轮轨间的黏着特性，基于车辆-轨道耦合动力学理论[15]，建立了货物列车-轨道垂纵动力学模型。图1 所示为动力学模型及车体受力图，列车-轨道垂纵动力学模型主要包括货物列车模型、有砟轨道系统模型、防滑控制模型和列车纵向力计算模型。其中，货物列车模型编组考虑为HXD2双机牵引2000 t 货物列车。列车纵向力计算模型展示了单节车车体受力情况。图1中，α为第i节车所处线路断面的坡度，Fci-1和Fci分别为第i节车的前后车钩力，Fwi为第i节车的运行阻力（坡道阻力和列车基本运行阻力之和）。

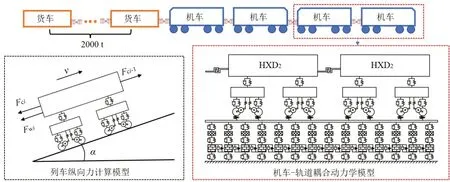
图1 列车-轨道垂纵动力学模型及车体受力示意图

1.1 货物列车和有砟轨道系统动力学模型

动力学仿真模型中，每节HXD2型机车包含1个车体、2 个构架、2 个牵引拉杆、4 个轮对以及4 个牵引电机，每个部件考虑纵向、垂向、点头3 个方向自由度。由于对列车牵引/制动性能的研究重点关注机车的黏着特性，因此为简化计算，将编组中20 节货车视为单质点模型，仅考虑其纵向自由度。货物列车系统的动力学响应求解方程可表示为：

式中：ML、CL和KL分别为列车系统的广义质量矩阵、广义阻尼矩阵和广义刚度矩阵；xL为列车系统的广义位移矢量；FL为列车系统所受外力载荷矢量。有砟轨道系统模型由钢轨、扣件、轨枕、道床和路基组成。其中，钢轨考虑垂向振动，采用连续弹性离散点支撑的欧拉梁模型模拟；扣件系统采用弹簧-阻尼单元模拟；轨枕和道床块均采用刚性体模拟，且忽略路基的振动响应。轨道系统模型各构件均考虑其垂向振动。钢轨的垂向振动微分方程如下[15]：

式中：Zr(x,t)为钢轨的振动位移变量，E为钢轨的弹性模量；IY为钢轨截面对Y轴的转动惯量；Frsi和Fnj分别为第i个扣件（i= 1,…,N）和第j位车轮（j=1,2,3,4）对钢轨的垂向作用力；x为钢轨坐标系纵向坐标；xi和xwj分别为第i个扣件和第j位车轮对应纵向坐标；δ为狄拉克函数。

货物列车和轨道系统动力学响应通过翟方法进行积分求解，其积分形式如下[15]：

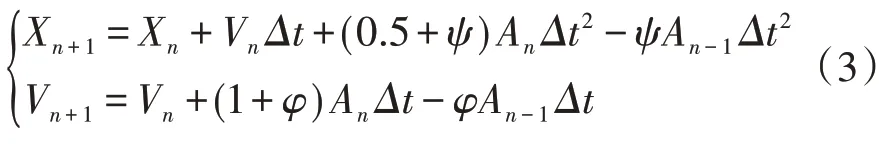
式中：X、V和A分别为系统位移、速度和加速度响应；Δt为时间积分步长；φ和ψ为控制积分方法特性的独立参数；下标n、n- 1 和n+ 1 分别为当前积分步时刻、上一步和下一步时刻。

轮轨滚动接触模型中，通过赫兹接触理论计算轮轨法向力Fz，在轮轨纵向蠕滑力Fcreep的求解中应用Polach滚动接触理论[16-17]，其表达式如下：

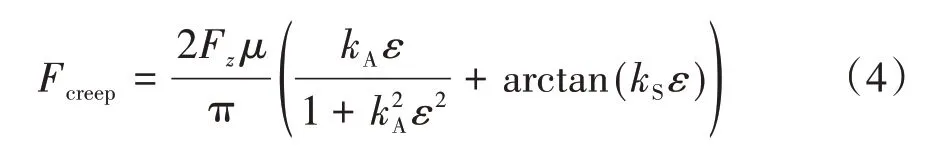
式中：ε= 2Cπa2bsx/3Fz μ，μ为变摩擦系数，kA、kS分别为接触斑粘着区、滑移区缩减系数，C为表征接触剪切刚度的比例系数，a和b分别为接触斑长短半轴，sx为轮轨纵向蠕滑率。

由于不同轮轨相对滑动量和接触条件对轮轨黏着特性的影响显著，在求解轮轨蠕滑力时采用了变摩擦系数模型，以描述机车在不同接触状态下的黏着特性。变摩擦系数μ通过下式计算[16]：

式中：μ0为静滑动摩擦系数，w为相对滑动速度大小，A为滑动速度无穷大时的摩擦系数μ∞与静滑动摩擦系数μ0之比，B为摩擦力衰减系数。针对典型气候条件下轨面摩擦系数的改变，仿真计算中分别考虑了“干燥”、“湿润”、“油态”、“冰雪”4 种轮轨表面接触状态对轮轨黏着的影响，具体相关参数见表1。采用变摩擦系数模型可以求解得到不同接触状态和纵向蠕滑率下的轮轨纵向蠕滑力Fcreep，从而得到黏着特性曲线如图2 所示，图中颜色不同的实线代表不同轮轨接触条件下的黏着系数f，黏着系数f的计算方法为纵向轮轨蠕滑力Fcreep与轮轨法向力Fz之比值；与实线颜色相同的虚线代表同一接触条件下的变摩擦系数μ。

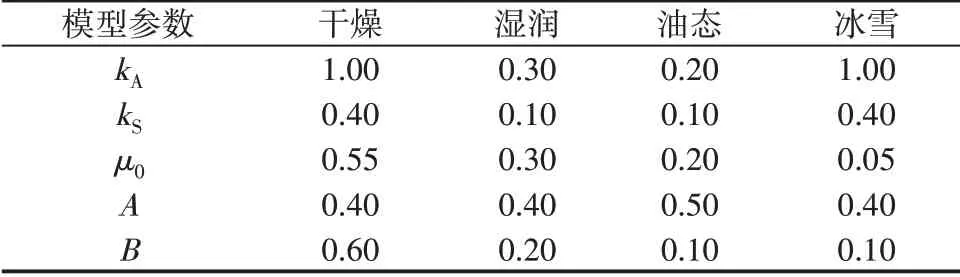
表1 轮轨接触条件参数[18-19]

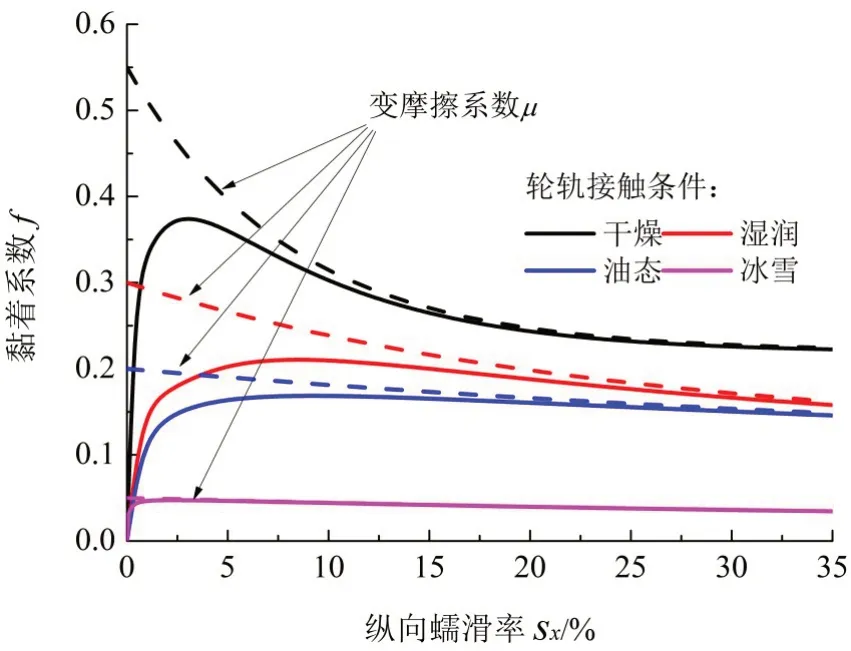
图2 不同接触条件下轮轨黏着特性曲线

1.2 防滑控制模型

传统防滑控制一般将机车车轮速度差、加速度或滑行率作为车轮打滑的判定依据。当检测到机车车轮的速度差、加速度或滑行率超过设定阈值时，则判定发生空转或打滑，防滑控制器开始动作并执行力矩卸载、维持、恢复等过程以恢复黏着[1]。本文仿真模型采用PI 控制模型[20]模拟防滑控制器，机车模型中每个轮对拥有独立的防滑控制器。通过计算出当前的滑行率并与控制阈值进行比较，以判断车轮是否发生空转或打滑。若车轮滑行率低于阈值则防滑控制器不被触发，否则防滑控制器触发，并对输出的转矩进行调整。本文防滑控制器模型的控制阈值设置为0.03。

1.3 列车纵向力计算模型

根据图1中的第i节车车体纵向受力图可知，每节车纵向受力包括前后车钩力Fci-1、Fci以及运行阻力Fwi，其中运行阻力Fwi求解方式如下：

要提升牛羊口蹄疫防治工作的质量，首先应该在养殖户较多的地区充分进行疫情的排查，尤其是对于牛羊养殖密集的养殖区、牛羊交易市场等地区进行严密的疫情排查。通过将兽医进行分组，并以小组为单位划分排查区域，从而保证排查工作的规范和效率，在进行排查的过程中，工作人员应该认真细致的进行排查，最大程度的消除牛羊口蹄疫的隐患。

式中：Mi为第i节车的质量，w″0为车辆的单位基本运行阻力，每节机车单位基本运行阻力为[21]：

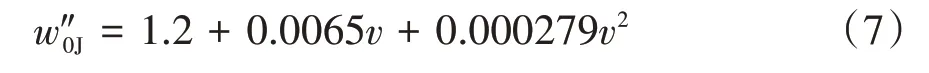
式中：v为列车运行速度，km/h。每节货车单位基本运行阻力为[21]：

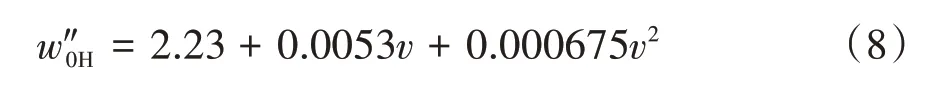
列车在坡道上运行时，坡道阻力和基本运行阻力作用于各车体质心。需要说明的是，为对比不同坡度对列车轮轨黏着特性的影响，仿真计算中列车在不同坡度的坡道下均保持相同速度匀速运行，因此需要在机车上施加与整列车坡道阻力相当大小的牵引或制动力，并以力矩的形式施加于每个轮对的车轮中心。

2 长大坡道动力学仿真分析

为对比货物列车在复杂运营环境、不同坡度长大坡道下运行时的轮轨黏着情况，利用上述列车-轨道耦合模型进行仿真计算。由于列车在牵引上坡和制动下坡时，同样大小的牵引力或制动力对轮轨黏着特性的影响规律类似，因此仅以牵引上坡工况为例，对比分析了10‰、20‰、30‰坡度下轮轨法向力、纵向蠕滑率和黏着系数的动态响应。仿真计算中货物列车上坡运行速度均为75 km/h。运行线路中200～650 m 区段为低黏着接触条件，其中200～250 m 区段为湿润接触条件，250～400 m 区段为油态接触条件，400～650 m区段为冰雪接触条件。

图3 所示分别为10‰、20‰和30‰坡度牵引上坡工况下机车4 个轮对的轮轨法向力，图中可以看出，牵引力的施加导致了轴重转移现象，其中一位和二位轮对减载，三位和四位轮对增载。随着坡度增加，牵引力增大，机车的轴重转移量也随之增大。

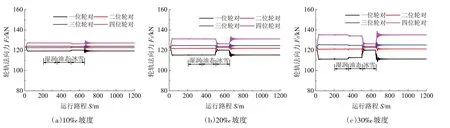
图3 牵引上坡工况轮轨法向力

图4 所示为不同坡度下4 个轮对的轮轨纵向蠕滑率动态变化情况，图中可以看出，随着坡度的增大，轮轨纵向蠕滑率增大。不同的轮轨表面接触状态对轮轨的蠕滑行为影响显著，当坡度为10‰时，轮轨纵向蠕滑率在经过湿润、油态、冰雪区域过程中依次增大，而在冰雪接触区域内4 个轮对均发生了车轮空转现象，此时纵向蠕滑率突然增大，防滑控制器被触发，从而使得轮轨纵向蠕滑率维持在3%（控制阈值）附近。当坡度为20‰时，纵向蠕滑率有所增大，且仅在冰雪区域内发生了车轮空转。当坡度为30‰时，受牵引载荷增大的影响，4个轮对在油态和冰雪区域内均出现了空转现象，而湿润接触状态未引起车轮空转。

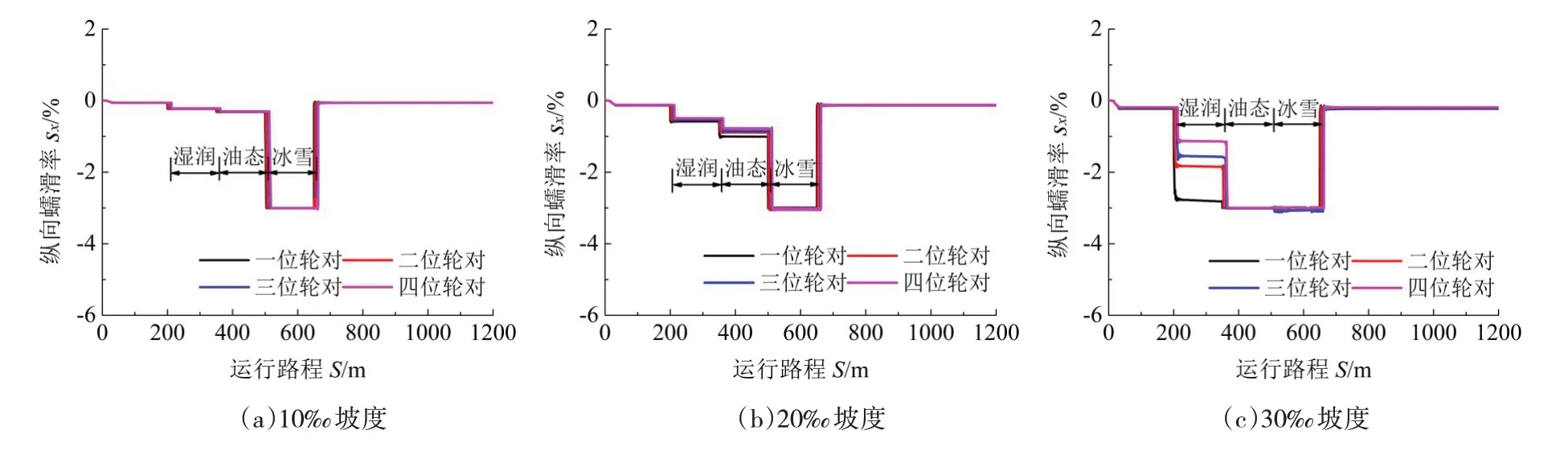
图4 牵引上坡工况纵向蠕滑率

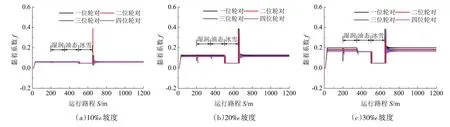
图5 牵引上坡工况黏着系数

3 复杂轮轨接触条件下牵引制动能力分析

机车的黏着特性曲线在各种接触条件下都存在相应的黏着峰值点（图2），即在该点处所能提供的摩擦力最大[8]。因此在不同的轮轨接触条件和不同运行速度下，轮轨间蠕滑率存在一个限值，当在轮对上施加过大的牵引力或制动力时，轮轨蠕滑率会超过该限值，导致车轮发生打滑或空转，该蠕滑率所对应的黏着系数则为该运行条件下黏着系数的最大值，由此可计算得出该运行条件下机车能够正常发挥的最大牵引力或制动力。本小节对货物列车在干燥、湿润、油态和冰雪接触条件下能够施加的最大牵引/制动力进行了计算，并给出了在低黏着条件下建议采用的牵引/制动特性曲线。

图6所示为货物列车在不同接触条件下为保证列车牵引/制动特性正常发挥所能够施加的最大牵引/制动力，其中虚线为计算得到的最大牵引/制动力结果；实线为HXD2型机车现采用的牵引/制动特性曲线，即牵引力和制动力的上限值。计算结果表明，货物列车可施加的最大牵引/制动力随着运行速度增加而减小。干燥接触状态下货物列车所能够施加的牵引/制动力最大，且均大于HXD2型机车的牵引力和制动力上限值，这说明在良好的轮轨接触状态下，货物列车现有的牵引特性曲线可以保证列车牵引/制动特性得到正常发挥。随着轮轨接触条件的恶化，由于黏着系数降低，在湿润、油态和冰雪接触条件下的最大牵引/制动力值依次降低且低于HXD2型机车牵引力和制动力上限值。为避免货物列车在牵引/制动过程中出现车轮空转/打滑，建议在低黏着接触条件下适当降低牵引力和制动力。

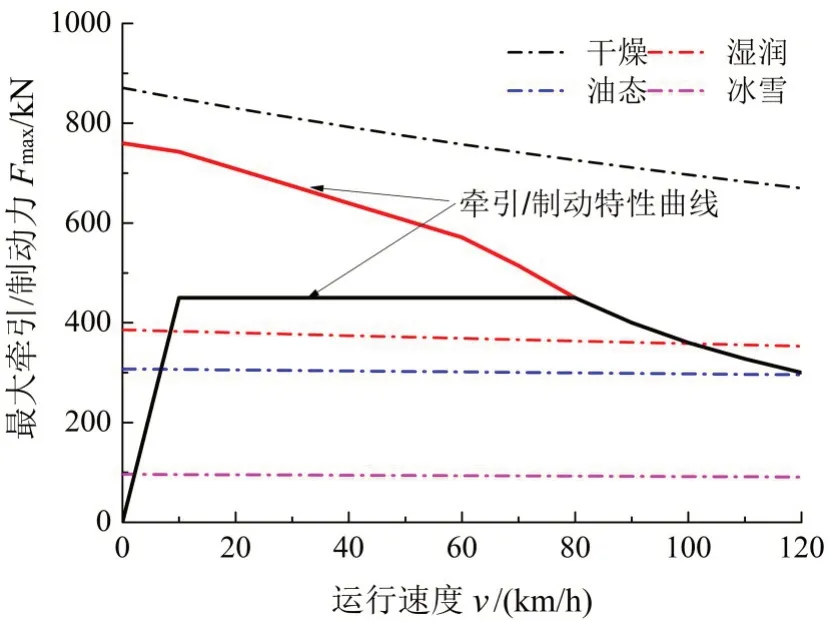
图6 货物列车可施加的最大牵引/制动力

图7 所示为货物列车在不同接触条件下的牵引/制动特性曲线。值得注意的是，在干燥轮轨接触状态下，列车现有的牵引/制动特性可以正常发挥，而在湿润、油态和冰雪接触条件下牵引力和制动力限值降低，因此根据不同的轮轨接触状态对机车现采用的牵引/制动特性曲线进行了调整。图7 中虚线标注了货物列车在10‰、20‰和30‰坡道下受到的阻力，牵引上坡时列车阻力为坡道阻力与基本运行阻力之和，制动下坡时列车阻力为坡道阻力与基本运行阻力之差。当某一坡度下的列车阻力和不同接触状态下牵引或制动力存在交点时，交点处所对应的运行速度为在此种运行工况下列车的最大匀速运行速度，即均衡速度；若某一坡度下列车阻力均高于列车牵引或制动力，说明在该坡度下列车无法保持匀速运行。从图7 中可以看出，当坡度为10‰和20‰时，坡道阻力低于干燥、湿润和油态接触条件下的牵引/制动力，表明在上述运行工况下列车牵引/制动力均能正常发挥并保持匀速运行；当坡度为30‰时，货物列车在油态和冰雪接触条件下均无法保持匀速运行，而在干燥和湿润状态下牵引能力正常发挥时的均衡速度为111 km/h。其中，在冰雪接触条件下，列车在10‰～30‰坡度运行时列车运行阻力均超过了列车能够发挥的最大牵引/制动力，因此在该坡度范围内的冰雪接触条件下列车无法保持匀速运行。

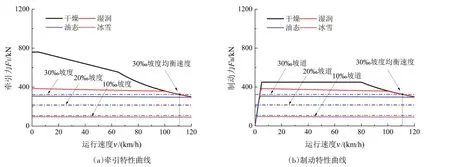
图7 货物列车不同接触条件下牵引/制动特性曲线

4 结 论

基于车辆-轨道耦合动力学理论，针对HXD2双机牵引2000 t 货物列车编组建立了列车-轨道垂纵动力学模型，对比分析了不同坡道、不同轮轨接触条件对机车轮轨法向力、纵向蠕滑率和黏着系数的影响；根据黏着特性曲线计算得到了不同轮轨黏着条件下能够发挥的最大牵引/制动力，并给出了在低黏着条件下建议采用的牵引/制动特性曲线，结论如下：

（1）货物列车在牵引状态匀速通过10‰和20‰坡道时，在冰雪接触状态下会发生车轮空转，通过30‰坡道时，在油态和冰雪接触状态下均会发生车轮空转。当出现车轮空转时，车轮纵向蠕滑率会明显增大，黏着系数会有所减小，且黏着系数会随着接触条件的恶化而降低。

（2）干燥接触状态下，HXD2型机车现有的牵引特性曲线可以保证列车牵引/制动特性正常发挥。在湿润、油态和冰雪接触条件下的最大牵引/制动力值依次降低且低于HXD2型机车牵引/制动力限值。因此，为避免在货物列车在牵引/制动过程中出现车轮空转或打滑，建议在低黏着接触条件下适当降低牵引力和制动力。

（3）在坡度超过10‰时的冰雪接触条件下，列车运行阻力均超过了列车能够发挥的最大牵引/制动力，因此在该坡度范围内的冰雪接触条件下列车无法保持匀速运行。当坡度为30‰时，货物列车在油态和冰雪接触条件下均无法保持匀速运行，而在干燥和湿润状态下牵引能力正常发挥时最大均衡速度为111 km/h。