腹板开孔冷弯卷边槽钢双肢拼合梁的畸变屈曲研究
2022-05-10赵笙惠孙家贤袁伟斌余南霆
赵笙惠,孙家贤,袁伟斌,余南霆
(浙江工业大学土木工程学院,杭州 310023)
引 言
工程上,随着冷弯型钢建筑结构层数的提高及为了满足一些构造要求,会将多个单肢冷弯卷边槽钢组合成多肢组合截面构件[1]。作为典型组合截面构件,腹板开孔冷弯薄壁卷边槽钢双肢组合式截面构件由自攻螺栓将两个单肢开孔冷弯卷边槽钢连接而成,其应用越来越广泛[2]。
在冷弯薄壁构件屈曲模式的研究中,畸变屈曲是其结构性能失效的一种重要模式[3]。Lau 等[4]和Hancock[5]发现了受弯构件受压侧翼缘板件会相对于腹板-翼缘连接处先发生转动以及带动腹板发生弯曲的现象,并提出了畸变屈曲概念。之后,Schafer等[6]和Moen[7]相继提出了计算实腹和腹板开孔冷弯型钢构件畸变屈曲强度的直接强度法公式(Direct Strength Method,DSM),一些学者基于此开展了很多研究[8-10],该方法现已较为成熟并被纳入北美规范[11],然而我国《冷弯型钢结构技术规范》(GB 50018-2002)[12]尚缺乏相关规定。目前,有学者[13-14]对单肢构件的畸变屈曲DSM 公式进行了验证和修正,但关于腹板开孔拼合梁的相关研究较少。Roy等[15]对实腹双肢拼合梁进行四点弯曲实验,并通过有限元分析进行了验证和参数分析,研究表明螺钉间距对畸变屈曲承载力影响不大且DSM 公式过于保守。李颖[16]分别对实腹单肢槽钢梁和背靠式组合梁进行了有限元参数分析,通过对比拟合了组合效应系数公式。Wang和Young等[17-18]对单孔拼合梁的畸变屈曲性能进行了试验研究和模拟分析,认为当前畸变屈曲公式较为保守。
为了对腹板开孔冷弯卷边槽钢双肢拼合梁的畸变屈曲进行深入研究,在相关试验数据基础上,利用有限元分析了螺钉间距、孔洞大小和孔洞间距3 种因素对开孔拼合梁畸变屈曲承载力的影响,并评估和修正了相应的直接强度法公式。
1 有限元模拟及验证
文献[18]对腹板开孔冷弯卷边槽钢拼合梁进行了四点弯曲实验,本文试件横截面及加载示意图均参考此文献。通过有限元模拟和实验对比来验证模型的可靠性。由于构件对称,为了减小运算规模,使用ANSYS 有限元软件建立了半跨梁。单元选用shell 181,钢材性能采用理想化双折线等向强化模型。在模拟基本构件间的相互作用时,对腹板区域设定了面-面接触属性,法向接触关系采取增强拉格朗日算法,切向关系设定为无摩擦[19]。为了简化加载位置处的加劲肋,使用多点约束MPC184 刚性梁单元将加载点处的翼缘和腹板有效区域耦合至参考点。同时,该单元也被用于模拟自攻螺钉。有限元网格尺寸为10 mm,但在圆孔处采用了2 mm 加密网格,模型如图1所示。为模拟简支边界条件,约束参考点A 处X、Y方向的平动自由度以及绕Z向的转动自由度,跨中截面节点约束Z向平动自由度和绕X、Y向的转动自由度,在参考点B 处施加竖向集中力。结构在计算到屈曲时,刚度矩阵会产生突变导致不收敛,采用位移荷载控制,用ANSYS 提供的基于耗散能比例的自动稳定方法,保证了模型的收敛性。有限元分析先进行特征值屈曲分析,通过一阶模态施加初始缺陷,之后进行非线性屈曲分析。
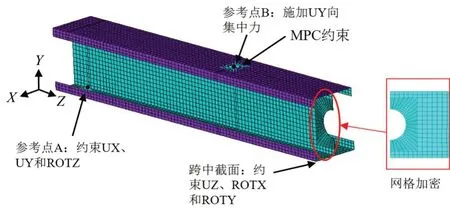
图1 有限元模型
为验证模型的有效性,构件命名规则、截面尺寸、材料参数、最大初始缺陷值均取自文献[18]。试验和有限元的屈曲模式对比如图2所示。

图2 试验变形与有限元变形示意图
图3所示为试验和有限元荷载-曲率曲线,纵坐标的弯矩M=FLs,F为施加的集中力,Ls为边界约束到集中力的水平段距离。本文构件编号与文献[18]中编号一致,以图3中OH0.5T1.9-136为例,O代表开口构件,H 代表跨中腹板开一个孔,0.5 表示孔高比(孔径与腹板高度比值),1.9 和136 分别表示构件厚度和腹板高度(单位为mm)。从图2 和图3 中可以看出,有限元与实验结果的弯矩-曲率曲线基本吻合,表明有限元模型能较好地模拟试验构件的弯曲性能,验证了模型的可靠性。表1 给出了6 组构件有限元与试验承载力结果,二者比值的平均值为1.01,标准差为0.019。
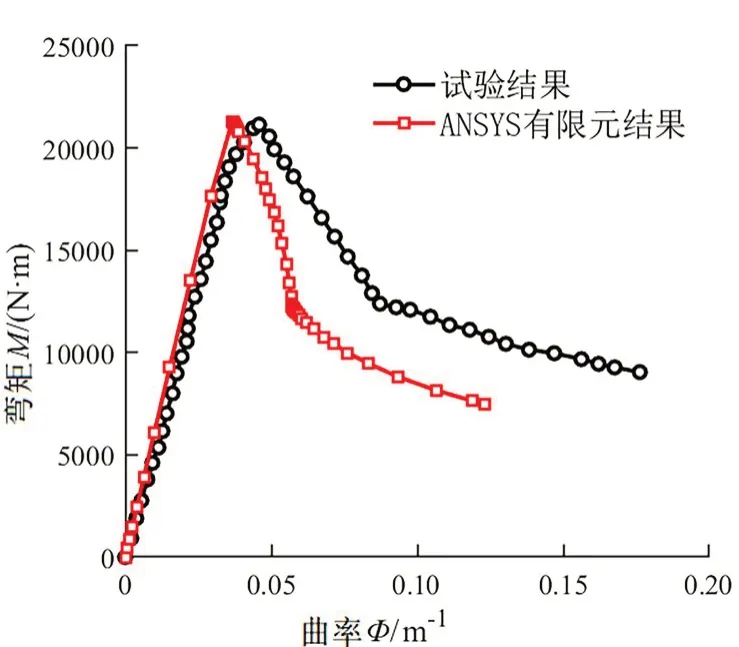
图3 OH0.5T1.9-136构件有限元与试验[18]弯矩-曲率曲线对比
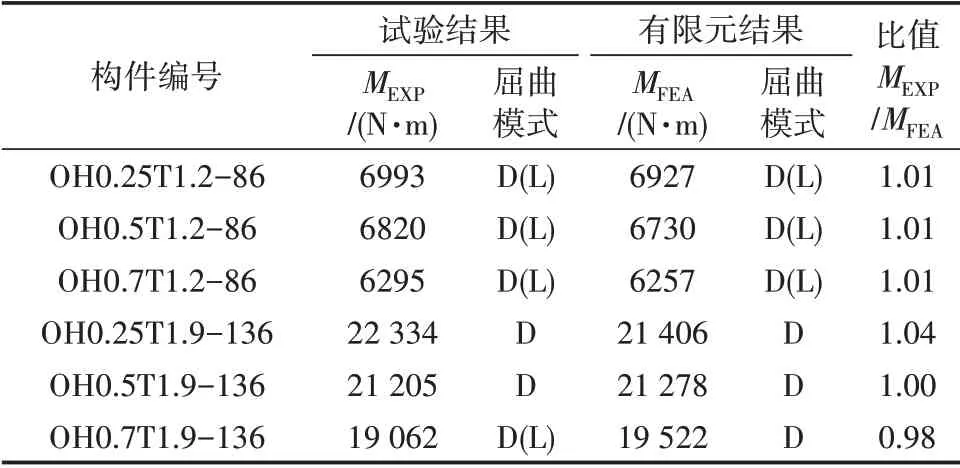
表1有限元与试验[18]受弯承载力对比
2 参数分析
参数分析构件的弹性模量为205 GPa,泊松比为0.3,屈服强度为390 MPa,构件的初始几何缺陷最大值取0.5 倍的截面厚度。 构件命名规则以“H150T1.4S150A300R0.5-L1200”为例,其中,H、T、S、A、R和L分别代表了腹板高、截面厚度(如T1.2表示厚度为1.2 mm)、螺钉间距、孔洞间距、孔高比以及纯弯段长度。参数分析涉及了H150(h=150 mm,b=65 mm,c=15 mm)、H200(h=200 mm,b=75 mm,c=20 mm)和H300(h=300 mm,b=100 mm,c=20 mm)3种截面。
2.1 螺钉间距的影响
通过改变螺钉间距,分别对上述截面构件进行了有限元分析。图4所示为不同螺钉间距下的组合梁弯曲承载力对比。
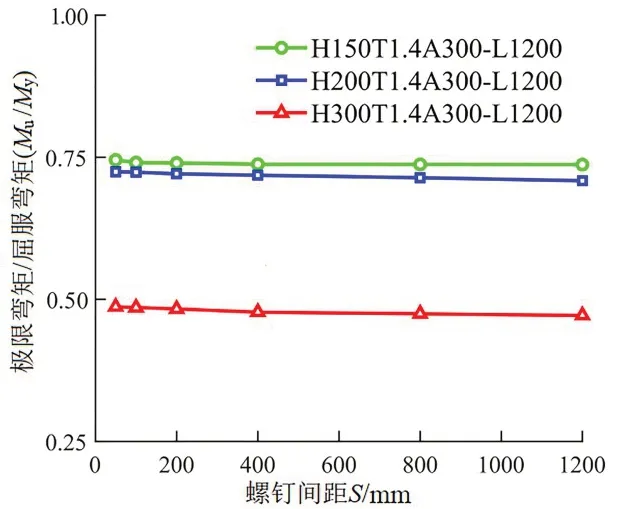
图4 不同螺钉间距下的组合梁弯曲承载力对比
从图4 可以看出,构件的承载力随着螺钉间距的增加而降低。螺钉间距从50 mm 增至1200 mm,H150、H200、H300构件的弯曲承载力降低幅度均较小,表明螺钉间距对构件畸变弯曲承载力影响较小。这是因为腹板处的螺钉对翼缘和卷边几乎没有约束作用,只起到了连接作用。
2.2 孔洞大小的影响
本文选取了0、0.25、0.50、0.65、0.80 共5 种腹板孔高比,对H2000S2000A300-L1200 的3 种不同厚度的构件进行了分析。图5对比了具有不同孔洞尺寸的构件的承载力结果。构件的承载力随厚度的增大而增大,随着孔高比的增大而减小,当孔高比小于0.50 时承载力下降幅度较为平缓,而当孔高比大于0.50 时承载力下降幅度陡然增大。显然,对于发生畸变屈曲破坏的构件,孔洞大小有较大的影响。这是因为腹板开孔减小了腹板刚度,也减弱了腹板对受压侧翼缘和卷边的约束作用。
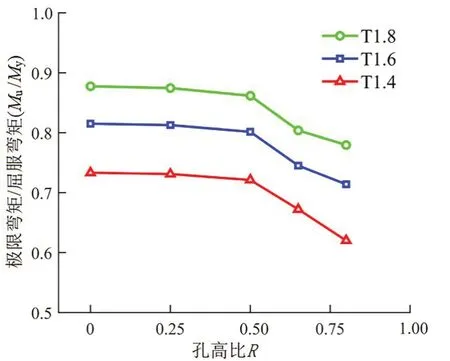
图5不同孔洞大小下的组合梁弯曲承载力对比(H200S200A300-L1200)
2.3 孔洞间距的影响
对不同孔洞间距下的H150S150R0.5-L1800、H200S200R0.5-L1800 和H300S300R0.5-L1800 构件进行分析。图6对比了不同孔洞间距下的组合梁弯曲承载力。以H300 构件为例,图6 中可见,随着孔洞间距的增加,构件的承载力逐渐增大。其中,当孔洞间距从200 mm 增至450 mm 时,构件的承载力逐渐增大但幅度较小,这说明对于受畸变屈曲控制的构件,孔洞间距的影响并不明显,这是由于受孔洞间距变化范围较小的限制,使得屈曲半波长内孔洞面积减小不多,并不会过多影响构件畸变屈曲性能。
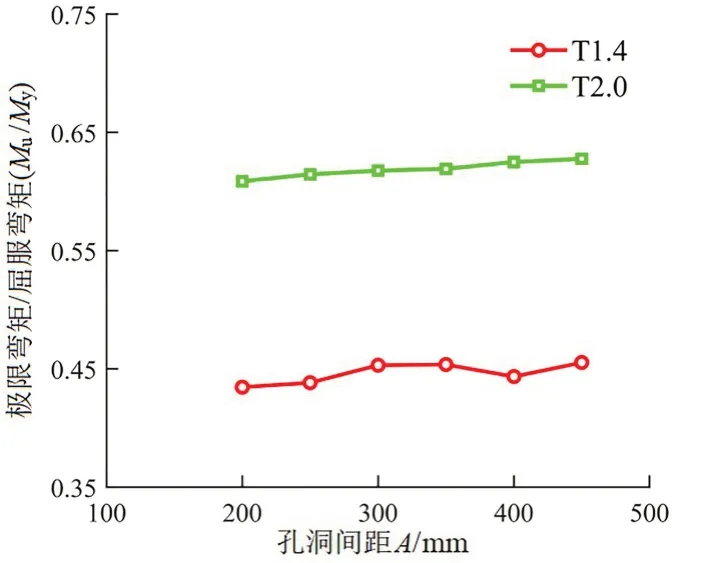
图6不同孔洞间距下的组合梁弯曲承载力对比
3 开孔冷弯卷边槽钢背靠背组合梁直接强度法研究
3.1 冷弯型钢构件DSM公式
北美冷弯型钢设计规范[11]给出了腹板开孔冷弯型钢单肢构件受弯承载力直接强度法计算公式,公式中通过引入净截面边缘屈服弯矩Mynet来度量开孔对构件承载力的影响,其中构件发生畸变屈曲(Mnd)的DSM计算公式如式(1)~(5)所示:

式中:λd、λd1、λd2、Md2均为无量纲参数,My为毛截面边缘屈服弯矩,Mynet为净截面边缘屈服弯矩,Mcrd为弹性畸变屈曲临界弯矩。
拼合梁在发生畸变屈曲时,基本构件间独立发生屈曲,因此本文将2 倍的单肢开孔卷边槽钢受弯构件的DSM 计算结果作为拼合构件的计算值。单肢构件的弹性临界屈曲荷载Mcrd的计算方法主要包括有限条法和理论解析法,有限条法不适用于腹板开孔构件,故本文使用文献[20]的理论算法。
3.2 参数分析结果与DSM 畸变屈曲公式的对比和修正
利用DSM 公式(式(1)~(5))计算了参数分析构件的畸变屈曲承载力,并将DSM 公式结果与有限元结果进行对比,如图7 所示。从图7 可以看出,大部分参数分析数据点基本都位于DSM 公式曲线(图7中虚线)上方且偏离度不大,但是对于大孔洞的构件(η= 0.85,η=Mynet/My)来说,数据点偏离较大,部分结果比值达到1.2,参数分析计算结果与DSM公式计算结果的比值的平均值为1.07,标准差值为0.058,说明原始DSM畸变屈曲公式对于大孔洞的拼合梁较保守。
为了提升DSM 畸变屈曲公式对大孔洞构件的计算准确度,对该公式进行了修正,修正公式如式(6)~(12)所示:

式中:Mcrd,s为单肢开孔构件的弹性畸变屈曲临界荷载,可查阅文献[20]相关公式进行计算,ψd、γd均为修正值。
根据修正公式获得的曲线如图7 中实线所示。由图7 可知,参数分析结果与畸变屈曲修正公式结果更吻合,且两者结果比值的平均值为1.01,标准差为0.057,说明修正后的公式能较好地计算构件畸变屈曲承载力。
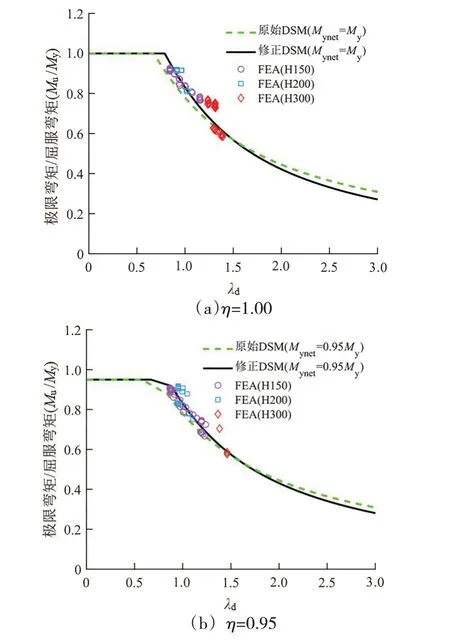

图7 开孔拼合构件DSM修正曲线及有限元散点对比
4 结 论
用有限元方法对腹板开孔冷弯卷边槽钢双肢拼合梁的畸变屈曲性能进行研究,考虑了螺钉间距、孔洞大小、孔洞间距3种因素对构件畸变屈曲承载力的影响,得到以下结论:
(1)构件的承载力随着螺钉间距的增加而降低,且螺钉间距增加较大时,弯曲承载力降低幅度均较小,说明螺钉间距对发生以畸变屈曲为主破坏的构件承载力影响较弱。
(2)受畸变屈曲控制的构件承载力随厚度的增大而增大,随着孔高比的增大而下降,且当孔高比超过0.50 时,孔高比对发生畸变屈曲破坏的构件的影响越大,即孔洞大小的影响较大。
(3)随着孔洞间距的增加,构件的承载力逐渐增大,但增大幅度较小,即孔洞间距对承载力影响不大。
(4)将参数分析结果与DSM 公式结果进行了对比,并对DSM 畸变屈曲公式进行了修正,结果表明,原始的DSM 畸变屈曲公式对于大孔洞拼合梁偏保守,而通过修正后的公式计算构件畸变屈曲承载力更为准确。
