车辆载荷作用下桥梁结构承载力试验分析

惠小磊 张国强 谢 丹

（1、陕西交控市政路桥集团有限公司，陕西 西安 710065 2、西安公路研究院有限公司，陕西 西安 710065 3、陕西西公院工程试验检测有限公司，陕西 西安 710065）

1 桥梁工程概况

为便于理解，本文以我国某桥梁工程为例展开分析，该项目全长约787m。该桥梁的上部结构选用连续箱梁，其材料为预应力混凝土，采用工厂预制、现场装配的方式完成施工。其中，上部结构的布置按照5×30+4×（4×30）+5×30m为标准。下部结构则设计为柱式墩台并借助桩基来提升结构稳定性。通过设计方案可以发现桥梁的景观设计主要集中在第1～4 跨、第11～15、第23～26 跨三部分，且景观设计以“长廊”造型为主，在表面涂刷油漆来进行美化。该项目所采用的的设计荷载标准为公路-Ⅱ级。

2 承载力试验方案设计

综合考虑结构分析结果及现场调研情况，最终将第22跨定为研究分析对象。

2.1 静载试验

2.1.1 内力分析与计算。根据上文可以发现该项目的设计荷载等级为公路-Ⅱ级，且其上作用的人群荷载选定为3.0KN/m2。基于本项目设计方案所用的桥梁结构型式，借助有限元分析软件完成计算[1]，根据所绘制的包络图可以发现在上部设计荷载下结构内出现的最不利截面为第22 跨的0.4L断面以及第23 跨的中断面。同时，在桥梁结构之上施加公路-Ⅱ级荷载进行分析得到各个截面的弯矩分布情况。遵照我国现行规范即可计算得到截面弯矩控制值如表1 所示。

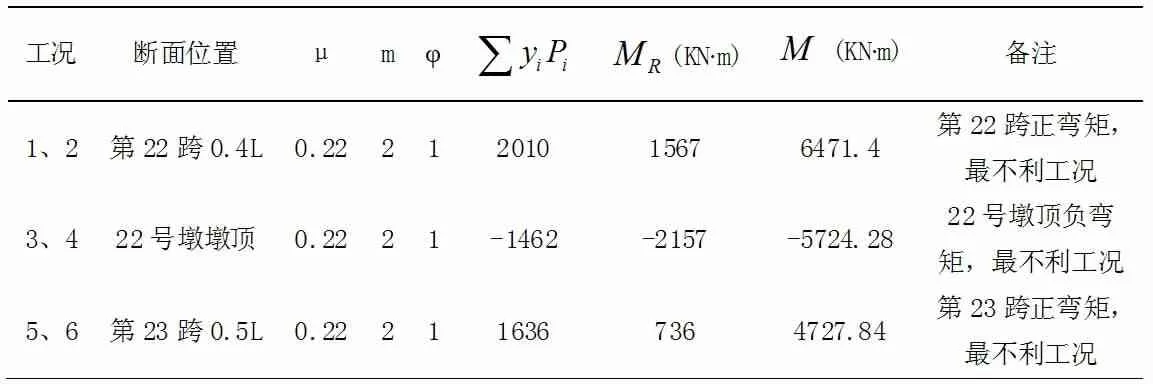
表1 测试断面设计荷载控制弯矩计算表

表格中弯矩值M由下式计算而得：

式中：μ 为冲击系数；m 为车道数；φ 为车道横向折减系数；∑yiPi指代影响线坐标与单列荷载效应的乘积。

2.1.2 加载效率。按照本研究设定的设计荷载（公路-Ⅱ级）以及试验荷载（4 辆重车加载）下主梁结构中弯矩影响线的分布可以分别得出不同工况下其所相应的弯矩值，两者之间的比值也即加载效率[2]。根据现行试验规范要求，静载试验应控制加载效率在合适的范围内方可认定试验为有效，其中效率系数ηq应当在0.95-1.05 的范围内，其中ηq=Ss／(S×(1+μ))。

Ss- 在静力试验荷载下，某组试件中控制截面最大变形或最大内力所对应的计算效应值；

S- 在设计荷载作用下，某组试件中控制截面最大变形或最大内力所对应的最不利效应计算值（不计冲击系数）。

在本研究中，通过试验得出表2 所示的加载效率，其各项参数均满足现行规范要求，也即试验加载有效。

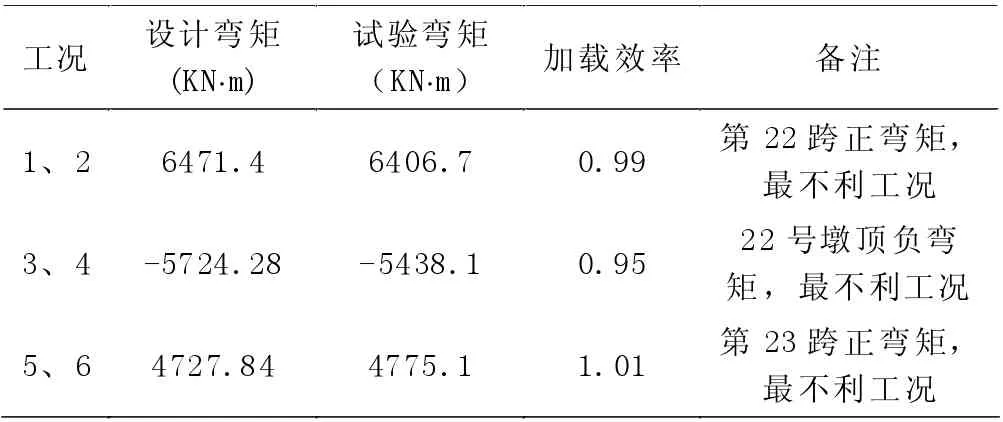
表2 加载效率表

2.2 动载试验

测定在车辆通过时桥梁结构中预设测点所反馈的加速度信号，同时借助加速度振动时程信号做出初步处理，得到相应的频率分析[3]。

在结构分析中，一般可采用对数衰减率δ、阻尼比Dr表征结构的阻尼水平。为便于操作，在实际研究中可取衰减曲线中若干波计算其平均值作为衰减率。

2.3 测点布置

2.3.1 静载试验测点布置。为得到试验荷载下桥梁结构实际所发生的变形情况，在本研究中分别于第22 跨的0.4L处和第23 跨的0.5L、第18 跨的0.4L位置布置测点，分别测定其挠度、应变情况。此外，还在22 号墩支点截面的底部及腹板处各安设了20 个测点用于得到其应变情况。由于墩柱顶部负弯矩的最不利工况条件下所对应的边跨、次边跨主梁挠曲均小于最不利工况条件下的挠曲，因此对负弯矩工况并未布置相应的测点。

根据事先确定的贴片方案，先用粉笔在贴片位置定位，然后用角磨机打磨、擦拭干净后逐个贴片；安装机电百分表时，用磁力表座将机电百分表固定在支架上，调整百分表的位置，使其测头在适当位置，最后用测试线将应变片和机电百分表与仪器逐一连接，并作详细记录。安装工作就绪后，还需要对应变片、百分表以及导线等做出全面的核查，排除潜在的风险，同时调试检查仪器设备。

2.3.2 动载试验测点布置。动载试验需要分别在各跨的0.4L和0.6L位置处各设置一个测点，测定结构所发生的加速度响应。根据我国现行规范要求，采用单辆车辆按照40Km/h 的速度标准通过桥面并刹车产生激振，由此传感器即可得到相应的振动曲线，并同时借助分析软件得到结构的自振周期等基本参数。

2.4 试验加载

准备好加载车辆，按加载先后顺序停放于试验桥梁以外待命，在加载前，将加载车辆分散的放在桥梁上进行预压，以减少试验过程中桥梁的非弹性变形的影响。按确定的试验工况，在桥面上用粉笔标出车辆停放位置，在加载时，应当确保试验所用车辆停放在指定的位置。对于现场开展的试验应同时设置两个平行的试验组，若两组所得到的实验数据具有较好的拟合性，则可认为试验数据可靠，即可结束该次试验；若两组试验数据的拟合性较差，则应当探究其成因并重新开展试验测试。此外，在本研究中，应当将试验实测数据与理论分析数据进行横向比对。试验加载应当按照多级加载、逐级进行的原则，将全部荷载划分为三个不同的等级，在每一级的荷载水平下可指挥车辆驶入预定位置并测得其所相应的变形情况，将其与理论分析值比对。若研判认为结构仍处于弹性状态，则可再次施加下一级荷载。按照上述原则逐级加载至最大荷载后还需逐级完成卸载[4]。在静载实验中，为降低混凝土材料受力发生残余应变的不利影响，当加载至预定水平后则需要及时关闭发动机，并保持这一状态至少10min，直至桥梁结构的变形趋于稳定后方可读取传感器的参数。而在每次卸载过程中，当车辆行驶出实验区段后至下一次加载之前应至少保持10min 的间隔。

3 承载力试验结果分析

通过MIDAS建立与本研究相应的有限元分析模型，同时测定结构在不同工况条件下的变形、位移，核验其动力特性。全桥共划分为504 个节点，480 个单元。

3.1 静载试验结果分析

3.1.1 荷载横向分布。该桥各梁的理论荷载横向分布系数按刚接梁（板）法计算，根据各梁的横向分布影响线及两种工况下的车辆荷载在影响线上的具体位置，并以此计算得到梁体的横向分布系数[5]。试验研究中为计算得到横向分布系数，一般可首先测定不同截面的挠度情况，同时采取式（2）完成计算。

式中：mi为试验荷载下，某一量测截面第i 片主梁的荷载横向分布系数；fi为试验荷载下，某一量测截面i 片主梁的测点挠度；n 为主梁片数。

该桥第22 跨主梁实测横向分布和理论值对比如图1、图2 所示。

根据图1、图2 中的曲线分布可以得出结构在有限元分析中得到的横向分布与试验实测拟合性较好，也即结构的横向连接性良好。

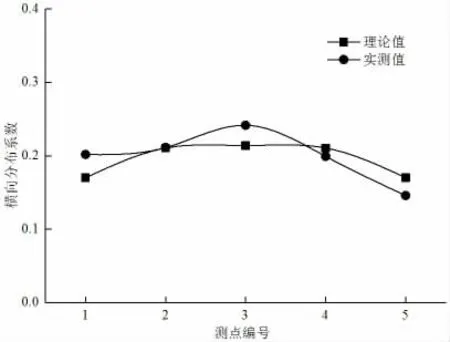
图1 第22 跨主梁横向分布系数对比（0.4L 处中载）

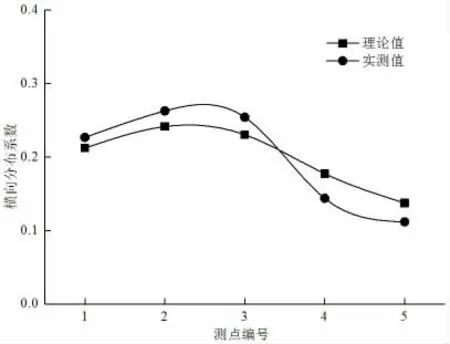
图2 第22 跨主梁横向分布系数对比（0.4L 处偏载）

3.1.2 挠度。在本研究的挠度测试中，共计加载16 次，且对于每个不同工况均按2 次进行加载，将两次加载下所测得的挠度取平均值认定为实测值。对不同荷载水平下梁体挠度的试验实测值与理论分析值进行比对发现，实测值总体表现出低于理论值的分布，且远低于L/600=50mm的规范要求值，挠度校验系数为0.59。表明桥梁结构整体受力状况良好。挠度比较情况如图3、图4 所示。

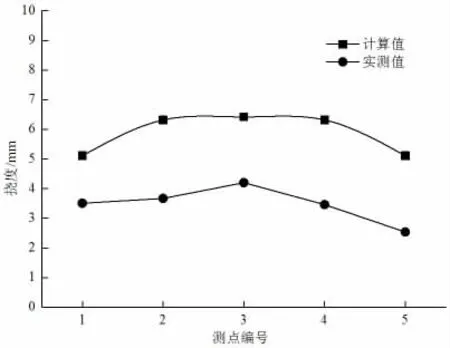
图3 第22 跨主梁实测挠度与计算值对比（0.4L处中载）

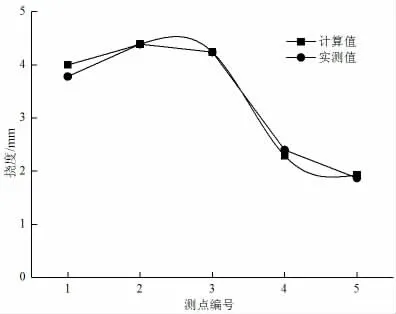
图4 第22 跨主梁实测挠度与计算值对比（0.4L处偏载）

3.1.3 应变。在本研究的应变测试中，共计加载24 次，且对于每个不同工况均按2 次进行加载，将两次加载下所测得的挠度取平均值认定为实测值。对不同荷载水平下梁体挠度的试验实测值与理论分析值进行比对发现（如图5、6），实测值总体表现出低于理论值的分布，且在中载及偏载下0.4L位置的挠度校验系数分别为0.62、0.69，表明桥梁结构整体受力状况良好且仍处于弹性状态下，具有足够的裕度储备。

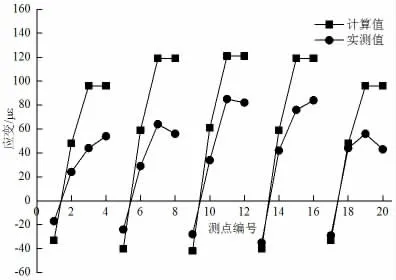
图5 第22 跨主梁实测应变与计算值对比（0.4L处中载）

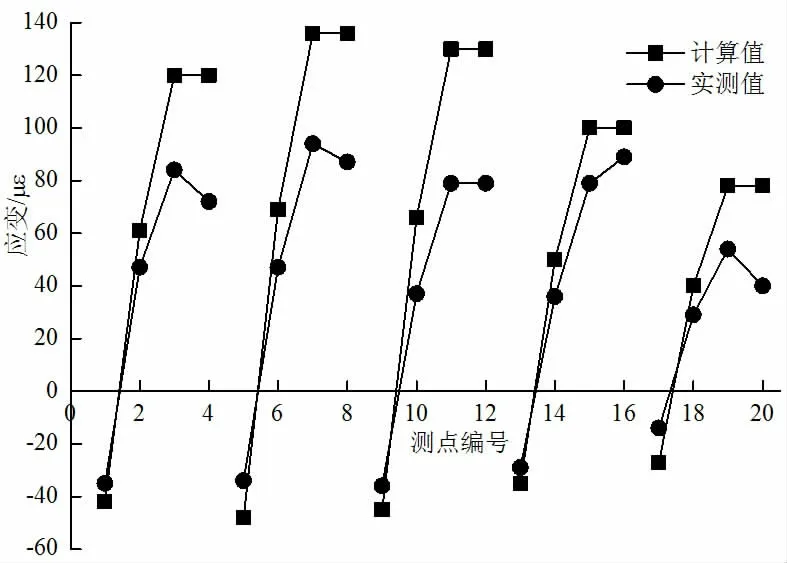
图6 第22 跨主梁实测应变与计算值对比（0.4L处偏载）

3.2 动载试验结果及分析

动载条件下的有限元分析主要借助MIDAS软件完成，由此得到一阶频域振型如图7 所示。

图7 理论一阶频率振型图

在本研究的动载试验中，分别按照两种不同的加载方式对结构进行作用，其中第一种采取车辆刹车的方式，第二种则让车辆直接穿越桥梁，这两种不同的作用方式所产生的激振均具有频带宽和激励强的特点[6]。试验将传感器所得到的数据作为标准，下面将第22 跨所发生动力响应的时域、自功率谱信号以及阻尼比作为研究对象。得到结构的频率试验实测值与理论分析之比如表3 所示。

表3 频率与阻尼比一览表

根据试验实测得到的结构基本动力特性参数可以发现：a.绘制得到的振动曲线与振动规律之间存在较好的拟合性，且在动力作用下主要为一阶振动，其中竖向振动基频的试验实测值较理论分析值更大，上部结构的动力特性比较好且刚度较大。b.一般而言，结构的阻尼比参数大多局限在0.01～0.08 的范围内，试验实测得到的阻尼比为0.0152，这表明结构耗散能量的能力较好。

4 结论

在本研究中，试验加载效率介于0.95 与1.01 之间，与规范相应的加载要求相符，认定为有效。

4.1 通过静载试验可以发现：在不同工况下主梁结构各个测点得到的挠度均低于理论分析值，且挠度的校验系数介于0.44 与0.91 之间，其相对的残余变位小于20%；此外，其他测点位置得到的应变也均低于理论分析值，其校验系数介于0.44 与0.96 之间，相对残余变位小于20%；根据上述试验结果可以发现，该桥梁具有良好静力学性能，其各项强度均满足要求。

4.2 通过动载试验可以发现：试验实测得到的时域曲线与理论规律之间的拟合性较好，其中阻尼比、振动时域等基本参数均满足要求。其中，试验实测得到的一阶频率较理论值更大，阻尼比介于0.01 与0.08 之间，这也表明结构刚度指标符合要求。

4.3 在试验全过程中结构的控制截面位置均未发生明显的开裂。总体来看，可认为该桥梁能够达到公路-Ⅱ级荷载的设计标准。