不同类型温度导热模型的开发与运用

王墨南，吕立华

（宝山钢铁股份有限公司中央研究院 智能制造所，上海 201999）

加热/冷却过程是钢铁生产工艺的重要环节，连铸、加热炉、热处理过程都涉及到钢铁生产温度的改变，加热/冷却质量直接影响钢铁产品的最终质量。钢铁生产中物料对象的温度计算依靠温度跟踪在线模型反应，温度模型的准确性一直是重要研究课题。随着生产的发展，产品越来越多、质量要求越来越高，对温度模型的准确度要求也越来越高。近年来计算机应用技术和模型优化算法等得到迅速发展，可以应用这些先进科学技术为生产服务。

本文针对不同种类、形状的钢铁产品，基于不同类型的导热模型，设计温度在线跟踪模型，查看钢铁产品在生产中的温度状态，满足了生产单位的各种功能要求，得到了较高的精度。

1 温度跟踪模型基本情况介绍

1.1 功能概述

温度跟踪模型具有下列功能：

根据控制系统给出的尺寸信息、位置信息、时间信息、钢种信息等，结合现场热电偶温度信息，运用温度计算模型模块计算出对象物料各个区域的实时温度。

1.2 模型系统框架

温度计算模型模块通过数据库得到对象物料在线跟踪数据（位置信息、几何信息、类型、激励电文、时间信息等）和热电偶实时温度数据，再把物料实时温度计算结果更新至数据库中，更新后的数据在软件画面上展示出来（见图1）。

图1 温度跟踪模型系统框架图

2 温度计算模型介绍

温度计算模型一般由导热计算模块和边界计算模块两部分组成。

受热物料除了外部边界受到传热以外，内部的温度分布通过导热传热进行。导热的计算可以根据傅里叶方程确定，不同形状的物料导热方程的建立略有不同。

2.1 矩形导热模型

钢铁生产过程中最常见的是矩形物料，如板坯、厚板等。可以在笛卡尔直角坐标系下建立离散网格划分，同时为了简化模型，工程上常用的导热模型仅考虑物料内部厚度和宽度方向的二维热传导（见图2），网格数量i×j。

图2 笛卡尔坐标系下离散化网格划分示意图

根据热平衡方程，物料内节点（m，n）虚线区域的二维热传导方程可以描述为式（1）：

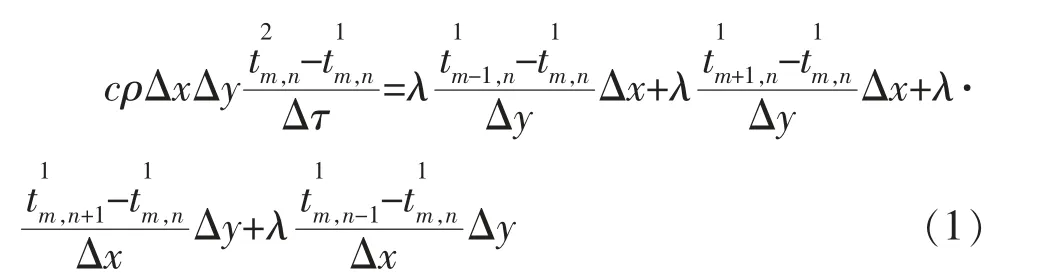
式中：ρ—物料密度，kg/m3

c—物料比热，J/（kg·℃）

λ—物料导热系数，W/（m·℃）

Δx—宽度方向物料一小段网格的距离，m

Δy—厚度方向物料一小段网格的距离，m

Δτ—时间步长，s

t—板坯温度，K，t1为当前时刻温度，t2为下一时刻温度

m、n—板坯内某个结点的坐标位置

若采用半显式半隐式的交替算法（ADI算法），不但能够快速准确计算，同时又能提高方程稳定性，收敛判定条件也会略宽松。

分别在宽度和厚度方向各交替做一次显式和隐式计算，第（m，n）点的方程为式（2）、式（3）：

式（2）、式（3）无法像显式方法那样直接迭代求解，必须联立i×j个节点上各个类似式（2）、式（3）的热平衡方程组求解，即基于追赶法（TDMA方法）计算，得到下一时刻的板坯温度分布。

2.2 圆形导热模型

钢铁生产过程中圆柱形、圆形、扇形物料也非常常见，如圆棒、钢管等。需要在极坐标系下建立离散网格划分，同时为了简化模型，导热模型仅考虑物料内部弧度和角度方向的二维热传导，并且考虑圆的对称性，一般只需要考虑1/2圆即可（见图3），网格数为i×j。

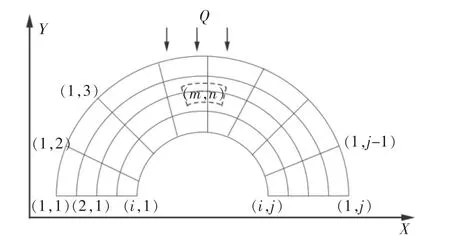
图3 圆柱坐标系下离散化网格划分示意图

根据热平衡方程，物料内节点（m，n）虚线区域的二维显示热传导方程可以描述为式（4）：

式中：Δr—径向物料一小段网格的距离，m

Δφ—弧度方向物料一小段网格的角度，m

rm—点（m，n）到圆心的距离，m

采用半显式半隐式的交替算法（ADI算法），分别在径向和角度方向各交替做一次显式和隐式计算，第（m，n）点的方程为式（5）、式（6）：

2.3 组合型导热模型

除了以上两种形状的物件外，钢铁生产过程中也有可能出现形状较为特殊的物件，既包含矩形也包含圆形，如钢锭、连铸外壳、卷铁心等，如图4所示，无法用一个单一的坐标系建立离散网格划分。这时，可以考虑通过直角坐标系和极坐标系拼接的方式建立离散网格划分。同时为了简化模型，导热模型仅考虑物料内部矩形处厚度和宽度、圆形处弧度和角度方向的二维热传导，并且考虑对称性，一般只需要考虑1/4即可，如图5所示，由两个直角坐标系和一个极坐标系组成，网格数为i×p。

图4 钢锭3D示意图

图5 直角和圆柱坐标系拼接下的离散化网格划分示意图

在两种网格的非交界处，对矩形和扇形分别划分网格，注意矩形厚度方向和扇形径向划分网格数要一致且对应。非交界处依然按照原有坐标方式在各个节点处建立导热微分方程。这里不再重复介绍。

在两种网格的交接处需要特殊处理，直角坐标系下的单元节点与极坐标系下的单元节点需要合并处理，交界处的单元体积需要两个坐标系下的相关体积合并，热流也需要合并计算。

两种坐标系交界处节内点（m，n）为图5虚线区域、图6实线区域，其中一半区域为矩形一半区域为扇形，该区域上的二维热传导方程可以描述为式（7）：

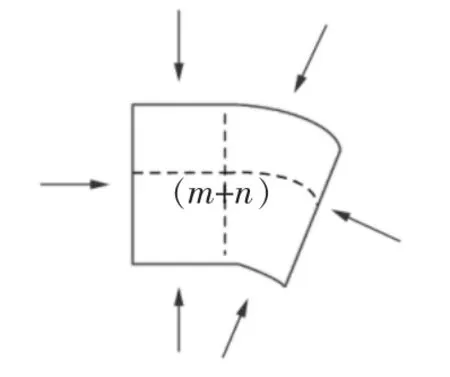
图6 直角和圆柱坐标系交界处的节点热单元示意图

该方法同样也可采用收敛条件更加宽松的半显式半隐式的交替算法。

2.4 边界条件

在加热或冷却过程中，物件在温度变化时主要通过对流与辐射完成与外界的换热。

对流方程如式（8）：

式中：Q（i）—物件表面节点i处的热流量，W

Ai—物件表面节点i处的受热面积，m2

h—对流系数，通过实验或经验公式获得，W/（K·m2）

T（i）—物件表面节点i处的温度，K

Te—外界环境温度，K

此外，物件在加热炉或热处理炉等高温工艺的传热方式主要是通过热辐射来获取热量，当高温环境足够广大时，简易的辐射方程如式（9）：

式中：ε—发射率

σ—斯忒潘-玻耳兹曼常数，5.67×10-8W/（m2·K4）

该方法简单有效，在实际运用中广为使用。

辐射热流也可根据各个辐射对象之间建立辐射网络方程精确计算。具体热平衡关系由式（10）～式（12）体现。

式中：下标i，k—分别表示系统内不同辐射体i和辐射体k

φ—辐射体的辐射角系数

S—辐射体的有效辐射表面积

J—辐射体的有效辐射量

R、ε—分别为辐射体的反射率和发射率

H—外界向辐射体投入的辐射总量

E—辐射体的黑体辐射量，E=σT4，其中，T为辐射体表面绝对温度，通过测温装置测量

n—辐射体个数

联立方程计算出的有效辐射J，也就是辐射热量Q。

2.5 相变问题

在有些钢铁生产过程中，如连铸，在冷却过程中会出现凝固的相变过程，同时释放潜热。可以根据固液相线，采用等效比热法，在相变过程中通过计算对象在不同温度下改变比热的数值从而间接表示释放潜热。该模型已被证实方便、简单、有效，适用范围广。

3 结论与应用案例

各类导热模型在钢铁工艺计算中运用广泛，包括连铸、热轧、钢管的生产等，尤其是相关温度跟踪模型被大规模在线运用，测试表明长期运行稳定。

根据物件对象形状的不同选择合适的导热模型可以提高温度计算的精度。边界条件除了需要理论计算外还需结合实验与实践经验，计算出的对象温度才可以更好地反应实际生产情况。

图7为0.5 m×0.25 m的矩形和半径为0.25 m的半圆从室温20℃，上表面受到1 h时长的、1 000℃温度加热后的对流传热（对流系数、物性参数相同）的升温曲线，包括表面升温曲线和平均温度升温曲线。可以看出，在类似条件下，矩形和半圆形的升温曲线相差较大，尤其是平均温度在加热1 h后相差185℃，表面温度相差略小，为67℃。

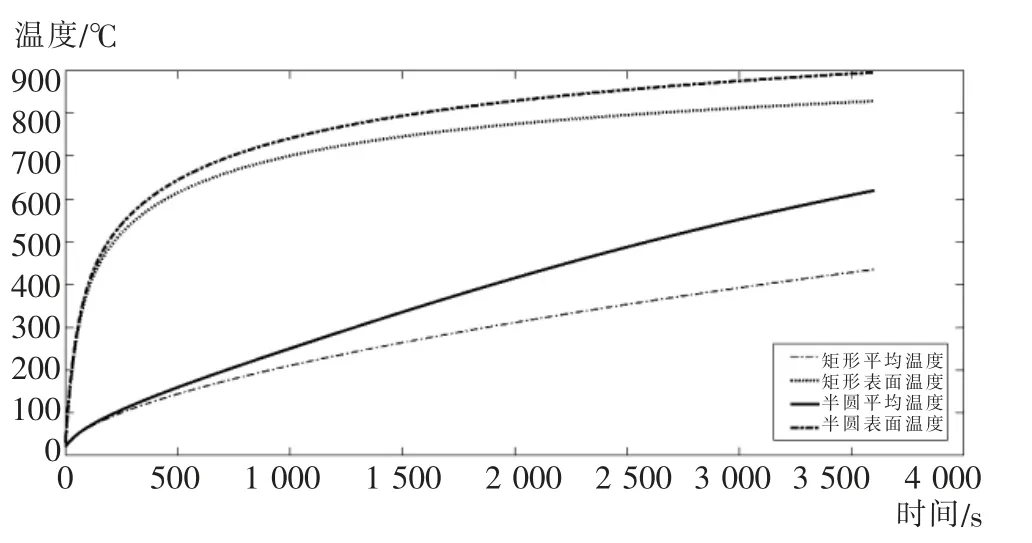
图7 矩形和半圆形升温曲线图

图8为热轧加热炉在线跟踪画面，可实时输出炉内各板坯温度，方便工艺人员控制加热炉温度。

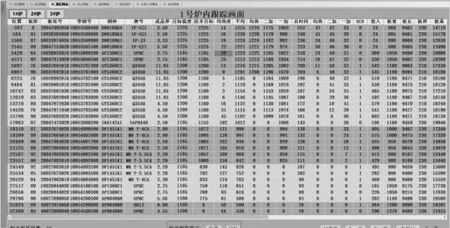
图8 加热炉在线跟踪画面