解三角形的五种意识与备考建议

广东 刘光明

解三角形知识是全国卷历年高考的必考知识，试题难度中等，要求思维灵活.一方面，《普通高中数学课程标准(2017年版2020年修订)》明确要求“借助向量的运算，探索三角形边长与角度的关系，掌握余弦定理、正弦定理.能用余弦定理、正弦定理解决简单的实际问题.”在教学建议中，提出“引导学生运用向量解决一些几何问题”.另一方面，2019年版人教A版新教材中余弦定理、正弦定理的内容安排与原教材相比变化较大：一个变化是这个内容不独立成章，而是平面向量的一部分；另一个变化是余弦定理、正弦定理都用向量方法证明.

基于新课标的要求和新教材的导向，结合高三复习教学实践，处理解三角形问题一般可以从定理、几何、解析、基底和转化五个方面进行探索，下面结合以下例题进行阐述，以期抛砖引玉.

(1)求c；

(2)设D为BC边上一点, 且AD⊥AC, 求△ABD的面积.

一、定理意识

所谓定理意识就是指借助正弦定理、余弦定理、勾股定理、射影定理以及三角形内角和定理等与三角形相关的定理实现“边化角”或者“角化边”进行解三角形的自然思维.余弦定理、正弦定理是解三角形的依据，通过由已知元素定量计算其他元素把握三角形这个基本图形，故而定理意识是解三角形的常规认知.

方法1：余弦定理

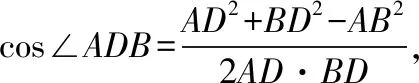
方法2：正弦定理

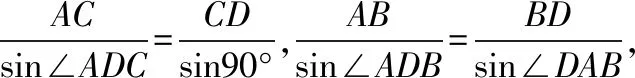
点评：同样关注到了两角互补这一几何特征，但方法2正弦定理的运算显然要比方法1简洁，因此在定理使用过程中也需要不断尝试，合理取舍.

二、几何意识

几何意识是指根据三角形的几何特征，通过合理构造直角三角形、外接圆、平行四边形等特殊的几何图形，利用几何关系进行解三角形的理性认知.三角形本身就是一个几何图形，联想到几何意识解三角形也是直观想象核心素养的自然呈现.

方法3：构造直角三角形

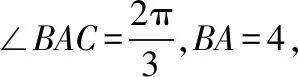
点评：作垂线，一般三角形就能够回归到最熟悉的直角三角形，加之题干中AD⊥AC，构造垂线之后不仅有垂线，还有平行线，更增加了线段间的比例.充分借助已知的角和边，再加一个直角，解三角形便顺其自然.

方法4：构造平行四边形

点评：通过作平行线构造平行四边形，根据平行四边形的性质求解边角关系也是一种巧妙方式，并且从中可以窥探三角形试题的命题思路——从平行四边形中截取一个三角形.

方法5：重心性质

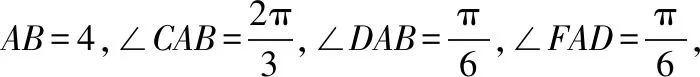
点评：联想到重心性质其实是受到前面求解中点D的启发，才会去思考能不能直接证明重心，从而推导出中线，判断出点D是中点.如果没有前面的思考，此想法不会那么容易独立发现.

方法6：构造外接圆

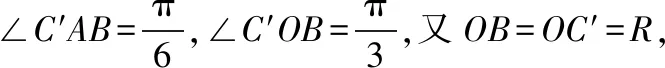
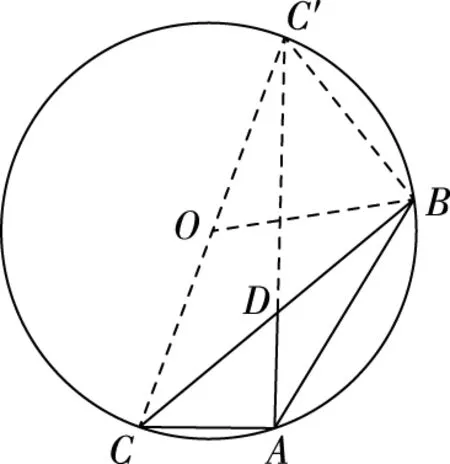
从上述方法3至方法6的推理中不难发现，充分挖掘三角形中的垂直、平行、相似等几何条件，通过作垂线、作圆等辅助方式能够得到边角的等量关系，通过解方程求解出相应的量.但几何关系的寻找要求初中平面几何知识非常扎实，同时直观想象核心素养要求也较高.

三、解析意识

解析意识就是建立坐标系，点坐标化后将几何问题转化为代数运算处理的数形结合思维.三角形是平面几何图形，建立平面直角坐标系后，三角形的顶点都能够用坐标表示出来，再结合解析几何相关的轨迹方程、直线方程、直线与曲线位置关系等知识可进行代数化运算得到结果.

方法7：建系坐标解析法

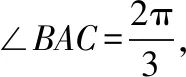
点评：充分利用几何图形中的垂直关系建立平面直角坐标系，使得尽可能多的点落在坐标轴上，这是建系的原则.建系后，点坐标化，未知点则需要假设，然后将条件和结论都翻译成坐标形式，根据解析几何知识进行处理即可.

四、向量基底意识

向量具有明确的几何背景，向量的运算具有明显的几何意义，涉及长度、夹角的几何问题可以通过向量及其运算得到解决.因此引导学生应用向量解决几何问题，让学生掌握平面几何的向量方法.向量基底意识就是选择一组基底，把所要求解的量转化为基底表示，将几何问题转化为向量问题，借助向量的运算解决几何问题的意识.这种方法关键在选择合理的基底，难点在几何与向量间的转化，完美实现了数与形的结合.

方法8：向量基底法

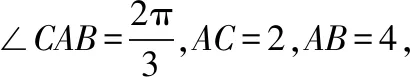
五、转化意识

解三角形中的转化意识就是将所要直接求解的结论，通过借助其他相关的图形间接求解结论的一种思维意识，也是解决数学问题比较常见的思考方向.

方法9：借助面积比

点评：本题中最关键也是最难求解的量就是AD的长度，通过与公共边AD相关的两个三角形的面积比巧妙化解求未知量的困境.

相关试题链接：

【题1】(2021·新高考Ⅰ卷·19)记△ABC的内角A，B，C的对边分别为a，b，c．已知b2=ac，点D在边AC上，BDsin∠ABC=asinC．

(1)证明：BD=b； (2)若AD=2DC，求cos∠ABC．

【题2】(2022·山东德州高三12月联考·18)记△ABC的内角A，B，C的对边分别为a，b，c．已知c2=ab，点D是边AB的中点，CDsin∠ACB=asinB．

(1)证明：CD=c；

(2)求cos∠ACB.

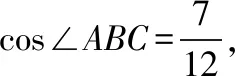
六、备考建议

1.关注定理的生成过程，重视知识的本质

高三解三角形复习课虽是温习所学过的知识，但更是对解三角形的重新认识，对解三角形本质的再升华.因此解三角形复习课需要数学问题驱动定理生成过程的回顾，需要单元主题的视角构建知识网络，进一步促进解三角形本质的认识.如，以问题“叙述并证明正弦定理和余弦定理”“为什么大边对大角？”“为什么两边之和大于第三边”等回顾正弦定理和余弦定理的内容和证明定理的思想方法，并运用定理证明一些常用结论，构建知识体系的同时也感悟解三角形的基本思考方向.

2.树立经典三角模型意识，加强知识间联系与整合

三角形这个几何图形不是孤立存在的，平面向量、解析几何、立体几何甚至数列主题知识的考查都会不经意间用到解三角形的知识.因此在三角形复习中，要提炼一些经典模型，如文中例题和2021年新高考Ⅰ卷解三角形试题，都是用到互补角这一“爪子模型”，另外还有“隐圆模型”“角平分线”模型等.通过识别常见三角形命题情境，快速寻找破题思路.适当引入相关知识的交汇情境，让学生更能够意识到三角形的地位，也体会到“四层”“四翼”的高考要求.

3.夯实几何直观素养，加强运算能力培养

三角形是一个简单却又充满魅力的几何图形，从几何关系的角度能够解决的问题通常都不会进行代数运算.作垂线构造直角三角形、将不规整图形进行割补整合成规整图形、利用三角形外接圆等常见几何方式能够孕育学生的直观想象核心素养，也为解三角形简化运算程序，由形得到数的结论.但也常常遇到方程组的求解，不能绕开计算，故而复习过程中强调方法的同时也要注重计算能力的训练.

4.重视思维的灵活度，提升深度复习质量

解三角形复习课不能仅仅停留在正弦定理和余弦定理这一狭窄的思维空间里，与其他知识复习一样，需要探索一题多解，拓宽思维的广度，增强知识间的关联度，达到知识本质学习的深度.向量和三角形的融合，实现了数与形的完美结合，更能体现向量的工具性，也为解三角形插上翱翔的翅膀.通过“解三角形基本意识”“三角形中的范围问题”“三角形面积问题”等微专题突破解三角形主题知识的复习，以微视角专注提升深度复习的质量.

5.明晰学生易犯错误，规范解三角形的过程表达

大部分学生还是有信心去解答解三角形试题的，主干知识和常规解法都不会存在太大问题，但细节的处理上面还是经常会出现一些小问题，如“忽略角的范围”“角的单位不统一”“定理内容不完整”“方程组求不出来解”等.复习解三角形主题知识时，不要有侥幸或者不屑的思想，踏踏实实严抓学生的规范表述能够为高考增添更多光彩，为数学思维严谨性训练提供沃土.