不完美SIC 下NOMA 系统用户配对和功率分配联合优化*
2022-05-10陈程,李烨
陈 程,李 烨
(上海理工大学 光电信息与计算机工程学院,上海 200093)
0 引言
非正交多址[1](Non-Orthogonal Multiple Access,NOMA)技术是在正交频分多址接入(Orthogonal Frequency Division Multiple Access,OFDMA) 技术的基础上引入功率域的概念,以增加接收端复杂度的代价来提升系统的吞吐量性能[2]。NOMA系统主要依靠在发送端对用户信号进行叠加编码(Superposition Coding,SC)和在接收端使用串行干扰消除(Successive Interference Cancellation,SIC)技术恢复原始用户信号[3]。由于NOMA 系统最大化系统和速率问题是一个非线性混合整数规划问题[4],需要同时考虑用户配对和功率分配对系统和速率的影响,但这种求解方式复杂度较高。因此,大多数研究只是从用户配对或功率分配其中一个角度对系统和速率进行优化。
在用户配对方面,一般是将具有较大信道增益差的用户进行配对[5]。Islam 等人[6]提出最大-最小信道增益用户配对,这样的配对方式存在近零问题,导致系统和速率降低。Mounchili 等人[7]提出了分布式NOMA(Distributed NOMA,D-NOMA)配对算法,保证配对用户间存在最小信道增益差。Mounchili 等人[8]还提出了一种最小距离(Minimum Distance NOMA,MD-NOMA)配对算法,推导出参与配对用户的增益差闭式表达式。相比于规则量化的配对算法,基于启发式的配对搜索算法如爬山算法[9]、模拟退火算法[9]、匈牙利算法[10]、粒子群算法[11]、神经网络[12]等也被应用于用户配对问题中。
在功率分配方面,Fu 等人[13]提出了改进注水功率分配算法;Tong 等人[14]提出了复数域的功率分配方法;Mounchili 等人[8]推导出满足用户服务质量(Quantity of Service,QoS)的功率分配系数闭式解;Gupta 等人[15]从能量效率角度提出了基于Dinklebach 的迭代功率分配算法;Lee 等人[16]提出了基于强化学习的功率分配算法;Huang 等人[17]从和速率、能量效率角度,以及Fathimath Shamna 等人[18]从用户公平性的角度,结合深度学习对功率分配问题进行研究。
然而,上述研究都是单独考虑用户配对或功率分配问题,实际上用户配对方案和功率分配方案互为条件,对系统和速率均有着重要的影响。同时,这些研究都是基于接收端能完美执行SIC 的假设,但由于接收端硬件处理能力不足、信号重构异步等因素[19],接收端会存在干扰残留,导致系统和速率降低。本文基于接收端不完美执行SIC 的假设,提出一种用户配对和功率分配联合优化(Joint optimization of User Pairing and Power Allocation,JUPPA)算法。
1 系统模型
考虑单基站蜂窝下行NOMA 系统的L个用户均匀分布在半径为R的小区中,形成M个用户对,每个用户对中有N个用户(M≤L/N),相同用户对内的用户在同一资源块上复用。系统总带宽为B,用户对带宽为Bw。
假设基站侧已知用户信道状态信息(Channel State Information,CSI),且信道增益满足其中,hi,l为基站到用户对l中用户i的信道矩阵;ωl为预编码矩阵。定义用户对中信道增益较大者为强用户,信道增益较小者为弱用户。
如图1 所示,按照NOMA 系统工作原理,基站采用叠加编码技术发射信号并进行功率控制,信道增益越大的用户,基站分配的功率越低。在接收端,用户根据串行干扰消除原则恢复信号,将信道增益较大的用户视为干扰,依次滤波解码信道增益较小的用户并进行信号重构,移除该重构信号后,顺序解调恢复其他用户信号。

图1 单基站蜂窝下行NOMA 系统
在传统NOMA 系统中,经过发射端的信号叠加和接收端的串行干扰消除,接收端用户信干噪比(Signal to Interference plus Noise Ratio,SINR)为:
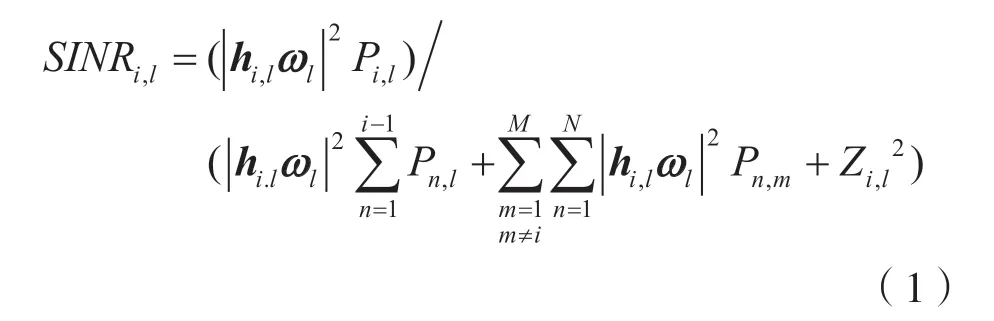
式中:Pi,l为用户对l中用户i的功率;分子为目标用户信号功率;分母中第1 项为用户对l中其他用户的干扰信号功率,第2 项为不同用户对对间干扰;Zi,l~CN(0,1)为高斯白噪声。
受接收端硬件处理能力不足和信号重构异步等因素影响,实际接收端并不能完美执行SIC,因此用户的接收信号中还存在已解调用户的残余信号,则接收端不能完美执行SIC 时,目标用户SINR 为:
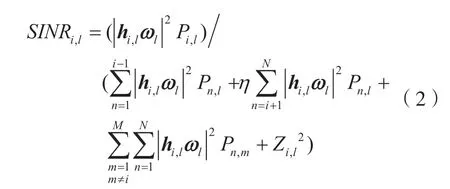
式中:η为不完美SIC 系数且η∈[0,1],η=0 表示接收端执行完美SIC,η=1 表示接收端不能执行SIC。
对于对间干扰,可以采用迫零波束赋形[20]设计的预编码矩阵消除,则目标用户的SINR 为:
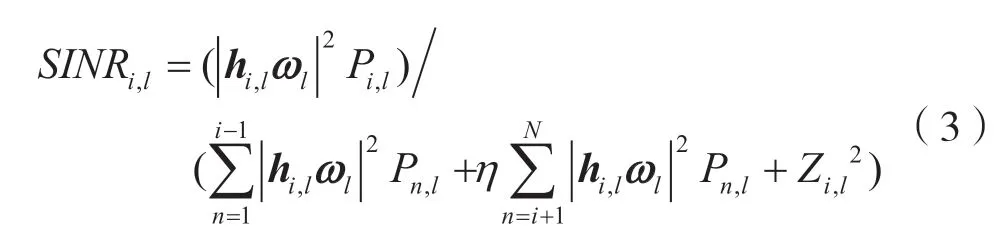
根据香农公式,NOMA 系统最大和速率优化问题为:
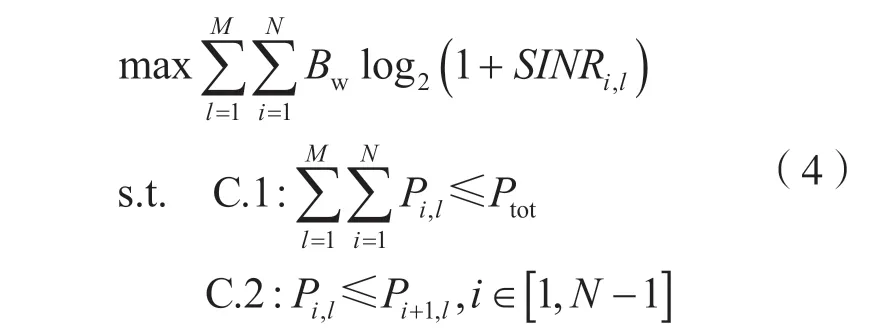
式中:Ptot为基站总发射功率;约束C.1 确保小区内用户分配的总功率小于系统总发射功率;约束C.2确保用户对中弱用户分配到的功率比强用户分配到的功率大。若用户配对方法已知,优化问题转化为求解最优功率分配矩阵问题;若功率分配矩阵已知,则转化为求解最优用户配对方案问题。但这两种情形下得到的均为非全局最优解。
2 用户配对和功率分配联合优化算法
考虑到用户配对问题的实质为组合优化问题,可用局部搜索算法求解,而功率分配问题为非凸问题,用连续凸逼近(Successive Convex Approximation,SCA)算法求解复杂度低,且其收敛结果与对应卡罗需库恩塔克(Karush-Kuhn-Tucker,KKT)条件极值点相同[21],提出JUPPA 算法,算法流程如图2所示。基于自适应遗传算法(Adaptive Genetic Algorithm,AGA)进行用户配对方案搜索,对AGA 算法中的每一个用户配对方案根据SCA 准则[22]和KKT 条件[22]进行功率分配优化,用寻优得到的功率分配系数矩阵计算适应度值,并依据计算得到的适应度值进行下一代种群的选择、交叉和变异。交替进行用户配对方案寻优和功率分配方案寻优,直至系统和速率收敛。
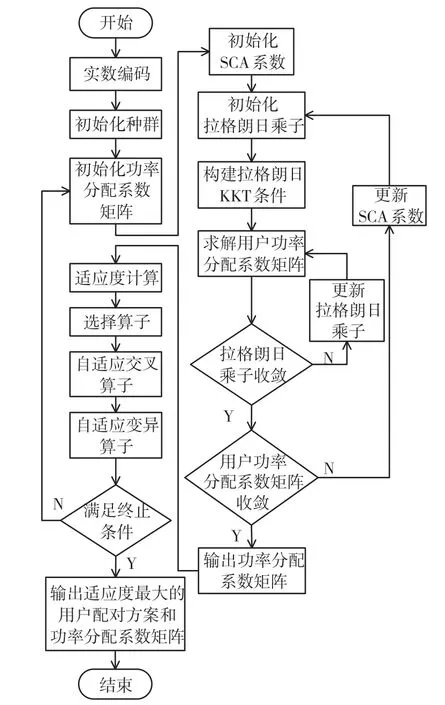
图2 用户配对和功率分配联合优化算法
2.1 用户配对
常规遗传算法(Genetic Algorithm,GA)[23,24]实现简单,但是容易陷入局部最优,并且设置交叉、变异概率过大会导致算法变成随机搜索,而设置交叉、变异概率过小会导致算法收敛过慢。针对常规GA 算法的不足,采用如图2 所示的AGA 算法进行用户配对方案搜索。使用自适应交叉和变异算子,根据种群适应度,自适应地调节交叉、变异概率,使算法更好地达到全局最优。同时,在交叉、变异生成新种群的过程中引入哈希表,避免产生重复的个体,提高算法的搜索效率。
2.1.1 编码策略
选用实数编码策略,便于直接在用户配对方案的表现型上进行交叉、变异操作。按照用户的生成顺序依次对用户进行编码,小区内用户的数量L即染色体的长度。
2.1.2 初始化种群
初始种群由Pop个长度为L的不重复染色体序列组成。按照染色体中基因序列的前后顺序,连续N个基因表示一个用户对,共组成M(M=L/N)个用户对,即形成一种用户配对方案。
2.1.3 选择算子
基于轮盘赌策略选择下一代种群中的父代,计算个体的适应度值在当前种群适应度的占比,即个体被选中作为父代的概率大小。适应度越高的个体,被选中作为父代的概率越大。
2.1.4 自适应交叉算子
从父代中随机选择两个染色体进行两点交叉,为了确保染色体中每个基因仅出现一次,对交叉后的染色体进行冲突检测,交叉概率随种群适应度值自适应变化,其表达式为:
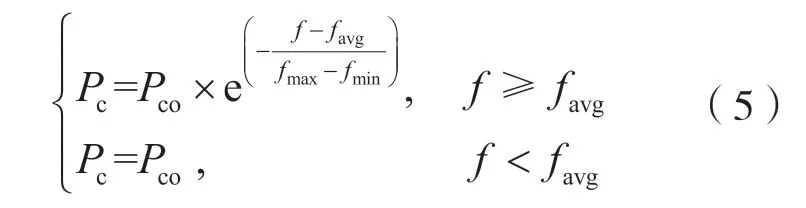
式中:fmax为当代种群中最大适应度值;fmin为当代种群中最小适应度值;favg为当代种群中平均适应度值;f为进行交叉操作的个体中较大适应度值;Pco为初始交叉概率;Pc为自适应变化的交叉概率。
2.1.5 自适应变异算子
在染色体内随机选择一个基因进行单点变异,即在染色体中随机选择两个基因交换。变异概率随种群适应度值的变化而变化,其表达式为:

式中:Pmo为初始变异概率;Pm为自适应变化的变异概率;f´为进行变异操作的个体的适应度值。
2.1.6 适应度计算
对于每个染色体,根据染色体表示的用户配对方案,结合当前的用户功率分配矩阵,计算系统和速率,作为其适应度值。
2.2 功率分配
最大化系统和速率是一个非凸混合整数规划问题[4],直接求解复杂度会随着约束条件和变量数呈指数增长。因此,通过拉格朗日乘子法和SCA 算法[21,22,25]求解最优功率分配系数矩阵。首先,使用SCA 算法对目标函数做凸处理;其次,使用拉格朗日乘子法构造KKT 条件,将有约束问题转化为无约束问题;最后,通过梯度下降法更新拉格朗日乘子。由收敛的拉格朗日乘子求解用户功率,用解得的用户功率进一步更新SCA 系数,直到拉格朗日乘子和用户功率同时收敛。
2.2.1 系统模型凸逼近
通过连续凸逼近方法,以原目标函数下界构造替代函数:
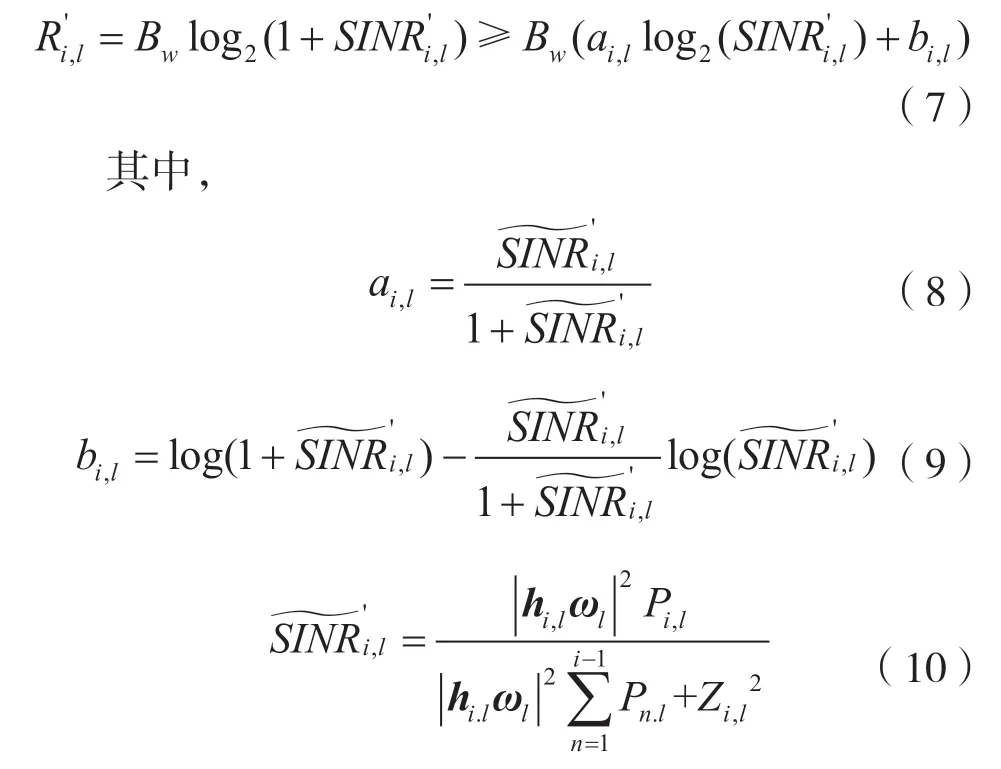
式中:R´i,l为用户对l中用户i的系统速率;a,b为SCA 系数;为辅助变量;SINR´i,l取最后一次迭代值。
这样,优化问题转换为:
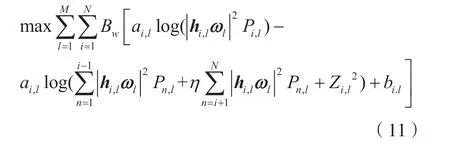
2.2.2 构建拉格朗日KKT 条件
由于式(11)目标函数仍为非凸函数,令Pi,l=eμi,l,将其转换为log-sum-exp 形式,可得:
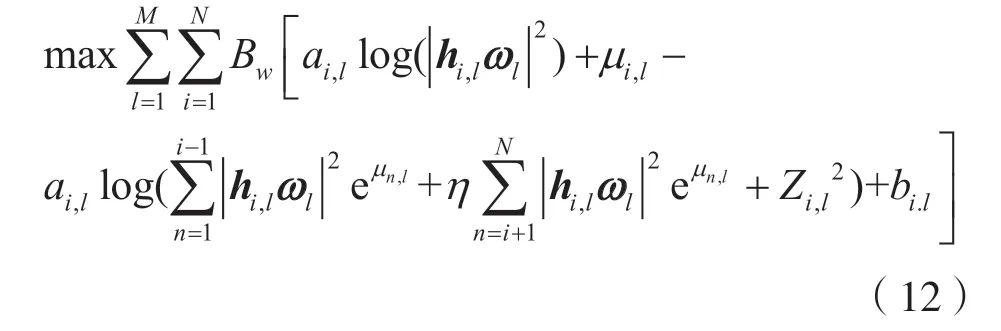
式中:μi,l为用户对l中用户i的功率值所对应的指数次方项。
同时,由于log-sum-exp 为凸函数[26],而约束条件也为凸函数,因此可以通过构造拉格朗日KKT条件来求解。
引入拉格朗日乘子v和ξi,l,将有约束问题转化为如下无约束求极值问题,即可求得用户功率。

对于拉格朗日乘子,采用梯度下降法进行迭代更新:

式中:t为迭代次数;φ和ψ为步长。功率分配算法的具体伪代码如下:

3 系统仿真
3.1 仿真参数设置
通过实验仿真对所提算法性能进行验证。在以基站为中心,半径为500 m 的蜂窝范围内生成随机独立分布的终端用户,设定用户数L=16。以NOMA方式进行用户复用,设定功率域叠加用户数N=2。无线信道为独立均匀分布的瑞利衰落信道。仿真参数设置如表1 所示。
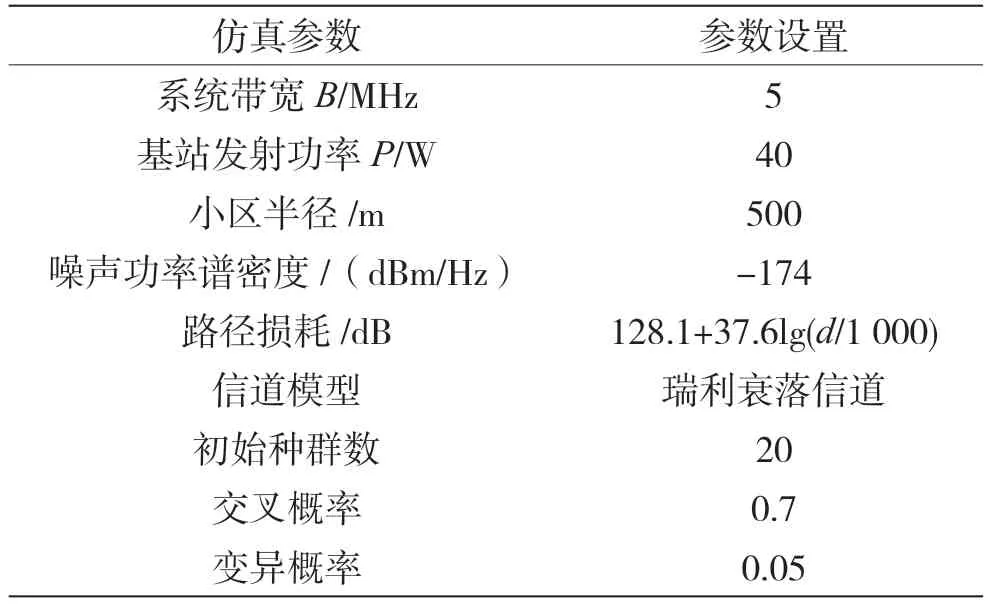
表1 仿真参数
3.2 仿真实验
3.2.1 不完美SIC 系数影响分析
为了研究不同程度干扰残留即接收端执行SIC能力对系统和速率的影响,设置不同的干扰残余系数η对JUPPA 算法进行仿真实验,结果如图3 所示。η=0 表示接收端执行完美SIC,即接收端不存在干扰残留,此时系统和速率最高。在用户信噪比相同的情况下,随着干扰系数的增加,系统和速率持续下降。这是由于在NOMA 系统中,干扰残余系数不会对弱用户的速率造成影响,但是强用户的SINR会随着干扰系数的增大而减小,导致强用户的速率降低,进而造成系统和速率下降。同时,当用户信噪比由10 dB 增加到40 dB,在η=0 时,系统有约10.5 Mbit/s 的和速率提升;η=0.01 时,系统和速率仅有约5.5 Mbit/s 的提升,说明当接收端存在干扰残留时,增大用户信噪比带来的和速率增益也会下降。当接收端执行串行干扰消除能力持续下降即干扰残留系数越来越大时,相比于正交多址接入(Orthogonal Multiple Access,OMA)系统,NOMA系统并不会带来系统和速率上的增益。当η=0.5 时,NOMA 系统和速率已明显低于OMA 系统和速率。

图3 不完美SIC 系数对系统和速率的影响
3.2.2 自适应遗传算法性能分析
将JUPPA 算法与常规GA 算法[24]和AGA 算法进行对比研究,仿真结果如图4 所示。可以看出,当接收端干扰残留系数相同,且GA 算法和AGA 算法使用相同功率分配算法时,两种算法均能求得最优的用户配对方案,达到基本一致的系统和速率性能。对比JUPPA 算法和AGA 算法,在使用相同用户配对算法的情况下,JUPPA 算法具有更高的系统和速率,说明在JUPPA 算法中,所提功率分配方案能带来更大的系统和速率增益。
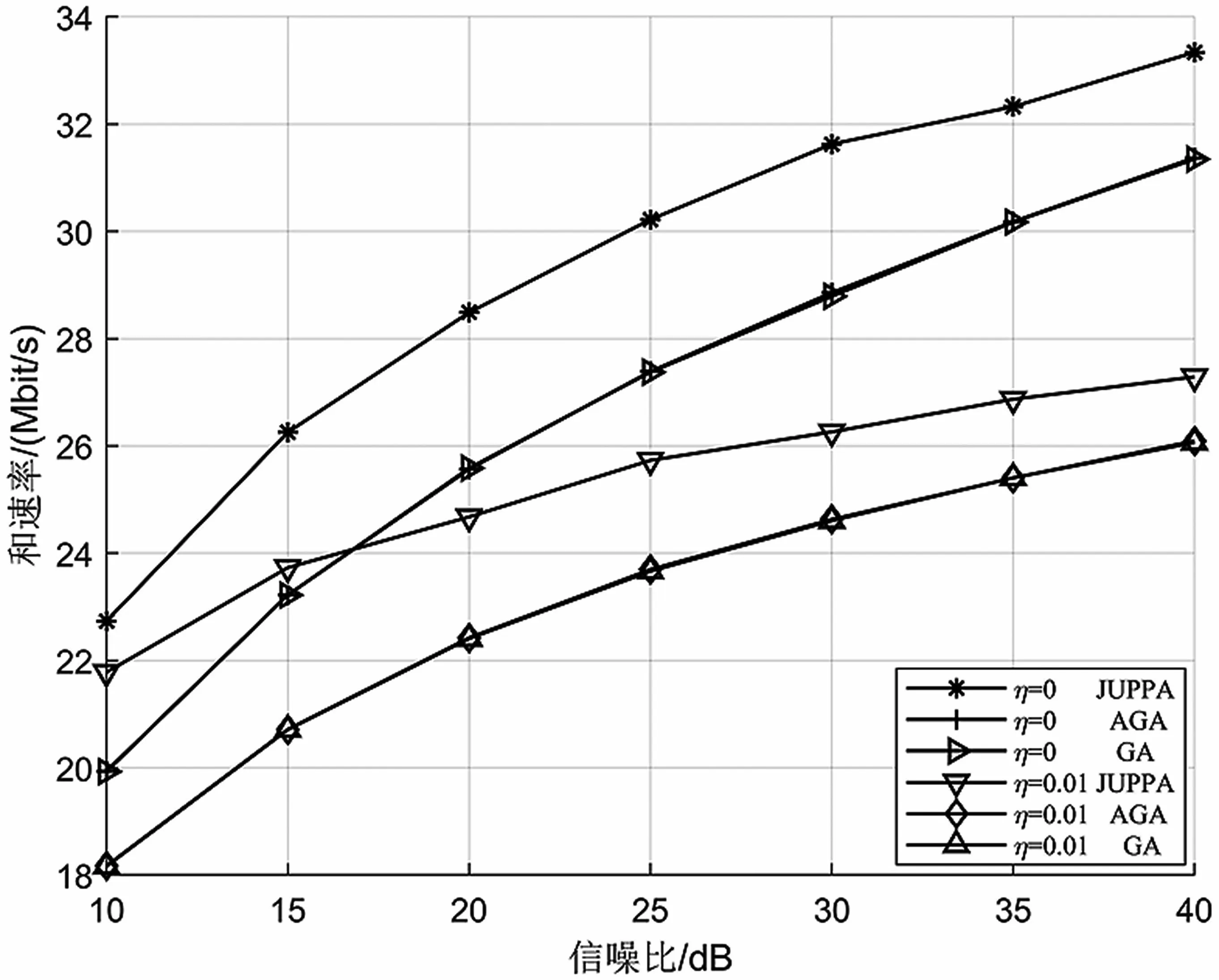
图4 JUPPA 算法、常规GA 算法和AGA 算法对比
然而,由图5 常规GA 算法和AGA 算法收敛对比可知,在基站发射功率、干扰残留系数相同的情况下,常规GA 算法在24 轮迭代后收敛,而AGA 算法在15 轮迭代即已接近于GA 算法收敛值,其后的和速率性能一直优于常规GA 算法。此外,22 轮之后的迭代,展现了AGA 算法跳出局部最优的强大能力。

图5 常规GA 算法和AGA 算法收敛性对比
3.2.3 与典型功率分配算法对比
将JUPPA 算法与当前代表性的功率分配算法,即固定功率分配(Fixed Power Allocation,FPA)算法[19]和分数阶功率分配(Fractional Transmit Power Allocation,FTPA)算法[10]进行对比研究,仿真结果如图6 所示。显然,在用户信噪比、干扰残余系数和用户配对方式均相同的情况下,JUPPA 算法具有更高的系统和速率,这是由于FPA 算法和FTPA算法仅按照信道增益进行功率分配。相比之下,JUPPA 算法考虑了干扰残留系数对系统和速率的影响,在确保NOMA 系统用户对中强弱用户功率分配原则下,干扰系数越大,会分配越多的功率给弱用户,由弱用户带来系统和速率上的提升。对比FPA算法和FTPA 算法,在用户配对方案相同的情况下,由于FTPA 算法能够动态地适应用户对中用户信道增益的变化,调整强弱用户之间的功率分配权重,因此FTPA 算法具有更高的系统和速率。

图6 JUPPA 算法与典型功率分配算法对比
3.2.4 与典型功率分配算法对比
将JUPPA 和代表性的用户配对算法,即随机用户配对(Random Pairing Algorithm,RPA)算法[3]和基于最大信道增益差的传统NOMA 配对(Conventional NOMA,C-NOMA)算法[7]进行对比研究,仿真结果如图7 所示。可见,相同功率分配算法下,JUPPA 算法拥有比RPA 算法和C-NOMA算法更高的系统和速率。这是由于JUPPA 算法使用AGA 算法在用户配对组合方案中进行搜索,而RPA 算法未考虑用户之间信道增益差异,C-NOMA算法则未考虑用户间的信道增益近零问题。RPA 算法的和速率性能仅优于OMA 系统,因为在NOMA系统中将具有一定信道增益差的用户进行配对就能产生一定的系统和速率增益,使得NOMA 系统的和速率优于OMA 系统。同样,对比不同干扰残留系数下的OMA 系统和速率,由于OMA 系统不存在功率域的复用,即不涉及用户配对,也就并不存在干扰残留的问题,故不同干扰残留系数的OMA 系统和速率曲线完全一致。
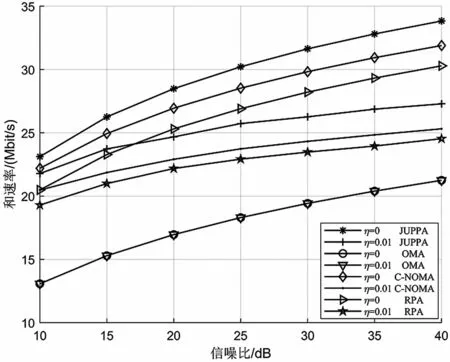
图7 JUPPA 算法与典型用户配对算法对比
4 结语
本文针对不完美SIC 下的NOMA 系统和速率优化问题,提出了一种联合用户配对和功率分配的优化算法JUPPA。在用户配对阶段,设计了AGA 算法进行用户配对方案寻优;在功率分配阶段,采用SCA 准则和KKT 条件求解最优功率分配系数矩阵。仿真结果表明,接收端执行SIC 的能力强弱,对系统和速率有着较大影响,同时,JUPPA 算法中AGA算法相比常规GA 算法具有更高的收敛速度和更优的全局搜索能力,且与已有用户配对和功率分配算法对比,JUPPA 算法具有更高的系统和速率。对于考虑不完美SIC 的NOMA 系统研究,本文具有一定的参考意义。
