高效可撤销的共享数据云存储审计①

仪张倩,温琳雅,张维鑫

(长安大学 信息工程学院,西安 710064)

近年来,云计算[1]作为一种新的计算模型,吸引了人们的广泛关注.云存储作为云计算的重要组成部分,已经被人们以极大优势频繁地用于存储数据.比如,数据所有者不再需要处理大量的数据,无论数据使用者所处何地,查阅资料都很方便.由于云存储有很多优势,越来越多的用户选择将他们的数据存储在知名的云服务器(CSP)上.例如,大家所熟知的谷歌、微软等大型网络公司均有云存储的服务;在国内,百度云和微云则是市场占有量最大的存储云.此外,通过CSP 提供的数据存储和共享服务,使人们可以很轻松地进行团队合作.更具体地说,一旦用户在云端创建了共享数据,用户群内的每个用户不仅可以访问和修改共享数据,还可以与群内其他人共享最新版本的数据.虽然数据存储和共享服务使数据所有者可以方便地访问、修改和共享用户群内的数据,以致用户从这种数据管理方式中受益匪浅,但是数据外包到云上进行存储的方式也引发了严重的安全问题.首先,一旦用户数据被外包到CSP 上,用户失去了对数据的直接控制权[2],这使得用户担心CSP是否正确地存储了用户数据.例如,CSP 可能由于软件或者硬件故障[3,4]遭受内部敌手或者外部敌手的攻击.其次,恶意的CSP 可能删除极少被访问的数据以节省存储空间或者掩盖数据被损坏的事实以维持自身的良好声誉.因此,如何保证用户外包数据的完整性[5-8]是至关重要的问题之一.

为了解决数据完整性问题,一些基于传统密码学的公开审计方案[5,9,10]被提出.其中,用户的公、私钥是通过数字证书发放,通信效率低,计算量大,证书的管理成本高.为了解决复杂的证书管理问题,Shamir 等人[11]引入基于身份的密码体制概念.在基于身份的密码体制中,用已知的身份信息作为公钥,来避免使用公钥证书.之后,基于身份的可证明数据拥有方案[12-18]被提出,但是这些方案[12-18]大多利用双线性对技术和映射到点的哈希函数来实现完整性认证,需要昂贵的时间和通信成本,造成很大的计算和存储负担.

为了在实现数据共享服务的同时,高效实现用户可撤销,本文提出了一种高效的隐私保护可证明数据拥有方案.首先,所提方案采用基于椭圆曲线密码学[19,20]实现了无对认证,并且不使用映射到点的哈希函数,极大地减少了通信和计算代价[21,22].其次,所提方案采用中国剩余定理[23]实现了高效安全的用户撤销[24,25],在实现隐私保护的同时,保证方案的高效性.最后,在设定的实验模型下,给出了所提方案的计算和通信成本分析,证明所提方案的效率高于已知方案[15-17].

1 背景知识

1.1 椭圆曲线

椭圆曲线密码学的概念是由Miller[19]和Koblitz[20]基于椭圆曲线提出.定义Fp是阶为素数p的有限域,则Fp上的椭圆曲线E上所有的点(x,y) 满足等式y2=x3+a·x+bmodp,其中4a3+27b2≠0且a,b∈Fp.椭圆曲线E上的无穷远点O与其他点构成一个循环加法群 G,群G的阶为q,G 生成元为P.群 G 上的标量乘法是θP=P+P+···+P(θtimes),这里θ ∈Z*q.

1.2 中国剩余定理

中国剩余定理[23]是一种古老的求解相同余数的方法,它是数论中的重要定理.设定k1,k2,···,kn互为素数,计算以及 βi满足Mi×βi≡1 modki.对于整数var1,var2,···,varn,计算α=vari·Mi·βimodM,以下方程组成立:

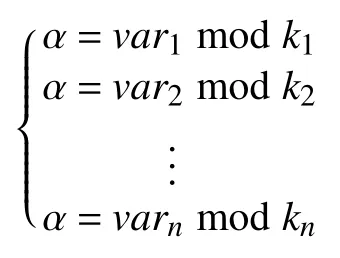
1.3 困难问题及假设

(1)椭圆曲线离散对数问题(ECDL 问题):假定G是一个加法群,P是G的生成元,给定元组(P,a·P∈G),这里a∈Z*q且未知,ECDL 问题是计算a∈Z*q.

(2)椭圆曲线离散对数(ECDL 假设):任何概率多项式时间算法都不能以不可忽略的概率解决ECDL问题.

(3)计算性Diffie-Hellman 问题(CDH 问题):假定G1是一个循环加法群,P是G1的生成元.给定元组(P,a·P,b·P∈G1),这里a,b∈Z*q未知,CDH 问题就是计算a·b·P.

(4)计算性Diffie-Hellman 假设(CDH 假设):概率多项式时间算法都不能以不可忽略的概率解决CDH问题.

1.4 系统模型

所提方案的系统模型图,如图1所示.其中,共有5 个参与者,包括密钥生成中心(KGC),车辆用户(Ui(i=1,2,···,n)),路边单元(RSU),第三方审计者(TPA)和云服务器(CSP).

图1 系统模型图

(1)RSU:路边单元,是具有足够计算能力的雾设备,可以及时处理每个车辆用户的传感器产生的信息,并将其上传到CSP.在本文中看作车辆用户群的群管理者GM,后续内容不再赘述.

(2)Ui(i=1,2,···,n):车辆用户.n个 车辆用户Ui组成一个车辆用户群,由群管理者GM (即RSU)为其分发私钥和上传数据.每个车辆用户Ui都可以通过云储存与其他用户共享数据.离开的用户不能上传数据或者通过云存储访问共享数据.

(3)KGC:密钥生成中心,是一个完全可信的参与者,具有强大的计算和存储能力,负责初始化整个系统以生成主密钥和公共参数,并且为用户群生成和分配群私钥.

(4)CSP:云服务器,是一个半可信实体,具有强大存储空间和计算能力.云服务器在接收到第三方审计者发来的审计请求时,为第三方审计者生成相应的审计证据.所有数据都存储在云服务器中,所有的用户通过云服务器实现数据共享服务.

(5)TPA:第三方审计者,作为一个半可信的实体,接受用户群的审计委托,向云服务器发送审计询问,并根据云服务器返回的证据确定共享数据是否完整存储在云服务器中.

1.5 安全需求

作为一个基于身份的共享数据云存储审计方案,需要满足下面的安全需求:

公开审计:TPA 能够代表用户认证CSP 中存储的数据的完整性.

存储正确性:如果用户,TPA和CSP 都是诚实的,并且正确地执行了指定的算法,那么CSP 生成的证据能够通过TPA的完整性认证.

安全用户撤销:确保被撤销的用户无法像CSP 上传数据和数据标签.

数据隐私保护:TPA 在审计阶段不能获得CSP 中存储的任何数据.

2 本文方案

方案由7 个算法组成,包括系统建立算法,密钥生成算法,标签生成算法,挑战生成算法,证据生成算法,证据认证算法,和用户撤销算法.

2.1 系统建立算法

由KGC 执行,输入安全参数 ξ,输出系统参数params和主密钥msk.

(1)给定一个安全参数ξ,基于定义在有限域Fp上的椭圆曲线E,选择一个阶为q的群G,并且群G的生成元为P.

(2)随机选择s∈Z*q,计算Ppub=s·P.

(3)选择密码学安全的哈希函数:h1:{0,1}*→Z*q,h2:{0,1}*→Z*q.

KGC 保存主密钥msk=s,公开系统参数params={q,P,G,Ppub,h1,h2,ψ,π}.

2.2 密钥生成算法

由KGC,群管理者GM和合法的车辆群用户Ui(i=1,2,···,n)执行:

(1)在接收到GM的身份ID后,KGC 随机选择rID∈Z*q,计算RID=rID·P,skID=rID+s·h1(RID||ID).KGC 设置(skID,RID)为身份密钥,并将其发送给GM.

(2)GM 接收到(skID,RID)之 后,认证等式skID·P=RID+Ppub·h(RID||ID)是否成立.如果成立,接受身份私钥(skID,RID);否则,拒绝它.

(3)GM 随机选择,ki∈Z*q(i=1,2,3,···,n) 计算S=计算yi以满足xi×yi≡1 modki,并计算

(4)GM 随机选择skGM∈Z*q作为n个用户的部分私钥,计算pkGM=skGM·P.GM 计算车辆群用户私钥sk=skID+skGM和W=sk·w=并将ki(i=1,2,···,n) 以秘密信道发送给每个车辆群用户Ui,将W||S igmsk(W)以公开信道发送给每个合法的车辆群用户Ui.

(5)每个Ui接收到W||S igmsk(W)之后,认证S igmsk(W)的有效性.如果认证失败,Ui回复“拒绝”,算法终止;否则,合法的群用户Ui可以分解出W,并计算Wmodki=sk,得到群私钥sk.

2.3 标签生成算法

给定原始文件F,Ui执行:

(1)将原始文件F分为n个块,得到F={m1,m2,···,mn},且mi∈Zp,i∈{1,2,···,n}.

(2)对于每个i∈{1,2,···,n},随机选择ri∈Z*q(i=1,2,3,···,n),计算Ri=ri·P,σi=ri·mi+sk·h2(IDF||pkGM||RID||Ri),这里IDF表示文件标识符,i表示文件第i个数据块的索引标识符,pkGM和RID为用户群公钥.

Ui生成文件标签σ={(σi,Ri)}i∈[1,n],上传至CSP.

2.4 挑战生成算法

当收到来自Ui的审计请求之后,由TPA 执行:

随机选择k1,k2∈Z*q,c∈[1,n],生成挑战消息chal={c,k1,k2},将其发送给CSP.

2.5 证据生成算法

在接收到来自TPA的挑战消息之后,由CSP 执行:

(1)计算vj=ψk1(j),wj=πk2(j),1≤j≤c,得到Q={vj,wj}1≤j≤c.

2.6 证据认证算法

给定proo f={a,b},由TPA 执行:

(1)对于所有的j∈Q,计算H(IDi‖pk‖Ri),认证等式a=是否成立.

(2)如果等式成立,说明CSP 正确存储了用户的数据,发送“成功”给Ui;否则,发送“失败”给Ui.

2.7 用户撤销算法

当用户群内有用户离开或者由于不合法的行为被撤销时,由群管理者GM和合法群用户执行:

(1)当用户Ui从用户群 U中撤销时,GM 计算w′=w-wi.

(2)GM 选择一个新的部分私钥skG′M∈Z*q,并计算其对应的公钥pkG′M=skG′M·P,车辆群用户私钥sk′=skID+skG′M和W=sk′·w′,生成更新密钥的消息W′=sk′×w′,并将其以公开信道发送给每个合法的车辆群用户Ui.

(3)车辆群用户Ui接受到更新密钥的消息W=sk′·w′之后,计算W′modki=sk′,即可以得到新的群私钥sk′.

3 方案分析

3.1 方案正确性分析

由所提方案可知,如果TPA和CSP 都是诚实的,并且正确地执行了指定的算法,且proof={a,b}满足下列等式成立,那么所提方案是正确的.

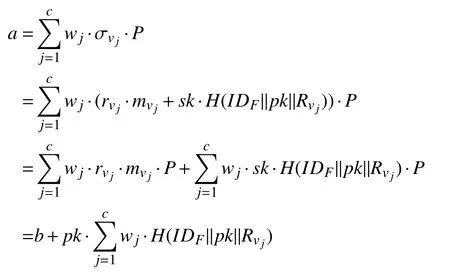
由于等式成立,因此,所提方案是正确的.

3.2 方案安全性分析

(1)公开审计:所提方案中,TPA 能够代表用户对CSP 发起审计挑战,并且可以通过系统公开参数,用户群的公钥pk和挑战消息chal={c,k1,k2},对来自CSP的审计证据的正确性进行认证.

(2)存储正确性:通过对方案的正确性分析,我们得到,如果用户,TPA和CSP 都是诚实的,并且正确地执行了指定的算法,那么CSP 生成的证据能够通过TPA的完整性认证.

(3)安全的用户撤销:每当有群用户离开,新的群用户加入和不合法的群用户被撤销时,都生成新的用户群私钥sk′.因此,除了KGC和合法的群用户之外,被撤销的群用户,没有加入的群用户和不合法的用户不可能得到新生成的私钥的任何消息,无法上传用户数据和相应的标签.

(4)数据隐私保护:在TPA 对CSP 进行审计的过程中,TPA 不能从proof={a,b}中得到存储在CSP 中消息的任何内容,这里Rvj.首先,TPA 尝试对b求解得到数据消息mvj,但是由于Rvj=rvj·P,这相当于解ECDL 问题.因此,TPA 不能从b中得到有关数据消息mvj的任何内容.其次,TPA 尝试对a求解得到数据消息mvj,但是由证明得到,由于我们不能解ECDL 问题,因此,无法得到有关数据消息mvj的任何内容.综上所述,所提方案满足数据隐私保护.

3.3 计算代价分析

为了满足80 bit的安全性,对于现存方案[15-17],选择双线性对e:G1×G1→G2,群 G1的阶为p,p是512 bit的素数.对于所提方案,选择椭圆曲线上的加法群 G,群 G的阶为q,q是160 bit的素数.基于C++MIRACL Crypto SDK 库[26],仿真实验在CPU为英特尔i5(2.53 GHz),内存为4 GB的64 位Windows 10 操作系统下进行.表1给出了相关密码操作运行10 000 次的平均时间.表2给出了已知方案[15-17]和所提方案计算代价的比较.

表1 密码运算的运行时间

表2 计算代价对比

图2-图4分别表示标签生成阶段,证明生成阶段和证据认证阶段的计算代价比较.正如图2-图4显示,所提方案的计算代价明显低于已知方案[15-17].并且,随着文件块数量n的增加,所提方案的优势更加明显,具体原因如下.首先,由于已知方案[15-17]的完整性认证是基于双线性对技术,因此,已知方案[15-17]大多使用群G1下的标量加法运算,群 G1下的标量乘法运算,映射到点的哈希函数运算和双线性对运算.其次,由于所提方案的完整性认证是基于椭圆曲线技术,因此,所提方案大多使用群 Z*q下的标量加法运算,群 Z*q下的标量乘法运算,ECC 下的标量加法运算,ECC 下的标量乘法运算和普通哈希运算.此外,由表1可得,群 G1下的标量加法和乘法运算远远大于群 Z*q和ECC 下的标量加法和乘法运算,映射到点的哈希运算远远大于普通哈希运算,并且双线性对运算花费很大的计算和通信成本.因此,所提方案的计算代价明显低于已知方案[15-17].

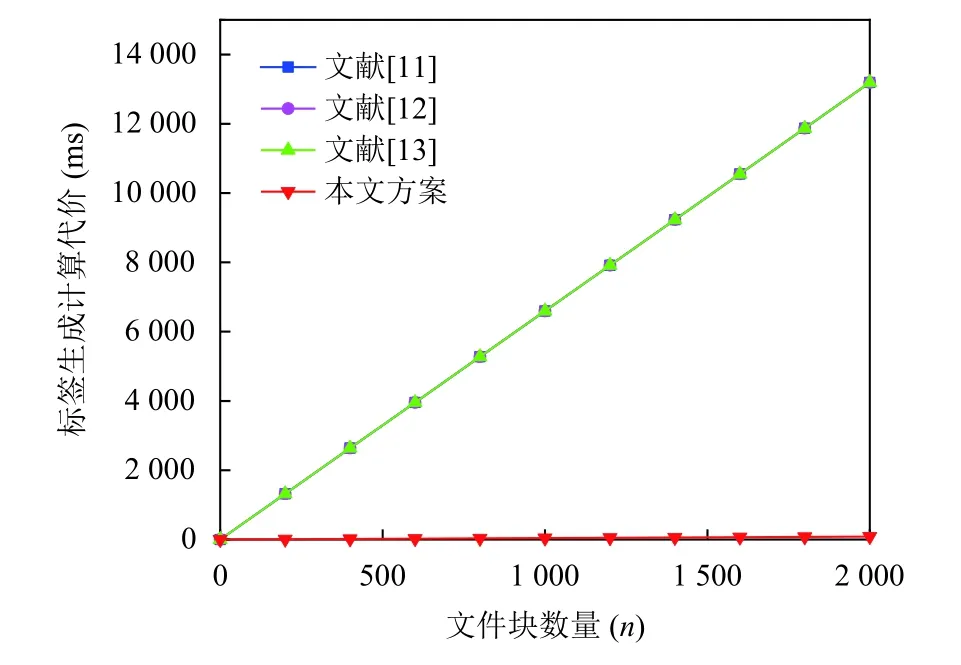
图2 标签生成的计算代价比较

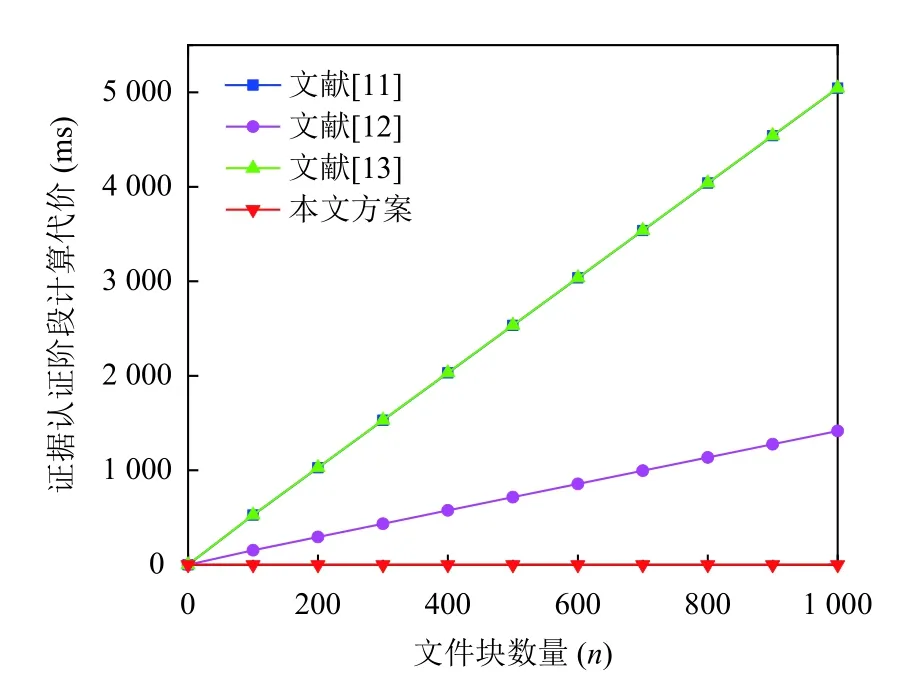
图4 证据认证的计算代价比较

3.4 通信代价分析

为满足80 bit的安全性,|G1|,| Z*q|,| G|,|n|分别为512 bit,160 bit,160 bit和32 bit.通信代价主要讨论从TPA 到CSP 挑战信息和从CSP 到TPA的响应信息.表3展示了本方案与现存方案[15-17]在通信代价方面的比较.

图3 证据生成的计算代价比较

如表3所示,首先,从TPA 到CSP,现存方案[15-17]有相同的1 92×cbit的通信代价.显然,从TPA 到CSP,随着挑战块数量的增加,现存方案的通信代价线性增加,而所提方案的通信代价保持不变,保持 4 80 bit的通信代价.因此,在挑战生成阶段,所提方案的通信代价明显低于已知方案[15-17].

表3 通讯数据对比 (bit)

其次,从CSP 到TPA,现存方案[15-17]的通信代价都保持不变,分别为1 184 bit,672 bit,672 bit,320 bit.因此,在证据生成阶段,所提方案的通信代价明显低于已知方案[15-17].

4 结论与展望

为了解决复杂的证书管理问题,一些基于身份的可证明数据拥有方案被提出.但是,这些方案大都采用昂贵的双线性对运算和映射到点的哈希函数,具有很大的通信和计算代价.本文采用椭圆曲线技术和中国剩余定理技术提出了一种高效的隐私保护可证明数据拥有方案,在保证方案隐私和效率的同时,实现了高效安全的用户撤销.安全性分析表明,所提方案能够满足基于身份的可证明数据拥有方案的安全需求.计算代价和通信代价的分析表明,与现存方案[15-17]相比,所提方案具有较低的通信和计算代价.在本文的基础上,可进一步研究用户如何以更低的代价将数据和标签上传到多个CSP 上,以及防止如何进一步防止CSP和TPA的合谋攻击.