基于Euler-Maruyama法的微分方程数值解的收敛性研究

2022-05-10宋丽雅

哈尔滨师范大学自然科学学报 2022年1期

宋丽雅

(长治幼儿高等师范专科学校；太原师范学院)

0 引言

自变量分段连续型微分方程(SEPCAs)是一类可以应用到生活中各个领域中的微分方程，这类方程可以被应用在表示理学、工学、医学等领域的一些模型中[1].SEPCAs方程的解是一个不间断的，在相邻的两个区间的端点上的解具有递推关系[2].SEPCAs方程的解一般以初始数据有限集合表示，随着数据集的变化方程解也随之变化，而不是如微分方程那样以初始函数进行判断[3].描述方程的每一个独立区间都可以构成一个离散自变量的差分方程，能够用于描述事物变化的规律[4].所以，SEPCAs方程代表了具有连续性和离散动力系统的融合，通过解析可以反映微分与差分方程二者的关系[5].例如，信号控制系统中的脉冲传递数学模型X′(T)=aX(T)+VX(|t|),t>0属于自变量分段连续微分方程[6].因此，无论在理论上还是应用上，对SEPCAs的分析都是一个有趣的调研方向.通常情况下，自变量分段连续型随机微分方程是无法求出方程的显式解的，所以在现实求解中需要求出数值解[7].该文研究SEPCAs方程的数值解和SEPCAs数值解的收敛性，为SEPCAs方程数学模型的应用提供参考.

1 基础符号和欧拉方法

1.1 基础符号

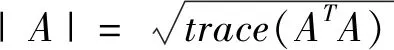
1.2 自变量分段连续型随机微分方程

在本文中，考虑了自变量分段连续型随机微分方程：

dx(t)=f(x(t),x([t]))dt+

g(x(t),x([t]))dB(t),∀t≥0

(1)

带有初值x(0)=x0，其中f:Rn×Rn→Rn，

g:Rn×Rn→Rn×d，[x0]为矢量，[·]表示取整函数.根据随机微分的定义，式(1)基本可以相当于下列的随机积分方程：

(2)

除此之外，还要求系数f和g足够光滑.确切地说，给出了下列条件：

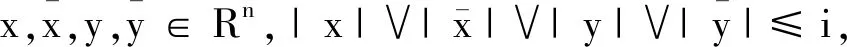
(3)

(H2)线性增长条件：存在一个正常数K，使得

|f(x,y)2|∨|g(x,y)2|≤K(1+|x2|+|y2|)

(4)

(H3)单调条件：对于所有的(x,y)∈Rn×Rn，一般情况下都存在一个正常数K1，可以令

|x2|+|y2|)

(5)

(H4)有界p阶矩条件:存在一对常数p>2和K2，使得

(6)

如果一个Rn值随机过程具有以下三条性质，则称其为方程(1)在[0,∞)上的解[6]：

(1){x(t)}在[0,∞)上是连续的，Ft是可适应的；

(2){f(x(t),x([t]))}∈L1([0,∞),Rn)且{g(x(t),x([t]))}∈L2([0,∞),Rn×d)；

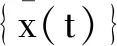
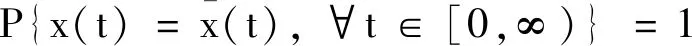
(7)

yn+1=yn+f(yn,yh([nh]))h+

g(yn,yh([nh]))ΔBn

(8)

对于n=0,1,2,…，其中ΔBn=B(tn)-B(tn-1)，yh[nh]是精确解x([nh])的近似值.设n=km+l(k=0,1,2,…,l=0,1,2,…,m-1)，欧拉方法对方程(1)的可适应导致了以下类型的数值过程

ykm+l+1=ykm+l+f(ykm+l,ykm)h+

g(ykm+l,ykm)ΔBkm+l

(9)

其中ΔBkm+l=B(tkm+l)-B(tkm+l-1)，ykm+l和ykm分别是精确解x(tkm+l)和x([tkm+l])的近似值.连续Euler-Maruyama 近似解被定义为

(10)

其中对于t∈[tkm+l,tkm+l+1]有，z(t)=ykm+l和z([t])=ykm.不难看出对于k=0,1,2,…，l=0,1,2,…,m-1有y(tkm+l)=z(tkm+l)=ykm+l.对于足够大的整数i，定义停止时间ηi=inf{t≥0:

|x(t)|≥i},θi=inf{t≥0:|y(t)|≥i},τi=ηi∧θi.

2 Euler-Maruyama方法的收敛性

2.1 Euler-Maruyama方法在p阶矩有界条件下的收敛性

引理1 在(H1)条件下，设T>0是任意的，有

Esup|y(t)-z(t)|2≤C1(x0,i)h

(11)

其中C1(x0,i)=4Li(T+4)K2.

证明对于t∈[0,T)，存在着两个整数，分别为k和l，进而使得t∈[tkm+l,tkm+l+1].通过Hölder不等式，便不难可以推断出

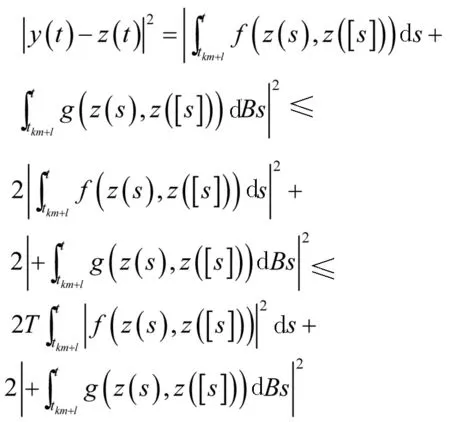
这也就是说，对于任意的0≤t1≤T

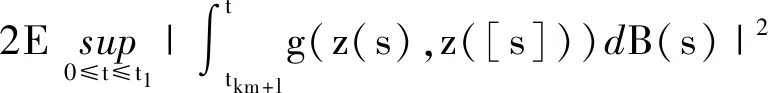
通过Doob’s鞅不等式，可以得到

利用局部Lipschitz条件

C1(x0,i)h

其中C1(x0,i)=4Li(T+4)K2.

定理1 在(H1)条件和(H4)条件下，Euler-Maruyama近似解收敛于方程(1)的精确解

(12)

证明首先确定p>2；再设e(t)=x(t)-y(t)；因此，很容易能够看出

因此，对于任意δ>0，有

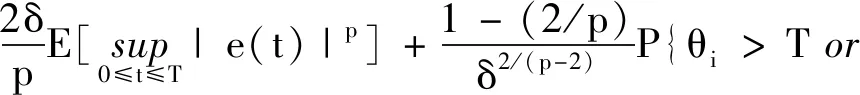
ηi>T}

由条件(H4)，可以得出

P(θi≤Torηi≤T}≤P(θi≤T)+

使用下面的两个界限

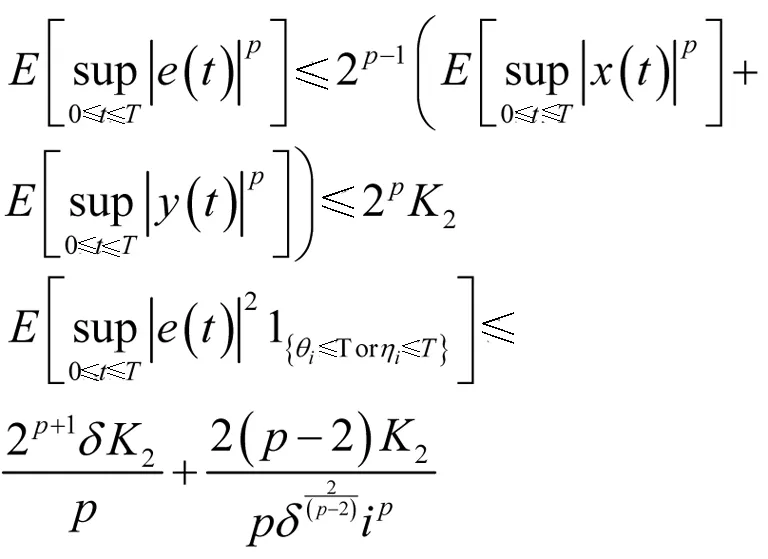
通过这些x(t)和y(t)的定义，有

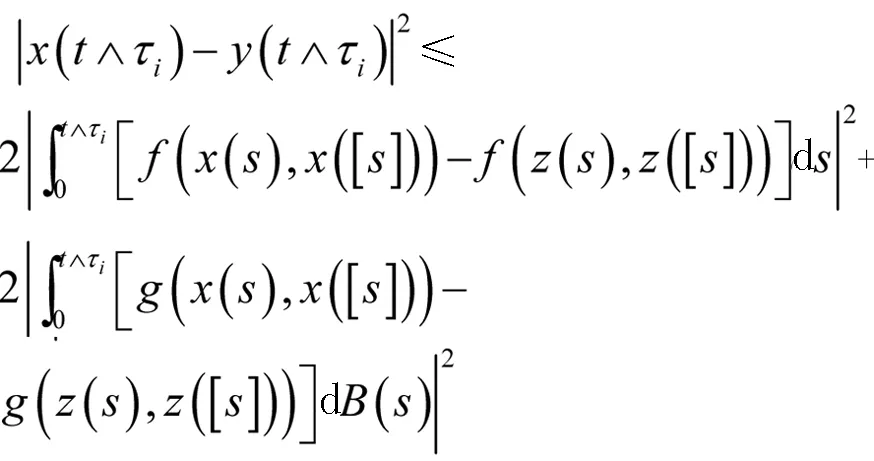
因此，对于任意t1∈[0,T]

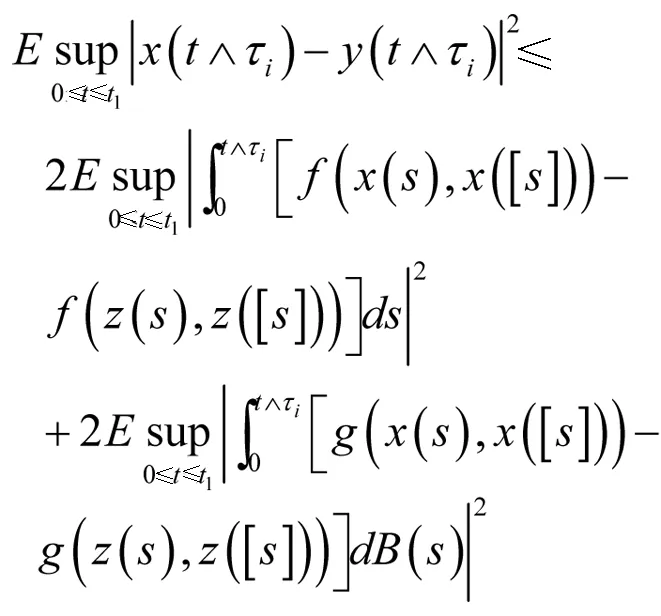
(13)

根据Hölder不等式，条件(H1)和引理1，可以得到

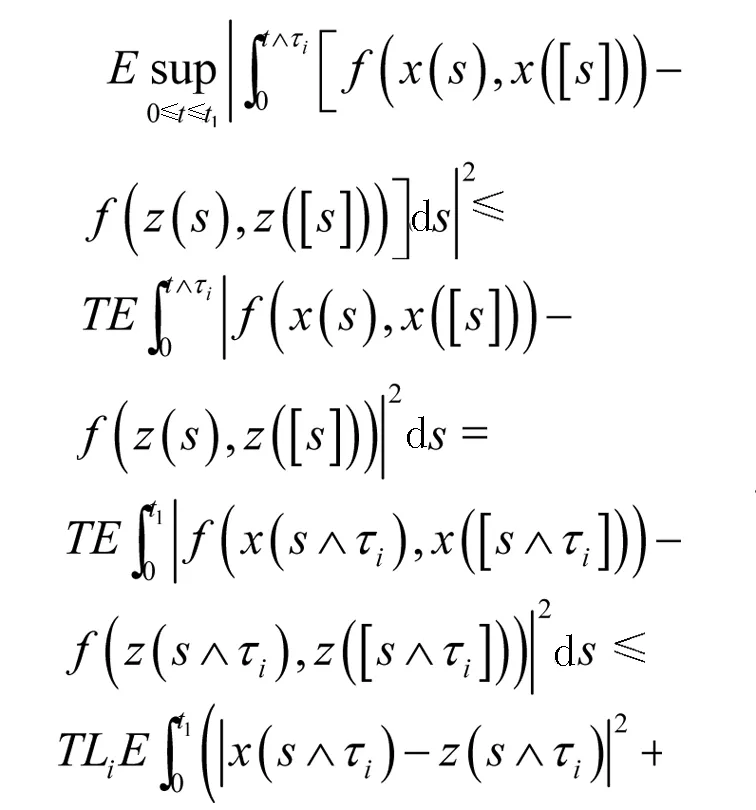
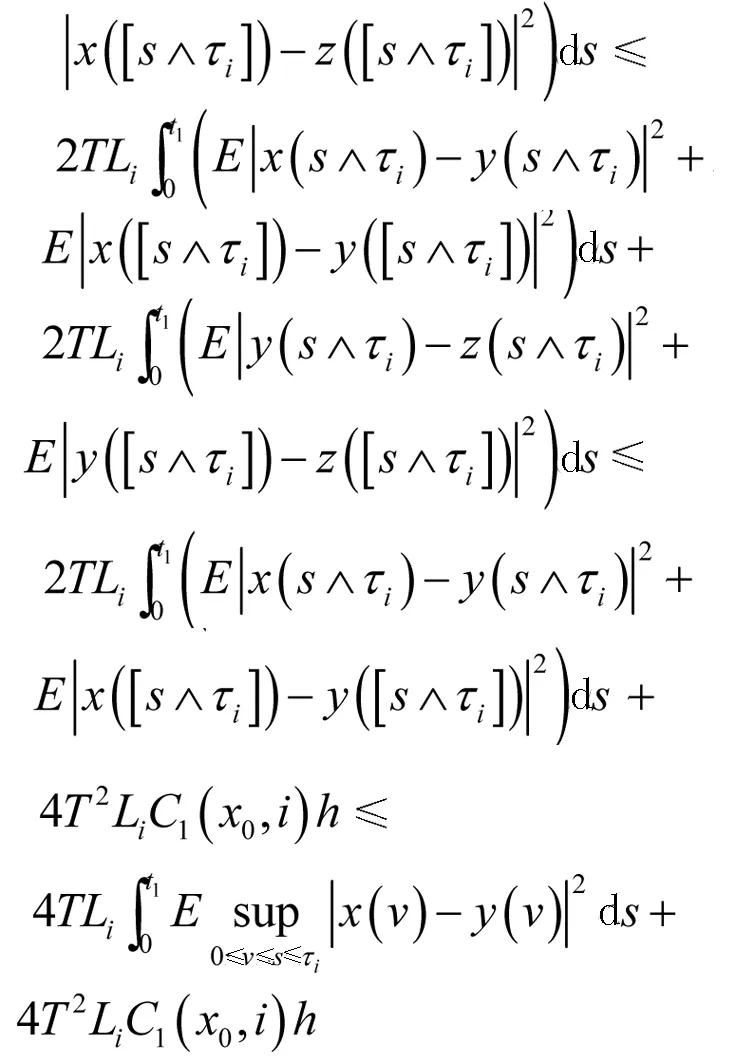
(14)

(15)

把式(14)和式(15)共同代入到式(13)中可以得出

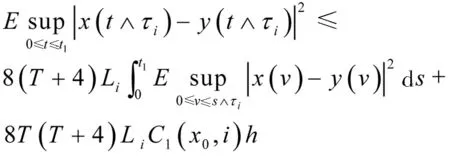
通过Gronwall不等式，必然可以得到

Esup|x(t∧τi)-y(t∧τi)|2≤

C2(x0,i)h

其中C2(x0,i)=8T(T+4)LiC1(x0,i)e8T(T+4)Li，有

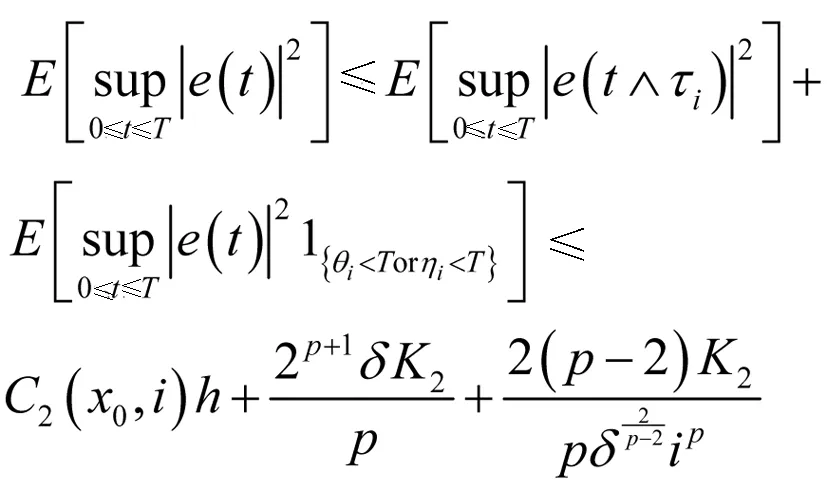
2.2 Euler-Maruyama方法在线性增长条件下的收敛性

引理2 在线性增长条件下(H2)，存在一个正的常数C3，能够让方程(1)的解满足

(16)

其中C3=C3(p,T,K)是一个与h无关的常数.

证明由式(2)可知

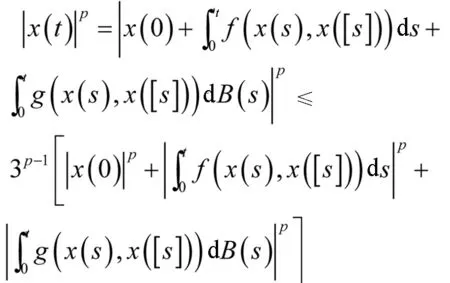
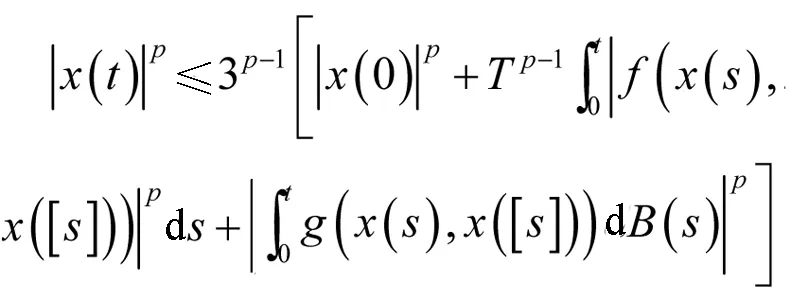
这就意味着，对于任意0≤t1≤T有，

接下来，通过Burkholder-Davis-Gundy不等式以及Hlder不等式，可以很容易看出

其中Cp是一个常数，由线性增长条件可知

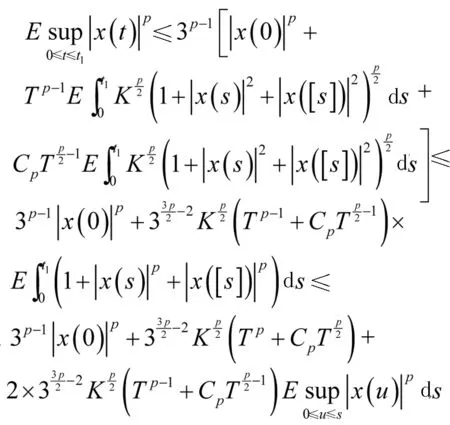
通过Gronwall不等式，可以得到

其中C3=C3(p,T,K)是一个与h无关的常数.

2.3 单调条件下Euler-Maruyama方法的收敛性

引理3 在单调条件(H3)下，存在一个正的常数C5，使得方程(1)的解可以满足

(17)

其中C5=C5(p,T,K1,x0)是一个与h无关的常数.

证明通过It公式，对于所有的t≥0，都有

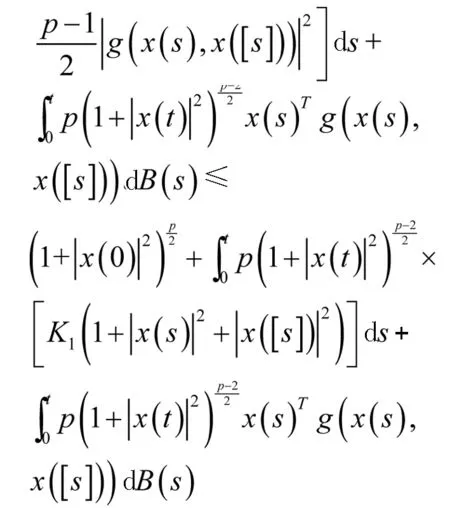
对于任意的t1∈[0,T]，有

通过Burkholder-Davis-Gundy不等式可以得到

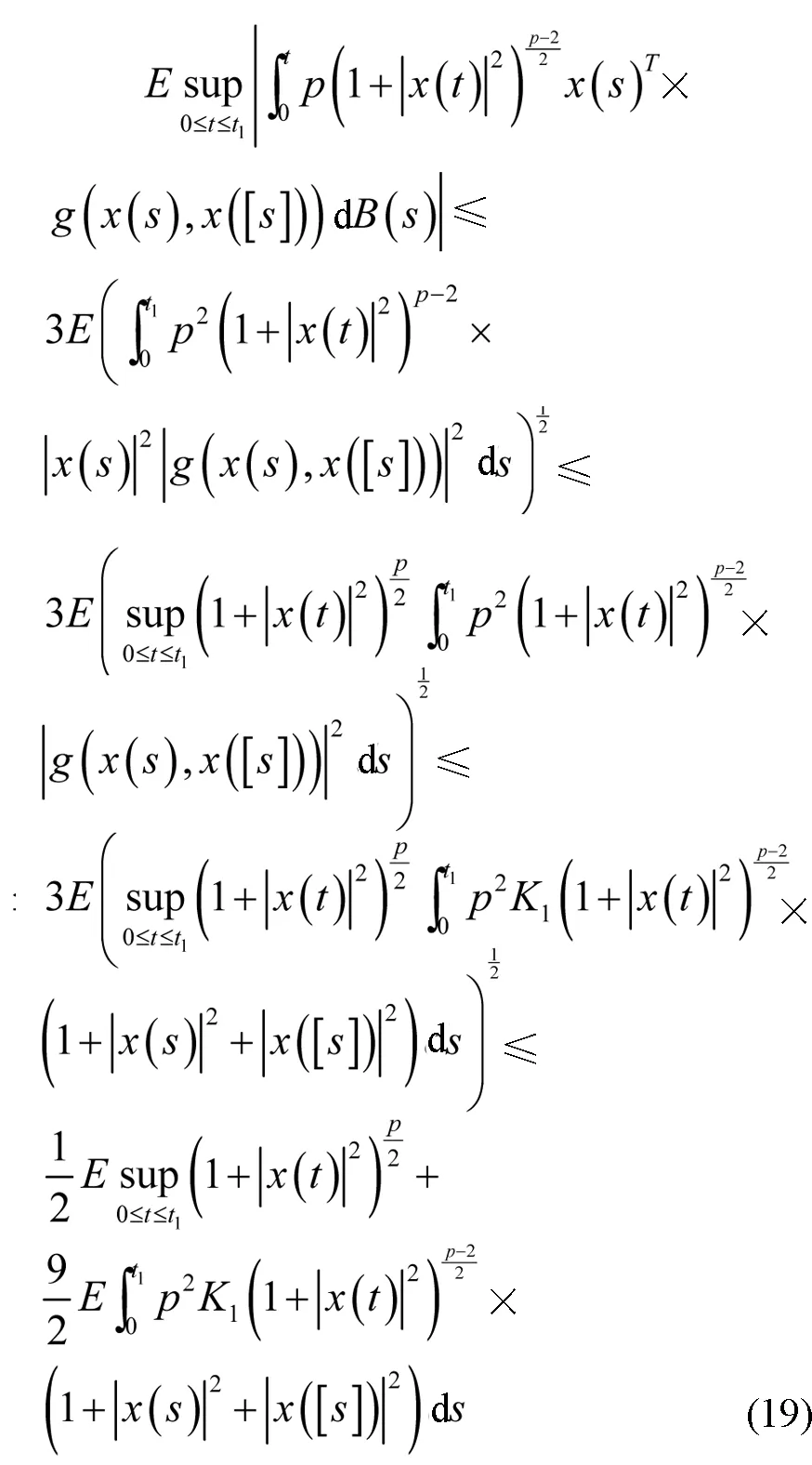
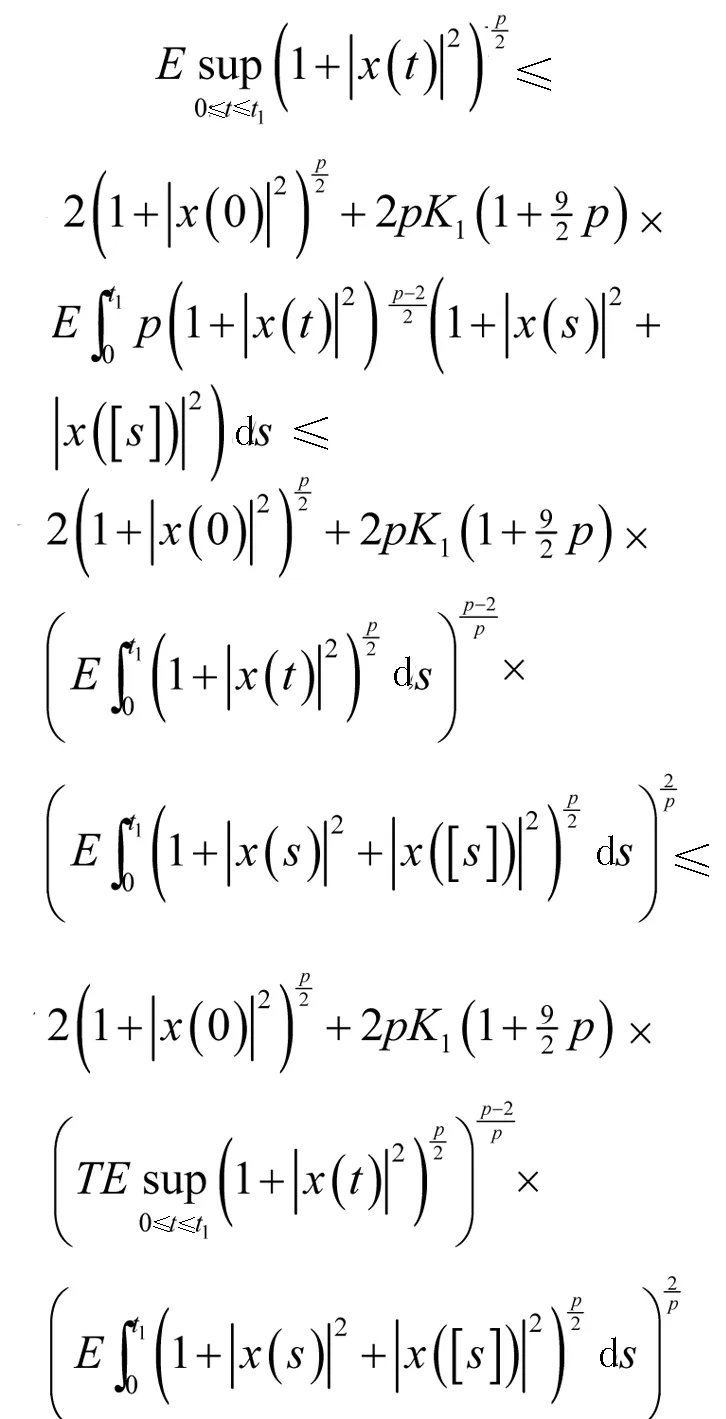
因此，能够得到

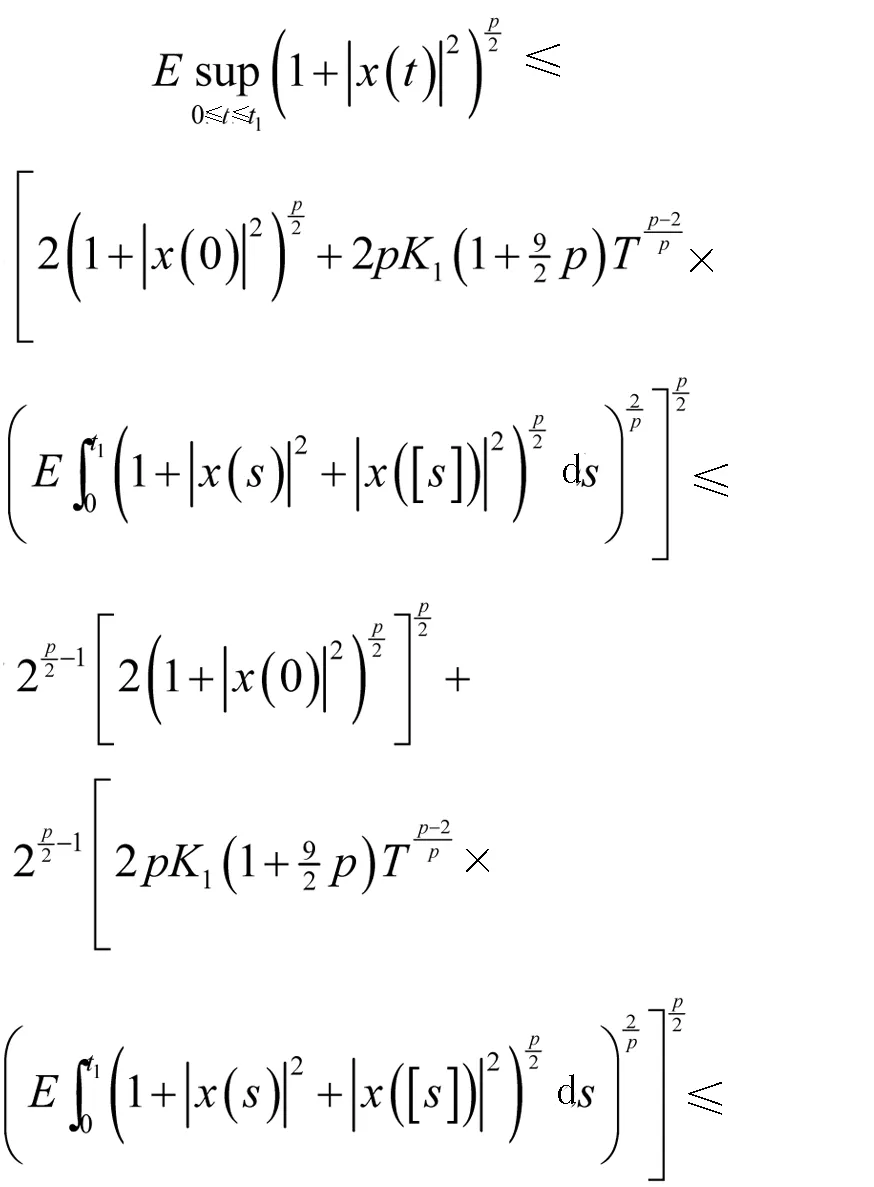
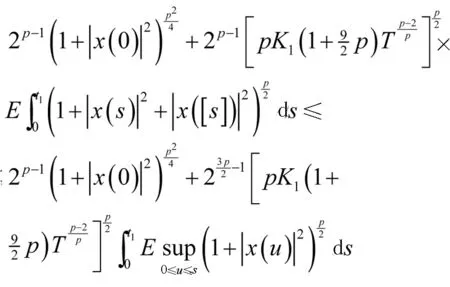
2.4 数值算例分析

证明方程dx(t)=(a1x(t)+a2x([t]))dt+(b1x(t)+b2x([t]))d(B)t,t≥0的数值解的收敛性.

解当a1=-2,a2=1,b1=0.3,b2=

0.1,x0=1时，利用E-M方法对方程进行求解，全局误差结果见表1.从表1可以看出这个数值算例的E-M方法是收敛的；在点T=2,3处的误差，通过计算得出它的误差值为E|ykm+l(ω)-x(T,ω)|2，这里的ykm+l(ω)是(8)在节点处的值.随后，估计在区间[0,5]上(ωi:1≤i≤1000)平均样本路径，即

由表1显示的数据可以看出在步长h=1/8时，T=2,3处的误差分别为1.155887107027968×