基于图像处理方法的大变形测量系统实验分析
2022-05-10刘占芳
王 昊,刘占芳
(重庆大学航空航天学院,重庆 400044)
0 引 言
大变形是一种常见现象,其复杂性使得人们无法应用以往测量小变形的方法对大变形应变场进行准确测量。近年来,随着越来越多的测量手段得到发展,利用非接触式测量方法,在大变形情况下应变的测量已不是问题,其中基于数字图像相关(DIC)的测量方法因其成本低,操作方便,测量精度高,可以测量全场位移等优点而被广泛关注及大量使用[1],其原理是通过对变形前后状态跟踪拍摄并进行相关计算来获得全场应变。然而由于小变形理论的局限性,现有的DIC方法通常并未对变形中的转动进行描述[2-4],根据连续介质力学理论,变形体内一点的运动包括平动变形和旋转变形,而一方面应变张量仅仅描述了平动变形,另一方面旋转矢量本身还不足以描述变形体内一点的旋转变形程度,为此需要引入曲率张量[5-6]。为描述大变形中的转动,本文受DIC方法的启发开发了一套大变形测量装置,并使用橡胶材料进行了平面拉伸实验,使用该系统测量橡胶材料,可以得到相应的变形数据,最终将这组数据应用到大变形分析中。
1 大变形描述
1.1 变形梯度及其分解
有限变形分析中的一个关键量是变形梯度F,它是描述变形和应变的中心[7],其张量表达的分量形式为:
FkK=xk,K
根据连续介质力学理论可知,对于有限变形,变形梯度可进一步分解成纯变形部分和纯旋转部分。从数学的角度来看,任一非奇异的张量F通过极分解可表示为正交张量R与对称正定张量U的乘积,或是对称正定张量V与正交张量R的乘积,分解的结果写成张量的分量形式如下:
FkK=RkMUMK=VkmRmK
其中第一个公式在连续介质力学中表示先作纯变形后作纯转动,第二个公式则反之;U与V的主轴相差一个转动。定义Cauchy-Green应变张量C为:
C=FT·F=UT·RT·R·U
其中,R是正交张量,即有RTR=I,于是右伸长张量U可以用C表示为:
U2=U·U=C
于是有:
左伸长张量V同理可求。一旦求出右伸长张量U,正交张量R可以由式R=FU-1求出。
1.2 应变张量
描述有限变形时使用的应变种类有很多种,包括Cauchy - Green应变张量、Euler - Almansi应变张量、Hencky应变(对数应变)等;在大变形情况下考虑选择对数应变作为应变的度量,对数应变不仅在理论上有其应用价值[8-10],目前有限元计算软件Abaqus在涉及超弹性材料的计算时使用的也是对数应变,因此本文不打算对对数应变的合理性进行阐述。当分解出左右伸长张量后,对二者取对数,得到两个应变张量:
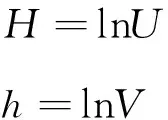
其中,H与h的特征值相同。
1.3 曲率
若要计算曲率首先要计算转角。计算出正交张量R后,对其取对数可以得到角张量A,进而可以得到转角α,其中角矢量α与角张量A的关系为:
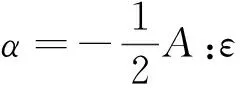
式中,ε为置换符号。曲率张量由此可得:
χkK=αk,K
2 橡胶拉伸变形测量实验设计
2.1 实验系统
模仿数字图像相关系统,本文设计并建立了一套单目视觉数字图像的大变形测量系统,包括测量装置以及计算软件。目前该系统可进行的实验类型仅包含单轴拉伸试验和纯剪切试验,通过该系统能够实现对试件的非接触式全场应变测量。整体设计图如图1所示,主要包括力学加载模块、数据采集模块和数据处理模块,其中力学加载模块和数据采集模块主要由卧式拉伸机、CCD相机、工业远心镜头以及若干燕尾式螺杆微调滑台组成,数据处理模块所涉及的软件需要自行开发。

图1 大变形测量系统硬件部分
2.2 试件选取
橡胶作为现实生活中随处可见的材料,同时具备几何非线性和材料非线性,作为本文研究非线性大变形问题的实验材料属实最佳,本文以硅橡胶作为实验材料。对试件进行平面拉伸实验,因此采用长方形试件,长宽比要大于 5∶1 才能保证试件中部为纯剪切受力[11],本文采用长宽比为10∶1,厚度为 2 mm。
2.3 试件制斑
数字图像相关方法的应用依赖试件表面的散斑,本次实验采用平板印刷法制取人工散斑,选择尺寸相同,布局呈网格状分布的均匀散斑,下文统称标志点作以区分,本文选择仅在试件的半侧制斑,标志点效果及拍摄所得图像的前五行如图2所示。

图2 试件的选择与标志点整体分布
2.4 实验过程
本实验使用行程加载进行控制,加载行程为15 mm,图3为橡胶加载示意图;之后调节镜头位置使成像最清晰。

图3 橡胶加载示意图
将试件离散化处理,标志点一一对应于各个离散的点,由于个中缘由本文中的标志点尺寸略有些大,实际越小越密集越好,当标志点足够小足够密集时,假设每一个标志点处的变形是线性的,因此每一点的变形梯度都是由常数组成;在试件
表面布好标志点后,通过图像方法识别出每个点的形心坐标,作为所对应的离散点的坐标;使用有限差分方法计算变形梯度,本文选择向前差分,只有在不能向前差分时选择向后差分,计算某一点的参数时还需要其相邻两个点的坐标值,三个点的分布如图4所示。

图4 标志点局部分布
将识别得到的坐标数据带入上述公式中,即可得到变形梯度、对数应变以及曲率等变形数据。
3 实验数据与分析
对试件施加载荷,并将变形前后的状态拍摄下来,如图5所示。

图5 简单剪切实验图像
适当处理图像,使之利于识别出感兴趣的部分,之后将图片导入编写好的程序中,计算变形梯度等参数;
计算得到的数据见表1,由于半场标志点数量过多,故本文只选取图2中所示的前五行数据进行展示。
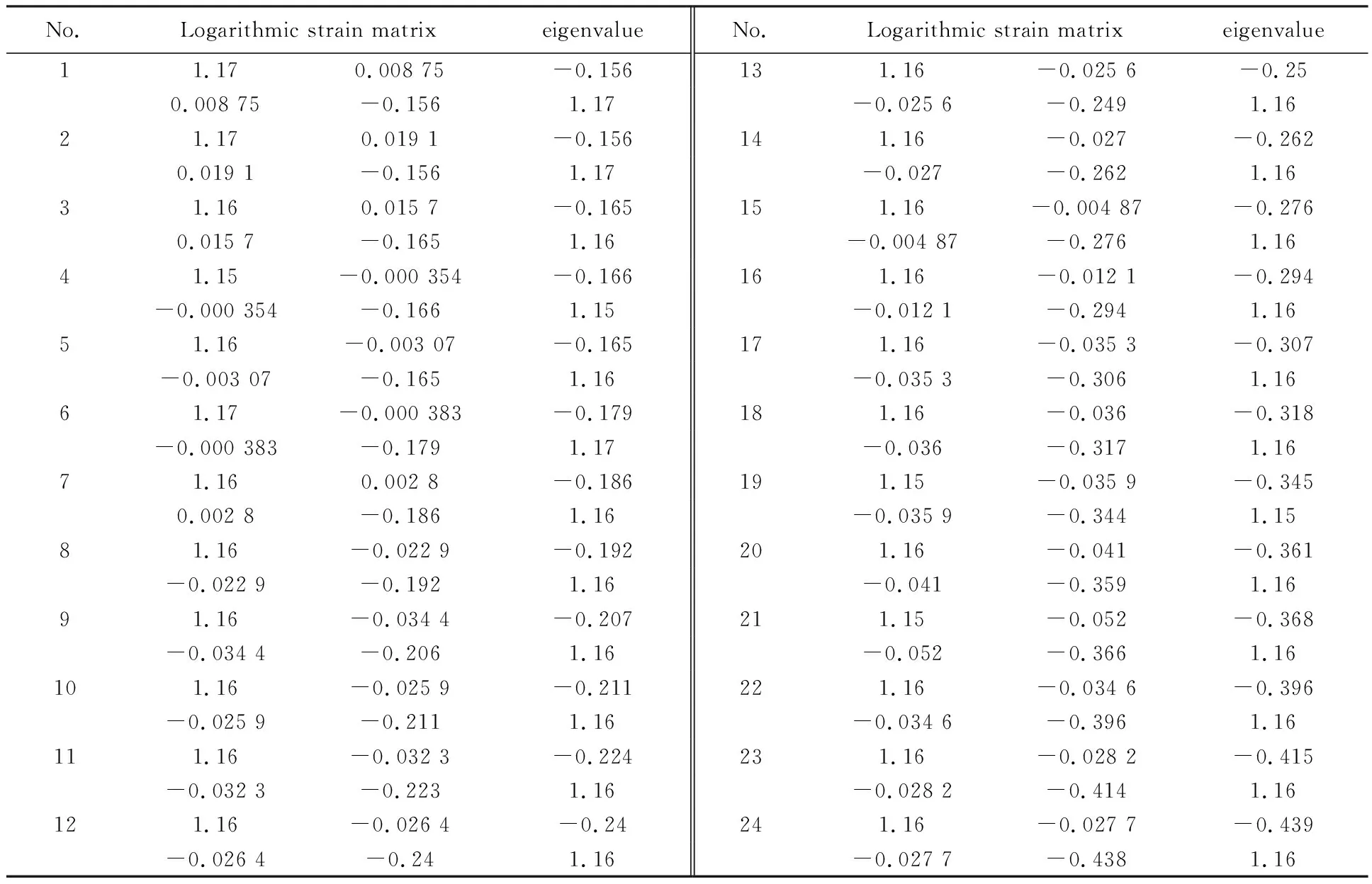
表2 应变数据
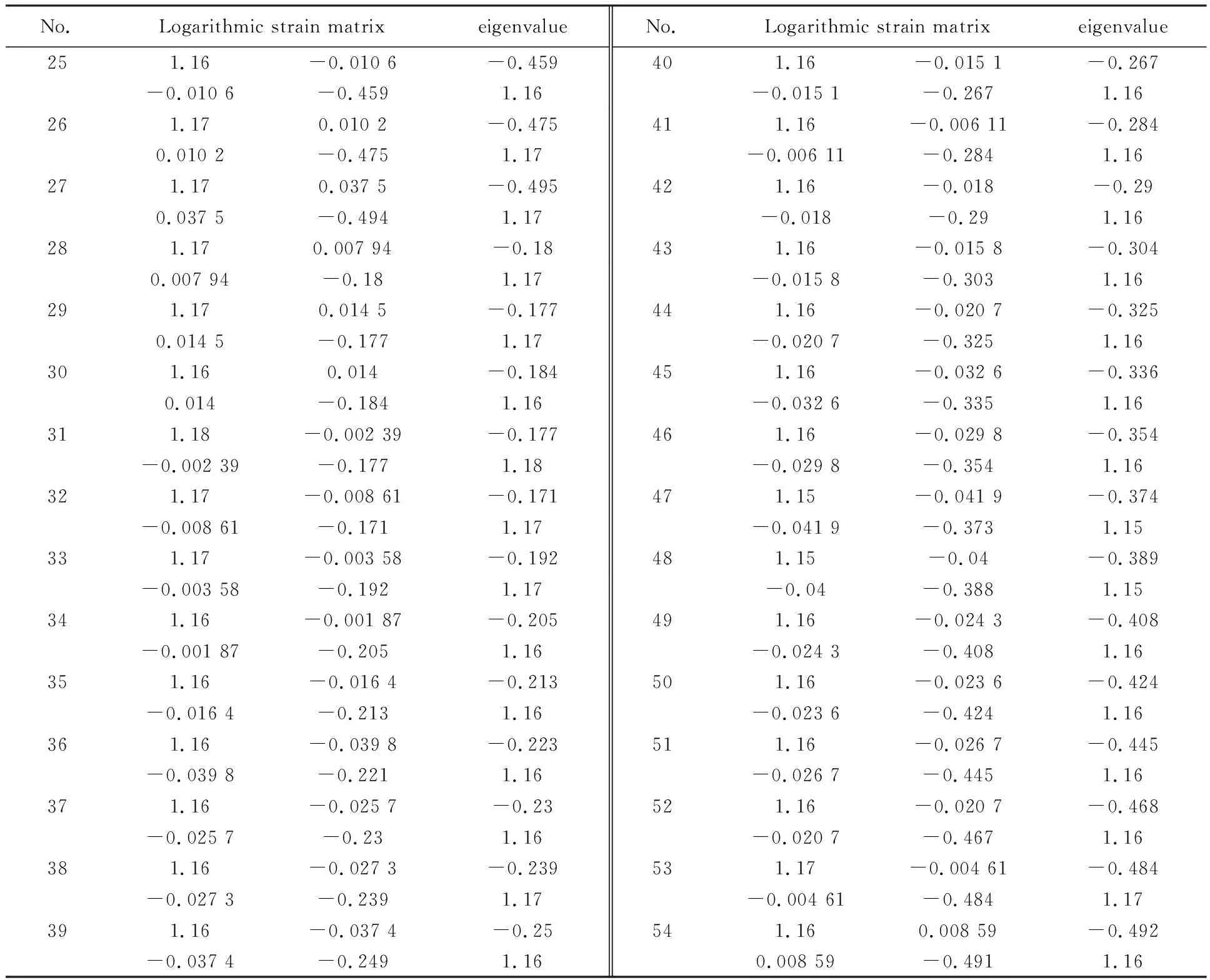
续表2

表3 转角数据
变形趋势图如6所示。

图6 半场变形趋势图
从图中可以看出半场内大致变形趋势,转角值的大小随纵坐标增加而增加,1/4场内随横坐标增加而增加;将转角的单位转换成角度制,并取其绝对值,对其进行插值处理,得到半场变形转角分布图如图7所示。

图7 半场转角云图(角度制)
由此可以得到转角分布规律,从图7中可以发现第一象限区域的转角值随着X、Y方向逐渐增大,且随着Y坐标值的增大,转角值增大的速度也随之增大;由于夹持不均匀等原因,试件左右两侧的转角值不完全相等,但大致趋势一致,观察第二象限区域可发现转角值最大约为8°,且在2/3处就已经减小了1/2。
4 结束语
本文开发了一套基于 CCD 图像处理的大变形测量系统,可以对发生大变形时产生的转动进行测量。此系统使用橡胶作为试件进行了平面拉伸实验,展示了变形梯度、对数应变以及转角的测量数据,并对转角数据进行插值处理,绘制出半场的对数应变云图及转角云图,从而进一步对橡胶等超弹性材料的大变形进行了描述,为预测大变形规律以及计算偶应力提供了支撑。
