数形结合思维与高中物理解题教学的融合
2022-05-10陈龙
陈 龙
(福建省福安市第一中学 福建 福安 355000)
引言
数形结合思想在高中物理解题中有着较高的应用率与较为广阔的应用面。教师在解题教学中,应加强对学生数形结合思维的培养,引导学生将几何图像与数理表达式结合在一起,对物理问题实施形象化、直观化、简化处理,将数理关系转变为图形,或将图形解析为简单的数理关系,把握物理问题的本质,快速找到正确的解题思路,实现高效解题。期望本文能够为广大物理教学工作者带来一定的参考作用。
1.高中物理与数形结合的关联
高中物理教学中,处处可见数形结合思想的影子。如师生对一系列物理现象的分析,通常需建立在物理模型之上,而图形与数字是表现物理模型的重要工具,这便体现了数形结合在物理课堂中的渗透。如教学“动能定理”习题时,教师会引导学生以作图、标点、标量的形式,表达状态变化过程、状态量与过程量,等等,尤其是在教学“动量守恒定律”时,教师会要求学生借助数形结合方式,表达矢量的大小及方向,这也体现了数与形的转化。总之,数形结合在高中物理课堂中的渗透既是广泛的,又是深刻的,为培养学生的物理素养、强化学生的物理解题能力,在教学过程中,教师应重视为学生渗透数形结合思想,为学生传授一些科学的数形转化方法,以促进学生学习能力的持续发展[1]。
2.数形结合思维在高中物理解题中的价值
2.1 数形结合可帮助学生实现高效解题。实践解题中,数形结合不失为一种行之有效的解题工具,学生可利用这一工具,完成高效解题。具体而言,相较于初中物理题目,高中物理题目的抽象性、严谨性与逻辑性陡增,很多学习基础尚可的学生,在解答一些抽象性强的问题时,都会频频出错。分析学生的解题现状可知,难以理清题干、分析清楚物理量、数量之间的关系,是阻碍学生实现高效解题的重要因素。而培养学生的数形结合思维,无疑能够帮助学生更好地解决如上问题。例如,学生可利用数形结合思想,以数形转换的方式,对一些抽象的物理量进行直观化、形象化处理,以更好地梳理题干,快速找到解答问题的正确思路,这与高中生本身的认知特点也是相符合的。
2.2 数形结合可增强学生的学习兴趣、学习信心。高中生的抽象思维尚在发育,形象、直观的事物,对他们而言仍然有着较强的亲近感,学习起来较为容易。因此在解题教学中,教师也可借助数形结合思想,激活学生的学习主动性,鼓励学生自主寻找物理解题点,让学生自觉感受到物理题目并非是晦涩难懂的,而是充满趣味的,进而帮助学生树立更为坚定的物理学习信心,这与课程改革倡导的“学生是课堂的主体,教师是课堂的组织者、参与者与引导者”的教育理念不谋而合[2]。久而久之,学生的物理思维也会得到长足的发展。
3.数形结合思维与高中物理解题教学的融合
教师可从如下四角度出发,理清数形结合思维与高中物理解题的关系,之后循序渐进地为学生渗透这种解题思想,潜移默化增强学生的解题能力:
3.1 把握数形结合与物理题的关联。为实现数形结合与高中物理解题的深度融合,教师应当理清数形结合与高中物理解题之间的关系,即数形结合在物理题中的具体体现,以有的放矢地培养学生的数形结合思维。这要求教师在平时吃透教材,加强习题归纳,形成系统性的解题教学思路,为解题教学的顺利进行打下良好的铺垫[3]。以高一物理为例,学生在解题过程中,对数形结合思维的运用集中于如下三种图:
(1)速度时间图像(v-t图)。
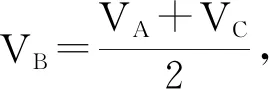
解析:本题条件过少,采用公式进行解决难度过大,且耗费时间过长,因此在考场上不建议学生如此解题。但条件过少的物理题目,往往暗示着我们可以借助数形结合思想,以画图的方式解决。如图1,可借用中间时刻速度与初末速度的关系,学生在画图时,通常会画出匀变速直线运动的图像,将线条画至C点,但题目给出B点是位移中点,为保证前后位移一致,图线只能移至A点,则可判断a1及a2的大小关系是a1 图1 (2)矢量图。 【例2】小船在静水中速度为u,水速为v,且v>u,若需以最短航线渡过宽度为L的河流,应如何行驶?求最短航线长。 解析:题目给出了v>u的条件,未给出小船的速度方向,学生在解题时,可使用数学中的圆工具和矢量合成的三角形法则,以v右端点为圆心,u的大小为半径画出半圆图,航线最短时,小船合速度应尽可能靠拢垂直于岸的方向,如图2所示,v合与u垂直时,小船航线最短,cosɑ=u/v,船身应以偏向上游ɑ=arccos(u/v)行驶,最短航线长度为smin=L/cosθ=L/cosɑ=vL/u。 (3)运动示意图。 在实践教学中不难发现,在解答物理习题特别是追逐类问题时,学生绘出运动示意图后,往往能够较为清晰地察觉物体间的位移关系,即线段长度的关系,解题难度迅速降低,结合运动图像,可实现高效解题。 在实践教学的解题过程中,常遇到的可以用数形结合思想进行解题的题目,或绘制的图像的类型做出归纳,在课堂中,引导学生初步构建起以数形结合解决物理问题的系统化框架,之后再循序渐进地培养学生对以数转形、以形转数、数形互补三种具体解题方法的了解。 3.2 渗透“以数转形”思想,简化物理题目。学生在解答物理题目时,面对题目中给出的复杂的代数量,往往会产生迷茫的心态,找不到解题的正确切入点[4]。此时物理教师便可不失时机地引导学生转变自己的思维,从数形结合的角度出发,利用形象、直观的图形,梳理题目中的代数关系,简化题目,以实现高效解题。这种“以数转形”的解题方式,也是数形结合思想应用于高中物理解题的最为基础的形式。 【例3】百米赛跑中,计时员听到枪响后,开始记录运动员的跑步成绩。当计时员看到第一个运动员到达终点后,暂停秒表,得出该运动员的赛跑成绩是12.2s。请问,这种计时方法合理吗?若不合理,应如何计时才能够保证计时结果的准确性? 解析:依据图中信息,我们简单地绘出图形,用AB代表两名运动员的百米赛跑跑道,A为起点,B为终点,持枪者与运动员一同站在A点位置,计时员站在B点位置,忽略运动员的反应时间,可将枪响与运动员起跑视作在同一时间点上发生的行为,但枪声传至B点,还需经历一段的时间,运动员已在这段时间内跑了一定的距离,从这一角度上来看,题目所述的计时方法是不合理的。学生结合生活经验不难判断出,合理的计时方法是看到枪响冒出的烟开始计时,即现实中百米跑比赛最常用的计时方法,这一方法主要借助了光的传播原理,即光在空气中的传播速度比声音快。 3.3 渗透“以形转数”思想,归纳数据关系。实际解题中,有的物理题是带有图像的,包括运动状态图、实物图等,但题目却并未给出详细的数据信息,此时,学生就应仔细观察题目,归纳数据关系之后做出正确的计算,这便是“以形转数”。 【例4】一个半径R=0.8m的1/4光滑圆弧轨道固定在竖直平面内,其下端切线是水平的,轨道下端离地h=1.25m。现有质量m=0.1kg的小物块A由轨道顶点从静止开始释放,落至B点,忽略空气阻力,其重力加速度g取10m/s2,求A落至轨道下端时的速度大小。 3.4 渗透“数形互补”思想,培养综合思维。分析学生常做的高中物理习题可知,很多物理习题有着较强的综合性,在应用数形结合思维进行解题时,学生需综合考虑数、形之间的关系,以“数形互补”思想,找到正确的解题思路[5]。因此实践教学中,教师也应加强对学生综合思维的培养,让学生能够从更宽广的视角出发,思考物理习题,结合题目给出的条件,理清图形、数量之间的关系。 【例5】现有一长木板运动于水平面上,t=0时,放置一个静止物体至木板上方,之后长木板运动时间与运动速度之间的关系如图2所示。若静止物体的质量与长木板质量相等,同时水平面、长木板、静止物体之间皆有摩擦力,静止物体与长木板的最大静摩擦力与滑动摩擦力相等,整个运动期间,该物体都保持在长木板上,求长木板与物体及长木板与水平面的动摩擦因数。 图2 解析:解答此题时,学生需先分析小物块与长木板的受力,进而判断其运动情况。0s至0.5s阶段,长木板与物体间、长木板与地面间皆有摩擦力,小物块做匀加速运动,长木板做匀减速运动,直至0.5s,二者速度相等。该阶段可用加速度定义式算出小物块加速度大小,再结合牛顿第二定律,求出小物块与长木板之间的动摩擦因数,计算图中0s至0.5s图像斜率可得出长木板加速度,再以牛顿第二定律计算长木板与水平面之间的动摩擦因数。在进行对这道题的解题教学时,教师应重视引导学生绘制受力分析图,判断物体运动情况,找到正确的解题思路,之后利用方程求出答案。 4.1 概念教学入手,渗透数形思维。以对“力学”相关知识内容的教学为例。在讲解新内容时,教师可为学生举“足球”这一实例:球员在罚点球时,足球由静止状态转为运动状态,守门员接住球时,足球又从运动状态转回静止状态。教师可引导学生以画图方式,分析这一例子,探究物体状态为何而改变。当学生察觉到,是力的作用引发了物体运动状态的改变时,教师就可为学生引入力的示意图,以带箭头的有向线段表示力,让力的概念变得直观而具体,并以线段长度表示力的大小。显然,相较于常规教学方式,上述画图教学方式,更有利于帮助学生全面理解物理概念、形成初步的数形结合思维。再如,在教学电场、磁场时,教师也可在黑板上绘出电场线、磁场线,以表达物理概念,让学生形成在学习物理知识、解答物理问题时画图的习惯。 4.2 鼓励自主探究,培养数形思维。在教学过程中,对于一些难度不高的知识内容,教师可将课堂自主权交由学生,引导学生以数形结合思维进行探究,以深化学生对这一思想方法的了解,长此以往,学生必然能够将数形结合思想熟练地应用到物理解题中,物理素养也能够获得长足的发展。 以对“力的合成”相关知识内容的教学为例。教师可为学生引出如下情境:现有一根橡皮筋,原长5cm,重力忽略不计,上端固定。利用弹簧测力计拉伸橡皮筋至15cm,之后再测一次,用两个弹簧测力计,将橡皮筋拉伸至同一位置,两个弹簧测力计成一定角度。教师可引导学生结合这一案例,绘制示意图,分析得出F单独作用与F1、F2共同作用的效果是相同的。在此基础上,教师就可为学生直观地引出合力、分力、等效替代等概念了。 4.3 结合生活情境,培养应用能力。物理知识来源于实际生活、回归于实际生活、服务于实际生活,进行物理教学的主要目的是培养学生以物理知识,解决生活中的实际问题的能力。因此,当学生对数形结合思想有了充足的了解后,教师应鼓励学生以数形结合思想,构建生活化的问题情境;反之,在形成一定的物理素养后,学生在实际生活中,也可借助数形结合思想,将真实的场景转化为物理问题,之后深入分析物理问题,找到正确的解题思路。这便是所谓的“物理抽象”,是学生将生活经验与学习经验结合在一起的过程。 综上所述,在现阶段的高中物理解题教学中,数形结合思想有着较高的应用率与较为广阔的应用面。在日常教学中,教师应坚持为学生渗透数形结合思想,引导学生利用这一思想,更好地判断物理题隐藏的数理条件,高效地找到正确的解题思路。同时,教师在平时也应引导学生做好对物理习题的归纳总结,分析解题规律,形成数形结合思维,以更为得心应手地解决物理问题。长此以往,学生的物理学科核心素养必将得到突飞猛进的成长。
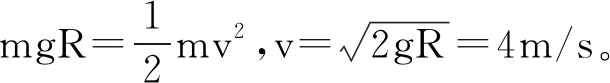

4.如何培养学生的数形结合思维
结语
