基于四旋翼无人机的运动目标跟踪控制研究*
2022-05-10陈旋
陈 旋
(江苏科技大学电子信息学院 镇江 212000)
1 引言
近年来,四旋翼无人机越来越受到工业界和学术界的关注。它具有垂直起降、低成本制造等特点,可广泛应用于空战中敌方目标跟踪锁定、及时发现并锁定海上搜救中的遇难者等任务[1~3]。运动目标跟踪技术是四旋翼无人机完成这些任务的关键技术,逐渐成为研究领域的热点问题。在运动目标跟踪系统中,无人机的目标跟踪分为姿态跟踪和位置跟踪两部分[4]。在姿态跟踪方面,无人机具有非线性、强耦合等特点,给控制器的设计增加了难度。目前,许多研究者采用滑模控制[5~6]、自适应控制[7]和神经网络控制[8]等方法来实现控制器设计。在位置控制方面,四旋翼具有6个自由度和4个控制输入,控制律设计过程复杂,同时,无人机还需要保持一定的距离来跟踪目标。因此,位置控制器的设计比姿态控制器更具挑战性。文献[9]提出了一个由无人机和另一个飞行器组成的系统,无人机可以固定距离跟踪目标。文献[10]利用人工势场(APF)构造了避障时间、避障能量消耗等函数,使无人机能够高效、经济地避障。文献[11]用滑模控制方法研究了四旋翼系统的跟踪控制设计。该方法在系统受到干扰时,能可靠地跟踪目标的期望轨迹。
本文受上述文献的启发。首先,提出了一种由位置环和姿态环组成的双环控制系统,来实现四旋翼的高精度目标跟踪;其次,提出了一种人工势场,使无人机能够在一定距离内跟踪运动目标,同时,为了提高无人机的抗干扰能力和跟踪性能,提出了一种滑模控制器;最后,为了保证姿态跟踪的快速收敛和高精度,提出了一种由滑模控制和RBF神经网络算法组成的姿态控制器。
2 数学模型
无人机是跟踪运动目标过程中最重要的被控对象。四旋翼无人机的简化结构如图1所示。
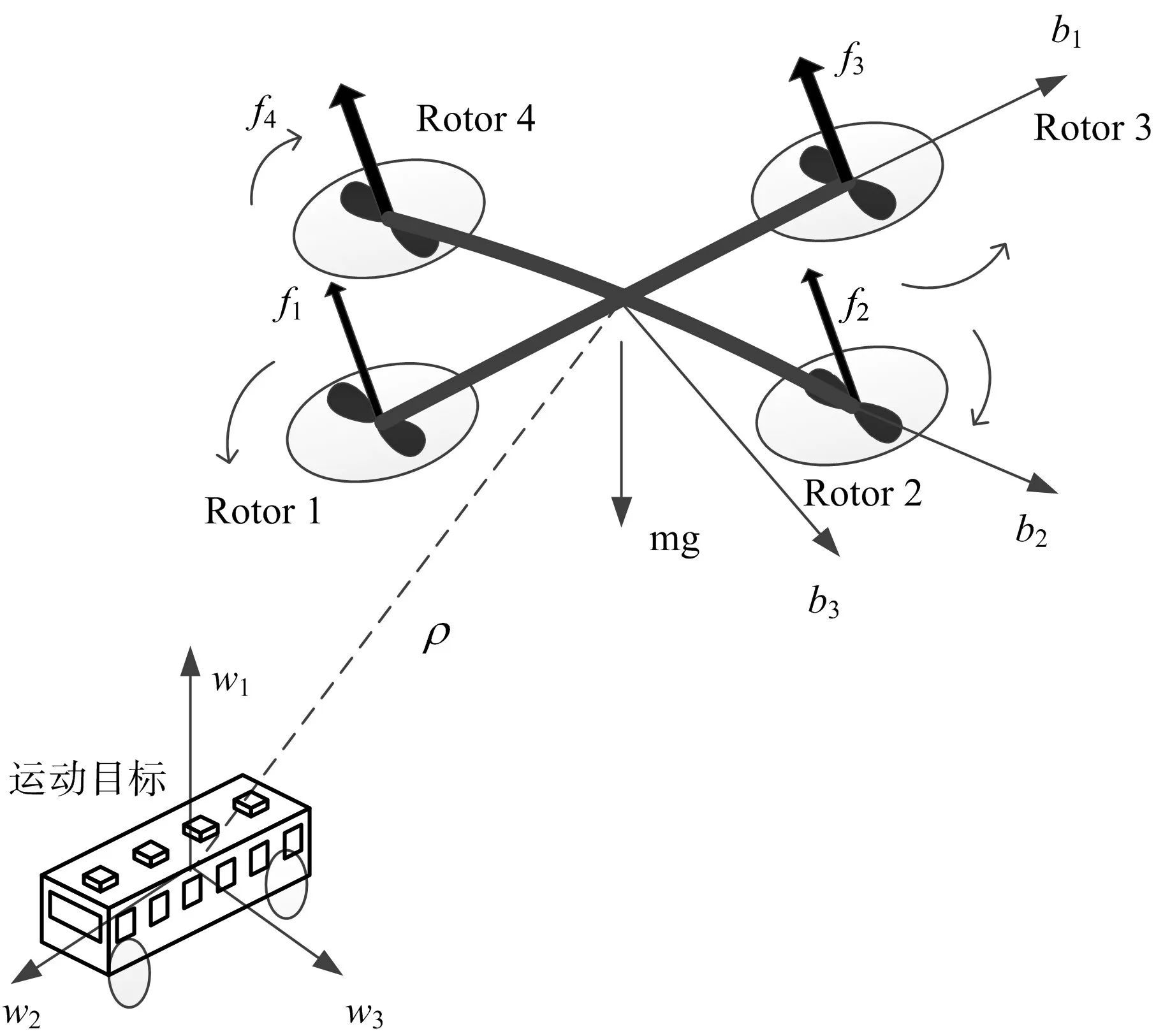
图1 目标跟踪系统模型图
其中,{w1,w2,w3}和{b1,b2,b3}分别表示大地坐标系和体坐标系,f表示总升力。根据牛顿-拉格朗日建模原理,将系统动力学模型建立为方程(1)和方程(2)[12]。
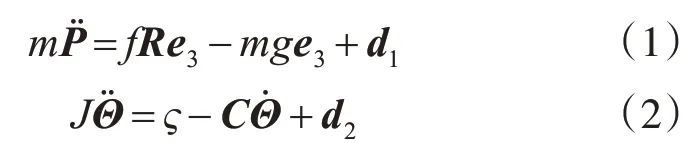
其中m是总质量,P=[xyz]T是四旋翼质量中心在惯性坐标系中的位置。Θ=[φθψ]T为欧拉姿态角,g为重力加速度,e3=[0 0 1]T为垂直方向的单位矢量。f和ς=[ςφςθςψ]T为系统的控制输入,分别表示姿态系统的升力和转动力矩。d1,d2表示对无人机的干扰力和气流力矩。R表示从刚体坐标系到惯性坐标系的平动速度变换。J是惯性张量I=[IxxIyyIzz]T在惯性坐标系中的表示。其计算公式如下:
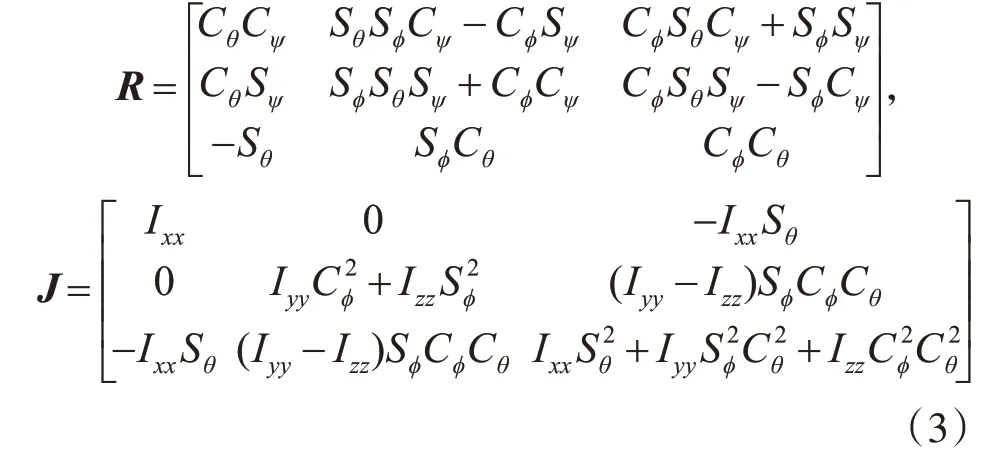
其中C(·)和S(·)分别表示余弦函数和正弦函数。C表示科里奥利及离心力项,可通过以下公式计算[13]:
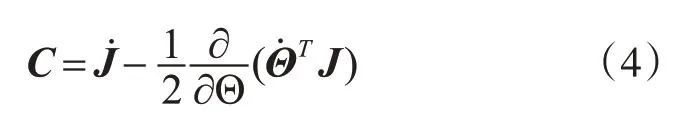
从无人机到目标质心的距离可以定义为ρ=P-Pt,Pt表示运动目标的位置。无人机通过保持一定距离跟踪运动目标来实现目标跟踪,ρd是期望的跟踪距离,然后eP=ρ-ρd可以定义为相对距离的跟踪误差。
3 控制器设计
整个控制系统是由内外环组成的控制系统结构如图2所示。位置系统为外环,姿态系统为内环。外环产生两个中间命令信号θd和φd,并发送到内环系统。内环通过控制律跟踪两个中间指令信号。

图2 四旋翼闭环控制系统结构
3.1 位置控制器设计
由式(2)可以得到位置系统的误差方程。
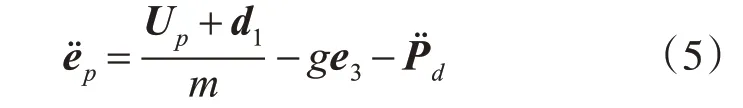
其中Up=f Re3是要设计的虚拟控制输入。分别设计了四旋翼与目标之间势场的斥力和引力。首先,斥力势被构造成广义Morse函数[14]。

其中k是一个正常数。如果平衡点人工势场的速度场为0,参数k、b、c应满足:
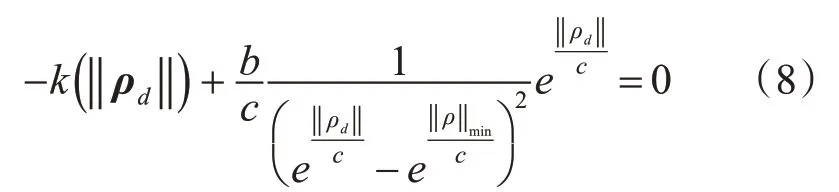
‖ρd‖=‖ρ‖时达到平衡态,当‖ρ‖min<‖ρ‖<‖ρd‖时,斥力在小范围内起主要作用;当‖ρd‖<‖ρ‖≤‖ρ‖min,引力势在大相对距离内起主要作用;当‖ρ‖>‖ρ‖max,人工势场不再工作。
在给出无人机与目标之间的人工势场后,需要定义无人机与目标之间的相关速度场,以实现稳定跟踪。将斥力势与引力势相结合,可以得到飞行器与目标之间的速度场函数。

定理1:考虑了式(1)中所描述的四旋翼动力学,如果根据式(10)和式(11)设计滑模控制器和控制输入,则控制状态可以保证位置跟踪误差收敛到零。

设计如下自适应律:

3.2 姿态控制器设计
姿态控制器为内环控制器,将RBF神经网络与滑模控制相结合运用到四旋翼无人机的姿态控制,其目的是保证姿态位置{φ,θ,ψ}收敛到有界的期望轨迹{φd,θd,ψd}。该模型的状态空间形式可由式(3)写成:

抖振是滑模控制中不可避免的问题,可以用神经网络进行补偿。同时,在实际工程中,很难得到准确的f(·)和g(·),RBF神经网络算法可以有效地解决这一问题。假设f(·)和g(·)是两个未知的非线性函数,分别使用两个RBF神经网络函数来逼近f(·)和g(·)。神经网络的算法如下:

定理2:考虑了式(2)中所描述的四旋翼姿态角动力学,如果根据式(16)和式(20)设计滑模控制器和控制输入,则控制状态可以保证姿态跟踪误差收敛到零。


4 仿真与分析
为了验证本文所提出的控制方法的有效性和有效性,包括针对位置和姿态跟踪问题所获得的性能,本文对所提出的控制方法进行了仿真验证。此外,还选择了一种基于二阶滑模控制器(2-SMC)[15]的综合控制器进行比较,以显示该策略的改进效果。假设目标为小车,运动方向不断变化,四旋翼的初始位置和姿态角值为[0,0,1.5]m和[0.2,0.2,0.6]rad,惯性矩阵I=diag(0.004,0.004.0.008),偏航角ψd=π/3。
位置控制器参数选择为‖ρ‖min=1,‖ρd‖=2,‖ρ‖max=5,k=10,b=16.83,c=2,a=1,λ1=λ3=1,λ2=3。姿态控制器参数调整为bj=5,γ1=10,γ2=1,λ4=5,η=0.5,cj=[-1,-0.5,0,0.5,1]。
2-SMC控制器的参数如下ms=1.1,l=0.21,lx=ly=1.22,lz=2.2,lr=0.2,Ki=0.1(i=1,2,3),Kj=0.12(j=4,5,6),b=5,k=2,C=1。假设两个慢时变扰动是无人机的气动力和力矩,它们的大小可以近似为
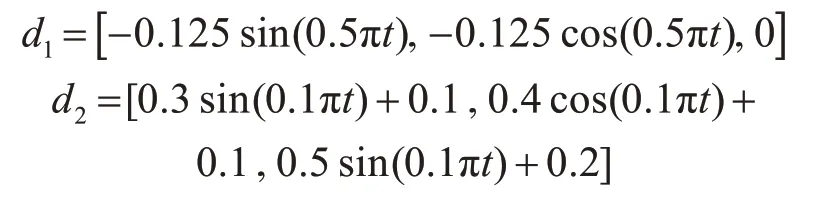
假设目标沿着螺旋上升的轨道运动,目标的运动轨迹近似地描述为
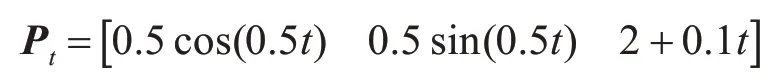
仿真结果如图3~5所示。由仿真图3可知,运动目标跟踪控制系统能满足飞机的跟踪性能要求,APF&RBF由于收敛速度快,跟踪效果也优于2-SMC。图4表明,APF&RBF的位置跟踪比2-SMC的位置跟踪具有更好的收敛性能。图5显示了姿态子系统对三个姿态角的跟踪效果。在RBF中,俯仰角和滚转的最大波动误差小于0.1弧度,由于偏航角的期望值是恒定的,因此几乎没有波动误差。与2-SMC相比,RBF算法的三个姿态角能够更快地跟踪指定的姿态角,具有更好的稳定性。
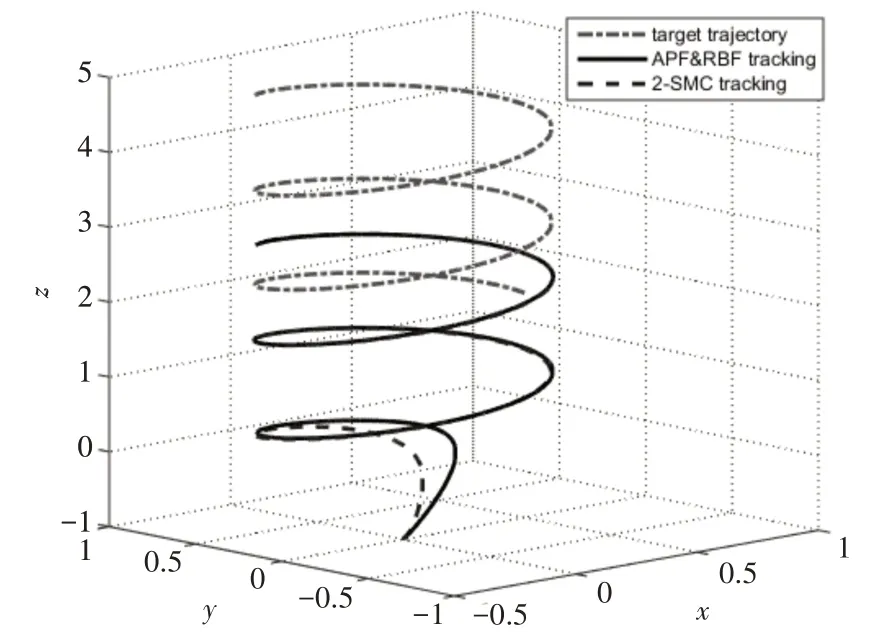
图3 目标跟踪三维效果图
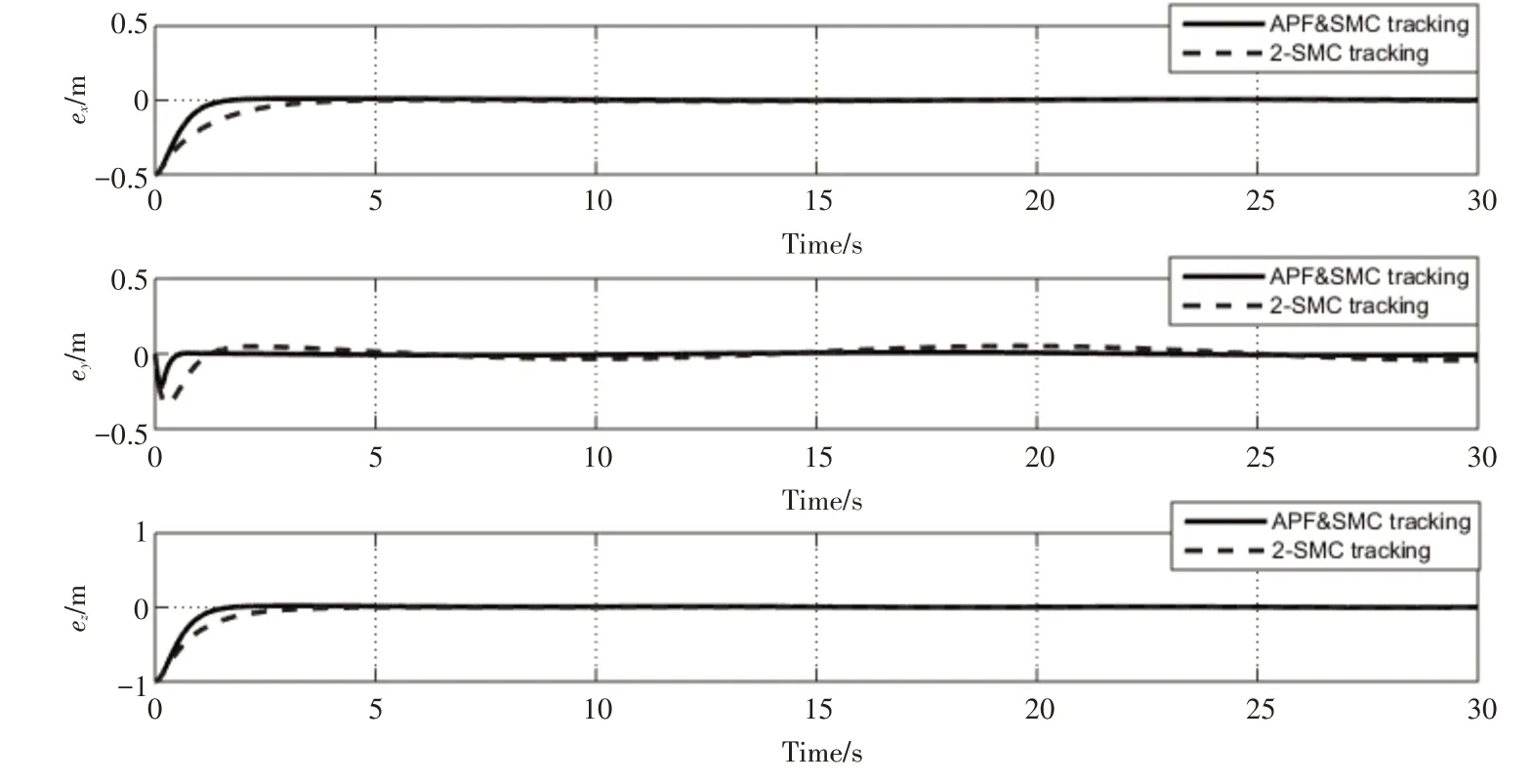
图4 位置跟踪误差
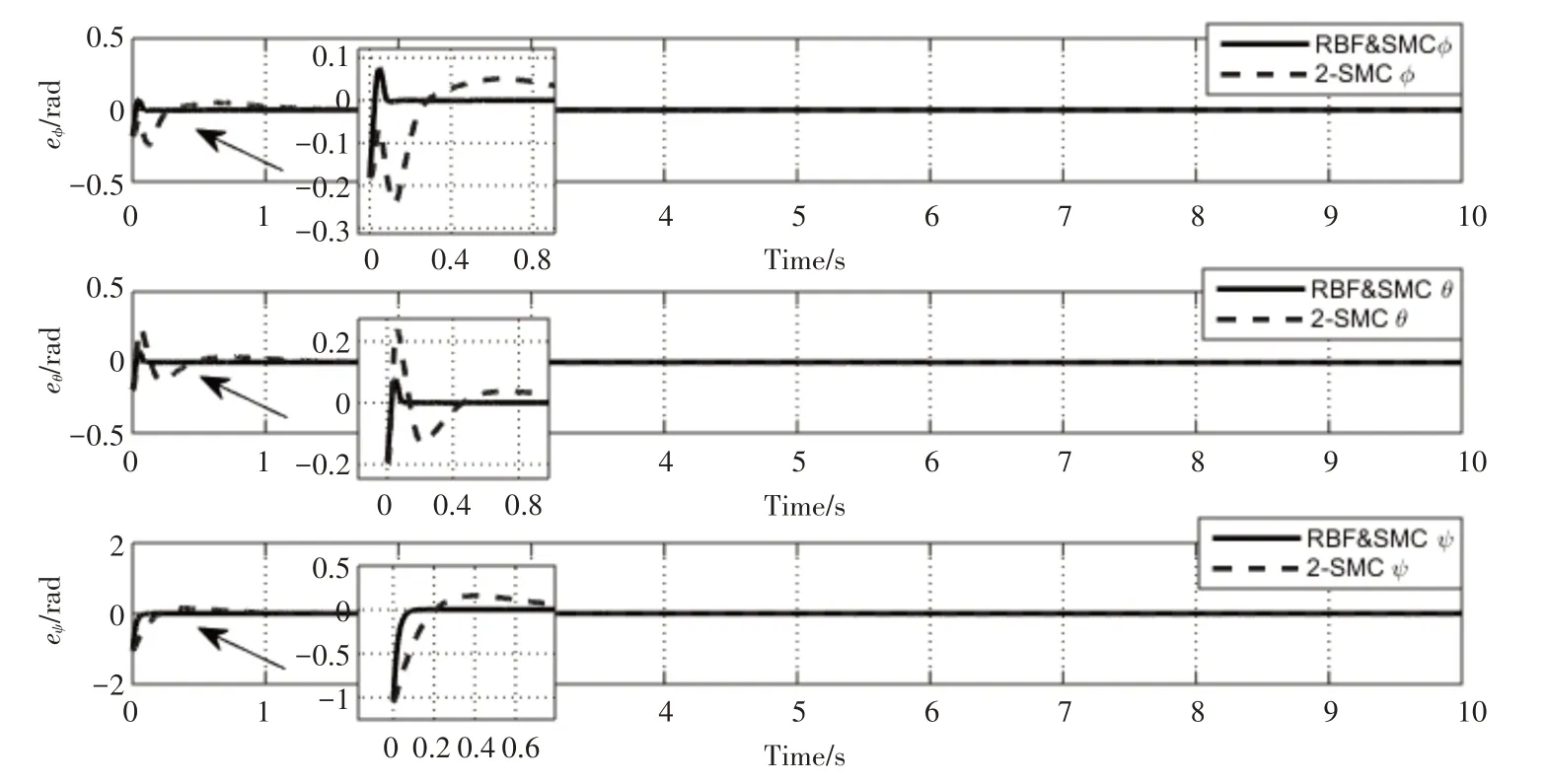
图5 姿态角度跟踪误差
5 结语
本文提出了一种高精度的运动目标跟踪控制算法。控制结构由位置控制器和姿态控制器组成。在位置控制方面,设计了同时发射斥力和重力的人工势场理论,实现了在一定距离内对运动目标的稳定跟踪。为了使姿态子系统快速跟踪中间指令信号,克服外部气动干扰力矩和惯性矩阵的不确定性,提出了RBF神经网络与滑模控制结合的控制器。仿真结果表明,该控制系统在运动目标跟踪情况下具有良好的鲁棒性和跟踪性能,可应用于类似的运动控制系统。
