基于信噪比的KPCA-SVM-KNN算法的股价预测研究*
2022-05-10王冰玉刘勇军
王冰玉 刘勇军
(华南理工大学工商管理学院 广州 510640)
1 引言
股价预测是投资策略形成和风险管理模型发展的基础[1]。一个准确的股价预测可以为投资者提供更多在证券交易所获利的机会,但由于股价趋势的波动性、不规则性和高度不确定性,股价预测一直是极具挑战的问题[2~3]。
目前,在股价预测方面,相关学者已提出许多用于指标构建和股价预测的计算模型和智能算法。在实践中,Panigrahi等[4]借助16个数据集的时序股价数据,提出ETS-ANN模型预测股价。Huang等[5]将情感分数整合到逻辑回归模型,使用网络意见来提高股票价格预测的性能。Oztekin等[6]将开盘价、收盘价、收盘汇率和FBIST债券指数等历史数据作为输入变量基于SVM进行股价预测。Nayak等[7]考虑简单移动平均、指数移动平均和AR等技术指标作为指标变量构建SVM-KNN模型预测股价。王淑燕等[8]以市销率、市净率、市盈率、股票收益率等16个指标作为输入变量,借助随机森林进行量化选股。在理论上,Chen等[9]对Nayak的思想进行创新,把特征加权向量纳入并试验,最终提出加权SVM和加权KNN的股价预测方法。杨善林等[10]将误差校正方法引入,构建改进的GARCH模型预测股价趋势。张贵生等[11]将滞后点的变化趋势信息纳入,提出基于微分信息的ARIMAGARCH股价预测模型。
针对当前研究,不难发现,现有的股价预测模型只考虑股价中所含的历史和趋势信息:股票价格、财务指标和技术指标,未曾考虑噪声信息对预测结果的影响,这在一定程度上影响模型分析时序数据的泛化能力,导致对股价趋势变化方向的错误判断,进而影响股价预测准确性[12]。现有文献已表明使用噪声处理的数据进行预测,会获得一个更好的预测结果[13~15]。为降低股价趋势所含的噪声信息和输入变量之间的相关性对股价预测结果的影响,本研究构建信噪比特征向量,并采用KPCA算法对输入变量降维处理,之后借助Nayak[7]的SVM-KNN算法进行股价预测。
2 研究方法
2.1 核主成分分析(KPCA)
KPCA是对PCA的扩展,考虑将原有数据投射到高维特征空间,在此空间中实现PCA操作的新型非线性降维方式[16]。对于输入矩阵X=[x1,x2,…,xN]∈Rn×d,其中,xi为在时间i内的股票相关数据样本,N表示样本总量,d表示数据总维度。本文采用如下方式的非线性映射函数φ(·)实作为从数据空间到特征空间的映射:

φ(xi)为向量xi在特征空间中的表示,且φ(xi)满足以下条件:

之后,通过以下方式定义协方差矩阵:

其中,φ(xi)的均值为零。此外,因为φ(xi)不可直接获取,故经过对空间中特征值分解的方式获得:
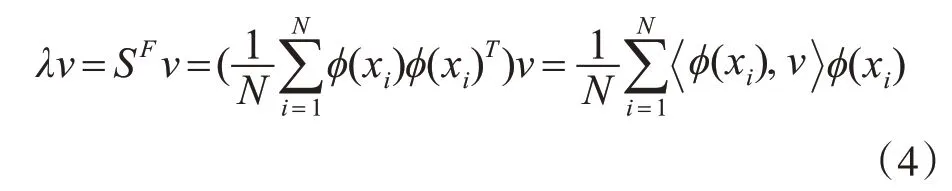
其中,λ和v为SF的特征值和特征向量,为内积。在λ≠0的情况下,所有的特征向量v都在此空间的训练数据范围内,并且,存在系数αi∈{1,2,…,N}使下式成立:

连接式(4)和(5),两边同乘φ(xk),可得到:
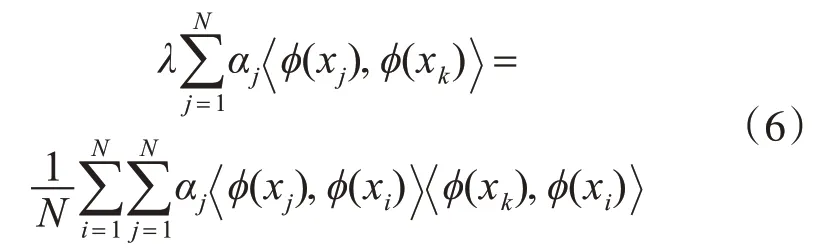
从式(6)发现:如果得到非线性空间中的内积就可有效处理协方差矩阵中所面临的分解问题。本文将由N×N代表的核矩阵K定义为

由上可知,我们可引入式(7)得到内积。目前,核函数主要有多项式、线性和径向基核函数三种[9]。因为股价趋势变化具有高度不确定性和非线性,本文选择径向基核函数作为KPCA算法的核函数。其形式为
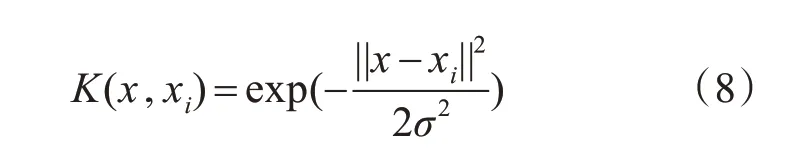
其中,σ为常数。当式(2)不成立时,需将式(8)调整为

其中,I1为N×N的单位矩阵,根据式(9),我们可将式(6)变为

λ值决定核主成分(PC)的选择,与较大λ值所对应的PC应保存在PC空间中。本文以将特征空间中的训练数据φ(x)映射到特征向量j的方式计算第j个提取的PC:

其中,k是PC空间中提取的主成分数量。
本文选取的累计贡献率p=90%。如果通过计算得到的某个特征值的累计贡献率≥90%,则提取该主成分。
2.2 SVM算法
SVM由Vapnik[17]最初提出的一种分类算法,其关键步骤:最初将向量映射到一个更高维的空间,在此空间建立一个最大间隔超平面;其次在超平面两边构建两个相互平行的超平面;最终构造两个距离最大化的分隔超平面,该平面与超平面平行。设包含N个训练样本的训练集样本对{(x1,y1),(x2,y2),…,(xN,yN)},其中xi∈Rd表示第i个训练样本的输入向量,d表示样本总维度,输出值由yi∈{+1,-1}表示。SVM主要解决以下优化问题:
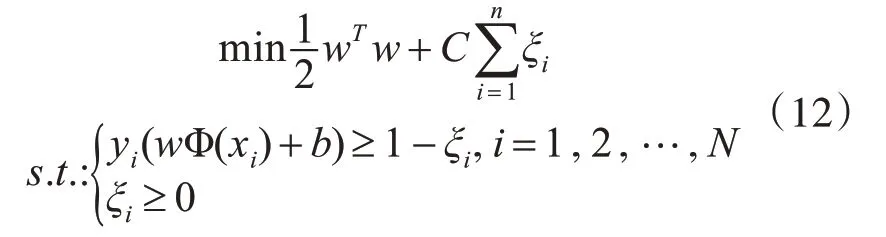
其中,C>0为修正项的惩罚参数,ξi为松弛变量,Φ(x)为非线性映射函数。wT为特征空间维数,b为待定的标量参数。
该算法中w的值可由拉格朗日对偶算法求出,其中为拉格朗日因子。本文采用核函数K(xi,xj)代替Φ(xi)TΦ(xj),通过求解得到最终的决策函数为

由于股票数据之间存在非线性关系,故文章选用径向基核函数作为SVM算法的核函数[6],即:
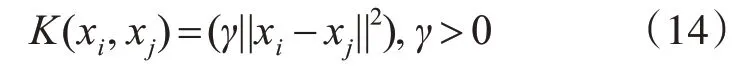
其中,γ是根据数据集初始化的内核参数,最佳核参数的选择受训练集大小的影响[7]。
2.3 KNN算法
KNN是一种非参数学习算法。与现有基于模型的智能算法不同,KNN需要将所有训练示例保留在内存中,以便搜索所有K个最近的邻居用于测试样品[7]。由于对不相关特征变量的间接敏感性,所以该算法对距离函数比较敏感。对于样本{(x1,v1),(x2,v2),…,(xn,vn)},其中,xi∈Rd是第i个训练样本的输入向量,d为样本维度,vi为输出值,用下式表示:

其中,xl为xi的最近邻。KNN以识别k个与测试数据具有最高相似性的加权最近邻作为决策准则。因此,KNN需要一个矩阵来测量测试数据与训练样本之间的距离。本研究采用当前使用较为广泛的欧式距离函数:
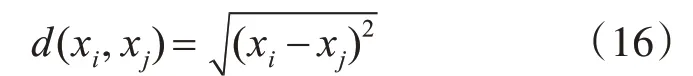
从而,股价预测用下式表示:

其中,P′为预测股价,Plast为前一天样本收盘价,vˉ为k个最近邻样本输出值v1,v2,…,vk的均值。
本文考虑到输入变量之间的相关性对预测结果的影响,在现有的SVM-KNN算法的基础上,构建新的KPCA-SVM-KNN算法进行股价预测。下面给出该算法的算法框架:

图1 KPCA-SVM-KNN算法的算法框架
3 股票指标的选取
股票市场中,输入指标经常以价格相关的历史数据的形式展现,如开盘价、收盘价、最低价、最高价和总交易量。目前学者通过研究发现加入一些相关的技术指标可以获得更有效的股价预测[9]。故为了更好的反映股价的波动,本文选取相关技术指标,且令xi为股票i的第i个输入样本,则有xi=(xi1,xi2,…,xi17)。本文所使用的指标及计算公式如表1所示。

表1 股价预测所需要的输入指标
其中,xi16表示判断SVM分类准确率的标准,用下式表示:

考虑到买卖的不稳定性,价格变化的非连续性、交易规模的巨大差异化和订单流的战略组成部分所包含的复杂性等因素的存在,导致我们所观测到的价格变化过程是一个包含噪声的过程[12]。实际上,我们一般所观测的对数形式的股价过程由对数有效价格和对数噪声两部分组成,其股价的对数形式为

其中,pi为股票第i个输入样本价格,x′i为第i个输入样本有效价格,ni为第i个输入样本噪声。从式(19)可看出,加性噪声部分包含在对数形式的股价中,故对数形式下的股票噪声与有效价格可定义为
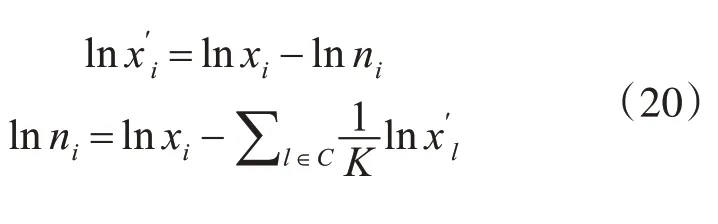

众所周知,噪声会对股价预测产生影响,若本文可在构建SVM方程时消除噪声,可进一步提升股价预测精度[12]。SNR是对信号中有效成分与噪声成分比例关系的重要描述,可有效地处理噪声。为了降低噪声干扰,本文将SNR引入。结合已有文献,我们可得到信噪比(SNR)的计算公式[13]:
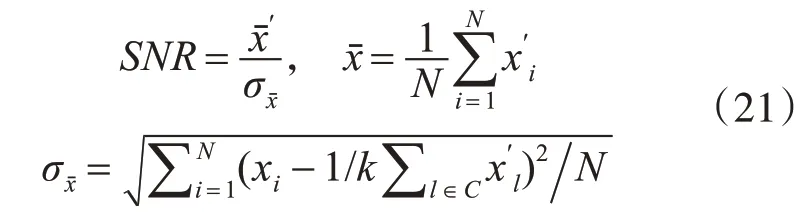
其中,N为所使用样本数据的数量,xˉ为有效价格均值,σxˉ为噪声方差。本文将SNR作为反映股票收益波动的指标,若SNR值越大,收益越稳定,风险就越小。
4 实证分析
4.1 数据预处理
本文将国内A股市场总市值排名靠前的十四只股票日数据作为研究对象,相应的时间序列日期为2009年1月1日至2018年12月31日。中国股市在这个时期经济发展呈稳健增长是选择该时期的主要原因。此外,本研究将前80%的股票数据作为训练样本,后20%作为测试样本。
考虑到参数间的巨大差异性对股价预测的影响,本研究对数据进行标准化处理:

其中,xminj为样本数据第j列的最小值,xmaxj为样本数据第j列的最大值。
4.2 评价准则
平均绝对百分比误差(MAPE)和均方根误差(RMSE)可用于评估模型的好坏,用下式表示:
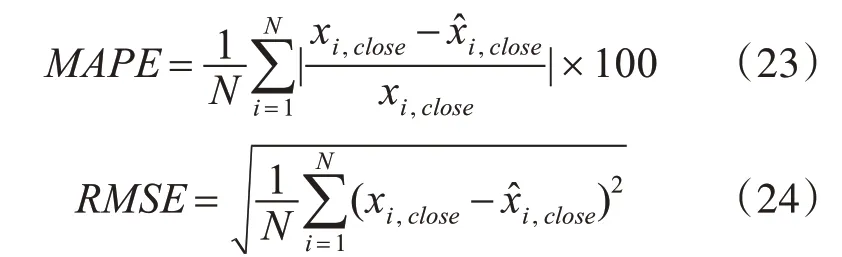
其中,N为样本数量,xi,close为第i日的股票收盘价,x^i,close为所模型预测的股票收盘价。
4.3 模型结果及分析
为了验证本文模型的有效性,我们建立基准模型进行对比分析,即模型1:为加入SNR特征向量的SVM算法的股价预测、模型2:加入SNR特征向量的SVM算法的股价预测、模型3:基于信噪比的SVM-KNN算法的股价预测和本文模型4:基于信噪比的KPCA-SVM-KNN算法的股价预测。本文采用libsvm-3.18处理SVM,同时使用10折交叉验证的网格搜索算法获得该模型的最优参数。文章分别对国内A股市场总市值排名靠前的10只股票数据进行未来1天的收盘价预测,为了简便起见,我们统一采用股票i(i=1,2,…,10)来表示14只股票。
表2为加入SNR的SVM算法采用10折交叉验证所获得的最优参数。表3为加入SNR的SVM算法和未加入SNR的SVM算法之间的股价分类准确率。
从表2可看出,所有SVM算法的系数C和K都是一致的,且系数γ的值也保持在一定范围内,从而保证对比分析和股价预测结果的准确性。

表2 加入SNR的SVM模型所使用的最优参数
从表3可看出,模型2:加入SNR的SVM算法的股价预测分类准确率要明显高于模型1:未加入SNR的SVM算法的的股价预测分类准确率。对比分析发现,本研究加入SNR后,SVM算法的股价预测分类准确率平均提高7%左右,并且对于股票2、5、6来说,加入信噪比后SVM的分类准确率可达到74%以上。本文在股价分类的基础上,借用KNN算法进行股价预测,并采用KPCA算法进行降维处理。表4显示了两个模型的股价预测误差。从表4可看出,模型3:SVM-KNN算法的股价模型预测和模型4:KPCA-SVM-KNN算法的股价预测模型均较好地反映了时间序列,而且可以清楚地观察到KPCA-SVM-KNN算法的股价预测误差更低,说明KPCA-SVM-KNN算法的股价预测结果相较于SVM-KNN算法更好。此外,本研究还发现:1)KPCA-SVM-KNN算法对于股票2的预测结果最好,因为不管相对于MAPE还是RMSE,它的预测误差都是最小的;2)除了股票6和7之外,其他股票的股价预测误差都小于1。

表3 模型1与模型2[18]的分类准确率 百分比/%
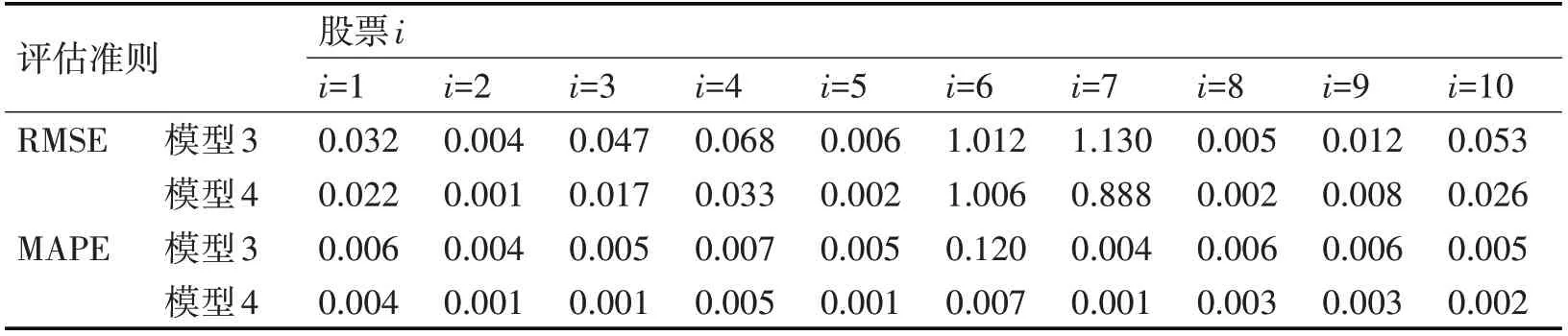
表4 模型3[7]算法与模型4的预测误差
5 结语
本文提出了基于信噪比的KPCA-SVM-KNN的股价预测模型,并借助国内A股市场股票数据进行股价预测。结果表明:1)信噪比的创建可更好地克服股价变化趋势中所含的噪声信息带来的股票分类结果的偏移,有效地降低噪声信息对预测结果的干扰,进而提高股价预测的分类准确率;2)KPCA算法不仅可以实现降维,而且在一定程度上消除输入变量之间的多重共线性对分类超平面的影响。通过KPCA算法的引入,本研究既可提高原有的SVM-KNN算法的运行速度,又进一步降低股票预测误差。
