相邻扶正器间抽油杆柱纵横耦合振动特性仿真*
2022-05-10智勤功
智勤功
(中国石化胜利油田分公司石油工程技术研究院)
0 引 言
抽油机举升是油田最常见的采油方式[1]。受多种实际因素的影响,油井井眼轨道多为存在较大弯曲的空间曲线,即油井为定向井[2]。由于井眼轨道的影响,抽油杆柱在井下呈弯曲状态。抽油机运行过程中,抽油杆柱在顶端周期性位移激励和底端周期性载荷激励的作用下产生轴向振动,轴向振动又导致了杆柱各截面轴向内力的波动。在轴向力与弯曲井眼的共同作用下,抽油杆柱在弯曲井眼轨道内产生横向振动,即抽油杆柱的动力学行为是纵横耦合振动。抽油杆柱纵横耦合振动导致油井存在较大的杆管接触力,进而导致油井产生杆管偏磨现象。油井实际运行情况表明,杆管偏磨导致的抽油杆柱与油管失效是油井检泵作业的主要原因之一。在抽油杆上布置扶正器是最常用的杆管防偏磨措施,因此优化扶正器的配置方案一直是油田关注的重点。
以研究对象分类,目前关于扶正器优化配置的设计方案主要分为两类:①以整体抽油杆柱为研究对象,通过静力学或动力学仿真模型计算杆管接触力,以杆管接触力的仿真结果为依据优化扶正器的配置方案[3-7];②以相邻扶正器之间抽油杆柱为研究对象,将其简化为考虑或不考虑初弯曲的简支梁模型,以杆柱受压不失稳或杆体、接箍不与油管接触为约束条件,优化扶正器的布置间距[8-13]。相较于第一类设计方案,第二类设计方案以其模型简单易于理解、计算便捷的优势而被大众所接受。目前第二类设计方案中仅考虑了抽油杆柱在最大压力下的静力变形,但对于实际问题来说,抽油杆柱在交变轴向载荷的作用下存在横向振动,横向振动将影响杆柱的横向变形,进而影响扶正器的优化配置。因此有必要建立两相邻扶正器之间的抽油杆柱纵横耦合振动仿真模型,并分析杆柱横向振动对杆柱横向变形的放大作用。
本文基于纵横弯曲梁理论,建立了两相邻扶正器之间抽油杆柱在交变轴向载荷激励下的纵横耦合振动仿真的力学与数学模型。采用空间离散——时间连续与数值积分相结合的方法进行数值求解,实现了两扶正器之间杆柱纵横耦合振动的仿真计算。通过动力学仿真结果与静力学仿真结果的比较,证明了优化扶正器配置时考虑抽油杆柱横向振动的必要性。以上述研究为基础,建立了扶正器配置间距优化模型,实现了扶正器配置间距的优化设计。
1 杆柱纵横耦合振动力学与数学模型
抽油杆柱长度达上千米,为防止杆管偏磨,通常在抽油杆上布置扶正器[14]。在油井工作过程中,抽油杆柱在交变轴向载荷与自重的影响下产生纵横耦合振动。为简化研究,本文取两相邻扶正器间的抽油杆柱为研究对象,分析抽油杆柱的振动特性。
为便于研究,同时也为突出本文的研究重点,做如下简化和假设:①抽油杆柱为均质弹性体;②杆柱各横截面切应力始终处于杆柱轴线的法平面内;③将杆柱两端扶正器简化为铰支约束;④仅考虑井斜角的变化,忽略方位角的变化。
1.1 抽油杆柱纵横耦合振动方程
在上述假设条件下,建立相邻扶正器间抽油杆柱纵横耦合振动力学模型,如图1所示。

图1 抽油杆柱纵横耦合振动力学模型Fig.1 Mechanical model of longitudinal and transverse coupling vibration of sucker rod string
对于相邻扶正器间抽油杆柱来说,扶正器约束了杆柱的横向位移,因此可以将杆柱两端扶正器简化为铰支约束。由于杆柱存在纵向振动,所以其中一端为固定的铰支约束,另一端为可滑动的铰支约束,且受交变集中轴向载荷的作用。此外杆柱还受分布载荷的作用。图1中:P(t)为t时刻作用于杆柱一端的轴向载荷,以拉力为正;q(s,t)为杆柱所受轴向分布载荷;qub(s,t)为杆柱所受横向分布载荷。微元两端的集中力Fe(s,t)可以分解到对应井眼轨道的切线方向与主法线方向。微元横向所受外力可分解到对应井眼轨道的主法线方向。
基于微元受力可以得到以矢量表示的杆柱纵横耦合振动的运动微分方程:
fe(s,t)ds
(1)
其中:
(2)
式中:ρ为抽油杆密度,kg/m3;A为抽油杆横截面积,m2;e(s,t)为t时刻杆柱任意截面s处的节点在井眼切线方向上的位移,m;τA(s)为井眼轨道任意截面s处的切向量;u(s,t)为t时刻杆柱任意截面s处的节点在井眼主法线方向上的位移,m;nA(s)为井眼轨道任意截面s处的主法线向量;Feτ(s,t)为t时刻杆柱任意截面s在切向方向上的内力,N;Fen(s,t) 为t时刻抽油杆柱任意截面s在主法线方向上的内力,N;kA(s)为井眼轨道任意截面s处的斜率,m-1;feτ(s,t)为t时刻抽油杆柱任意截面s处切向所受外力,N/m;fen(s,t)为t时刻抽油杆柱任意截面s处主法线方向所受外力,N/m;(Feτ)s为Feτ对s求一阶偏导,N/m;(Fen)s为Fen对s求一阶偏导,N/m。
忽略方位角变化时,井眼轨道的斜率表达式为:
(3)
式中:α(s)为井眼轨道任意截面s处的井斜角,(°)。
对式(1)进行简化,可以得到杆柱纵横耦合振动的运动微分方程:
(4)
在小变形假设下,由弹性力学可知Feτ和(Feτ)s的表达式[15]:
(5)
式中:es为e对s求一阶偏导;ess为e对s求二阶偏导,m-1; (kA)s为kA对s求一阶偏导,m-2;us为u对s求一阶偏导。
通过微元受力分析列弯矩平衡方程,进而求解内力之间的关系,则有:
(6)
化简得:
Ms+[Fen(1+es)-Feτus]bA=0
(7)
其中:
(8)
式中:E为抽油杆材料的弹性模量,Pa;I为抽油杆的抗弯惯性矩,m4;usss为u对s求三阶偏导,m-2。
将式(8)带入式(7)进行计算,求得Fen的表达式:
(9)
式(9)对s求偏微分可得如下公式:

(10)
式中:uss为u对s求二阶偏导,m-1;ussss为u对s求四阶偏导,m-3;(kA)ss为kA对s求二阶偏导,m-2。
杆柱所受分布外力可表示为:
(11)
式中:μ为阻尼系数,Pa·s。
1.2 边界条件
杆柱两端的边界条件可表示为:
(12)
对于实际抽油机井,杆柱底端集中轴向载荷受抽油泵工作状态的影响。为简化模型,本文基于正弦曲线构造与其形态类似的轴向载荷,其表达式为:
(13)
其中:
(14)
式中:T为激励周期,s;Tt为载荷最大值所持续的时间,s;Tb为载荷最小值所持续的时间,s;n为抽油机冲次,min-1。
1.3 初始条件
假设抽油杆柱初始状态时,杆柱轴线与井眼轴线重合。初始条件可表示为:
(15)
2 纵横耦合振动仿真方法
抽油杆柱纵横耦合振动的仿真模型为变系数的偏微分方程,无法求得方程的解析解。本文首先采用空间离散——时间连续与数值积分相结合的方法将偏微分方程的求解问题转化为常微分方程的求解问题,然后采用四阶龙格库塔法进行求解。其求解形式如下:
(16)
式中:y(4i-3)为第i个节点的轴向位移,m;y(4i-2)为第i个节点的轴向速度,m/s;y(4i-1)为第i个节点的横向位移,m;y(4i)为第i个节点的横向速度,m/s;Feτ,i为第i个节点处的轴向内力,N;Feτds,i为Feτ,i对s偏导数的差分形式,N/m;Fen,i为第i个节点处的切向内力,N;Fends,i为Fen,i对s偏导数的差分形式,N/m;kA,i为第i个节点所对应的井眼斜率,m-1;feτ,i为第i个节点处的轴向分布力,N/m;fen,i为第i个节点处的横向分布力,N/m。
以差分公式为基础,式(16)中Feτ,i、Feτds,i、Fen,i、Fends,i、feτ,i和fen,i的数值可分别依据式(10)、式(14)、式(15)和式(16)求得。
式(16)的初始条件为:
y=0
(17)
对式(16)进行求解,即可得到抽油杆柱的纵横耦合振动仿真结果。图2为杆柱纵横耦合振动仿真计算流程图。
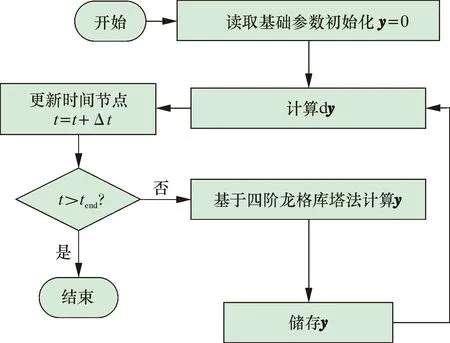
图2 计算流程图Fig.2 Calculation process
3 扶正器配置间距优化模型
在抽油杆上配置扶正器的目的是防止发生油井的杆管偏磨现象,其实现方法就是防止杆柱与油管接触,在这种思路下建立了扶正器配置间距的优化模型。优化模型的设计变量就是两相邻扶正器之间的配置间距。优化目标是在满足杆管不接触的约束条件下,两相邻扶正器之间的配置间距最大,可表示为:
Lop=max(L)
(18)
式中:Lop为在满足杆管不接触的约束条件下两相邻扶正器之间的最大配置间距,m;L为两相邻扶正器之间的配置间距,m。
优化模型的约束条件为抽油杆柱与油管不接触,即杆柱最大横向变形量小于杆管间隙,即有:
max(u)<δrt
(19)
式中:δrt为杆管间隙,m。
4 仿真实例与仿真分析
分别采用本文建立的杆柱纵横耦合振动仿真模型与杆柱静力学仿真模型(去除公式(4)中的动力学项与公式(11)中的阻尼项即可得到静力学模型)对杆柱的横向变形进行仿真,通过仿真结果对比说明在优化扶正器配置时考虑杆柱振动的必要性。为了进行对比,首先对动力放大系数进行定义:
(20)
式中:u0为静力学模型所得杆柱横向位移,m。
4.1 基本参数
表1为抽油杆柱纵横耦合振动仿真的基本参数。图3为杆柱一端轴向集中载荷的变化规律。

表1 仿真参数Table1 Simulation Parameters

图3 轴向集中载荷Fig.3 Axial concentrated load
4.2 仿真结果分析
以表1中参数为基础,采用静力学模型进行仿真,得到抽油杆柱受600 N压力时,杆柱的静力学仿真变形结果,如图4a所示;采用动力学模型进行仿真,得到一个周期内抽油杆柱横向位移的仿真结果,如图4b所示。
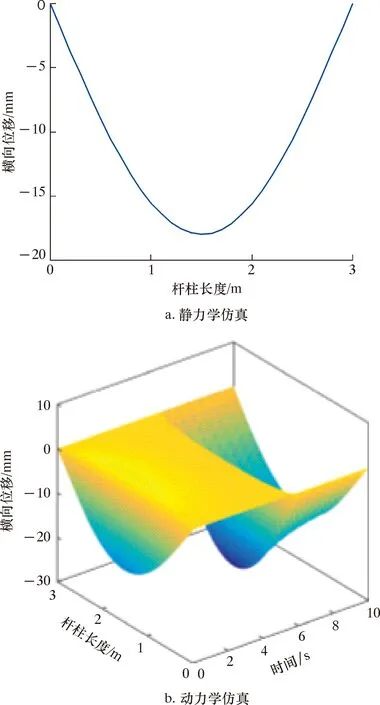
图4 杆柱横向变形仿真结果Fig.4 Simulation results of lateral deformation of rod
由图4可以看出:静力学模型仿真结果抽油杆柱最大横向变形量为17.96 mm;动力学模型仿真结果抽油杆柱最大横向变形量为26.10 mm;相对静力学模型仿真结果来说,动力学模型仿真结果的抽油杆柱横向变形更大,因此在进行扶正器布点设计时,采用动力学仿真模型分析杆柱变形更为合理,所得结果更为可靠。
4.3 敏感度分析
杆柱振动受多方面的因素影响。本节分别从冲次(激励周期)、最小激励载荷、最大激励载荷、最小载荷持续时间与井斜角5个方面分析影响杆柱横向振动的敏感因素。
4.3.1 轴向激励对杆柱振动的影响
通过调整冲次,计算得到不同冲次下杆柱最大横向变形。杆柱横向变形动力放大系数随冲次的变化曲线如图5所示。

图5 动力放大系数随冲次的变化曲线Fig.5 Variation of dynamic amplification coefficient with stroke
由图5可以看出,随着冲次的增大,杆柱横向振动的动力放大系数逐渐增大,即冲次越高对杆柱横向振动的影响越明显。
保证激励最大载荷不变,调整激励的最小载荷进行仿真计算,得到动力放大系数随激励最小载荷的变化曲线,如图6所示。

图6 动力放大系数随最小激励载荷的变化曲线Fig.6 Variation of dynamic amplification coefficient with minimum excitation load
由图6可以看出,动力放大系数随最小载荷的增大而减小。这是由于最小激励载荷增大后,激励幅值降低,杆柱振动减弱。
保证最小激励载荷不变,通过调整最大激励载荷进行仿真计算,得到动力放大系数随最大激励载荷的变化曲线,如图7所示。

图7 动力放大系数随最大激励载荷的变化曲线Fig.7 Variation of dynamic amplification coefficient with maximum excitation load
由图7可以看出,动力放大系数随着最大激励载荷的增大而增大。相较于最大激励载荷,杆柱最大横向变形对最小激励载荷的变化更敏感。
保证最大、最小激励载荷与激励幅值不变,通过调整最小激励载荷所持续的时间,计算得到不同激励形态下杆柱最大横向变形,进而得到动力放大系数随最小激励载荷持续时间Tb的变化曲线,如图8所示。
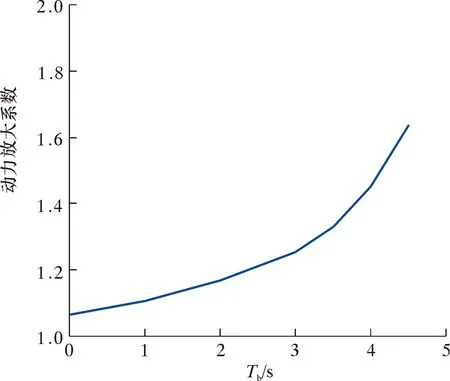
图8 动力放大系数随Tb的变化曲线Fig.8 Variation of dynamic amplification coefficient with Tb
由图8可以看出,动力放大系数随着最小激励载荷持续时间的延长而增大。这是由于最小激励载荷持续时间的延长,导致集中载荷由最大值变为最小值的速度加快,进而导致杆柱振动加剧。
4.3.2 井眼轨道对杆柱振动的影响
通过调整井斜角,计算得到不同井斜角下杆柱的最大横向变形,进而得到动力放大系数随井斜角的变化曲线,如图9所示。
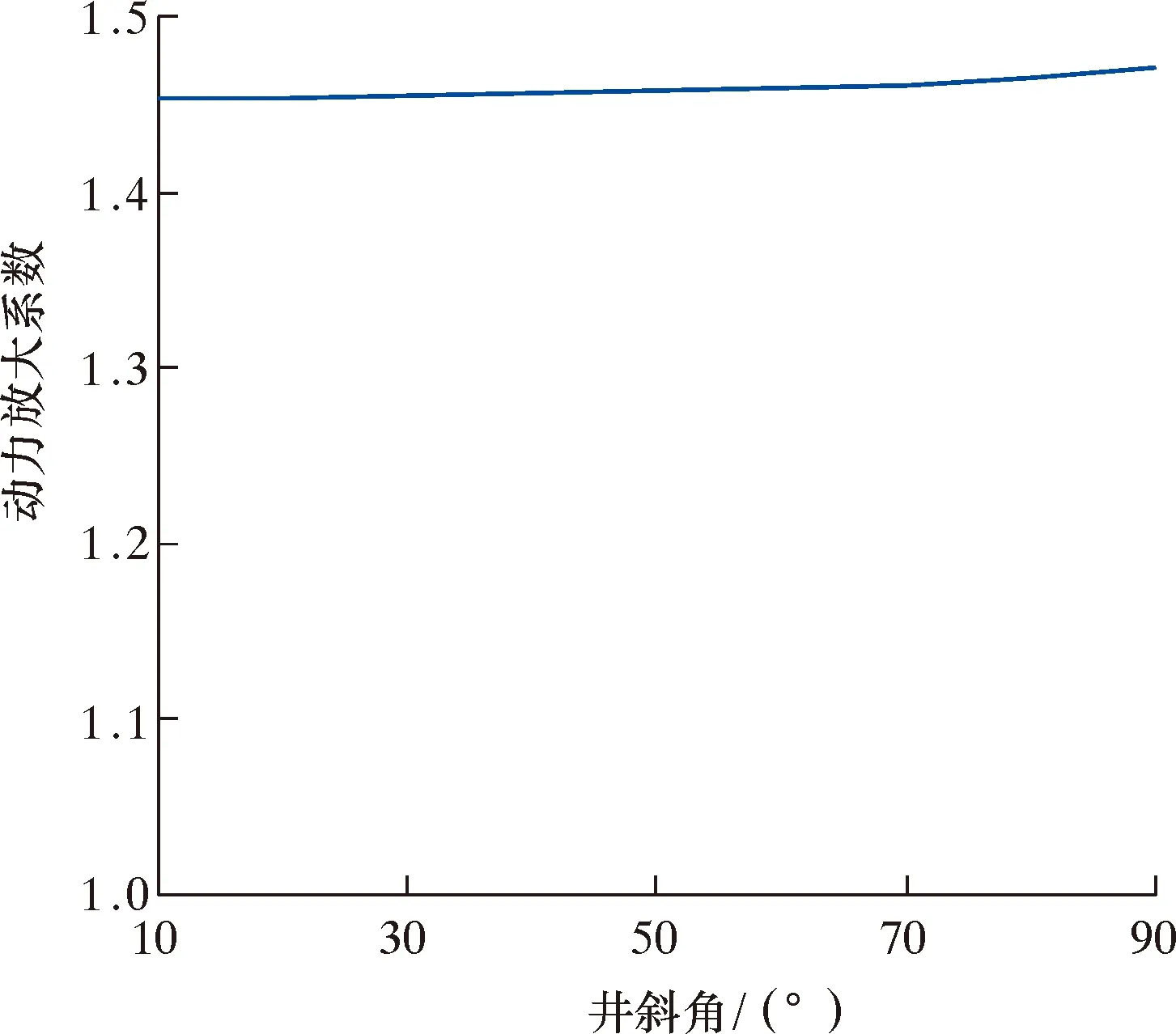
图9 动力放大系数随井斜角的变化曲线Fig.9 Variation of dynamic amplification coefficient with deviation angle
由图9可以看出,随着井斜角的增大,动力放大系数逐渐增大。但相较与其他参数来说,井斜角变化对动力放大系数的影响并不明显。
4.4 扶正器配置间距优化实例
由材料力学可知,杆柱的最大受压载荷(即轴向最小集中载荷)是影响杆柱横向变形的主要因素。为此,本小节以表1中的基本参数为例,分别调整P0与P1的数值以达到保证轴向最大集中载荷不变、最小集中载荷改变的目的,进而通过优化计算,得到在同一轴向最大集中载荷下,扶正器最优配置间距随轴向最小集中载荷的变化曲线,结果如图10所示。
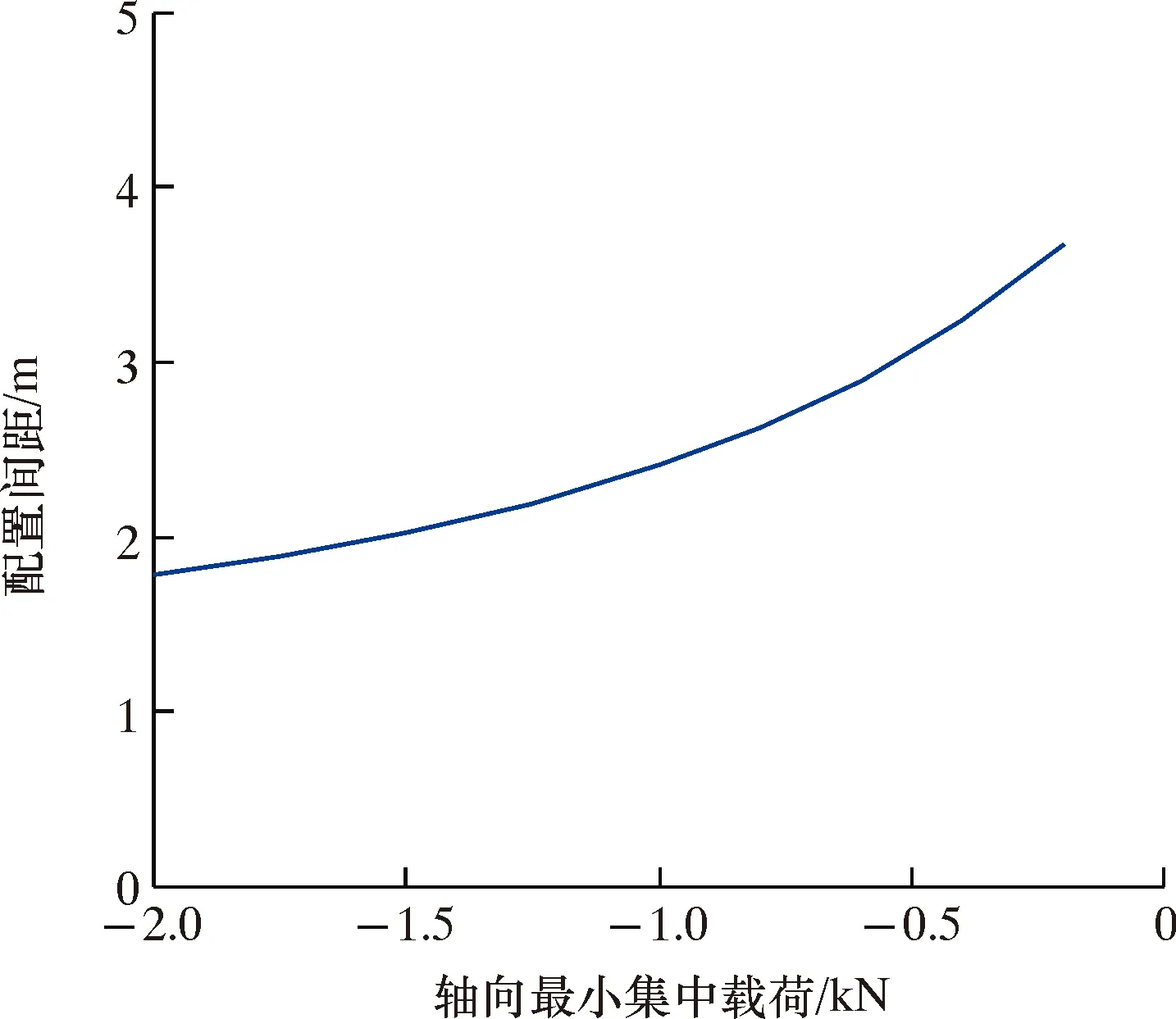
图10 扶正器最优配置间距随轴向最小集中载荷的变化曲线Fig.10 Variation of optimal spacing of centralizers with minimum axial concentrated load
由图10可以发现,扶正器最优配置间距随轴向最小集中载荷的减小而缩短。这说明本文建立的优化模型可以实现对扶正器最优配置间距的优化设计。结合抽油杆柱实际受力可以知道,杆柱的受压段为杆管偏磨的危险点,在配置扶正器时,在杆柱底端应适当加密扶正器的布置。
5 结 论
(1)考虑交变轴向载荷激励,基于纵横弯曲梁理论,建立了弯曲井眼轨道内两扶正器之间杆柱纵横耦合振动仿真的力学与数学模型。采用数值方法实现了定向井两扶正器之间杆柱纵横耦合振动的仿真计算。
(2)仿真计算结果表明,相对于静力学模型仿真结果,动力学模型仿真结果的杆柱横向变形更大。因此在进行扶正器布点设计时,采用动力学仿真模型更加合理,所得结果更为可靠。
(3)杆柱的轴向载荷激励与杆柱的初弯曲是影响杆柱横向位移动力放大系数的主要原因。
(4)建立了扶正器配置间距优化模型,实现了两扶正器间最优配置间距的优化设计。研究结果为油井防偏磨设计提供思路,对降低原油开采成本具有实际意义。
