城市震后应急食品供应优化调配模型研究

2022-05-10刘姝昱樊毫军曹春霞

自然灾害学报 2022年2期

刘姝昱，刘鑫，刘涛，樊毫军，曹春霞

（天津大学应急医学研究院，天津 300072）

引言

近年来，全球范围内地震灾害频发，对灾后应急救援管理工作提出了新的挑战，尤其是强震灾害（震级≥6 级的地震灾害）发生在人群密集、高层建筑物集聚的城市地区时，多造成重大的人员伤亡及严重的经济损失［1-2］。我国《国家自然灾害救助应急预案》、《国家地震应急预案》及《中华人民共和国突发事件应对法》等指导文件中明确提出：灾害发生后应当紧急调拨应急物资以保障受灾人员基本生活。灾后应急救援过程中，合理有效的应急物资分配不仅有助于降低人员及经济损失，同时还可避免对其造成二次伤害，有助于社会的和谐稳定与国家的可持续发展。因此，针对城市震后的应急物资优化调度研究具有十分重要的现实意义与实用价值。

灾后应急物资调度依据供应点与需求点数量的多少，可将其划分为单供应点-单需求点、多供应点-单需求点、单供应点-多需求点和多供应点-多需求点4 大类。刘春林等［3-4］针对灾后单需求点应急物资调度问题，提出了“应急时间最短、出救点数量最少”的一次性消耗系统多目标优化模型，并借助模糊优化算法解决了多出救点的组合优化问题。罗朝晖等［5］建立了单种类、多需求点的军械物资紧急调运优化模型，通过数学逻辑推导给出了相应的解析算法，为物资调配指挥人员提供了一种量化参考。陈达强等［6］考虑应急物资供应过程中出救点供应量与需求点需求量随时间呈现动态变化趋势的特点，提出了应急响应时间最少、带时变供求约束的物资分配模型。魏国强等［7］针对应急物资运输时间不确定性问题，提出了基于区间数界定应急响应时间的多需求点物资优化调度模型。张国富等［8］针对多供应点-多需求点应急物资调配问题，构建了并发分配与调度的多目标优化模型。吕伟等［9］针对多受灾点物资紧缺且各类应急物资受不同时间窗约束的现实，以最大化应急供应时间、需求满意度为目标，同时兼顾公平性原则，构建了基于综合时间窗约束的应急物资调配模型，为救灾供应方案提供了新思路。综上所述，目前灾后应急物资供应优化调配研究虽取得了一定研究成果，但多局限于不区分物资类别的单供应点-多需求点或多供应点-单需求点间的优化调配，针对单一种类物资的多供应点-多需求点优化调配模型仍需进一步研究。

民以食为天，震后灾民由于恐慌感加重而导致基本的饮食需求也愈加突出。应急食品作为一类可维持人体基本生存且便于运输的应急物资，是灾后食品供应的首要选择，因此，应急食品供应便成为了灾后应急供应的重中之重［10］。灾后应急食品供应属于应急物流系统范畴，由于其以实现应急食品从供应点至需求点“时空”转移为目的，除了具备应急物流突发性、不确定性、弱经济型、时间紧迫性等一般性特点，同时还具备以下显著特点：（1）时效性，强震等突发灾害发生后，应迅速对受灾区群众进行应急食品供应，以保障其基本生存；（2）连续性，灾区群众对应急食品需求及应急食品消耗均是连续的；（3）阶段性，灾害发生初期以方便类应急食品为主，中后期营养型、能量型应急食品则显著增加；（4）安全性，灾区所需应急食品具有严格的安全性要求。

基于此，文中以强震灾害为例，首先分析总结了城市震后受灾面积与应急食品需求模型，为应急食品供应优化调配模型的构建提供相应数据支持；其次，参考应急物资调配相关模型，针对应急食品多供应点-多需求点供应情境，考虑满足各需求点需求数量约束，构建了以应急响应时间最短为目标的应急食品供应优化调配模型，旨在解决城市强震后应急食品多供应点-多需求点间的供应问题，缩短应急响应时间，实现震后应急食品供应最优调配；最后，通过仿真算例验证了所构模型的正确性与高效性。

1 应急食品需求分析

随着中国城市化进程的加快，城市已成为当今社会的发展常态。城市中人群、社会财富高度密集，当遭受强震灾害袭击时多伴随房屋建筑倒塌、基础设施瘫痪等严重灾害损失，导致大量人员无家可归。由于地震灾害的突发性，受灾群众无法在短时间内被疏散至安全地区。为降低受灾群众遭受二次灾害的风险，保障其人身安全，政府等相关部门亟需在短时间内对受灾群众进行统一安置与集中救助［11］。城市应急避难所作为一类预先经由科学规划及管理，集通讯、电力、物流、人流、信息流为一体的重要空间资源储备，肩负着灾民避险栖身与救援部门集中救助的双重职能，是灾后应急安置的首要选择［12-13］。此外，为进一步巩固防灾减灾能力建设，我国确立了应急物资三级分层储备制度，并相继设立了24 个中央级应急物资储备库及相应省市、区县级应急物资储备库［14-15］。鉴于上述状况，文中以应急食品储备点作为应急食品供应点，应急避难场所作为应急食品需求点进行应急食品供应调配优化模型的构建。

在我国，受灾面积通常是指地震烈度VI 度及VI 度以上的区域面积，且受灾范围内建筑物、基础设施等多受损严重。同时，《中华人民共和国防震减灾法》中明确规定：建筑物新建、改建、扩建应按国家有关规定达到抗震设防要求，查询可知下文涉及某直辖市辖区建筑物抗震设防烈度最低为VII 度［16］。文中参考上述抗震设防烈度与受灾面积定义认为该直辖市强震灾害受灾面积应为地震烈度Ⅷ度以及Ⅷ度以上区域面积，且受灾范围内应急食品储备点及应急避难场所不再使用。强震灾害发生后，相关政府部门可在地理信息系统（GIS）等技术手段支持下，兼顾应急避难所最大可容纳人数与受灾区就近原则对受灾范围之外的应急避难场所进行筛选，最终获取可用应急避难场所列表。为便于需求量计算，本文依据选定各应急避难场所最大可容纳人数进行应急食品数量需求计算。其中，应急食品需求量计算关系为：应急食品需求量=受灾人数×赈灾救助标准，赈灾救助标准为每人每天0.5 kg应急食品［17］。

2 问题描述

强震灾害发生后，政府主导下的储备点调用是最常用的应急物资供应方式之一，普遍应用于重特大自然灾害后应急响应过程中。基于该供应方式，本文构建了包含应急食品供应点、应急食品需求点两层结构的应急食品供应体系。进行灾后应急食品供应时各供应点同时启动，每个应急食品供应点可同时满足多个应急食品需求点，每个应急食品需求点可由多个应急食品供应点供应（如图1）。此外，考虑到灾后应急食品供应时效性特征，响应时间越短，供应效果越好。因此，本文确定需要优化的问题为应急食品供应调配方案，在满足各需求点需求数量的前提下，以应急响应时间最短为目标，构建城市强震后应急食品供应优化调配模型［18-20］。

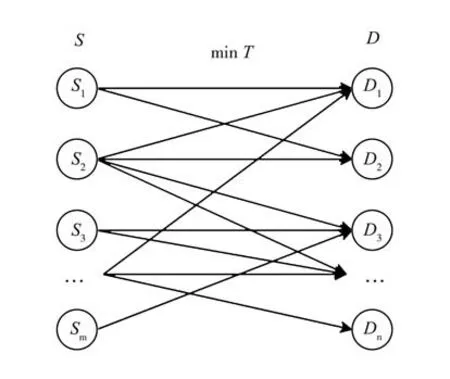
图1 应急食品供应示意图Fig.1 Schematic diagram of emergency food supply

为便于模型的构建与求解，本文假设了以下条件：

（1）有m个供应点和n个需求点，且不区分应急食品具体种类；

（2）m个供应点的初始应急食品存储量及n个需求点的需求数量已知，且各供应点应急食品总存储量充足；

（3）m个供应点至n个需求点的运输响应时间已知；

（4）受灾区域内的应急食品供应点、应急避难场所受强震灾害波及，不参与应急食品供应过程。

3 模型构建

（1）符号说明

Si表示应急食品供应点集合，i=｛1，2，...，m｝；Dj表示应急食品需求点集合，j=｛1，2，...，n｝；X表示n个应急需求点的应急食品需求总量；xi表示供应点Si的应急食品供应量，xi＞0；xj表示需求点Dj的应急食品需求量，xj＞0；xij表示供应点Si对需求点Dj的实际供应量，xij≥0；tij表示供应点Si至需求点Dj运输响应时间，tij＞0；T表示应急食品供应时间即应急食品从应急供应点被运送至对应需求点的最长运输响应时间，T＞0；yij∈｛0，1｝由xij决定，取1表示供应点Si至需求点Dj的路径被使用，否则取0。

（2）模型建立

目标函数表示应急食品供应所花费时间最短；约束条件式（1）表示各应急食品供应点对各需求点的实际供应量应不大于原有储备量；约束条件式（2）表示各应急食品供应点的实际供应量恰好等于需求点的需求量；约束条件式（3）表示各供应点至需求点的运输响应时间均不大于应急食品供应的应急响应时间；约束条件式（4）表示决策变量yij的取值，当xij＞0时，yij值为1，当xij=0时，yij值为0。

4 算例分析

已知某直辖市设有中央级（1个）、省市级（1个）、区县级（16个）三级应急食品储备库，各储备库中均储备有足量应急食品物资以满足强震灾害后应急食品物资调用。现假设该市某区发生7.0级强震灾害，造成10万人受灾，且该区应急食品供应点因灾害无法正常使用，故需调用其他各区应急食品储备以满足灾区应急食品需求，各应急供应点供应能力详见表1。同时依据应急避难场所“就近选取”原则，将受灾群众分散安置在灾区附近的5 处应急避难场所内等待救援，各应急避难所最大可容纳人数及各应急避难所应急食品需求数量详见表2。

表1 应急食品供应点供应能力Table 1 Supply capacities of emergency food depots kg

表2 各应急避难场所应急食品需求量Table 2 Emergency food demand of emergency shelterskg

基于Sioux Falls 网络进行运输时间获取，选取节点10 为受灾中心点，节点1，2，3，4，5，6，7，8，12，13，14，18，19，20，21，22，23依次设为17个应急食品供应点，节点9，11，15，16，17依次设为5个应急食品需求点，每条路段标记的是对应序号，如图2 所示。已知强震灾害可导致路网存在不同程度受损，因此，在文中以各路段两端点与受灾中心点平均距离为依据进行道路受损等级划分，分别设为0.3，0.5，0.7。其中，距受灾中心点平均距离L＜10 时，路段受损等级最大为0.7；距受灾中心点平均距离10≤L＜20 时，路段受损等级为0.5；距受灾中心点平均距离L＞20 时，路段受损等级则为0.3。在此基础上，对每条路段生成正态分布均值为t1，标准差为0.3 的随机数t2（t2＞0）；如果t2＞0.95，则认为该路段无法通行；否则，则认为对应路段运输时间增加n×t1+t2（本实验中，n=4），最终获取各应急食品供应点至应急食品需求点最短运输时间，并使其符合实际情况，如表3所示。

表3 灾后运输响应时间Table 3 Post-disaster transportation response time min

图2 Sioux Falls网络Fig.2 Sioux Falls network

采用Gurobi求解器编程求解，最终得到该应急食品供应方案应急响应时间为296 min，供应方案为：供应点S1，S4为需求点D1进行应急食品供应；供应点S3，S14为需求点D2进行应急食品供应，供应点S1，S6，S8，S10，S11，S15，S17，为需求点D3进行应急食品供应，供应点S1，S4为需求点D4进行应急食品供应，供应点S2，S5，S6，S7，S9，S12，S13，S16，S17为需求点D5进行应急食品供应，各供应点对需求点的具体供应数量详见表4。

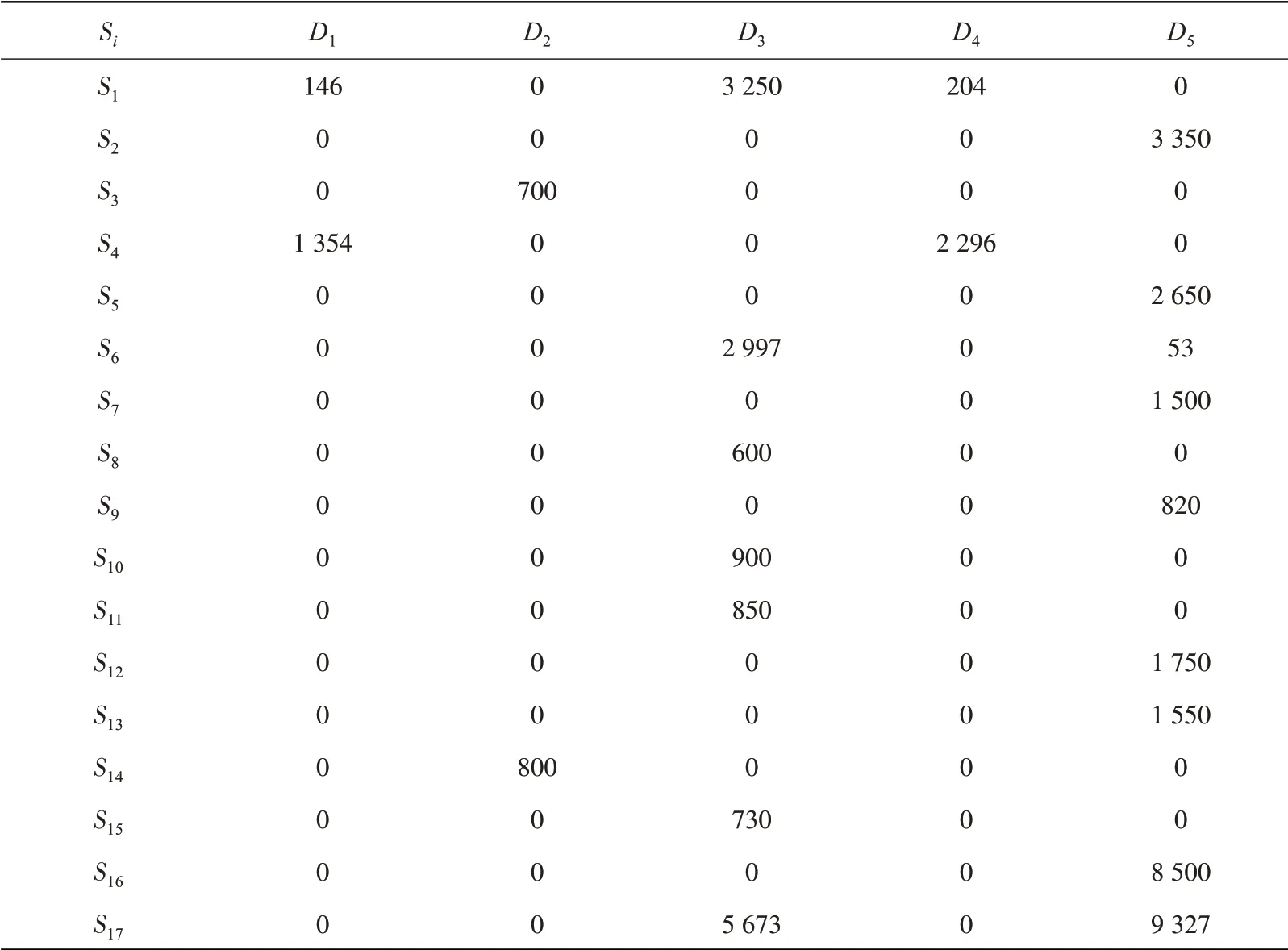
表4 应急食品供应方案Table 4 Emergency food supply scheme kg

进一步分析该直辖市应急避难场所属性数据了解到，截至2021年，该市各区共设有2 395个应急避难场所，其中，约91.4%应急避难场所最大可容纳人数不足10 000人，可容纳10万人以上的大型应急避难场所仅有4个。为更切合这种小型应急避难场所广泛分布，大中型应急避难场所稀疏分布的现实状况，笔者将应急避难场所扩增至100 处以验证优化调配模型的适用性。实验结果表明，模型计算时间为0.02 s，且供应方案中存在多供应点-多需求点调配关系，这表明文中所构模型在处理存在较多需求点的真实案例时同样具有较强的适用性。