深度网络去相关层归一化技术研究

王志扬，袁 旭，沈项军，赵增民，季 彬

1(江苏大学 计算机科学于通信工程学院，江苏 镇江 212013)

2(常州云众智能科技有限公司，江苏 常州213000)

1 引 言

如今，深度神经网络在图像分割[1]，文本分类[2]，图像分类[3]等领域获得了巨大的成功.这是因为深度网络通过多层非线性变换，其特征表达能力远强于传统浅层特征表达方法.但是随着网络深度的加深，过拟合的风险也越来越大，另外网络中也随之产生了梯度消失和梯度爆炸等难题，这些问题使得模型的训练变得很困难.现阶段，类似于权重衰减(Weight decay)[4]和Dropout[5]等技术已经被广泛的应用到网络训练中来解决上述的问题.这些技术虽然能够提升网络的泛化能力，但是经常牺牲优化效率来换取精度的提升，这意味着有时需要训练更多的epoch来获得更好的性能.如何高效的训练深度神经网络现阶段是一个具有挑战性的问题.

近年来，归一化(Normalization)的提出有效的避免了梯度爆炸和梯度消失的问题.在神经网络中，如果某个特征数量级过大，在经过激活函数时，就会提前进入激活函数的饱和区间，导致网络学习提前结束.数据归一化技术可以重构原始的数据分布，使之落入一个小的特定区间，便于不同单位或量级的指标进行比较和加权.基于这一特点将其加入深度神经网络的学习能够在解决上述问题的基础上进一步提升网络的收敛速度和精度.其中批归一化(Batch Normalization，BN)[6]作为一个加速网络训练的技术已经被广泛的用于最新的网络中，但是其需要设置合理的Batchsize才能有效的评估均值和方差，这也意味着批归一化不适用于Batchsize很小的分布式模型.另一方面，在递归神经网络(Recurrent Neural Networks，RNNs)[7，8]中递归神经元的总输入通常随序列长度而变化，因此在递归神经网络中批归一化表现的并不理想.

为了能够更好的训练递归神经网络，Ba等人提出了层归一化(Layer Normalization，LN)[9]，该方法通过中心化和缩放网络中神经元输入，使得一层中不同的神经元具有相同的均值和方差来帮助网络稳定训练.与批归一化不同，层归一化对Batchsize的大小没有任何限制，它可以适用于Batchsize为1的时候.由于该方法的简单性和有效性，层归一化已经成功的运用在各种深度模型上，并在不同任务上实现了更好的性能[10-12].尽管层归一化在训练序列模型上非常有效，但是在视觉识别方面只取得了有限的成功.针对卷积神经网络(Convolutional Neural Networks，CNNs)[13，14]，何等人在2018年提出了组归一化(Group Normalization，GN)[15]来提升层归一化在视觉识别方面的性能.大量的研究表明，组归一化在Batchsize较小时具有比层归一化更好的性能，这给Batchsize较小时的模型训练提供了很好的优化方案.

不同于组归一化的将通道进行分组，我们从数据分布的角度出发来提升层归一化的性能.以多通道的图像数据为例，虽然现有层归一化技术能够让不同通道的像素点具有相同的均值和方差，但是没有降低原图像中相邻像素点之间的相关性(图1上)，这意味着用于训练时的输入是冗余的.基于此，本文进一步提出了去相关的层归一化(Decorrelated Layer Normalization，DLN) 来改善层归一化的优化性能.所提方法通过对单个样本所有通道加入白化操作，在保留原归一化的基础上进一步减少了输入特征之间的相关性，从而降低了输入数据的冗余并最终提升层归一化的优化效果.与传统的层归一化对比如图1所示，下方去相关层归一化能够使得不同通道的数据特征表达具有独立同分布的特点.为了能够使得白化后的数据更接近原始数据，本文采用ZCA白化[16]可最大程度地减少欧氏距离下由白化引起的失真[16，17].实验结果表明，我们的方法相对于其他归一化方法在Batchsize较小时有着更好的效果.

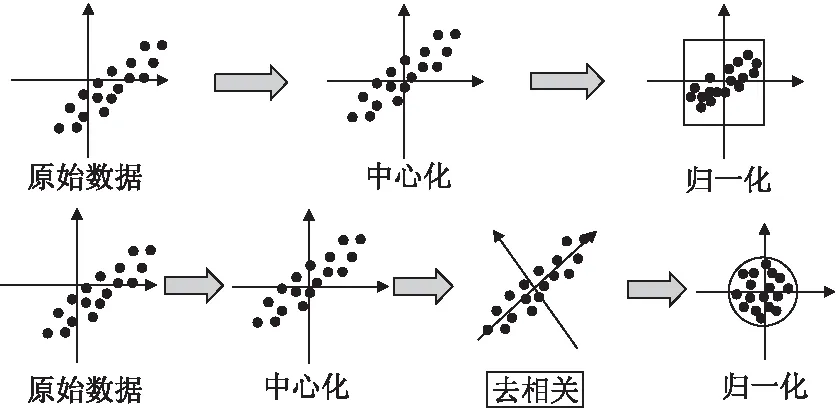
图1 层归一化与去相关层归一化

2 相关工作

归一化技术因其可以提高网络的泛化能力而被广泛用于各种深度网络体系结构中.归一化技术可以分为数据归一化和权重归一化两个方向，针对数据归一化2015年提出了BN[6]有效的减少了ICS(Internal Covariate Shift).BN通过一定的规范化手段，把每层网络输入的分布重塑到均值为0方差为1的标准正态分布.许多实验已经证明批归一化可以优化和提升深度网络的收敛，并由于它的随机不确定性也可以作为一个正则化器有益于网络泛化.2016年，Hinton等人提出了LN[9]解决了BN不适用于小Batchsize的情况，区别于BN，LN层中的所有隐藏单元共享相同的归一化项，但是不同的训练用例具有不同的归一化项.2018年何等人考虑到相同卷积以及一些其他的翻转等操作得到的特征可以一起进行组归一化(GN)[15]，故将网络中每个样本的feature map的通道(channel)分成G组，每组将有Channel/G个通道，对这些通道中的元素求均值和标准差，这样各组的通道用其对应的归一化参数独立地进行归一化，进一步提升了小Batchsize上的训练效果.GN与BN和LN的区别如图2所示，N作为batch轴，C作为通道轴，(H×W)作为空间轴.

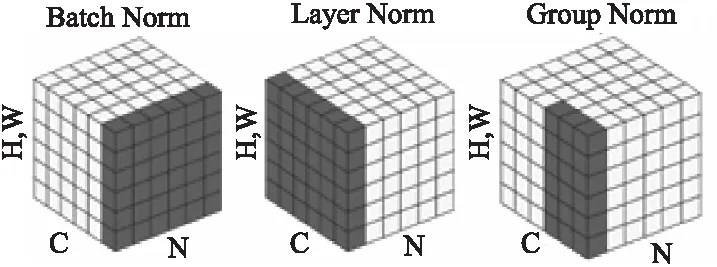
图2 3种归一化方法

受启发于Batch Normalization，2016年Salimans等人提出了Weight Normalization(WN)[18]从权重的角度来提升网络的泛化能力.2018年黄雷等人提出了Orthogonal Weight Normalization(OWN)[19]，此方法将权重正交降低了权重的冗余，并且验证了和BN相结合提升了网络学习能力.2019年CVPR，SiyuanQiao等人提出了Weight Standardization[20]，此方法与GN将结合，得到了在小batch上可以获得比大batch上BN更强的性能.

3 去相关层归一化

3.1 白化(Whitening)

在CNN中，数据集X∈RN×HWC具有4个维度.其中，N表示输入样本的个数，H和W代表样本的高和宽，C是X的通道数，并且扰动变量ε>0是为了数值稳定，防止根号下为0.传统的层归一化的均值和方差设计如下：

(1)

(2)

Xn代表了数据集中的某个样本，公式(1)和公式(2)可以使得数据不同通道的特征具有相同的均值和方差.但是传统的层归一化并没有对数据特征进行去相关的处理.一种直观的解决方案便是白化，标准的白化过程φ：RN×HWC→RN×HWC定义如下：

φ(X)=Σ-1/2(X-μ·1T)

(3)

(4)

(5)

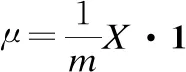
为了能够解决“随机轴变换问题”，一种直接的解决方案通过一个旋转矩阵D将PCA白化后的数据变换到原来的坐标轴下，这便是ZCA白化：

Σ-1/2ZCA=DΛ-1/2DT

(6)

大量研究表明[17，19]，ZCA白化可最大程度地减少欧式距离下由白化引起的失真.因此，去相关层归一化的表达式为：

DLN(X)=DΛ-1/2DT(X-μ·1T)

(7)

3.2 反向传播(Back-propagation)

关于ZCA白化的反向传播对于网络的学习及其重要，这里通过[21]给出了ZCA白化的反向传播公式：

(8)

(9)

(10)

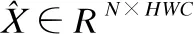
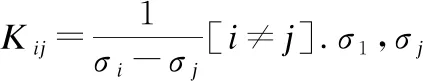
(11)

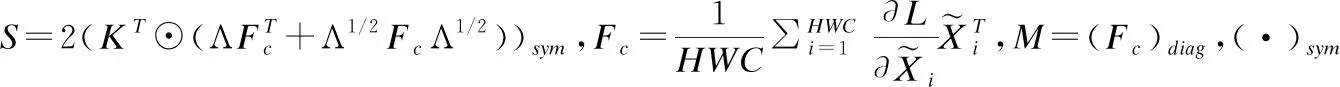
3.3 复杂度分析

本节我们主要分析对卷积神经网络应用归一化算法的复杂度.以BN为例，我们以对于传统的卷积神经网络来说有BN(conv(Wx))，其中样本X∈RM×H×W×C，权重W∈RC×N×Fh×Fw，conv(Wx)∈RM×H×W×N.其中M代表批次大小，C为通道数.Fh×Fw分别代表滤波器的高度和宽度.计算复杂度时，我们将根号计算和加减法的复杂度去除，设维度为M×H的矩阵与维度H×N的矩阵相乘的复杂度为θ(MHN).则对于BN的神经网络有输入conv(Wx)∈RM×H×W×N.BN的算法如下：

(12)

(13)

(14)

(15)

conv(Wx)的复杂度是θ(MNHWCFhFw).

第1步.乘法0次；

第2步.乘法MHWC次；

第3步.乘法MHWC次；

第4步：乘法MHWC次.因此BN的操作复杂度为θ(MNHWCFhFw+3MHWC).

同理我们可以得出GN和LN的时间复杂度与BN一致.

针对我们提出的DLN算法，根据公式(5)得到出1步的乘法次数为M2HWC，根据公式(6)计算第2步的乘法次数为M2HWC+(HWC)2M，根据公式(7)计算第3步的乘法次数为M2HWC，结合conv(Wx)的复杂度是θ(MNHWCFhFw).DLN的复杂度为θ(MNHWCFhFw+3M2HWC+(HWC)2M).各种归一化算法复杂度对比如表1所示.

表1 不同的归一化复杂度

3.4 训练

像层归一化一样，去相关层归一化可以广泛的嵌入在各种深度网络结构中.算法1和算法2分别描述了去相关层归一化的前向和反向过程.

算法1.去相关层归一化的前向过程

输入：数据X∈RN×HWC超参ε

1.根据公式(4)和公式(5)计算X的均值μ和协方差矩阵Σ

2.特征值分解 Σ=DΛDT

算法2.去相关层归一化的反向过程

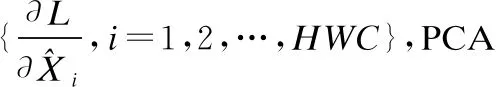
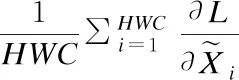
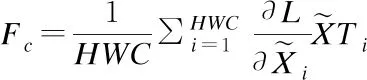
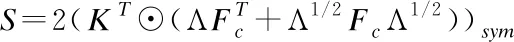
4 实验与分析

实验所使用的去相关层归一化算法及其对比实验均基于Linux(Ubuntu 16.04)下的Python3.6以及PyTorch0.4深度学习框架实现，为了加快训练过程，实验采用 NVIDIA GTX 1080 Ti加速训练.

主要聚焦于图像分类任务来评估去想层层归一化算法的性能，并且在CIFAR-10和CIFAR-100数据集上验证了去相关层归一化的有效性.其中CIFAR-10有10个类别的图像，图像的大小为32×32×3，每个类别有5000个训练样本和1000个测试样本.相较于CIFAR-10，CIFAR-100有100个类别，每个类别有500个训练样本和100个测试样本.将去相关层归一化算法应用在标准的卷积神经网络中来验证本文方法的普适性，包括VGG Network[22]和Wide Residual Network[23].

4.1 VGG Network

首先测试了在VGG-16上的算法性能.实验中我们使用了SGD优化，并且设置了momentum为0.9，weight decay 为0.0005.为了更好的观察拟合效果我们设置了epoch为100，并且分别40，80个epoch后让learning rate×0.1.

4.1.1 对比不同的Batchsize

由于层归一化作用在图像的通道层面，这不依赖Batchsize的大小，因此评估了不同Batchsize={2，4，8，16}的效果.参考GN的设计方案，我们设置Batchsize=16时候的学习率为0.005，由于Batchsize的大小与学习率正相关，设置Batchsize为N的时候的学习率为0.005×N/16，以消除Batchsize大小对学习率的影响.实验结果如图3所示，不同Batchsize在CIFAR-10上的效果，可以看到去相关层归一化对不同的Batchsize影响较小，这也意味着去相关层归一化为小Batchsize的训练提供了新的选择方案.

图3 不同的Batchsize在VGG网络上的效果

4.1.2 对比不同的归一化方法

进一步的我们比较了去相关层归一化和其他归一化方法.图4和图5是分别在CIFAR-10和CIFAR-100上的测试效果，BN是Batch Normalizaiton，GN是Group Normalization，DLN是去相关层归一化方法，其中实线是训练集性能，虚线是测试集性能.图4(a)，图5(a)是3种归一化方法在Batchsize=2时候的表现，显示了DLN在小Batchsize的时候有着更好的泛化能力.图4(a)，图5(b)是3种归一化方法在Batchsize=16时候的表现，DLN虽然在大Batchsize效果不如BN，但是依旧比传统的GN效果更好，在CIFAR-100上DLN只需要训练40多个epoch便可以达到GN相同的性能.最终测试准确率如表2和表3所示，可以看到，本文方法在Batchsize=4和Batchsize=2的时候都具有最好的效果，特别是在CIFAR-100上，相较于BN和GN，DLN分别提升了4.01%和1.97%.

图4 不同归一化算法基于VGG-16网络在CIFAR-10数据集的性能表现

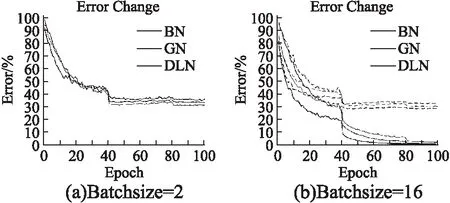
图5 不同归一化算法基于VGG-16网络在CIFAR-100数据集的性能表现

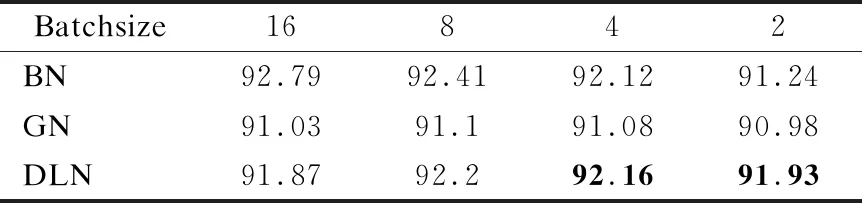
表2 不同的归一化方法在CIFAR-10上的top准确率

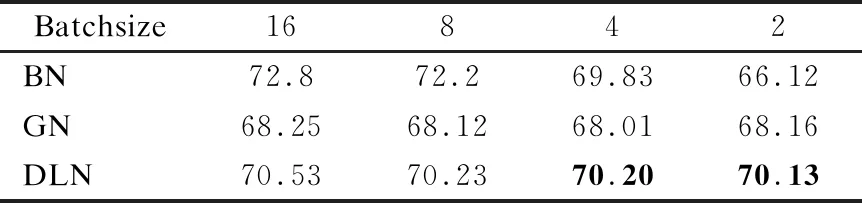
表3 不同的归一化方法在CIFAR-100上的top准确率

4.2 Wide Residual Network

为验证本文方法在大网络中依旧有效，我们将本文算法应用在了 wide residual network，并替换其Normalization层为DLN.在这里使用了PyTorch-Classification(1)http：//github.com/bearpaw/pytorch-classification.代码库中的WRN-28-10-drop基础配置，将其epoch设置为150，并且分别在50，80，110，130 epoch后让learning rate×0.1.另外，我们设置Batchsize=32时候的学习率为0.05，并且设置Batchsize为N的时候的学习率为0.05×N/32，其他设置保持不变.图6和图7分别是WRN网络在CIFAR-10和CIFAR-100上的测试效果，我们可以观察到去相关层归一化在Batchsize=2的时候依旧具有最好的性能，比当前流行的组归一化具有更强的泛化能力，并且稳定性上要好于传统的层归一化算法(LN).最终结果如表4所示，可以看到Batch normalization在小Batchsize时效果不如GN和DLN，由此可以进一步证明BN不适用于小批量数据集.注意到DLN使用小Batchsize在CIFAR-10和CIFAR-100上分别比BN高出了0.8%和1.94%.并且相较于传统的层归一化方法，网络性能得到了进一步的提升，在两个数据集上分别提升了0.75%和1.02%.

表4 不同归一化算法基于Wide Residual Network在CIFAR数据集的top准确率

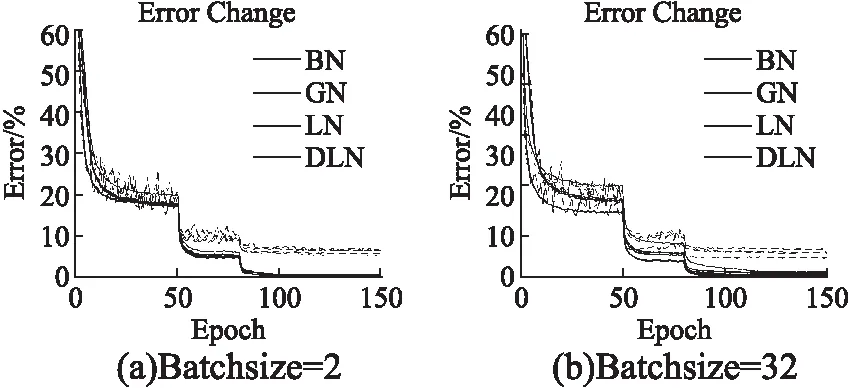
图6 不同归一化算法基于Wide Residual Network在CIFAR-10数据集的性能表现

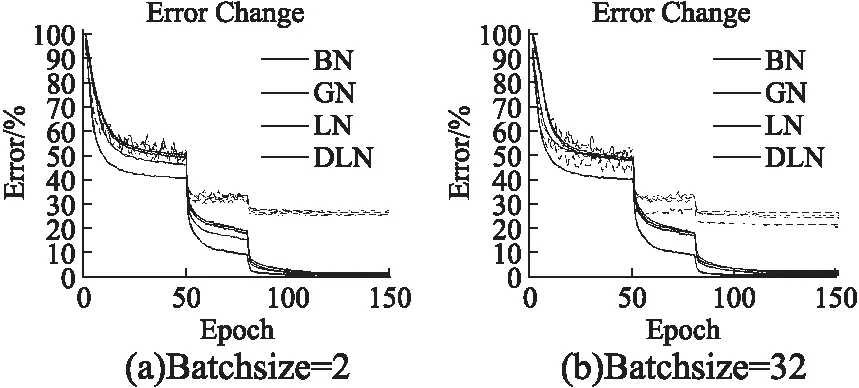
图7 不同归一化算法基于Wide Residual Network在CIFAR-100数据集的性能表现

4.3 算法的效率

我们对比了不同的归一化算法的执行效率，为了多方面的比较执行效率，首先选用[10×10，100×100，1000×1000]多种维度的矩阵进行效率的对比.从表5中，可以看出DLN在样本数，也即第1维度越来越大时，算法的执行效率会跟BN和LN两种算法的差距越来越大.这主要是因为构建的协方差矩阵维度是N×N(第1维×第1维)，SVD分解的时间会随着协方差的复杂度增加而增加.

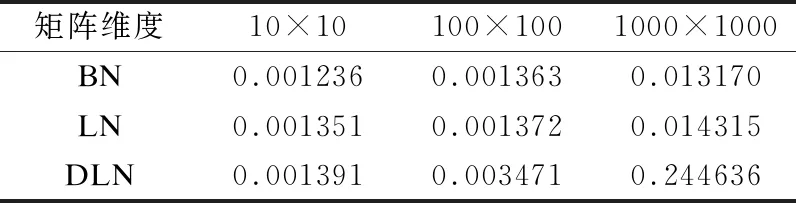
表5 各种归一化算法执行效率(秒) / N×N

在提出的去相关算法的场景下，数据的样本数量应尽可能小，因此进行了进一步的实验，分别对[2×10，2×100，2×1000]这3种维度的矩阵进行了对比，其中我们严格的控制样本的数量为2.表6中可以看出，去相关归一化算法的执行效率与BN和LN的执行效率十分接近.值得注意的是，在2×1000的场景下，达到了0.001419秒的执行效率.并且DLN的准确率在这种情况也是高于LN和BN两种算法的.

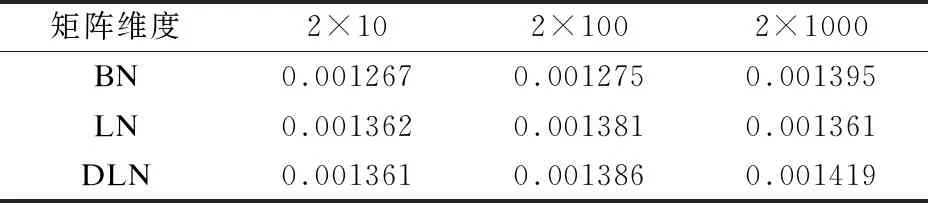
表6 各种归一化算法执行效率(秒) / 2×N

5 总 结

本文提出一种去相关层归一化，该算法通过将ZCA白化加入到传统的层归一化中减少图像通道特征之间的相关性，可以进一步提升层归一化的泛化能力，并且验证了该方法不受Batchsize大小的限制.在CIFAR-10，CIFAR-100数据集上的实验结果证明本论文所提方法与其他归一化方法在小批量样本(Batchsize)训练上表现更加优异，这给小样本训练提供了更好的方案.由于实验聚焦于CNN网络，并没有针对RNN上的任务如文本分类，情感识别等进行验证，将去相关归一化应用在序列模型中并验证其有效性将是我们后续研究工作.