融合Hénon映射和元胞自动机的图像加密算法

陈 祥,张 勇,陈云攀,肖芳艳,刘燕青

(江西财经大学 软件与物联网工程学院,南昌 330013)

1 引 言

伴随着互联网、通信技术和移动摄像设备的发展,数字图像已经广泛地应用于各个领域,并成为人们获取信息的主要方式.但在公共信道上传输的数字图像面临着严重的信息安全问题,传统的文本加密方式无法对数字图像有效加密,专门的数字图像加密技术尤为重要,引起了学术界的广泛关注[1-3].

Hénon映射是一个经典的混沌系统.混沌系统是一种具有优良的伪随机性、初值和参数敏感性及不可预测性的非线性动力系统,它的这些特性十分符合加密系统的需要.自1989年Matthews首次提出并利用一个广义Logistic映射产生伪随机序列用于加密后[4],混沌系统在信息加密方面的研究成为了一个热点,而基于混沌系统的图像加密方法已经成为图像加密研究的主流[5].但单纯地使用混沌系统产生的伪随机序列与明文图像像素异或直接加密图像的方式加密效果不好,容易被差分攻击和已知明文攻击破解.使用混沌系统加密图像时一般会与其他算法结合,采取多轮置乱-扩散的方案将明文图像转化成近似噪声的密文图像.其中,Khan提出构造一个多参数混沌系统,并利用多参数混沌系统的具备的非线性特性设计信道加密S盒,以提高加密系统的加密强度[6];徐亚等提出了基于Arnold映射置乱的方法和多种混沌映射构建新的混沌映射产生混沌序列的双层自适应扩散图像加密算法[7];郭永宁等提出一种将DNA加法、减法和互补映射规则与混沌映射相结合的图像加密方法,使得图像加密算法具有良好的安全性、有效性和鲁棒性[8].

元胞自动机(Cellular Automata,CA)是具有离散时间和离散空间的动力系统,最早由Von Neu-mann和其同事Ulam在研究机器自我复制问题时提出的概念[9].CA因其构造简单、组成单元之间相互作用具有局部性和复杂性、处理并行性、全局复杂性等优点与图像加密中要求的随机性和扩散性符合,适合用于图像加密.Mohamed将图像分块利用可逆一维CA提出了一种并行图像加密算法,该算法可独立加解密每个图像块,加密速度非常快[10];Ping等提出一种基于仿生命游戏的CA规则和混沌的图像加密算法,使用一个2D混沌系统置乱像素位置,再使用仿生CA进行演化达到扩散效果[11];李敬医等基于3D混沌映射和2D二阶可逆CA的图像加密算法,经过多次3D混沌映射对图像进行置乱和2D二阶CA进行混淆的迭代过程完成对图像的加密[12].

在上述研究工作的基础上,本文根据混沌系统和初等元胞自动机的特点,提出了一种新的图像加密算法.该算法利用混沌系统产生伪随机序列,极大地增加了密钥空间大小,增强了加密算法的密钥敏感性;然后根据产生的伪随机序列通过CA演化对图像进行加密,使得加密所需伪随机序列短,图像加密效果好,拥有良好的明文敏感性和密文敏感性,能抵抗各类选择/已知明文等被动攻击.

2 基础理论

2.1 Hénon映射

Hénon映射是Hénon于1976年发现的二维离散混沌系统[13],其解析式如公式(1)所示.

(1)

其中控制参数a=1.4,b=0.3.Hénon映射具有两个Lyapunov指数,分别为0.654和-1.858[14].Hénon映射的相图如图1所示.

图1 Hénon映射相图

Hénon映射作为二维混沌系统要比两个联立但相互独立的一维混沌系统更为复杂.同时由于Hénon混沌系统是离散的,不用求解数值积分的步长且相邻的任何两个状态值间跳跃大,相较于三维Lorenz混沌系统更为简单,计算开销小,易于实现[15].

2.2 元胞自动机

元胞自动机是由元胞、元胞空间、元胞邻居和元胞规则组成的一个动态系统.初等元胞自动机是元胞仅具有两种状态,邻居半径为1(即元胞状态仅受其自身及左右两个邻居元胞影响)的一维系统.图2为周期型边界的初等元胞自动机排列示意图,初等元胞自动机由3个相邻的元胞组成,浅色元胞为深色元胞的邻居元胞;周期型边界指相对边界是连接起来的元胞空间,即对在边界的元胞A来说其左邻居为B,元胞B右邻居为A.

图2 初等元胞自动机元胞空间

CA中每一个元胞状态的更新是由其自身和邻居在前一个时刻的状态所决定的,其局部转换函数可以写成公式(2)形式.

(2)

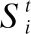
表1 初等元胞自动机75号规则表

初等CA的256种规则中的大部分规则会使得CA演化迅速进入稳定态和周期态,不适合用于隐藏信息,故只选取16种演化后0和1数目均等的具备混沌特性的规则作为加密过程中的演化规则[16].这16种规则记为F={30,45,60,75,86,89,90,101,102,105,135,149,150,153,165,195}.

3 算法设计

加密算法流程如图3所示,由Hénon映射根据密钥K产生6组序列,明文图像P转换为二进制矩阵后,依据这6组序列逐行逐列进行CA演化,利用CA演化比特级地扩散图像信息,迭代3次后,得到密文图像.

图3 加密算法示意图

3.1 伪随机序列

本算法中设图像的大小为M×N,则需要的伪随机序列长度为L=2(M+N).使用的密钥长度为512位,令包含64个8比特字节的密钥为K={k1,k2,…,k64},按照文献[17]中的方式采用逐级迭代法借助Hénon混沌映射产生伪随机序列{aj},j=0,1,2,…,L-1.根据伪随机序列{aj}得到6组序列用于加密,其中{aj}中前M个伪随机数作为行初始演化伪随机序列X;第M+1至M+N个伪随机数作为列初始演化序列Y.将第M+N+1至2M+N位的伪随机数的低4位对应十进制后的值作为规则列表的索引,取得长度为M的行演化规则序列,记作序列V,用于决定每次进行CA演化操作时的规则,而其高4位对应的十进制后的值按照演化步数公式参与演化步数的计算,得到行演化步数序列Sr;余下的第2M+N至2(M+N)个伪随机数进行与得到序列V和序列Sr一样的操作,得到对应的列演化规则序列W和列演化步数序列Sc.

演化步数公式为:

si=2*Max(M,N)+⎣Max(M,N)/8」+ti

(3)

其中M和N分别为图像的高和宽,ti为伪随机序列中第i位伪随机数的高四位对应的十进制的数.

故X和Y是值为0～255的伪随机序列:

X=[x1,x2,…,xM]

(4)

Y=[y1,y2,…,yN]

(5)

V和W是值为16种规则号的规则序列:

V=[v1,v2,…,vM]

(6)

W=[w1,w2,…,wN]

(7)

Sr和Sc是根据公式(3)计算得到的步数序列:

Sr=[rs1,rs2,…,rsM]

(8)

Sc=[cs1,cs2,…,csN]

(9)

3.2 图像加密算法

图像加密过程如下:

Step 1.将明文图像PM×N转化为一个二进制矩阵BM×8N,即将一个M行N列的图像字节矩阵按行将每一个灰度值转化为M行8N列的二进制矩阵.

Step 2.取规则序列V中的第1个值作为CA规则Fv1对序列X进行CA演化,按步数序列Sr中的第一个值rs1,取其演化后的第rs1步与矩阵B的第一行b1按位异或计算得到一个临时序列rl,即rl=Fv1(X)⊕b1.

Step 3.取规则序列V中的第2个值作为CA规则Fv2对序列rl进行CA演化,取其演化后的第rs2步与矩阵B的第2行b2按位异或计算得到新的序列r2,即r2=Fv2(rl)⊕r2,并将r2作为新矩阵R1的第2行.

Step 4.取规则序列V中的第i个值(i==3,4…,M),作为CA规则Fvi,对R1矩阵中的第i-1行进行CA演化,取其演化第rsi步与矩阵B的第i行按位异或计算得到对应的新序列ri,即ri=Fv1(ri-1)⊕bi.

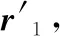
Step 6.将矩阵R1,M×8N转置为R2,N×8M,按步骤Step 2至Step 5行演化的方式,对应地利用伪随机序列Y、规则序列W和步数序列Sc对矩阵R2进行列演化,得到列演化后的矩阵R3,N×8M,并将矩阵R3,N×8M转置为矩阵R4,M×8N,完成一次CA列演化.

Step 7.重复步骤Step 2至Step 6,完成3次行演化和列演化得到密文二进制矩阵DM×8N,将矩阵D重新合成图像字节矩阵CM×N,得到密文图像C.

3.3 图像解密算法

图像解密过程为图像加密过程的逆过程,图像解密步骤如下:

Step 1.将密文图像字节矩阵CM×N进行转置后,再转换为二进制矩阵EN×8M.

Step 2.取规则序列W中第一个值作为CA规则Fw1对矩阵EN×8M的最后一行eN进行CA演化,按步数序列Sc中第1个值cs1,取其演化后的第cs1步后与矩阵E的第1行e1按位异或计算得到序列h1,即h1= Fw1(eN)⨁e1.h1为新矩阵H1的第1行.

Step 3.取规则序列W中的第一个值作为CA规则Fw1对矩阵H1的第1行h1进行CA演化,取其演化的后的第cs1步与伪随机序列Y按位异或计算得到临时序列cl,即cl=Fw1(h1)⨁Y.

Step 4.取规则序列W中的第2个值作为CA规则Fw2对临时序列cl演化,取其演化后的第cs2步与矩阵E中的第2行e2按位异或计算得到序列h2,即h2=Fw2(cl)⨁e2,将h2作为矩阵H1的第2行.

Step 5.取规则序列W中的第j个值(j=3,4，…,N),作为CA规则Fwj对矩阵E的第j-1行进行演化,取其演化后的第csj步与矩阵E的第j行按位异或计算得到对应的新序列hj,即hj=Fw1(ej-1)⨁ej,得到完整的矩阵H1,N×8M,完成一次CA列演化的逆过程.

Step 6.将矩阵H1,N×8M转置为H2,M×8N,按步骤Step 2至Step 5,对应地利用伪随机序列X,规则序列V和步数序列Sr对矩阵H2,M×8N进行CA行演化的逆过程,得到中间矩阵H3,M×8N.

Step 7.将中间矩阵H3,M×8N转置为H4,N×8M,重复步骤Step 2至Step 6,完成3次列演化逆过程和行演化逆过程,最终得到明文二进制矩阵BM×8N,将矩阵B重新合成图像字节矩阵PM×N,得到明文图像P.

4 实验仿真

本文算法在AMD R4800H @2.9GHz CPU和16GB DDR4 @3200MHz内存的硬件环境以及Windows 10 64位家庭版操作系统、Mathematica12.2的软件环境下,对大小256×256的8比特灰度图像进行加解密实验.

不失一般性,实验中使用Mathematica软件自带的随机数生成函数生成一组密钥K={195,88,9,128,164,31,214,138,106,23,36,169,21,188,243,40,175,33,100,20,113,133,144,185,94,254,80,10,223,18,172,198,114,228,116,35,57,20,66,50,42,254,81,53,184,25,174,235,160,74,216,14,34,67,255,157,195,143,247,244,131,20,203,186}分别对Lena、Peppers、All-white、All-black四幅灰度图像加密.加解密效果如图4所示,图4(a)-图4(d)为明文图像,图4(e)-图4(f)为对应的加密后的密文图像,图4(i)-图4(l)为对应的解密后图像.从实验结果上看,图像加密后呈现为无任何可见信息的类随机噪声图像,无规律的纹理,与原图像看不出任何关联,解密后的图像与原图像一致,是清晰无损的,加密和解密的视觉效果良好.

图4 实验仿真结果图

5 性能分析

5.1 图像加解密效率分析

在第4节仿真实验所使用的硬件和软件环境下,分别使用本文算法和文献[18-20]中的算法对大小为256×256的Lena图像进行加解密操作,所用时间如表2所示.

从表2中可以看出,本文提出的算法加解密速度在4种算法中一般,文献[19]加解密速度远快于本文算法以及文献[18,19]的算法.本文加密速度略落后于文献[18]中算法加密速度,解密速度也慢于文献[18]中的算法.但本文算法的加解密速度均略快于文献[20]的算法.

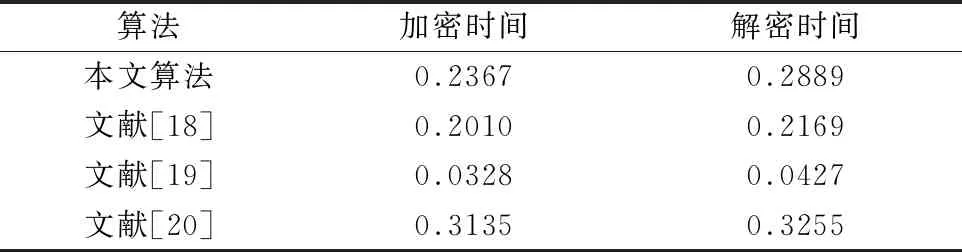
表2 加密和解密效率对比(s)

5.2 密钥空间分析

密钥空间是指一个加密系统所有合法密钥的集合,密钥空间的大小取决于该加密系统合法密钥的长度.密钥空间大小是体现加密系统强度的最重要特性之一,其直接决定着加密算法在遭受暴力破解攻击时的安全性.本文提出的加密算法采用了512位长的密钥,密钥空间大小为2512≈1.34×10154.可见本文提出的加密算法的密钥空间足以抵抗穷举攻击.

5.3 统计分析

通过对加密图像的像素值进行统计分析,找出其中潜在的规律可以破解加密技术.需要对密文图像进行直方图分析和相邻像素相关系数分析,确保加密算法可以抵抗统计攻击[21].

5.3.1 图像灰度值分布统计直方图分析

一个明文图像的像素值分布会具有明显的规律性,攻击者可统计图像所有像素点的像素值的分布频率,获取图像信息,破解加密图像.优秀的加密算法会使得密文图像的像素值分布均匀,与噪声图像分布相似,不具备统计规律.以Lena灰度图为例,图5为Lena明文图像的灰度值分布统计直方图,图6为经本文提出加密算法加密后的密文图像的灰度值分布统计直方图.对比图5和图6可以看出,密文图像灰度值分布统计直方图与明文图像灰度值分布统计直方图差异明显.明文图像灰度值分布具有一定的规律波形,密文图像则很好地去掉了这种统计规律性,使得图像的灰度值分布均匀,不具备可分析性.

图5 明文图像灰度值分布统计直方图

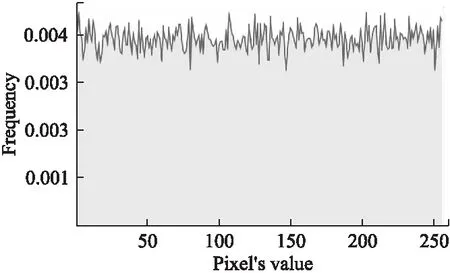
图6 密文图像灰度值分布统计直方图

5.3.2 相邻像素相关性分析

明文图像往往具备较大的信息冗余,像素值相同或相近的像素点会连续出现,相邻像素间相关性强.因此加密效果良好的图像加密算法必须打破明文图像中的像素强相关性,防止攻击者对加密图像中相邻像素进行分析,由其中一个或几个像素点恢复出整个明文图像的轮廓.为分析本文加密算法的去相关性效果,分3次随机抽取明文图像和密文图像中2000对相邻像素点的灰度值,通过公式(10)至公式(13)分别计算图像在水平、垂直和对角3个方向上相邻像素点间的相关性系数.

(10)

(11)

(12)

(13)

其中,xi和yi为图像中两个相邻图像像素点的灰度值,n为随机抽取的相邻像素对数,rxy表示相邻像素点的相关性系数,代表图像的相关性系数.一般情况下,明文图像相邻像素灰度值的相关性接近1,密文图像相邻像素灰度值相关性接近0.

图7中左边3幅图为是Lena明文图像在水平、垂直和对角方向上的相关性相图,右边3幅为其对应方向的密文图像相关性相图.从图7中可以看出,在加密前,相图中相邻像素点灰度值大部分集中在一起,明文图像在3个方向上的相邻像素点呈现明显的正相关性;加密后的密文图像在3个方向上相邻像素点的这种正相关性已消失,相邻像素点的灰度值散乱地铺满整个相图.

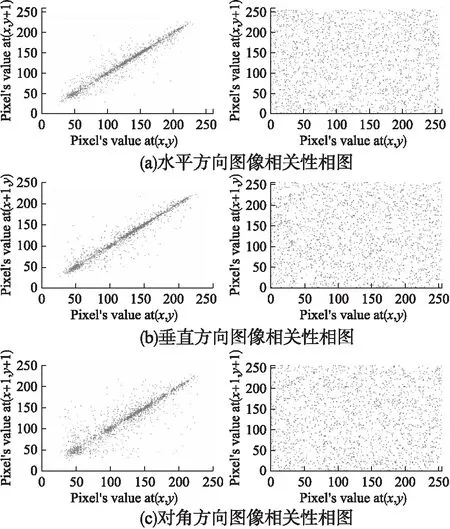
图7 明文图像与密文图像相关性相图

表3列出了Lena明文图像与经本文算法和文献[18-20]的加密算法加密后的密文图像分别在水平、垂直和对角3个方向上的相邻像素灰度值相关性系数计算结果.可以看出,明文图像在3个方向上的相关性系数均在0.9以上,而4种加密算法加密后的密文图像在3个方向上趋近于零相关.说明4种加密算法均能有效打破明文图像相邻像素之间的强相关性.

表3 图像相邻像素相关性系数计算结果

5.4 信息熵分析

信息熵是用于衡量图像所包含有效信息和图像的随机性的重要指标.一般认为,像素值分布随机性越强,信息熵越大,图像所能体现的可视信息越少.信息熵计算公式如下:

(14)

其中,si表示像素值为i的像素点,p(si)表示像素点si的出现概率,n表示图像中所有像素的个数.对于8比特的理想随机灰度图像来说,灰度值为8,信息熵的理论值为8.

表4给出了明文图像(图4(a)-图4(d))和本文算法得到的密文图像(图4(e)-图4(h))以及文献[18-20]加密Lena、Peppers、全黑图像与全白图像等4张图像后密文的信息熵计算结果.可以看出,各个明文图像的信息熵计算结果偏离随机图像的理论值8比特,本文算法与文献[18,19]中的算法加密后的密文信息熵极为接近理论值,略强于文献[20],说明本文算法加密后的密文像素随机性强,不会发生信息泄露.

表4 明文图像和密文图像信息熵结果对比(单位:比特)

5.5 敏感性分析

破解密文图像的一种常用攻击方法为差分攻击,即细微地改变加密过程中密钥、明文或密文,分析改变后的密文与原密文间的联系,达到破解密文图像的目的.加密算法的敏感性决定着该算法抵抗差分攻击的能力.加密算法的敏感性越好,即密钥、明文或密文的细微改变都会造成加密或者解密后图像的巨大差异,将使得攻击者无法分析出修改前后两幅密文间的联系,难以实施差分攻击.衡量两幅图像差异有3个重要的指标,像素改变率(number of pixels change rate,NPCR),在两幅图像同一位置处,用于描述不同像素点个数占全部像素的比例;一致平均变化强度(unified average changing intensity,UACI),用于描述两幅图像相应位置处的像素点间的差值与理论上像素点间的最大差值(即255)的比值的平均值[22];块平均变化强度(block average changing intensity,BACI),用于描述两幅图像的差图像的图像块间任意两个像素差值的平均值与最大差值(即255)的比值[23],其计算方法请参考文献[22,23].

5.5.1 密钥敏感性分析

密钥敏感性比较的是采取不同密钥加密同一个明文图像后密文图像的差异.理想情况下,不同密钥加密同一个明文后的密文为互不相关的随机噪声图像,因此在密钥敏感性中,NPCR和UACI的理论值为两幅随机图像的差异.对于两幅256×256大小的8比特随机图像,NPCR和UACI的理论值分别为255/256≈99.6094%和257/768≈33.4635%,BACI的理论值约为26.7712%.测试中采用的密钥敏感性的分析方法为,随机产生一个密钥,仅细微地改变密钥中的某一位的值,得到另一个密钥,再分别使用这两个密钥对图4a的Lena图像加密,得到两幅密文图像,最后计算这两幅密文图像间的NPCR、UACI和BACI的值.对本文及文献[18-20]中的加密算法进行100组实验取平均值后计算结果如表5所示.

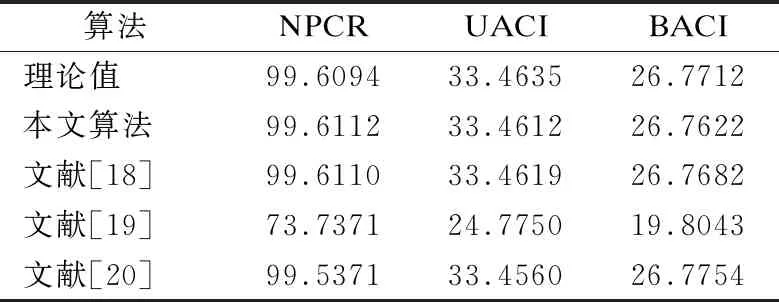
表5 密钥敏感性分析结果(%)

从表5中可以看出,本文与文献[18]中的加密算法密钥敏感性强,测试所得的计算结果均趋于理论值,比文献[20]的算法略强,优于文献[19].说明本文提出的算法具有优秀的密钥敏感性.

5.5.2 明文敏感性分析

明文敏感性比较的是采用相同密钥,加密不同明文后所产生的不同密文图像的差异.理想情况下,不同密钥加密同一个明文后的密文为互不相关的随机噪声图像,因此在明文敏感性分析中,NPCR和UACI的理论值为两幅随机图像的差异.对于两幅256×256大小的8比特随机图像,NPCR和UACI的理论值分别约为99.6094%和33.4635%,BACI的理论值约为26.7712%.测试中采用的明文敏感性的分析方法为:使用同一密钥,对Lena图像和其细微改变的对应的图像(这里随机改变Lena图像的某个像素点的某一位)进行加密,得到两个密文图像,之后计算这两个密文图像的NPCR、UACI和BACI的值,测试100组实验取平均值,列于表6.

表6给出了本文算法与文献[18-20]中算法的明文敏感性分析结果.本文算法的明文敏感性在精度上与文献[18]和文献[19]相当,均优于文献[20],说明本文提出的算法具有优秀的明文敏感性.

表6 明文敏感性分析结果(%)

5.5.3 密文敏感性分析

密文敏感性比较的是使用原密钥对修改后的密文进行解密,所得到的解密图像与明文图像之间的差异.理想情况下,修改后的密文无法使用原密钥解密得出正确的明文图像,解密所得仍是不含任何有效信息的随机的噪声图像.实验中采用的测试图像为标准Lena图像,因此密文敏感性中的NPCR、UACI以及BACI的理论值为Lena图像与随机图像之间的值,分别为99.6094%、28.5923%和21.3268%.

实验中采用的密文敏感性的分析方法为:随机生成一个密钥,对Lena图像进行加密之后,随机改变密文图像中的某一像素值的某一位得到一个新的密文图像,使原密钥对原密文图像和新密文解密分别得到明文图像和一个解密图像,计算该解密图像与正确的明文图像之间的NPCR、UACI和BACI的值.表7给出了本文与文献[18-20]中算法进行100组密文敏感性测试后去平均值的计算结果.从表7中可以看出,本文提出的算法密文敏感性测试的结果与理论值十分接近,密文敏感性要优于文献[18-20]中的算法.说明本文提出的算法具有极佳的密文敏感性.

表7 密文敏感性分析结果(%)

综合图像加解密效率分析、统计分析和敏感性分析,可知本文提出的算法优于文献[18-20]中的图像加密算法.

6 结 语

本文利用Hénon映射和初等元胞自动机的良好特性,提出了一种高效安全且能抵抗差分攻击的图像加密算法.使用逐级迭代Hénon映射产生具有良好统计特性的伪随机序列,解决了仅利用CA规则空间作为密钥而导致密钥空间小的问题;使用CA演化加密,可直接替代传统的置乱-扩散结构进行高效加密,加密效果好,易于实现,丰富了传统意义上的置乱-扩散图像加密技术;加密所需的伪随机序列较短,对于宽为M,高为N的图像只需要2(M+N)长的伪随机序列;依据混沌序列选取元胞自动机规则进行演化使得图像像素灰度值变得随机不可预测,可保证每次演化后加密的有效性.通过仿真实验,对各个加密指标进行了对比测试,结果表明,提出的图像加密算法具有速度良好和加密系统敏感性强的优点.本文算法可应用于网络图像信息安全和区块链图像信息安全分享等方面..