高等数学课程思政实施路径探索与实践

张冠男 李萍

【摘要】《高等数学》是公共必修课，但学生普遍存在畏难心理.同时，为应对疫情，本校创设了“一主体双引擎四驱动”的教学模式，本着润、新、艺、展的原则，在从课程建设到学生评价各环节中，梳理实施路径与方法，以实现课程思政与高等数学的双提升.

【关键词】课程思政;高等数学;思政育人;教学模式;疫情教学创新

《高等数学》是理工科各专业的必修课程，为学习专业基础课及相关专业课程打下必要的数学基础，以及提供必需的数学概念、理论、方法、运算技能和分析问题解决问题的能力素质.

大学生需要思想的引导，需要德行的耳濡目染，需要教师适当的情感熏陶，以帮助其树立社会主义核心价值观，以便以后在社会实践中有所思，并有所为、有所不为.

教师应以“帮助树立正确的人生观、世界观、价值观，培育工匠精神和职业道德”这条意识形态为主线，“以应用为目的，以必需、够用为度”为原则，以“价值引领、隐形施教”为理念，结合工科专业特性，从德育和职业素养两方面，梳理出思政元素：从“课程思政”入手，围绕课程体系建设标准，常规课程育人和第二课堂育人三个环节进行课程思政建设，在教学中渗透数学所蕴含的科学精神、人文精神、数学文化，以努力提高学生的数学修养和素质，让思政元素贯串育人全过程，努力实现政治认同、思想认同、情感认同、价值认同.

一、教学模式

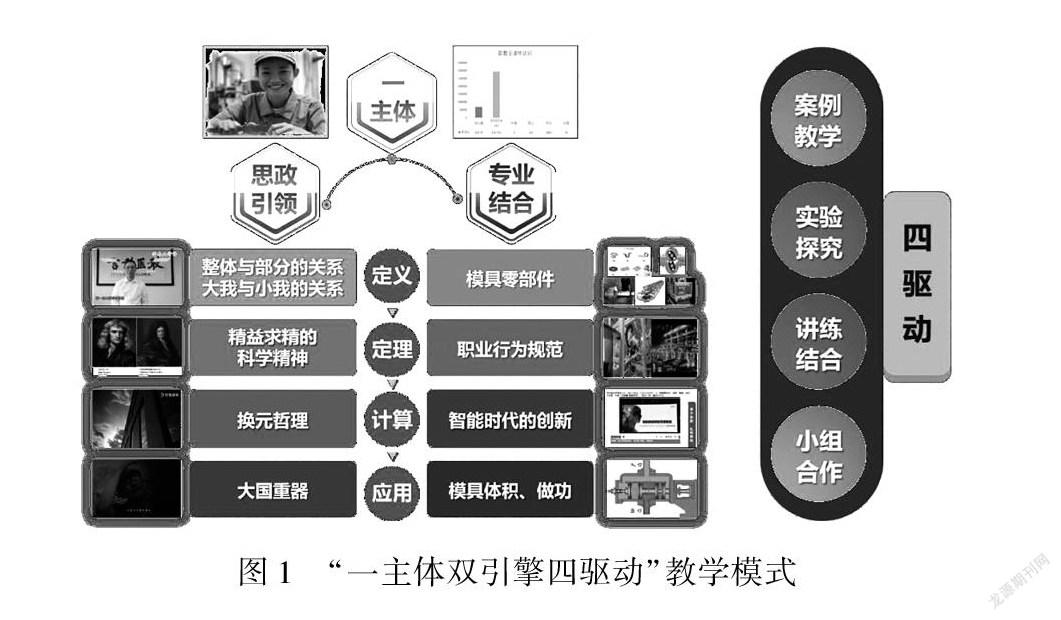
教师应采用“一主体双引擎四驱动”的教学模式，在教学过程中注重“导、思、探、练”的结合，融合课程思政，转变学习方式，以第二课堂拓展教学空间，开展线上线下混合式教学;以基本概念为基础，以实际应用为目的，以必须、够用为原则，灵活运用启发式、讨论式、研究式等教学方法组织教学活动.面对疫情给高职教育带来的极大挑战，教师应采用腾讯课堂与面授相结合的方式，以云课堂辅助进行相关教学活动，不断修订教学策略.教学实施过程分为课前、课中和课后三个阶段，教师应在课中融入头脑风暴、讨论、小组PK等课堂互动，强化过程性考核和科学评价，将信息化技术与教学策略有机融合.

通过教学实践创立的“一主体（学生）、双引擎（思政引领、专业结合）、四驱动（案例教学、实验探究、讲练结合、小组合作）”教学模式，将实例与教学内容有机结合起来，既增强了学生数学实际应用能力，又加强了大国工匠精神的德育培养.学生通过“四驱动”的能动作用，掌握了推理、归纳、总结等思想方法，获得了应用数学的能力，以及创新意识和主动探索学习的精神.

一主体：以学生为主体，尊重学生的认知规律，激活参与主体，建构知识体系，提升综合能力.

双引擎：构建思政引领和专业结合双引擎.课程思政与教学内容相辅相成，实现思政要素全方位育人要求;教学内容与专业相结合，在课堂中融入专业要素，真正服务于专业.

四驱动：指案例教学、实验探究、讲练结合、小组合作四种教学方法.

二、課堂组织

疫情期间，开展腾讯课堂与智慧教室相结合的线上线下混合式教学，通过云课堂和腾讯课堂进行师生、生生交流互动，保障线上线下学生的全员覆盖.搭建丰富的云课堂教学资源，通过云课堂发布课前、课中和课后任务，构建全链条知识结构，为学生提供完善的线上教学场景和教学资源;采用腾讯课堂直播讲解，运用举手连麦、投票、讨论区回答等多种线上互动形式，针对学生参与的活动量化打分，融入职教云评价体系，提高学生的参与度和积极性;通过QQ群发布课堂计划、答疑，及时与学生沟通，督促学生学习，奖励先进生，帮扶后进生，提高学生参与度.

对学生个体的关注.首先体现在承认每个学生的独特性，及时对学生的努力、进步提出肯定和鼓励.其次，每周汇总上周学生学习进度、测验题目、优秀作业等，及时跟进学生学习进度.然后，采用QQ群、微信和线下等方式不定时、不定点回答学生问题，偏远地区网络不好的学生可进行电话解答，共性问题及时总结发布.最后，将优秀作业、学习进度、学生视频，以及祝福综合到一起，制作班级结课视频.

动静结合，应用数字化资源丰富课堂.用MATLAB绘制二维、三维动画，并演示定积分的求解过程.计算机模拟演示，使学生在获得直观视觉冲击的同时，为掌握理性知识创造条件.在学习数列的极限时，教师可以引导学生在数学软件上取点绘图，利用软件的动态变化优势，观察数列连续变化情况;在讲解微积分的应用时，教师可以引入数学模型，注重实际问题的解决，强实践、重应用，培养学生的实践动手能力、知识的应用能力.

建构丰富多彩的第二课堂，鼓励学生积极参与其中.如数学建模比赛、趣味数学竞赛、数学文化节等活动，在活动中潜移默化地接受思政教育.

注重教师评价、学生互评，并引入专家机制，将学生对微积分的认识提升到对微元思想的掌握，并上升到价值观的理解.学生的最终总评成绩应将思政元素作为评分要素，教师应在学生平时的学习过程中，根据其体现出来的政治素养进行考核评价.同时，加入学生评价课程思政的融入效果，最终形成立体式评价体系.

三、融入原则

借助抽象的数学符号，拉长人生的深度和长度.用典故引发共鸣;用热点触动情感;用哲学启发思考;用精神激发活力.

教师在教学过程中应用哲理思想，可加深学生对数理概念的理解与掌握;通过概念定理的解析，辅助学生掌握一定的哲理思想;拓展相关哲理思想，提高学生的思辨和逻辑推理能力.教师要结合现实生活实际和专业知识，创设教学情境;组织辩论PK，在团队合作的同时，融入合理竞争，可以更好地培养学生的团结协作意识，提高其人际关系管理能力.

（1） “润”——潜移默化

思政与课程相辅相成，互为依托，两方共同促进学生的理解;思政融入点，要契合课程进度要求.

（2） “新”——与时俱进

新内容：紧跟时代潮流要求，注意更新.同时，为了吸引学生的注意力和兴趣，可以加入当代热点.

新形式：利用交互媒体，了解学生需求，加强与学生之间的互动，以学生讲解思政案例、思政视频及文案创作等方式，将思政教育内容与课堂知识融为一体.

（3） “艺”——艺术美感

重新审视教学过程，把整个教学过程看成以书本知识为基础来进行合理拓展的过程.思政元素可大可小，但是切入的时间和内容要切合课程进度要求.

（4） “展”——推广拓展

思政元素的融合不能停留在表面，要讲深度、抓细节，提升高度.同时鼓励创新，先行先试，大胆探索，扎实推进.随着互联网不断发展，教师可尝试将各种新媒体运用到教学过程中，将思政教育融入专业课程教学，思政教育就不再是单一知识结构，而将随着多元化的教学方法和手段，融入知识中.

四、融合因素

（1）科学精神——刻苦钻研，严谨笃学，勇于创新

高等数学具有“高度的抽象性、严密的逻辑性和广泛的应用性”的特点，故在概念理解，定理推导，公式验算中，都需要学生具有踏实勤勉的学习态度，这也有助于培养学生良好的学习习惯、数学素养、优良的道德品质、坚强的意志品格，使其形成严谨的思维和求实的作风，以及勇于探索、敢于创新的思想意识和良好的团队合作精神.教师在教学过程中应将努力奋斗、坚忍不拔的拼搏进取精神，以及“中国梦”、爱国主义情感、民族品牌、中国制造等元素，“润物细无声”般地穿插在各章节知识点中，以提升学生的探究精神.

（2）数学文化——逻辑推理，辩证思维，哲理感悟

教师可通过数学概念的学习来引导和教育学生学会做人做事，充分利用好数学这块哲理阵地，挖掘丰富的思政元素，加强学生的思想政治教育.例如，通过极限概念的学习使学生认识到极限思想的本质是马克思主义哲学原理的量变、质变规律，从而培养学生的抽象思维能力和哲学思想的运用能力.从学生的终身发展角度来看，高职数学不应只是学生学习专业课程的工具，更应是培育学生科学素养和综合素质的重要载体.对高职学生而言，在今后的工作中可能会用到的具体的数学知识不多，但是运用数学思维分析解决问题的方法，以及逻辑推理的能力会使他们所从事的工作合理地被量化、简化.

（3）人文精神——孜孜不倦，精益求精，爱国情怀

教师可通过介绍我国古代数学家的成果和事迹，激励学生的民族自豪感和责任感;通过介绍当代企业家与工程师等优秀事迹，增强大学生的民族凝聚力和爱国主义情感;用数学家的成功经历鼓励和鞭笞学生努力学习，立志成才.

（4）担当精神——责任意识，不懈努力，砥砺奋进

教师可通过本课程的学习使学生认识到数学源于实践又服务于实践，紧贴时代脉搏，以培养学生超前思维，让学生明确少年强则中国强，少年肩负着时代重任，要永远跟党走，敢于担当，甘于奉献，要笃实，扎扎实实干事，踏踏实实做人，牢记“空谈误国、实干兴邦”的事实真理，苦干实干.

五、融合模式

教师可采用多种信息化手段，培养学生应用数学意识、创新意识，引导学生学会联想、归纳、总结等思想方法.思政元素融入的形式多样，可逐渐渗透对学生主动探索学习精神的培养.

（1）文化导入型——导数的概念

【實例】由繁体字“導”，讨论“导”的内涵，推出导数的导向驱动作用，进而理解国家主体的导向作用，党的领导意义.

（2）热点带入型——开学第一课

面对疫情，学生能冷静面对，展示了其更加成熟的面貌，以及他们的家国情怀与担当精神.

【实例】开学第一课，提问学生：面对来势凶猛的疫情，祖国各地都在无私奉献，你的家乡都有哪些感人的事件呢？又有多少人冲锋在前，为我们保驾护航，我们身在后方，又能做些什么？

学生之间讨论家乡在疫情中的贡献，和对战胜疫情的信心，总结如下：珍惜生命，敬畏自然;国家有难，匹夫有责;追逐光阴，不负韶光.

【实例】通过对数据图像观察与计算演练，结合导数的性质，了解1月份，2月份疫情增长的凹凸性，预测疫情的拐点，学生纷纷表示有信心，但仍会继续做好防护工作.

题目：模拟流行病学数学模型，计算疫情传播数值，理解我国政府采取严密的防控防治的先见性与必要性.据研究者估计，新病毒传染能力的R0值（基本传染数）为3.77，平均5天的潜伏期和7天的感染期.假设未采取防护措施，1名病毒携带者在5天内将病毒传播3人，那么到某天为止，大概会有100万人染上这种病毒.

（3）情境渐入型——空间曲面方程

【实例】将世界代表性建筑、天津特色建筑共同展示，让枯燥的图像带上色彩，让学生深刻理解空间曲面结构，及对天津建设的自豪感，加深对几何图形的深刻理解.

（4）日期引入型——微元思想

【实例】借助3月14日国际数学节，对圆周率π的重要公式、实际应用、计算简史等做出简略介绍，由此引发学生思考：对于π的计算为何还未停止.

（5）拓展深入型——立体解析几何

【实例】四维空间——独立思考，探索未知.从二维平面解析几何到三维立体解析几何，曲线平面等性质与方程发生了变化，由此推理猜想四维空间.

（6）哲理融入型——梯度思想

【实例】将梯度的局部最优思想，引申为人生没有最优解，号召学生：唯有做好当下，攀登此时此刻的高峰，研读每一个定理，深挖每一个概念，掌握每一门学科，才能达到人生最优的近似值！

六、结语

通过一年的教学实践，我们看到：热点问题，让冰冷的数学符号“暖”起来;哲学素养，让恒定的定理公理“活”起来;专业结合，让枯燥的计算推演“燃”起来;加入辩论、参观、竞赛、角色扮演等多种形式的课堂活动，让被动的课堂讲解“忙”起来;数学文化，让死板的进度计划“亮”起来;资源建设，让传统课堂“动”起来.

【参考文献】

[1]李倩瑶.应用型高校经济数学“课程思政”教学改革的思考[J].科技风，2019（25）：82.

[2]韩曙.高职数学课程融入“课程思政”教育的路径分析[J].花炮科技与市场，2020（02）：126.

[3]胡苗忠.基于“一个引领、一条主线、三个平台”的课程思政框架体系研究与实践：以浙江农业商贸职业学院高职会计专业为例[J].商业会计，2018（14）：127-129.

[4]王和平.国家职业教育改革形势下高职院校立德树人实施路径[J].科教文汇（中旬刊），2019（11）：103-104+114.