济阳坳陷页岩油储层矿物组分最优化反演方法
2022-05-09赖富强李仕超刘粤蛟钟路路黄兆辉王海涛
赖富强,李仕超,王 敏,刘粤蛟,钟路路,黄兆辉,王海涛
(1.宜宾学院,四川 宜宾 644007;2.重庆科技学院复杂油田勘探开发重庆市重点实验室,重庆 401331;3.中国石化胜利油田分公司,山东 东营 257000)
0 引 言
页岩油储层评价的基础在于对页岩矿物组分的准确识别[1-2]。泥页岩的矿物成分对页岩油储层生烃能力和储层的可压裂改造性起到很重要的控制作用[3-6]。烃源岩的矿物成分是判断优质页岩油藏烃源岩能否形成具有经济价值的重要指标,而页岩油储层的矿物组分多样,岩性复杂多变,如何有效地识别出页岩油储层的矿物组分是页岩油勘探开发的难点之一[7-8]。
目前最直观、准确的矿物组分识别方法是直接利用钻井取心[9]和实验分析进行矿物组分识别[10],但由于该方法成本太高,无法对全井段进行连续识别,且岩心取出后易风化变质,难以真实反映井下高温高压环境下的矿物组分[11],不具有现实意义。此外,利用常规测井资料进行矿物组分识别,虽然测井成本较低,并且能够实现全井段的连续识别和评价,具有较强的实用性[12],但该方法依然依赖于实验室岩心测试矿物含量来构建模型[10],模型的准确性和适用性取决于区域内岩心实验数据的数量[13],此外,页岩油储层矿物组分复杂多样、岩石物理体积模型不统一,跨区域很难推广使用[14-18]。
针对上述方法存在的问题,为更加准确定量评价页岩矿物组分含量,此次研究引入有机骨架,构建统一的页岩油储层“双骨架”矿物组分岩石物理体积模型,采用基于岩石物理实验约束的多矿物体积模型最小二乘法-奇异值分解[19]最优化反演方法,准确计算页岩油储层有机骨架和无机骨架矿物组分体积含量,提高识别精度和区域适用性,建立一套高精度、跨区域使用的页岩油储层多矿物反演方法。
1 区域地质概况
济阳坳陷地处渤海湾盆地东南部,被逞宁隆起和鲁西隆起所挟持,展布形态呈一个向西收敛、向东散开的近东西走向的一级负向构造单元[20],是典型的“北断南超”箕状断陷盆地。坳陷内部包含惠民、沾化、东营、车镇四大凹陷及多个凸起。古近纪与新近纪的断、坳转换期以及新构造运动导致坳陷内中浅层断裂密布,为油藏的形成提供了良好的地质条件[21](图1)。
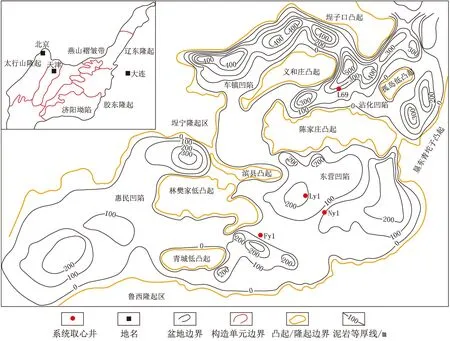
图1 济阳坳陷构造及取心井位置Fig.1 The structure of Jiyang Depression and location of coring wells
研究区古近系由下至上依次发育孔店组、沙河街组、东营组地层,此次研究目标层主要为沙河街组沙三下亚段的沙三下1、沙三下2、沙三下3、沙三下4和沙四上亚段纯上1、纯上2这6个小层。沙三段下亚段岩性主要为纹层状构造的页岩、油页岩、泥岩与具块状层理泥岩形成的不等厚互层,沙四上亚段以纹层状构造泥质灰岩为主,属半深湖—深湖相沉积。
2 页岩油储层矿物特征分析
通过对目的层758块岩样的X衍射全岩矿物室内实验分析可知,济阳坳陷页岩油储层主要矿物类型为碳酸盐岩、黏土矿物、石英、长石、黄铁矿等,碳酸盐岩矿物含量一般大于45%,石英等碎屑矿物含量一般小于30%(图2a)。由矿物组分三角图可以看出(图2b),济阳坳陷的东营凹陷矿物组分较为复杂,且矿物含量与埋深及层位关系不明显;沾化凹陷沙三下—沙四上泥页岩碳酸盐岩矿物含量较东营凹陷大,且随着埋深增大,碳酸盐岩矿物增加趋势明显。
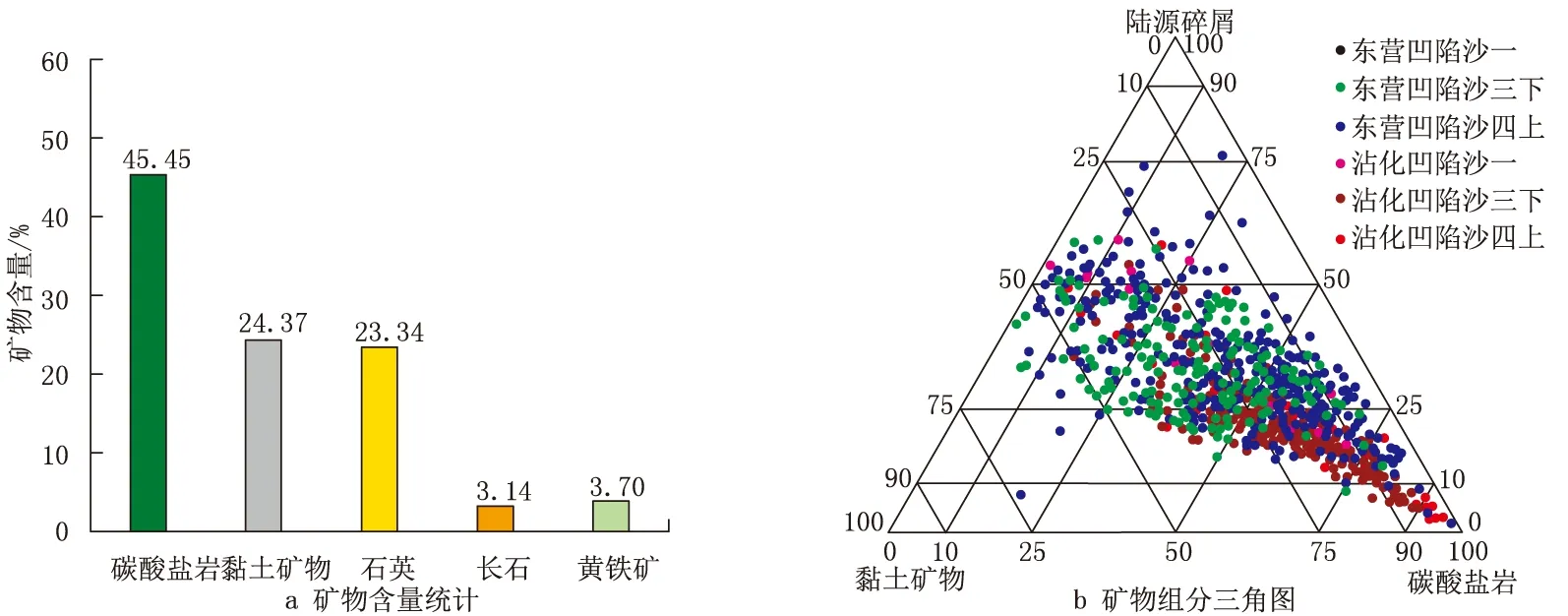
图2 济阳坳陷X衍射全岩矿物岩心分析矿物组分统计Fig.2 The mineral composition statistics of core analysis by X-ray diffraction on all minerals in the rock in Jiyang Depression
3 页岩油储层矿物含量计算方法及模型
页岩油储层矿物组分模型构建及反演方法研究思路:首先根据岩心实验确定主要矿物组分类型及含量范围,然后构建“双骨架”矿物组分体积含量模型,再分别对有机骨架和无机骨架体积含量进行计算。有机骨架计算采用铀和密度交会法计算有机碳(TOC)含量,再基于密度测井计算干酪根体积含量。无机骨架计算首先利用无铀伽马或自然伽马曲线计算泥质含量,然后利用计算得到的泥质含量、干酪根含量对三孔隙度曲线进行泥质校正和干酪根校正,再基于校正后的三孔隙度曲线,采用基于岩石物理实验约束的最优化反演方法计算石英、长石、方解石、白云石等矿物体积含量和孔隙度的含量,最终实现页岩油储层“双骨架”矿物组分体积含量的精确计算。该方法具体实现路径见图3。

图3 页岩油储层“双骨架”矿物模型反演流程Fig.3 The inversion process of "dual-framework" mineral model for shale oil reservoirs
3.1 页岩油储层矿物组分岩石物理体积模型构建
根据岩心实验所获得的矿物组分资料,假设干酪根为有机骨架,结合泥质(黏土)、无机骨架(包含斜长石、石英、方解石、白云石和黄铁矿)、孔隙度等组分,构建集有机骨架和无机骨架为一体的“双骨架”页岩油储层矿物组分岩石物理体积模型(图4)。

图4 页岩油储层矿物组分体积模型Fig.4 The volume model of mineral components in shale oil reservoir
3.2 泥质与有机骨架干酪根体积含量计算方法
3.2.1 页岩油储层泥质含量计算方法
由于干酪根的存在会使铀元素(U)含量升高,导致总自然伽马值(GR)升高,因此,总GR难以反映真实的泥质含量,故利用无铀伽马(KTH)计算泥质含量:
(1)
(2)
式中:GCUR为无量纲经验系数,对第三纪地层为3.7,对老地层为2.0,也可以由实际资料统计获得;KTHmin为纯砂岩段无铀伽马测井值,API;KTHmax为纯泥岩段无铀伽马测井值,API;SH为无量纲泥质指数;Vsh为泥质含量,%。
3.2.2 有机骨架干酪根体积含量计算方法
(1)有机碳含量Gtoc计算方法。考虑有机质丰度变化会引起密度测井变化,故在传统的声波电阻率重叠法基础上加入密度测井的响应特征,Gtoc可表示为:
Gtoc=[A+B·lgR+CΔ]/ρ
(3)
式中:Gtoc为有机碳含量,g/g;R为深侧向电阻率,Ω·m;Δ为声波时差,μs/m;ρ为密度测井,g/cm3;A、B、C为无量纲拟合系数。
(2)有机骨架干酪根体积计算模型。根据密度测井原理,假设密度测井ρ主要测量无机矿物骨架的密度值,Gtoc也可表示为:
(4)
式中:ρtoc为有机碳的密度,g/cm3;Vtoc为有机骨架干酪根体积百分比,%。
根据上式推导可得:
(5)
由于受到井眼环境以及含油性的一些影响导致测井值偏低,或黄铁矿的影响导致测井值偏高,需要对其进行适当的校正,因此,干酪根的体积可表达为:
(6)
式中:Vkero为干酪根的体积百分比,%;λ为无量纲校正因子,对于Vtoc偏低的情形,λ为1.0~2.0,对于Vtoc偏高的情况,λ为0.5~1.0。
3.3 页岩油储层三孔隙度校正
利用前文得到的泥质含量及干酪根含量对三孔隙度测井值(声波时差、补偿中子、补偿密度)进行泥质校正和有机质骨架校正,具体公式如下:
Xm=Xlog-XshVsh-XkeroVkero
(7)
式中:Xlog为三孔隙度测井中的某一测井值;Xm为Xlog校正后的测井值;Xsh为泥质对应的三孔隙度测井值;Xkero为干酪根对应的三孔隙度测井值。
3.4 基于岩石物理实验约束的无机骨架模型最优化反演
3.4.1 页岩油储层岩石物理体积模型测井响应
根据前文构建的页岩油储层矿物组分岩石物理体积模型,主要矿物体积百分含量包括泥质(Vsh,%)、石英长石砂岩(Vqfm,%)、碳酸盐岩(Vcar,%)、黄铁矿(Vpyr,%)、干酪根(Vkero,%)以及孔隙度(φ,%),则:
Vkero+Vsh+Vqfm+Vcar+Vpyr+φ≈100%
(8)
对于任意一个测井值Xlog,其主要来自于上述6个部分的贡献,则有:
Xlog=XkeroVkero+XshVsh+XqfmVqfm+XcarVcar+XpyrVpyr+Xwφ
(9)
式中:Xqfm、Xcar、Xpyr、Xw分别为石英长石砂岩、碳酸盐岩、黄铁矿、地层水对应的三孔隙测井中的任一测井值。
3.4.2 最优化反演方法及流程
(1)最优化系数矩阵。由式(9)可看出,在确定泥质、石英长石砂岩,碳酸盐岩,黄铁矿、干酪根以及孔隙度的体积百分含量的情况下,在3孔隙度测井信息中挑选2种孔隙度测井信息构建2个方程组即可求出Xqfm,Xcar体积百分比,对于进行三孔隙度测井的情形,则有:
Δ-ΔkeroVkero-ΔshVsh=ΔqfmVqfm+ΔcarVcar+ΔpyrVpyr+Δwφ
(10)
ρ-ρkeroρkero-ρshVsh=ρqfmρqfm+ρcarVcar+ρpyrVpyr+ρwφ
(11)
γ-ΥkeroVkero-ΥshVsh=ΥqfmVqfm+ΥcarVcar+ΥpyrVpyr+Υwφ
(12)
式中:Δkero、Δsh、Δqfm、Δcar、Δpyr、Δw分别为干酪根、泥质、石英长石砂岩、碳酸盐岩、黄铁矿、地层水的声波时差值,μs/m;ρkero、ρsh、ρqfm、ρcar、ρpyr、ρw分别为干酪根、泥质、石英长石砂岩、碳酸盐岩、黄铁矿、地层水的密度值,g/cm3;Υkero、Υsh、Υqfm、Υcar、Υpyr、Υw、Υlog分别为干酪根、泥质、石英长石砂岩、碳酸盐岩、黄铁矿、地层水的中子值,P·U。上述各参数均为已知数。
将式(8)代入式(10)~(12)后整理得到最优化系数矩阵式(13)。

(13)
(2)岩石物理实验约束。基于3个方程解2个未知数的问题,属于超定方程,采用约束非负最小二乘法求解,根据地质特征,约束条件为:
(14)
式中:lqfm、Bqfm为研究区目的层段石英长石砂岩最小、最大含量,%;lcar、Bcar为目的层段碳酸盐岩最小、最大含量,%。
根据前述计算模型得到泥质含量、干酪根含量,有:
lcar+lqfm≤Vcar+Vqfm≤100-Vsh-Vkero
(15)
3.5 矿物组分含量计算
联合式(5)、(6)、(7),采用线性约束最小二乘法、奇异值分解等算法对页岩油储层长石石英砂岩、碳酸盐岩矿物组分含量和孔隙度3个未知数进行求解。
3.5.1 方解石、白云石含量计算
利用密度曲线将碳酸盐岩含量分解为方解石和白云石含量:
(16)
Vdol=Vcar(1-Vclc)
(17)
式中:Vclc为分解的方解石百分含量,%;Vdol为分解的白云石百分含量,%;ρdol为白云石密度,g/cm3。
3.5.2 石英、长石含量计算
利用钾元素曲线将石英长石含量分解为石英和长石含量:
(18)
Vfeld=Vqfm(2ks-1)
(19)
Vquaz=Vqfm(2-2Ksh)
(20)
式中:ks为无量纲长石含量指数;Vfeld为分解的长石含量,%;Vquaz为分解的石英含量,%;K为自然伽马能谱测井钾元素测井值,API;Kmtx为无机骨架中的钾元素测井对应值,API;Kfeld为钾长石中的钾元素测井值,API;Kquaz为石英中的钾元素测井值,API;Ksh为泥质中的钾元素测井值,API。
4 应用及分析
根据济阳坳陷页岩油岩心实验确定页岩油储层主要矿物组分类型及含量范围,构建页岩油储层“双骨架”矿物组分体积含量模型,采用文中最优化反演方法对有机骨架和无机骨架矿物组分进行计算,得到FY1井和NY1井矿物组分含量最优化反演成果,如图5、6所示。图5、6中,黑色杆状图为岩心X衍射实验实测的矿物组分百分含量,红色实线为该文最优化反演方法计算的矿物组分百分含量。由图5、6可以看出,“双骨架”矿物组分模型最优化反演计算的矿物组分百分含量与岩心X衍射实验实测的矿物组分百分含量有较高的契合度。表1为FY1与NY1井矿物计算含量与实验含量误差分析。由表1也可以看出,反演计算的矿物组分百分含量与岩心X衍射实验实测的矿物组分百分含量的相关系数均在0.60以上,两者平均相对误差均小于20.00%,说明了模型的合理性。
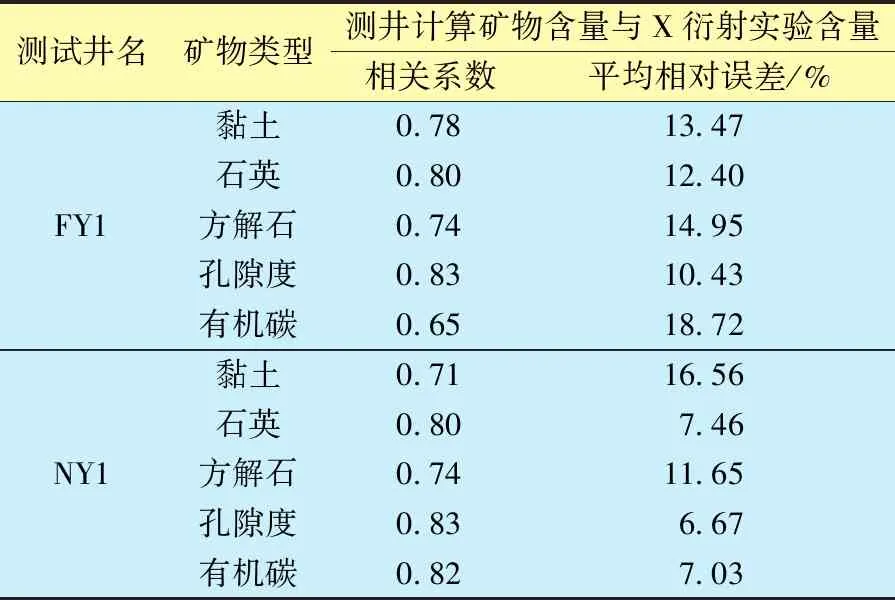
表1 FY1与NY1井矿物计算含量与实验含量误差分析Table 1 The analysis of deviation between calculated content and experimental content of minerals in Wells FY1 and NY1
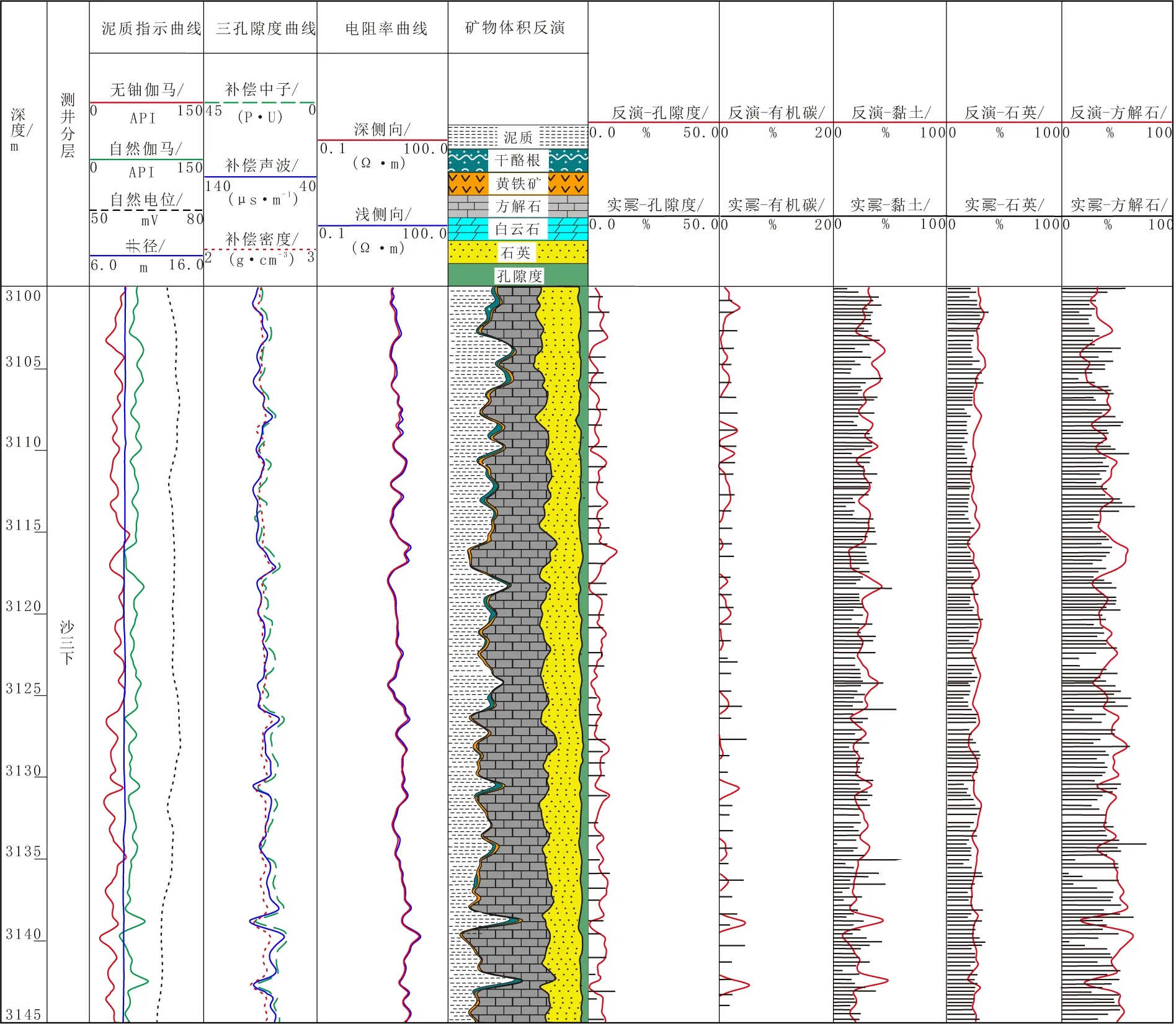
图5 FY1井页岩油井矿物组分识别对比Fig.5 The identification and comparison of mineral components of shale oil in Well FY1
5 结 论
(1)针对研究区岩心X衍射全岩分析等实验而构建的页岩油储层“双骨架”矿物组分岩石物理体积模型,具有较好的区域适用性。
(2)构建的页岩油储层“双骨架”矿物组分模型,通过最优化反演方法计算出来的页岩油储层矿物组分含量与X衍射实验结果的相关系数均在0.60以上,平均相对误差均小于20.00%,取得较好的一致性,验证了该方法的准确性。
(3)该套方法相比一般测井模型来说,优势在于不用依赖于大量的岩心实验,可以根据常规的测井曲线快速获取一些储层物性参数及岩石矿物含量,研究实例结果显示其具有较好的准确率及适用性,便于在页岩油气储层评价中推广使用,可以为页岩油储层定量评价提供一定的技术支撑。

图6 NY1井页岩油井矿物组分识别对比Fig.6 The identification and comparison of mineral components of shale oil in Well NY1
