平台运动对漂浮式风电机组气动功率和推力的影响研究*
2022-05-09白雪峰王晓东赵庆旭潘其云戴丽萍叶昭良
白雪峰 王晓东* 赵庆旭 潘其云 戴丽萍 叶昭良
(1.华北电力大学电站能量传递转化与系统教育部重点实验室;2.华能集团清洁技术研究院有限公司)
0 引言
随着风电行业的高速发展,海上风电尤其是漂浮式风电正成为风电发展的重要方向。相比于陆上风电机组,海上风资源丰富,风剪切和湍流度却很小,可以应用更大容量的机组。另外,漂浮式风电机组在运行过程中下会产生多自由度运动,包括纵荡、横荡、垂荡三种平动以及纵摇、横摇、艏摇三种旋转运动。因此研究多自由度下漂浮式风电机组的气动特性具有现实意义。
国内外学者对整个漂浮式风力发电机组的动态建模和载荷分析进行了大量的研究。美国国家能源实验室针对水平轴3 叶片或2 叶片风电机组气动载荷及结构响应计算开发了一款开源软件FAST。Jonkman[1]等人在FAST程序的基础上开发了水动力学模块HydroDyn,建立了漂浮式风力机“气动-水动-控制-结构”完全耦合计算模型。De Vaal等[2]基于BEM方法将漂浮式机组与固定式机组做了对比研究,发现浮式平台比固定式平台有着更大的运动振幅与频率,并且研究了规定的平台纵荡运动对风电机组的气动性能与诱导速度的变化规律,结果表明:典型的平台纵荡运动不会对风电机组的气动性能产生显著影响。Sebastian 等[3-5]开发了基于自由涡尾迹法的软件WInDS,用于研究漂浮式风电机组的非定常气动性能。研究表明:平台运动会导致机组进入湍流尾流和涡环状态,漂浮式风电机组较陆上风电机组的气动特性更具有非定常性,且目前的BEM方法对多自由度耦合的复杂平台运动不能进行准确的模拟分析。沈昕[6]等人基于升力线的自由涡尾迹方法研究了NREL 5 MW漂浮式风电机组在规定的浮式平台运动下的气动性能。研究表明:在某些平台纵摇、纵荡运动下,与稳态条件下相比,风电机组可以提供更多的空气动力输出。Wen[7-8]等也利用自由涡尾迹法分别研究了平台纵荡运动对风电机组总体性能的影响,推导了功率和推力曲线与叶尖速比、平台运动频率和振幅的函数关系。其研究发现,随着平台运动的振幅和频率的增加,在低叶尖速比时,平均功率输出减小,而在高叶尖速比时,平均功率输出增大;平均推力在任意尖速比下都与平台运动的振幅和频率呈正相关。Tran[9-11]分别采用重叠网格技术的CFD 方法、BEM 方法以及GDW 方法对带有平台运动的NREL 5MW 风轮进行了非定常气动特性分析,研究表明,三种方法模拟得到的气动功率和推力在小幅度纵摇运动(如1°~2°)情况下显示出良好的一致性,而对于4°振幅的平台纵摇运动下的气动功率和推力,CFD方法与其他两种方法之间存在约15%的差异。Lienard[12]也采用了CFD方法,通过研究NREL 5MW 风电机组在平台纵摇(A=4,8°,T=10s)运动和纵荡(A=8,16m,0.1Hz)运动的研究发现,平均推力在平台纵摇运动下并没有明显变化,而平均功率受平台运动影响较大;纵荡运动与纵摇运动有着相似的变化规律。陈子文、王晓东[13-15]等人采用了带有动态网格和滑动网格耦合技术的非定常计算流体动力学模型,研究了浮动式海上风电机组在不同周期和振幅的平台纵荡、纵摇以及两者耦合运动下的气动特性。其非定常气动分析表明:振幅和频率的增加加剧了风力机整体气动性能的波动。功率输出比陆上风电机组多13.4%。Lin[16]采用CFD 方法,基于NREL 5MW 风电机组,通过纵荡、纵摇以及横荡运动的研究发现,功率和推力的最大值比固定基座的总体性能更高,且耦合运动使得总体性能出现周期性变化,并且波动程度更大,尾迹出现不对称性。Lebel[17]基于CFD 方法研究了DTU 10MW模型在余弦规律纵摇运动下(A=5°,T=8.8s)与动态偏航下(A=3°,T=8.8s)的气动功率和推力变化,研究表明:在11m/s 的风速下,纵摇运动下的平均功率输出增加了32.8%,推力却没有明显的变化,而且会出现涡环状态;相同风速下,动态偏航较固定偏航有着2.5%的平均功率增加。CFD模拟的结果可以给出更丰富的绕流结构信息,但其计算量大,处理多自由度运动网格技术还存在较大困难。
上述研究大多集中在平台的纵荡和纵摇运动,而很少受研究平台横摇运动以及多自由度运动耦合的影响,因此研究漂浮式风电机组多自由度运动下的气动特性具有现实意义。本文采用自由涡尾迹法作为气动计算模型,以OpenFAST 软件为仿真平台,NREL 5MW[18]风电机组模型为研究对象,研究平台单独纵荡、纵摇、横摇运动以及纵荡-横摇、横摇-纵摇、纵荡-纵摇-横摇等耦合运动下对该风电机组气动功率与推力的影响。
1 计算方法与模型
1.1 方法介绍
OpenFAST是NREL实验室开发的可用于求解风力机气-弹-水控制多物理场耦合的开源软件,主要包括气动载荷、结构载荷、控制模块、来流风模块和水动力模块。气动模块中叶片载荷的计算是基于带有叶尖、轮毂损失和尾迹修正以及Beddoes-Leishman 失速模型的动量叶素理论(BEM)、广义动态尾流模型(GDW)以及自由涡尾迹(FVM)方法。自由涡尾迹指尾迹涡元随尾迹流场自由运动,尾迹涡元空间位置作为流场解的一部分。由尾迹形状的生成方法,求解尾迹涡元的空间位置的方法主要分为三种:预定尾迹法、刚性尾迹法和自由涡尾迹法。自由涡尾迹方法允许尾迹涡元自由变形和运动,对于风电机组的复杂流场,自由涡尾迹法有较大优势,因此本文采用自由涡尾迹方法,简称FVM。
自由涡尾迹包含气动和涡尾迹两部分,气动部分本文采用非线性升力线模型,即使用附着涡线模拟叶片的气动效应。如图1 所示,根据升力线原理,叶片由一条变强度附着涡线构成,将其离散为若干等强度涡线。在涡强变化剧烈的叶根和叶尖处需要有更高的单元密度。依据Helmholtz 定律和Kelvin 定律,附着涡环量沿叶片展向变化会产生尾涡(trailing vortex),随时间发生变化会产生脱落涡(shed vortex)。尾涡和脱落涡流向下游形成风轮涡尾迹。

图1 叶片升力线及尾迹涡线示意图[19]Fig.1 Schematic of the lifting line of blade and vortex filament of wake[19]
基于Kutta-Joukowski 升力定理和翼型升力系数建立方程组求解出升力线附着涡环量,解出附着涡环量后即可根据气动力计算方法进行气动力计算。同时采用Du-Selig 失速延迟模型和Beddoes-Leishman 动态失速模型,保证计算准确性。
自由涡尾迹模型是把尾迹涡元的空间位置作为解的一部分,与风附着涡环量的求解过程构成迭代计算,计算起点以叶片启动时刻为准,直到尾迹几何残差和叶片环量值收敛为止。尾迹涡系通过涡环构成,计算过程假设涡环的环量值从产生到结束保持不变。自由涡尾迹控制方程如下:

式中,ψ为风轮旋转相位角;ζ为尾迹网格节点与叶片尾缘夹角;r为尾迹涡系的空间位置矢量;Ω为风轮转速,r/min;采用时间步进计算方法求解自由涡尾迹控制方程,并且使用Lamb-Oseen涡核模型及其涡核增长模型保证计算的准确性[20]。
1.2 计算模型
计算采用的是NREL 5MW 风电机组,NREL 5MW风电机组为上风向3叶片的风电机组数字样机,采用变速变桨的运动控制方式。叶片中内叶展截面采用DU系列翼型,外叶展截面采用NACA64系列翼型。叶片全长61.5m,对应风轮直径126m,轮毂高度约90m。额定风速11.4m/s,额定转速12.1r/min。
以下所有算例均采用稳态风11.4m/s,风电机组转速为12.1r/min。平台运动通过对OpenFAST 代码二次开发实现。平台运动形式(纵摇、纵荡及横摇)为正弦运动,频率选取为0.1Hz,如图2 所示,横坐标表示平台运动方位角,纵坐标表示平台运动的位移(角度)。其中平台纵摇运动中,旋转轴原点位于平台的几何中心,即位于风轮轮毂下方90m 处。浮式平台运动工况见表1。Pitch、Roll 和Surge 分别代表单独的纵摇、横摇和纵荡运动;Pitch-Surge、Pitch-Roll和Surge-Roll表示纵摇、纵荡以及横摇之间的2 自由度耦合运动;Pitch-Roll-Surge 表示三者耦合运动。Ap,As,Ar分别表示平台纵摇、纵荡运动以及横摇的振幅。

表1 平台运动工况Tab.1 Platform motion conditions
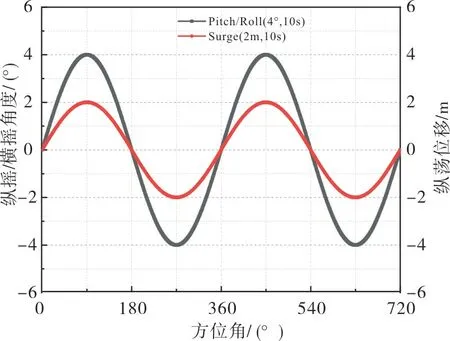
图2 平台运动规律Fig.2 Variation of platform position
2 结果与分析
2.1 模型验证
因NREL 5MW 为数字参考样机,无实验结果。因此使用FVM 方法与文献[18]中的功率和推力曲线进行对比(如图3、图4所示),以验证自由涡尾迹模型的准确性。可以看出FVM 方法计算结果与文献结果基本吻合,表明本文采用的FVM 方法对功率和推力的预测具有较高的可信度。

图3 功率对比Fig.3 Power comparison

图4 推力对比Fig.4 Thrust comparison
2.2 总体性能
2.2.1 平台单自由度运动影响分析
对平台纵荡运动下风电机组的功率和推力进行分析。图5 表示不同振幅的纵荡运动下功率和推力随平台运动方位角的变化。如图所示,功率输出和推力展现出周期性波动,并且周期与平台纵荡运动的周期相同。原因在于纵荡运动所产生的诱导速度,导致功率的波动。功率和推力在180°和540°位置处最大,此时风轮的相对速度最大;而功率和推力在360°和720°位置处最小,风轮相对速度最小。对比图6 的曲线得出,纵荡幅值较大时的功率和推力波动明显大于纵荡幅值较小时的功率和推力波动。原因在于相同的纵荡频率下,纵荡幅值越大,相对速度就越大。图6 表示额定风速时,平台纵摇运动下,采用自由涡尾迹法得到的功率和推力曲线,与纵荡运动相似,在较低纵摇振幅的功率和推力的波动都明显小于较高纵摇振幅的影响,但是功率和推力波动的幅度都明显大于纵荡运动的作用。原因在于平台纵摇产生的相对速度远大于纵荡运动产生的相对速度。
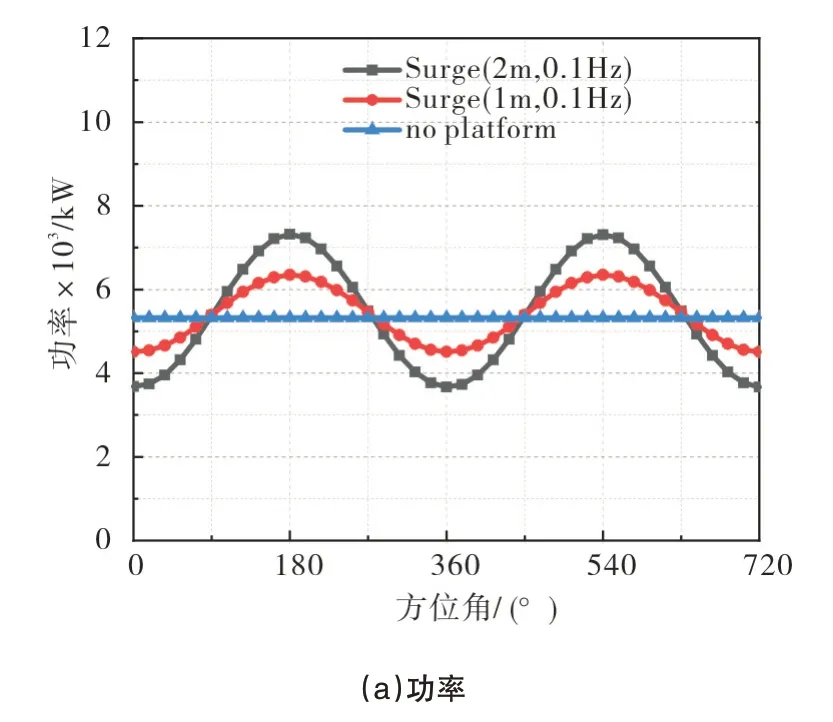

图5 纵荡运动下功率和推力变化Fig.5 Variation of power and thrust under surge motion

图6 纵摇运动下功率和推力变化Fig.6 Variation of power and thrust under pitch motion
表2 给出了一个平台纵荡周期内功率和推力的极值和均值。由图可知,纵荡运动时,平均功率随着平台纵摇运动幅值的增大而增大,且均大于额定功率;而平均推力值虽然都高于额定推力,但相差不大。表明在时均数值层面,推力的大小与振幅无关。当振幅增加时,平均功率输出略有增加,而平均推力基本不变,但推力的剧烈波动会显著增加风电机组叶片的疲劳载荷,严重影响其使用寿命。表3给出了平台纵摇运动周期内功率和推力的最小值、平均值和最大值。由图可知,与纵摇运动相似,平均功率也会随着振幅的增大而增大;而平均推力则不同,平均推力会随着振幅的增大而减小,且4°振幅下小于额定功率。

表2 纵荡运动下功率和推力的极值与均值Tab.2 Extreme and mean values of power and thrust under surge motion

表3 纵摇运动下功率和推力的极值与均值Tab.3 Extreme and mean values of power and thrust under pitch motion
图7给出了风轮在f=0.1Hz平台横摇运动过程中功率和推力的变化规律。结果发现功率的变化规律在两个振幅下呈现正弦的变化特性。与平台纵摇运动相比,功率的推力变化不明显,对于Ar=1°,观察到很小的波动,最大功率与额定功率相差仅为1.6%,推力也是一样。由于风轮的来流速度在旋转平面的投影保持不变,功率波动是由于平台横摇运动在旋转平面的速度分量所致,振幅越大,旋转平面内的弦向诱导速度越大,表现为总体性能波动强度偏大。表4 展示了纵摇运动下功率和推力的极值与均值,可以看出,1°、4°功率的平均值对应波动幅值分别为平均功率的0.9%和0.5%,与额定功率相差很小,表明横摇运动不会影响平均功率的输出;平均值推力对应波动幅值分别为平均功率的0.6%和0.1%。综上所述,与纵摇运动相比,横摇运动对输出功率和推力的影响不明显,可忽略不计。

表4 横摇运动下功率和推力的极值与均值Tab.4 Extreme and mean values of power and thrust under roll motion

图7 横摇运动下功率和推力变化Fig.7 Variation of power and thrust under roll motion
2.2.2 平台耦合运动影响分析
为了进一步研究不同平台运动对海上风电机组输出功率和推力的影响,本节讨论平台耦合运动的影响。首先研究平台纵摇-纵荡耦合运动对功率和推力的影响,图8 为不同振幅下纵摇-纵荡耦合运动下功率和推力随平台运动方位角的变化图,表5显示了二者的极值和均值。可以看出与单独纵摇运动(工况3,工况4)相比,1°振幅的平台纵摇与纵荡运动耦合(工况7,工况8)时,波动的幅值都有了明显的增长,并且提高了平均功率,略微降低了平均推力,4°振幅的平台纵摇与纵荡运动耦合(工况9,工况10)时,平均功率变化不明显,平均推力明显降低。也就是说小幅度纵摇-纵荡耦合运动会提高平均功率输出,对平均推力影响不大;而大幅度平台纵摇-纵荡耦合运动对平均功率输出影响不大,但会减小风电机组的平均受力。

图8 纵荡-纵摇运动下功率和推力变化Fig.8 Variation of power and thrust under combined surge-pitch motion

表5 纵荡-纵摇耦合运动下功率和推力的极值与均值Tab.5 Extreme and mean values of power and thrust under combined surge-pitch motion
图9展示了平台纵摇-横摇耦合运动影响下的功率和推力随平台运动方位角的变化曲线,可以观察到与单独纵摇运动相比,在小幅度耦合运动(工况11~工况13)下,功率和推力变化不明显,平均功率与平均推力略有增加;大幅度耦合运动(工况14)下提高了总体功率与推力的上限,但对下限影响较小,平均功率和推力分别增加了约8.5%和5.2%(见表6)。因此,较小程度的平台纵摇-横摇耦合运动对总体性能影响较小,但其主要以纵摇运动为主;而较大程度的纵摇-横摇耦合运动会增加平均功率与推力输出,横摇运动的影响不容忽视。

图9 纵摇-横摇运动下功率和推力变化Fig.9 Variation of power and thrust under combined pitch-roll motion

表6 纵摇-横摇耦合运动下功率和推力的极值与均值Tab.6 Extreme and mean values of power and thrust under combined pitch-roll motion
图10 为平台纵荡-横摇耦合运动下的功率和推力曲线,可以看出与其他耦合运动相比,纵荡横摇耦合运动对功率和推力的影响不明显。耦合运动与单独纵荡运动相比,平均功率最大相差不到0.5%,平均推力最大相差不到0.16%,见表7。因此,纵荡-横摇运动的耦合以纵荡运动为主,横摇运动的影响可以忽略不计。
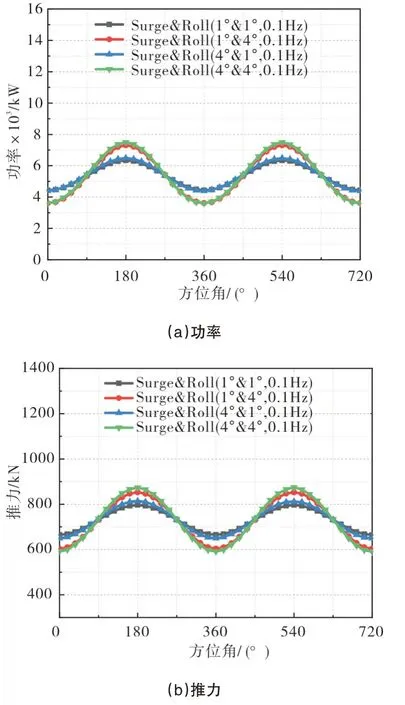
图10 纵荡-横摇运动功率和推力变化Fig.10 Variation of power and thrust under combined surge-roll motion
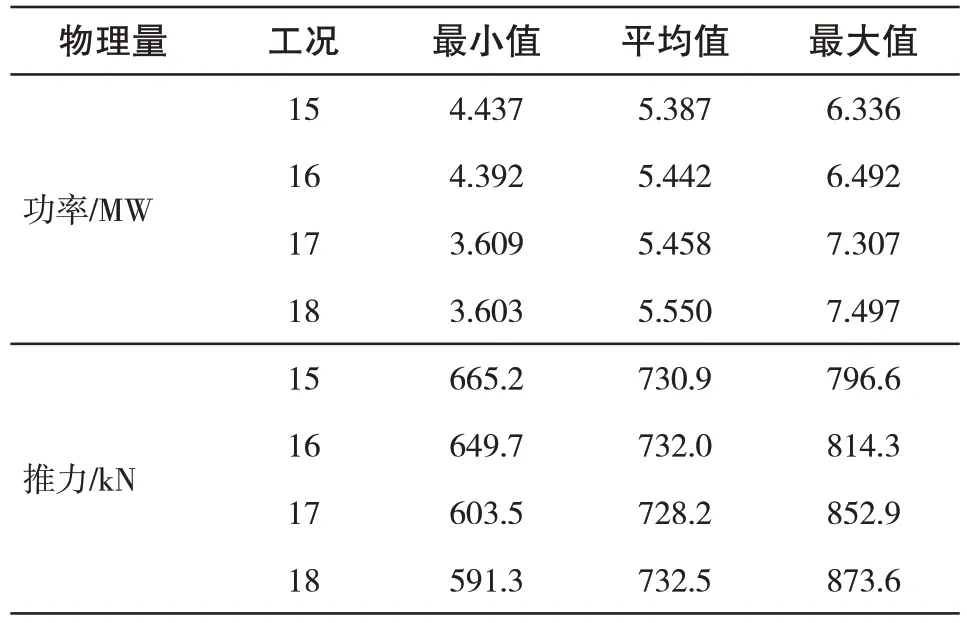
表7 纵荡-横摇耦合运动下功率和推力的极值与均值Tab.7 Extreme and mean values of power and thrust under combined surge-roll motion
前面已经讨论了平台纵荡-横摇、纵荡-纵摇以及横摇-纵荡耦合运动对功率和推力的影响,下面讨论平台纵摇-横摇-纵荡耦合运动下风电机组功率和推力的变化规律。从上文可知,小幅度的平台横摇运动的影响很小,因此,取Ar=4°较大幅度的横摇运动与其他两种平台运动耦合进行计算分析,见工况19~工况22。图11 为这四种工况下的功率和推力变化图。表8 展示了功率和推力的极值与均值。可以看出剧烈的平台三自由度耦合运动(工况22)下的最大功率为12.65MW,达到了额定功率的两倍以上,最小功率仅为526kW,平均功率达到所有工况的最大值。此外,与纵摇-纵荡耦合运动(工况10)相比,耦合运动使得平均功率升高了4.5%。同时对比工况19 和工况20,可以看出平均功率随着纵荡幅值的增大而增大,而平均推力正好相反。对比工况21 与工况22 有着相同的结论。因此,纵摇-横摇-纵荡耦合运动中,纵荡振幅的增大虽可以提高平均功率输出,却会减少风电机组的平均受力。

图11 纵摇-横摇-纵荡耦合运动下功率和推力变化Fig.11 Variation of power and thrust under combined pitch-roll-surge motion
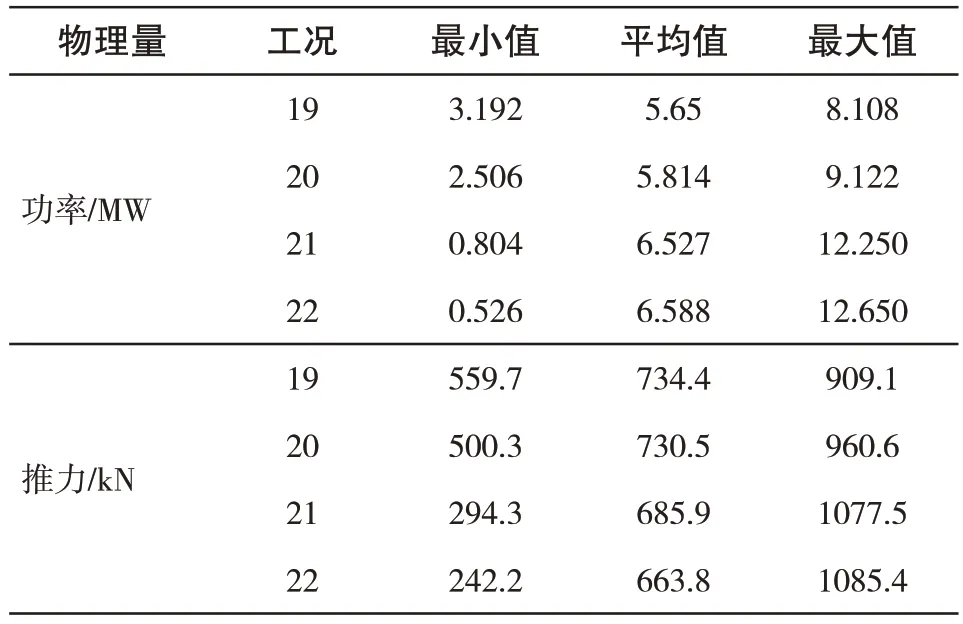
表8 纵摇-横摇-纵荡耦合运动下功率和推力的极值与均值Tab.8 Extreme and mean values of power and thrust under combined surge-roll motion
3 结论
本文基于自由涡尾迹方法建立了漂浮式风电机组气动模型,并且采用建立的气动模型对NREL 5MW风电机组进行了平台纵荡、纵摇、横摇以及耦合运动下的模拟研究,结果表明:
1)浮式平台的运动会导致风电机组功率和推力的波动,在本研究中,纵摇-横摇-纵荡耦合运动对应最大功率波动达到额定功率的两倍以上,最大推力的波动几乎达到额定推力的1.5倍。因此,海上风力发电机组需要采用先进的控制策略来降低电网的不稳定性和疲劳载荷。
2)平台单自由度运动下,平台运动振幅的增大会增加三种平台运动对风电机组功率和推力的影响,并且平台纵摇运动的影响最大,横摇运动的影响最小。
3)对于纵摇-横摇耦合运动,较小程度的耦合运动对功率与推力的影响较小,但其主要以纵摇运动为主;而较大程度的耦合运动会增加平均功率与推力输出,横摇运动的影响不容忽视。而对于纵荡-横摇运动来说,主要以纵荡运动为主,横摇运动可以忽略不计。
4)与平台单自由度运动相比,平台耦合运动会显著增大平均发电量。纵摇-横摇-纵荡耦合运动中,纵荡振幅的增大可以增加平均功率输出,并且减少风电机组的平均受力。
