氢燃料电池空压机叶片扩压器迎角对气动性能影响研究*
2022-05-09李育金熊万里彭思进孙宇杰
李育金 熊万里 彭思进 孙宇杰
(湖南大学机械与运载工程学院)
0 引言
氢燃料电池汽车是以燃料电池为动力源的新能源汽车,具有零排放、低噪声、能量转化效率高等优点,将是未来汽车的发展方向,汽车在匀速、变速和上下坡等不同行驶工况下,需要燃料电池系统输出的功率不同[1-2]。根据相关研究,燃料电池系统的输出功率与氧气进入该系统时的流量和压力有关[3-5]。而车用离心式空压机是燃料电池系统氧气供应侧的核心部件,为系统提供着一定压比和流量的空气,具有体积小、压比高、流量范围宽和效率高等优点,与燃料电池系统有很高的契合度,将会是今后燃料电池车用空压机发展的主流[6-8]。
为了满足燃料电池汽车各个工况的功率需求,要求输入的空气具有更广的流量和压力范围,进而要求离心式空压机具有更宽的工作范围和更高的压比,提高空压机与燃料电池系统的匹配性。叶轮是离心式空压机对气体直接做功的唯一部件,根据欧拉方程[9],理论上叶轮的线速度越高,空压机能达到的压比越大,因此本文对叶轮转速为95000r/min 的离心式空压机进行研究。相关研究表明,叶轮出口处气体动能约占总输入功的30%至40%[10],随后气体进入扩压器将动能转化为燃料电池系统所需要的静压能。所以离心式空压机气动性能主要受离心叶轮和扩压器的影响,通过优化两者的匹配性,可以提高气体动压转化为静压的能力,降低总压损失,获得较高的总压恢复系数,提高离心式空压机的气动性能[11]。
为实现离心叶轮与扩压器的最佳匹配,国内外研究人员对扩压器进行了一系列的研究。班海波等人[12]通过构建叶轮和扩压器的最大流量系数的等式关系,对两者进行匹配,计算出扩压器的最佳喉口面积,使叶轮和扩压器在同一个流量下发生堵塞。S.Lieblein[13]对常规扩压器叶片的低速气动特性进行分析,在低损耗区域内,初步构建了扩压器进口气流冲角与出口气流落后角的经验公式。李庆阔等人[14]对原型为楔形的扩压器进行数值研究,以扩压器子午流道的Vt和Vm作为气动优化的控制参数,提出控制Vt和Vm的分布规律是优化扩压器的关键。S.M.Gunadal[15]对低稠度叶片扩压器中叶片倾斜角对稳定工作范围的影响进行了数值研究,发现叶片尾缘沿叶高的方向倾斜一定的角度时有利于提高空压机的工作范围。刘火星等人[16]在低速叶栅风洞中对NACA65叶型进行气动性能的实验研究,发现叶片前缘为椭圆形的时候比圆形更能有效抑制流体的分离。倪钰鑫等[17]对扩压器进口无叶段的长度进行研究,发现无叶扩压段越长,扩压器性能越低,合适的范围在扩压器子午高度的47%~93%。
在叶轮与扩压器的匹配性设计中,目前已有的研究多针对低中转速下的离心式空压机,对于高转速且用于燃料电池汽车的研究较少。在对带叶片扩压器的高速离心式空压机进行研究时,发现扩压器迎角对空压机的气动性能有着显著影响,本文对某款高速离心式空压机的气动性能进行数值分析,在不改动叶轮的前提下,研究扩压器进口迎角对整体气动性能的影响规律,并优化叶轮与扩压器之间的参数匹配,提出适用于氢燃料电池的高速离心式空压机的迎角范围,为后续的研究和实验提供参考。
1 研究对象
本文的研究对象是某款单级带叶片扩压器的高速离心式空压机,适用于80~100kW 的车载燃料电池系统,为系统输送一定压比和流量的空气。表1给出了该空压机的设计参数,叶轮和扩压器的三维模型及其流道子午面如图1所示。

表1 空压机的设计参数Tab.1 Design parameters of air compressor

图1 叶轮和扩压器的三维模型及其子午流道Fig.1 3D model of impeller and diffuser and its meridional channel
本文研究所用的扩压器叶片为NACA65系列翼型,该系列翼型是由美国国家航空咨询委员会开发的一个翼型族,叶片流动损失小,变工况性能好,广泛应用于高亚音速和超音速的工况,详细的设计参数参考文献[10,18,19],翼型模型如图2 所示。迎角(angle of attack,AoA)为来流速度矢量方向与翼型弦线的夹角,具体关系如式(1)所示,式中翼型安装角γ为弦线与额线方向的夹角[20],进口气流角α为来流速度矢量与圆周方向的夹角。根据数值大小,迎角有正负之分,正迎角表示来流冲向扩压器叶片的工作面(凸面),负迎角表示来流冲向叶片的非工作面(凹面)。

图2 扩压器叶片翼型示意图Fig.2 Schematic diagram of diffuser blade airfoil

根据扩压器的进口气流角和式(1)调整翼型安装角以获得不同迎角的叶片扩压器,取迎角的间隔为1°,计算完成了叶片扩压器迎角范围在-4°~4°之间的9组仿真。
对于在同一转速下的叶轮和叶片扩压器,不同流量时的迎角大小是不一致的,为避免不必要的麻烦以及方便行文,本文所说的迎角值均是指设计工况(即转速95000r/min、流量140g/s)下扩压器来流速度矢量与翼型弦线的夹角,即式(1)中的α为定值,具体数值可根据单叶轮的仿真结果得出。
2 网格划分及计算设置
2.1 网格划分
利用NUMECA软件对叶轮和扩压器进行网格划分并计算求解。为了更好的模拟湍流流动,对于增强型壁面的湍流附面层的粘性底层,要求壁面无量纲网格尺度y+<15,然后通过计算第一层网格厚度y1来获得合理的网格[21-22]。叶轮与扩压器的展向网格层数均设为57 层,将叶轮出口的相关参数代入式(2)中,可以计算得扩压器壁面的y1<3.8e-6m,取y1=3e-6m。

式中,Rex为雷诺数;ρ为流体密度;U为流体的时均速度;L为边界层参考尺寸;μ为流体的动力粘度;Cf为壁面摩擦系数;τw为壁面剪切应力;uτ为壁面摩擦速度。
图3 是叶轮和扩压器叶片的y+云图,由于叶轮出口流速较高,因此叶轮叶片尾缘处y+值较大,但y+值均小于15,近壁面网格尺度满足要求。

图3 叶轮和扩压器叶片的y+云图Fig.3 y+cloud diagram of impeller and diffuser blades
B2B网格划分采用默认的O4H拓扑结构,经网格无关性验证之后,整个计算域网格数目将近171 万,其中叶轮通道网格110万,扩压器通道网格61万,计算域网格如图4所示。为了获得高质量网格,提高求解器的计算精度和运算速度,则需要保证:1)最小网格正交性>20°;2)最大网格长宽比<1000;3)最大网格延展比<5;4)最大网格偏转角<40°。最终网格质量如表2所示。

表2 计算域网格质量Tab.2 Grid quality of computing domain

图4 计算域网格划分Fig.4 Grid division of computing domain
2.2 计算设置
湍流的控制方程选用三维雷诺平均Navier-Stokes方程,同时采用鲁棒性较强、求解速度快的Spalart-Allmaras湍流模型作为补充,使用中心差分格式将计算区域离散化;将叶轮设置为转动件,转速为95000r/min,叶轮进口导流管和扩压器设置为固定件,转速为0;边界条件给定进口总温298K、总压101.3kPa,轴向进气,出口给定质量流量和计算的初始静压;根据实际情况设置初场,本文中进口截面估计静压为95kPa,转静子面的估计静压为110kPa,迭代步数为800 步,收敛残差初始值为1e-6。
从以下三个方面判断计算结果是否收敛:1)模型的全局残差达到标准,一般残差值低于1e-4 也可以认为全局残差已经收敛;2)各个物理变量的计算结果趋于稳定;3)进出口质量流量的差值小于0.5%。若同时满足这三个要求,则可以判定模型的计算结果已经收敛。
3 计算结果及分析
由式(1)可知,要确定叶片扩压器的迎角大小,需要先获得扩压器进口处来流的气流角。忽略离心叶轮出口与扩压器叶片进口之间的无叶扩压段以及扩压器叶片前缘对气流角的影响,则气流的运动轨迹呈“对数螺旋线”型,叶轮出口气流角等于扩压器来流气流角。表3是单叶轮在设计转速95000r/min下的仿真结果,喘振流量88g/s为压比下降临界点[23],此时压比最高为4.2,从表中可知单叶轮仿真时的稳定工况区在88~181g/s之间,设计点140g/s处的出口气流角为α=16.5°。

表3 单叶轮在设计转速下的仿真结果Tab.3 Simulation results of single impeller at design speed
3.1 不同迎角对空压机工作范围的影响
图5 给出了离心叶轮在设计工况下不同迎角的流量-压比特性曲线,取压比最高点作为喘振点,保证空压机具有安全的失速裕度[23]。从图5 可以发现随着迎角的增加,空压机的喘振流量和堵塞流量逐渐增大,其稳定工况区往大流量方向移动,且工作范围呈扩大的趋势,说明空压机的通流能力在增强。除迎角-4°和-3°外,其余各迎角的设计点压比均满足设计要求。当迎角在-4°~1°之间增加时,堵塞流量逐渐增大,由于叶轮结构不变,预测是扩压器在限制空压机的最大通流量;当迎角在2°~4°之间增加时,喘振流量继续往大流量方向移动,但堵塞流量却不再变化,限制在181g/s左右,与表3中单叶轮仿真时的堵塞流量数值一致,所以预测此时堵塞点出现在叶轮内部,是叶轮限制了堵塞流量的增大。
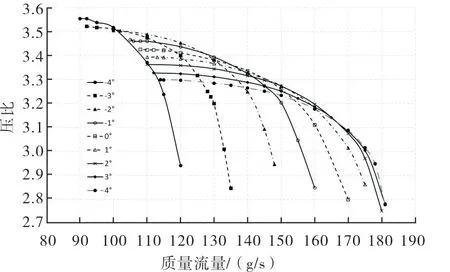
图5 不同迎角的压比曲线对比Fig.5 Comparison of pressure ratio curves at different angles of attack
为了验证上述预测是否正确,同时研究扩压器迎角对空压机工作范围影响,对不同迎角在堵塞工况时流道内的马赫数进行分析,得到了流道子午面91%叶高处的相对马赫数曲线,该叶高处的气流沿流线经过子午面的高马赫数区,便于分析流体的临界状态,仿真结果如图6所示。从图中可以看出迎角在-4°~0°增加时,扩压器流道内的相对马赫数先增大后减小,波峰出现在扩压器归一化长度的40%~50%处,峰值逐渐减小且均大于1,说明在扩压器通道截面的平均流速达到音速,出现堵塞现象。选取其中迎角-4°时扩压器通道的流场进行分析,图7 给出了其堵塞工况下10%、50%和90%叶高处的相对马赫数云图,发现马赫数大于1首先出现在扩压器喉部区域,验证了前文的预测。



图6 不同迎角在堵塞工况时子午面相对马赫数曲线图Fig.6 Relative Mach number curve of meridional plane under choking at different AoA

图7 迎角-4°在堵塞工况时不同叶高处相对马赫数Fig.7 Relative Mach number at different blade heights at AoA=-4°under choking

图8 叶片扩压器进口气流示意图Fig.8 Diagram of inlet air flow of vane diffuser
图9 给出了迎角1°在堵塞工况下不同平面的相对马赫数云图,结合子午面和B2B面进行分析,发现此时高马赫数区同时在叶轮和扩压器的喉部出现,随着正迎角的增加叶轮喉部的马赫数增大而扩压器的减小。堵塞工况下气流从叶轮进口到喉部时,因通流面积的减小,使流速达到当地声速,又因轮盖侧转弯处的气流收敛加剧,且叶顶与轮盖之间存在间隙流,所以气流更容易在叶顶发生分离,恶化流动状态,使流量不能再继续增加。由于没有改变叶轮的结构,其喉部面积不变,所以堵塞流量并不会随着迎角的增加而继续增大,证明了上述分析结果的正确性。

图9 迎角1°在堵塞工况下的相对马赫数云图Fig.9 Relative Mach number at AoA=1°under choking
综合上述的分析可知,高速离心式空压机的堵塞流量由叶轮和扩压器共同决定,更确切地说是由两者的喉部面积决定,因为当流量不断增大时,流道喉部由于截面积最小而使得气流首先在该处达到音速,马赫数达到临界状态,流量不再增加而发生堵塞。扩压器迎角与其喉部面积近似为正比例关系,如图10所示,所以当迎角过小时,扩压器因喉部面积较小而先于叶轮发生堵塞,甚至是未达到设计工况点就提前堵塞或接近堵塞,如迎角-4°~-2°。当迎角增加时,扩压器喉部面积随之增大,堵塞流量也在增大,达到一定数值后叶轮流道先出现堵塞,马赫数达到临界值,此时堵塞点转移到叶轮喉部。为了实现扩压器与叶轮的良好匹配,要求扩压器尽可能地不缩小叶轮的工作范围,通过改变扩压器迎角的大小,使流道的堵塞点位置刚好从扩压器喉部转移到叶轮喉部,此时空压机的工作范围最广,因此可以确定出迎角的最优值在0°~2°之间。

图10 扩压器迎角与其喉部面积的关系曲线Fig.10 Relation curve between AoA of diffuser and throat area
3.2 不同迎角对空压机气动效率的影响
离心式空压机在设计转速下不同迎角的流量-效率特性曲线如图11所示。从整体可以看到随着迎角的增大,效率曲线往大流量、高效率方向移动,稳定工作区范围逐渐扩大。各效率曲线的差异主要是由于扩压器结构的变化而引起的,扩压器的气动效率主要与摩擦损失、冲击损失和分离损失等流动损失有关,所以在综合流动损失最小时会具有最高的效率。排除掉提前堵塞的迎角-4°、-3°和-2°三个方案,对迎角-1°~4°时设计工况的效率进行分析:当迎角增大时,扩压器叶片的安装角随之减小,从几何结构上来看扩压器叶片的通流路径在变短,所造成的摩擦损失减少;但迎角增大至正迎角时,气流会在扩压器叶片的非工作面出现分离现象,增加了分离损失,同时迎角增大还会增加气流与叶片之间的冲击损失。综合来看,迎角增大时所减少的摩擦损失不足以弥补随之增加的分离损失和冲击损失,使得总的流动损失增加,所以设计工况的效率随着迎角的增大而降低,在迎角-1°~0°之间的流动损失最小,故而效率曲线的峰值在设计工况附近。
从图11 中可以看到随着迎角的增大,各效率曲线峰值所对应的质量流量也在不断增大。迎角的增大是通过减小扩压器的翼型安装角来实现的,原流量下的气流速度矢量与翼型弦线之间的夹角变大,增大了流动损失,为了使流动损失重新达到最小,则需要相应地减小扩压器来流的气流角,使其与弦线的夹角变小。由叶轮的出口速度三角形可知,当流量增加时,气流绝对速度的周向分量减小而径向分量增加,出口气流角随之减小,所以当迎角增大时,峰值效率所对应的流量也在增加。

图11 不同迎角的效率曲线对比Fig.11 Comparison of efficiency curves at different AoA
为了更好的评价空压机的性能,定义效率大于70%属于高效率,高效率区范围与100g/s的比值为相对高效区,则不同迎角时空压机气动系统的效率如表4所示。

表4 不同迎角的气动效率Tab.4 Aerodynamic efficiency at different angles of attack
从表中可知,随着迎角的增加,相对高效区、峰值效率和设计点效率均先增大后减小,在迎角1°和2°时的相对高效区比例最大,达57%;迎角2°时具有最大的峰值效率74.3%;迎角-1°的设计点效率最高。对于具有多个使用工况的空压机而言,在提高设计工况效率的同时,还需要扩大高效率区的范围,为了获得高性能的空压机,需要兼顾设计点效率和高效区范围。因此,虽然迎角-1°的设计点效率最高,但是其相对高效区范围比迎角1°小8%,峰值效率小0.3%,而迎角1°与-1°的设计点效率相差不大。综合分析可知,在扩压器迎角0°~2°之间存在某个值,使得扩压器与叶轮的效率匹配性最优,既保证了设计点落在高效率区范围之内,也使得高效率区的范围达到最大,此时空压机的综合效率最高。
4 结论
本文对适用于80~100kW 氢燃料电池的车用离心式空压机进行数值模拟,叶轮设计转速为95000r/min,研究了叶片扩压器迎角大小对空压机气动性能的影响,通过分析不同迎角时空压机的性能曲线和流场云图,得到以下结论:
1)叶片扩压器迎角大小对高速离心式空压机的工作范围具有显著的影响。在设计转速下,正迎角的稳定工作范围比负迎角的大,在较小的正迎角范围内存在最优值,使得空压机的工作范围最宽,流量-压比特性曲线平缓且满足设计要求;
2)随着迎角在-4°~4°之间增加,高效区范围和峰值效率先提高后降低,离心式空压机在迎角0°~2°范围内有最优的综合效率,设计点效率可达73.6%;
3)通过调整迎角大小,可以在不改变叶轮结构的前提下,优化扩压器与叶轮的匹配性能,提高离心式空压机的气动性能和优化设计流程;对于高转速的离心式空压机,叶片扩压器迎角在0°~2°之间具有良好的气动性能。
4)对于不同型号的叶片扩压器,其迎角的最优范围还需要进一步研究,本文结论以及研究思路可为类似的带叶片扩压器的高速离心式空压机的设计提供参考。
