基于时空特征的公交站点短时客流量预测

姚思佳，桂智明，郭黎敏

(北京工业大学 信息学部，北京 100124)

0 引 言

随着城市化进程的脚步不断加快，机动车保有量快速增加，随之而来的尾气污染及交通事故等问题频发[1]。大力提倡乘坐公共交通成为缓解上述问题的重要举措。公交车作为地面公共交通工具，是公共交通中的一个重要组成部分。吸引更多的人乘坐公交出行，是实现城市可持续发展的一条必由之路。近年来，不断增加的公交数据为公交客流的分析和预测带来了技术支持。许多客流预测的方法也从传统的数据浅层预测[2]方法转变为基于数据的深层次挖掘的深度学习方法[3-4]。但是大多数的客流预测方法只考虑了时间维度的特征，未考虑空间维度的相关特征。

目前，时间序列预测最常用的模型是循环神经网络(recurrent neural network，RNN)以及其变体，即长短期记忆网络(long short-term memory，LSTM)[5]和门控循环单元网络(gated recurrent unit，GRU)。杨文淇[6]提出利用LSTM模型对最新建设的城市轨道线路周边的公交客流进行预测，并改进激活函数来提高预测精度。李梅等人[7]利用多种类型数据进行数据特征构造，并用深度长短期记忆网络方法预测地铁进站客流量。

由于LSTM模型更关注的是时间序列，所以此模型在预测客流量时忽略了道路的拓扑结构带来的空间信息。因此对时空特征进行挖掘的模型相继被提出。冯碧玉[8]结合卷积操作和循环操作提取轨道交通客流量的时空特征，并提出了CNN-LSTM组合预测模型，该模型提高了轨道交通进站客流的预测精度。

近年来，图卷积神经网络(graph convolutional network，GCN)被广泛应用于社交网络[9]、计算机视觉[10]、推荐系统[11]以及自然语言处理[12]等领域。图卷积神经网络与传统的卷积神经网络相比，其对于不规则的图结构有着出色的挖掘能力[13]。由于交通路网的复杂性，有时不能将其表示为一个规则的二维结构。此时，图卷积神经网络发挥出其优势，可以挖掘复杂交通路网的空间信息。Liu等人[14]用多种不同的拓扑结构图为轨道交通系统建模，提出一个统一的物理-虚拟协作图网络(PVCGN)，其结合GCN和GRU等网络进行时空特征的学习，实验表明在上海和杭州两地的轨道交通客流预测中，该方法均能展现其优越性。

随着深度学习技术的发展，注意力机制成为学者们关注的热点。注意力机制能够关注更重要的特征。Guo等人[15]提出将注意力机制引入时间和空间特征的提取模块中，并结合图卷积和一维时间卷积来捕捉动态空间和时间的相关性，从而提高交通流量的预测精度。

基于上述分析，可以看出交通领域预测方法正在逐步发展，但是同样也存在不足之处。针对公交客流预测方法缺少对空间特征的运用，该文运用GCN、LSTM以及注意力机制技术，提出了基于注意力机制的图卷积长短期记忆网络预测模型(AGLSTM)。主要贡献如下：

(1)提出AGLSTM模型，该模型利用GCN对复杂公交线网的空间特征进行提取，用LSTM提取时间特征，并利用注意力机制来区分不同时刻特征的重要性。

(2)在北京公交数据集上进行实验验证，并对比了其他传统模型，实验表明提出的模型能够提高公交客流量的预测精度，为公交客流预测提供一定的借鉴意义。

1 基于注意力机制的图卷积长短期记忆网络

AGLSTM组合模型的整体结构如图1所示，该模型主要分为五个部分。第一部分为图的邻接矩阵以及节点的特征矩阵组成的输入部分。第二部分是由图卷积对输入的邻接矩阵以及特征矩阵进行客流量空间特征提取的部分。第三部分将第二部分每个时刻的输出作为输入，通过长短期记忆循环神经网络进行客流量的时间特征提取。第四部分为对LSTM网络各个隐藏状态进行注意力机制变换，充分考虑每个隐藏状态对输出状态的影响。第五部分是全连接层，通过全连接层对提取的数据进行变换，得到最终预测值。

图1 AGLSTM组合模型结构

1.1 输入层构造

根据图卷积神经网络的特点，本模型的输入需要构造公交线网的邻接矩阵以及各节点的特征矩阵。以下分别为两个矩阵的构造过程。

(1)邻接矩阵的构造。

根据公交路线信息和站点信息对公交站点构造道路拓扑结构图，其中图表示为G，V表示所有站点的集合，E表示站点相邻关系的集合。以邻接矩阵的形式存储，邻接矩阵是一个s*s的二维矩阵，邻接矩阵的值为0或1。其中s代表公交站点的数量，行和列分别代表按照公交站点编号顺序排列的站点，邻接矩阵的值中，0代表两个站点不相邻，1代表两个站点相邻，并且邻接矩阵为对称矩阵，这里邻接矩阵记为A。邻接矩阵如公式(1)所示：

(1)

其中，eij取值为1时，表示站点vi与站点vj在某条线路上相邻，eij取值为0时，表示站点vi与站点vj在某条线路上不相邻。

(2)特征矩阵的构造。

针对原始数据进行特征提取，统计得到每个公交站点在每个时段的客流量。为了加快模型训练速度，对公交客流量数据进行最大最小归一化，归一化计算如公式(2)所示：

(2)

其中，x表示归一化后的客流量数据，f表示原始客流量数据，fmax表示原始客流量中最大值，fmin表示原始客流量中最小值。f被归一化到0到1的闭区间。

构建交通数据的特征矩阵X，将归一化后的数据表示成特征矩阵的形式，它描述了每个公交站点的客流量随时间的变化，每行代表一个站点所有时刻的客流量，每列代表同一时段不同站点的客流量。特征矩阵中站点的排列顺序与邻接矩阵中站点特征矩阵的排列顺序相同。

X构建如公式(3)所示：

(3)

其中，横向表示一个公交站点的客流量随时间的变化，t表示时刻的个数，纵向表示所有公交站点在一个时刻的客流量数据，s表示公交站点的个数，矩阵中的元素xst表示第s个公交站点在第t个时刻的客流量。预测模型需要输入邻接矩阵A和特征矩阵X的输入矩阵进行模型训练来输出公交站点在t+1时刻的客流量。

1.2 空间特征提取单元

某个公交站点的客流量不仅仅与其自身的历史客流量有关，还可能与其他站点的客流量有关。公交线网是一个不规则的拓扑图结构，因此选用能提取不规则图结构特征的图卷积神经网络来挖掘交通数据的空间特征。为了加强网络学习时的数值稳定性，引入拉普拉斯矩阵，可以有效防止多层网络优化时出现的梯度消失或爆炸的现象[16]。使用公式(4)表示图卷积操作：

(4)

文中模型采用两层GCN结构，如公式(5)所示：

(5)

1.3 时间特征提取单元

虽然循环神经网络能够建立长时间间隔状态之间的依赖关系，但是由于梯度弥散或梯度爆炸问题，在实际应用中，只能学习到短周期的依赖关系，这就产生了所谓的长期依赖问题。长短期记忆循环单元引入门限机制来控制信息的积累速度，并可以选择遗忘之前部分累积的信息，实现了信息的长时间传递，使之前时刻的信息可以一直参与训练。公式(6)～公式(11)为长短期记忆循环单元的计算过程：

ft=σ(Wfxt+Ufht-1+bf)

(6)

it=σ(Wixt+Uiht-1+bi)

(7)

(8)

(9)

ot=σ(Woxt+Uoht-1+bo)

(10)

ht=ot⊙tanh(Ct)

(11)

1.4 注意力机制单元

长短期记忆循环神经网络每个记忆单元都只与前一时刻隐藏状态有关，在时间序列预测中，距离当前预测时间远的时间点也很有可能对当前预测节点有影响，所以引入注意力机制来对前面各时刻的信息进行权重划分，选择出对当前影响重大的时刻。此时，最后一个时刻的输出状态就取决于前面所有隐藏状态的加权组合，而不仅仅是最后一个隐藏状态。对于长短期记忆循环单元输出的t时刻的隐藏状态ht，采用以下注意力机制的运算逻辑进行计算，注意力机制运算过程如公式(12)～公式(14)所示：

et=Vetanh(Weht+be)

(12)

(13)

(14)

其中，Ve，We为需要学习的参数，be为需要学习的偏置，et表示第t个时刻隐藏状态ht对应的注意力评分值，tanh为激活函数，T表示时刻总个数，αt为通过Softmax函数对所有的et归一化后得到的权重系数，c为对长短期记忆循环单元各个时刻输出的隐藏状态进行了加权，作为最终隐藏状态的输出。

1.5 AGLSTM组合模型构造

根据上述几个小节对各模型单元的介绍，结合AGLSTM组合模型的设计结构，可以得到GLSTM组合模型的运算逻辑，如公式(15)～公式(20)所示：

ft=σ(Wfgc(Xt,A)+Ufht-1+bf)

(15)

it=σ(Wigc(Xt,A)+Uiht-1+bi)

(16)

(17)

ot=σ(Wogc(Xt,A)+Uoht-1+bo)

(18)

(19)

ht=ot⊙tanh(Ct)

(20)

其中，gc(·)表示图卷积操作，其余参数的含义与长短期记忆循环神经网络单元相同，此处不再赘述。Xt表示在t时刻输入的特征矩阵，A表示邻接矩阵。

根据GLSTM组合模型的运算逻辑可以得出GLSTM组合模型单元的内部结构，如图2所示。

图2 GLSTM组合模型单元内部结构

对于每个GLSTM组合模型单元输出的隐藏状态，注意力机制单元会根据其运算逻辑对每个隐藏状态进行评分，得出每个隐藏状态重要性的比例，进而得到用Softmax函数归一化后的权重系数{αt-n,αt-n+1,…,αt}，此权重系数对应于每个隐藏状态。最后将各隐藏状态的权重系数进行相乘相加操作，则得到状态的最终输出。图3为AGLSTM组合模型的内部结构示意图。

该文使用的损失函数如公式(21)所示：

(21)

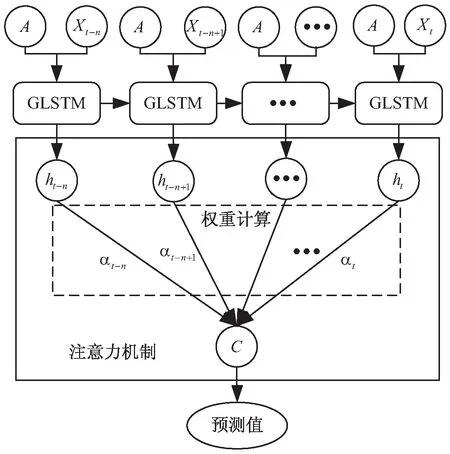
图3 AGLSTM组合模型内部结构

2 模型验证与分析

2.1 实验数据集

为了验证所提出的AGLSTM组合模型的效果，实验选取北京公交4条线路的站点作为研究对象。该数据集包含了北京公交973路、985路、605路、535路 4条存在相同站点的线路数据，其中包含上车刷卡数据、公交线路数据以及公交站位数据。4条线路区分上下行，共8条行驶路线，237个公交站点。图4为4条公交线路的线路图。

图4 4条公交线路

实验数据集为2017年11月的北京公交刷卡数据，选取2017年11月中前20个工作日进行实验，并将前16天工作日的刷卡数据作为训练集，后4天的刷卡数据作为测试集。该实验中选取每天5：00至22：30时间段内刷卡数据，并以15分钟为时间间隔统计刷卡数据，划分后每天得到70个时间段。

2.2 模型相关参数设置

本实验用前7个时间单位的公交客流量对下一个时间单位的客流量进行预测。根据1.1节中对输入矩阵的描述，需要对公交站点按照其相邻情况构造邻接矩阵，以及构造每个站点的由历史时间客流量组成的特征矩阵。

为了更客观地对模型预测结果进行比较，实验采用了两种回归评价指标来评估预测模型的性能，分别为平均绝对误差(mean absolute error，MAE)以及均方误差(root mean square error，RMSE)，计算公式可以表示为公式(22)及公式(23)：

(22)

(23)

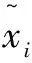
神经网络的训练效果与神经网络的隐藏层的层数以及隐藏层节点数有很大关系。隐藏层节点数是导致过拟合的直接原因，隐藏层节点数与输入输出维度相关，并且每个模型都是不一样的。本实验设置图卷积层与LSTM层的隐藏层节点数相同。首先控制网络中其他超参数不变，改变LSTM隐藏层节点个数，寻找最优节点数。图5展示了LSTM隐藏层个数变化对预测效果的影响。

图5 不同LSTM隐藏层节点个数对模型的影响

其次，批尺寸会直接影响到模型的优化程度和速度，也影响GPU的显存利用率，对于模型预测准确率有明显影响。因此，控制其他超参数不变，LSTM隐藏层个数为48，调整批尺寸大小，以达到模型最优。图6展示了不同批尺寸对模型预测结果的影响。

图6 不同批尺寸大小对模型的影响

通过观察图5以及图6可以发现，LSTM隐藏层节点个数为48，批尺寸为48时，模型的误差最小，因此，最后将AGLSTM模型的实验参数设置为LSTM隐藏层节点个数为48，批尺寸为48，初始学习率为0.001，学习衰减率为0.9，迭代次数为2 000，并采用Adam优化器[17]。

2.3 模型预测结果对比

将提出的AGLSTM模型与HA模型、SVR模型、CNN模型[18]、LSTM模型以及GLSTM模型进行预测效率对比。HA(history average)模型是历史平均模型，其将前几个时间序列取平均作为下一个时间序列的预测值。SVR(support vector regression)模型是支持向量机回归模型，其利用核函数来实现回归预测。CNN(convolutional neural networks)模型是卷积神经网络模型，其利用卷积操作和池化操作进行特征的提取。LSTM模型是长短期记忆网络，是一种常用的时序预测模型，其对前面时刻的信息进行保留或遗忘，以克服长期依赖问题。GLSTM模型是AGLSTM去掉注意力机制的模型。表1为各模型的预测结果误差。

表1 模型预测性能对比

通过分析表1可知，AGLSTM模型的RMSE和MAE相对于其他对比模型都要小，对比效果较好的LSTM模型，AGLSTM模型的RMSE和MAE分别降低了2.99%和1.60%。相较于其他对比模型，AGLSTM模型预测效果更好。LSTM预测模型对时间序列的预测效果表现较好，但是其忽略了空间上的一些特征，所以预测效果不如AGLSTM模型。CNN模型更善于挖掘空间上的特征，但是公交客流更多的是在时间上有一定规律，所以预测效果不如LSTM模型。对比基于统计学理论的HA模型及机器学习方法SVR来说，深度学习的方法能够挖掘深层次的特征，所以其预测效果更好一些。提出的GLSTM模型和AGLSTM模型对比其他模型都有较好的效果，这两个模型对比，可以说明引入注意力机制能够提高模型的预测精度。

3 结束语

针对以往公交客流量预测中不能充分利用时空特征的问题，提出了一种能够同时考虑时间和空间两个维度特征的AGLSTM模型，来预测公交站点短时客流量。该模型首先利用图卷积神经网络能够提取不规则图结构特征的特点，来捕获复杂的公交线网中各站点的空间联系。其次，将图卷积神经网络提取出的空间特征输入LSTM中，进一步进行时间维度特征的提取。由于循环神经网络单元只输出最后一个时刻的隐藏状态，所以引入注意力机制来计算不同时刻特征对输出时刻特征影响的重要性。经过分析该模型与其他对比模型的预测结果，证明该模型能够提高预测精度。