一种基于有偏估计的飞机备件需求预测模型

刘登一,侯胜利

(1.空军勤务学院 研究生大队，江苏 徐州 221000； 2.空军勤务学院 航材四站系，江苏 徐州 221000)

1 引言

备件是影响维修保障能力的关键因素，其筹、储、供、管等方面决策的科学性与合理性，对于确保装备正常运转具有重要的作用[1]。现代化高科技的局部战争对飞机备件保障提出了更高的要求，如何在资源经费有限条件下提高飞机备件保障能力，成为了近些年来战斗机保障的突出问题。

为了实现对飞机备件快速准确的预测，需要运用降维思想对大量的备件消耗数据进行分析转换，在所有特征变量中提取最能反映需求的主要成分，实现对特征空间的压缩，提高数据的运算速度。关于飞机备件的预测问题，国内外的诸多研究者进行了深入的分析。常见预测模型有支持向量机模型、人工神经网络模型、灰色模型、时间序列预测模型等。例如，文献[2]利用非参数回归进行航材消耗的预测，对新机航材消备件消耗预测性较好，但由于数据较少、没有综合考虑多方因素，无法准确把握飞机备件消耗的影响因素；文献[3]利用GM(1,1)对新机备件进行需求预测，对于不确定性的新机备件消耗预测效果较好，但灰色模型没有考虑消耗的随机性问题，对中长期的预测精度较差；文献[4]利用人工神经网络对民航航材备件需求数据进行预测，模型预测结果误差小、精度高，对非线性特点的航材需求具有较好的适应性，但神经网络算法种类较多，且运行速度随着模型复杂度和数据量的增加而极具变慢，不易作为计算机算法在航材业务系统中嵌入应用[5]，且神经网络容易陷入局部最小值，从而使得训练没完成就已经结束[6]。与国内备件预测方法不同，美军利用美空军提出的METRIC及其扩展模型，对初始备件进行预测，并以需求数据库为基础，利用加权滑动平均法对正常供应阶段的备件需求进行预测。尽管对GM(1,1)和神经网络等预测模型有了相当的研究，但在飞机备件预测中也没有推广应用，究其原因，这类模型计算体系复杂，只有对不同种类、不同寿命阶段以及不同影响因素下的备件运用恰当的优化算法对参数进行优化，才能取得较好的预测效果，而对于数量占比巨大且符合多重共线性需求规律的消耗品和部分价值较高且易磨损的可修复备件来说，这类模型的计算速度慢，因此在实际应用中效果并不理想。

针对飞机备件需求影响因素较多、指标体系复杂等特点，本文提出了一种基于有偏估计的航材需求预测模型，综合考虑了影响备件需求不同影响因素之间的关联性，通过主成分分析(principal components analysis,PCA)对数据降维，利用岭回归[7]方法进行预测，有效提升了运算速度，预测精度与其他模型相差很小，且模型简单且易于运行，既符合飞机备件需求预测的精度要求，又提高了计算速度，为大数据下飞机备件需求的预测提供了一种简单可行的模型。

2 基于有偏估计的预测模型

主成分分析(PCA)是一种非监督学习的降维技巧，它能将大量的相关变量转化成一组很少的不相关变量，这些无关变量称为主成分[8]，并利用投影矩阵将高维信息数据映射到低维空间，并期望在所投影维度上数据的方差最大，在信息量不丢失的前提下，对原始数据进行降维，旨在使用较少的数据来反映原始数据的特性[9]。累计方差解释比率反映了前k个主成分所代表的原始指标信息的百分比，一般要求累计方差解释比率不少于85%。在实际问题中，主成分的选取，需要综合计算速度和预测准确性来决定。

A.E.Hoerl在1962年首次提出岭回归方法，用以控制与最小二乘估计相关的方差膨胀性和产生的不稳定性。A.E.Hoerl和R.W.Kennard[10]对岭回归给出了具体的分析与证明。岭回归与最小二乘法十分相似，但与最小二乘法相比，岭回归采用有偏估计进行参数估计，最大优势就在于它综合权衡了误差与方差[11]，它放弃了最小二乘法的无偏性，以损失部分信息降低精度为代价获得回归系数，因此，它是更符合实际、更可靠的回归方法。

本文将用主成分分析法(PCA)来实现数据的降维，这里直接调用R语言中的prcomp()命令进行主成分分析，主成分分析的算法以及具体实现见文献[11]。有偏估计模型的实现主要分为两步：一是通过PCA对变量进行降维；二是利用岭回归方法对测试集数据进行预测。

2.1 主成分分析降维

设有n个预测变量，x1，x2，x3，…,xn分别代表每个预测变量的n种特性，对有N个训练样本的训练集来说，则可用N×n矩阵表示。由于预测变量之间的指标体系和单位数量级不同，因此需对数据按式(1)进行标准化处理，生成标准化矩阵Y，即：

(1)

(2)

式(2)中，rij为标准化矩阵Y中的yi和yj的相关系数，且rij=rji。利用得到的rij生成相关系数矩阵RN×n，之后对特征方程|λI-R|=0求解，求出特征值λn，然后按大小顺序进行排序，即：

λ1≥λ2≥λ3…≥λn≥0

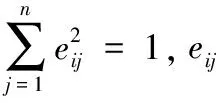
(3)

在主成分选取时，应首先考虑方差的解释比率(PVE)，一般情况下，取累计PVE达到85%～95%的主成分，其次应综合衡量计算速度和准确性，选取主成分尽可能少，累计PVE多且精度相对高的主成分，主成分数量的选取可参考本文最后的算例。

2.2 岭回归方法预测

设x1，x2，x3，…,xn是标准化变量，标准化过程按式(4)处理。

(4)

与最小二乘法不同，岭回归估计为：

β(k)=(XTX+λI)-1XTY

(5)

式(5)中：XTX为x1，x2，x3，…,xn的相关系数矩阵；β为岭回归估计；I为单位矩阵；λ(λ≥0)为岭回归参数。当自变量之间存在复共线关系时，|XTX|≈0，最小二乘估计求得的回归系数会出现与实际情况很不符合的异常现象，而XTX+λI接近异常的程度会比XTX接近异常的程度小得多，即最小二乘在复共线状态下的偏差部分虽然为零，但它的方差部分却很大，最终致使它的均方误差很大，而岭回归是牺牲无偏性，换取方差部分的大幅度减少，最终降低其均方误差。

本文利用十折交叉检验的方法对进行筛选，最终得到使交叉检验误差最小的值。

3 基于有偏估计的预测模型用于飞机备件需求预测

首先对数据进行适用性判别，并利用主成分分析法对含有多个影响备件需求的变量进行筛选，得到对飞机备件需求量影响较大的几个主成分，将计算后的因子作为岭回归模型的输入变量，最终得到主成分分析优化后的飞机备件需求预测模型。计算过程如下：

1) 根据影响飞机备件需求的不同因素，收集相关数据，形成备件需求的原始数据集。

2) 对数据进行适用性判别等预处理工作后进行标准化处理，采用主成分分析法对数据进行处理，并选择合适的主成分。

3) 根据筛选出的主成分，选择训练集和测试集。将训练集数据输入岭回归模型进行学习。

4) 采用十折交叉验证方法选择合适的，代入岭回归模型进行学习。采用选取最优的岭回归模型对测试集进行预测，得到相应的预测结果。

基于有偏估计模型的备件需求预测模型的计算流程如图1所示。

4 算例分析

通过对某场站备件保障情况进行分析后得出，影响该型飞机备件需求的影响因素包括以下几个方面。

1) 飞行训练任务。航材备件的消耗与飞行训练任务直接相关，主要的影响因素有飞行时间、起落次数、飞行强度和飞行员技术等因素，一般来说，飞行时间越长，起落次数越多，飞行强度越大，备件消耗量越大，需求也就越大。

2) 飞机备件本身属性。飞机备件的技术状态、产品的质量和生产的工艺等因素都会对备件的消耗产生影响，技术越成熟、器材质量越好，故障率就会越小，备件的需求量也会减小。

3) 自然环境因素。自然环境对飞机备件的技术状态产生较大的影响，其中温湿度对备件的影响最显著，按照保管要求，库房内温度应维持在5～30 ℃，湿度应维持在45%～60%，将温湿度不在该范围的视为异常温湿度[12]。

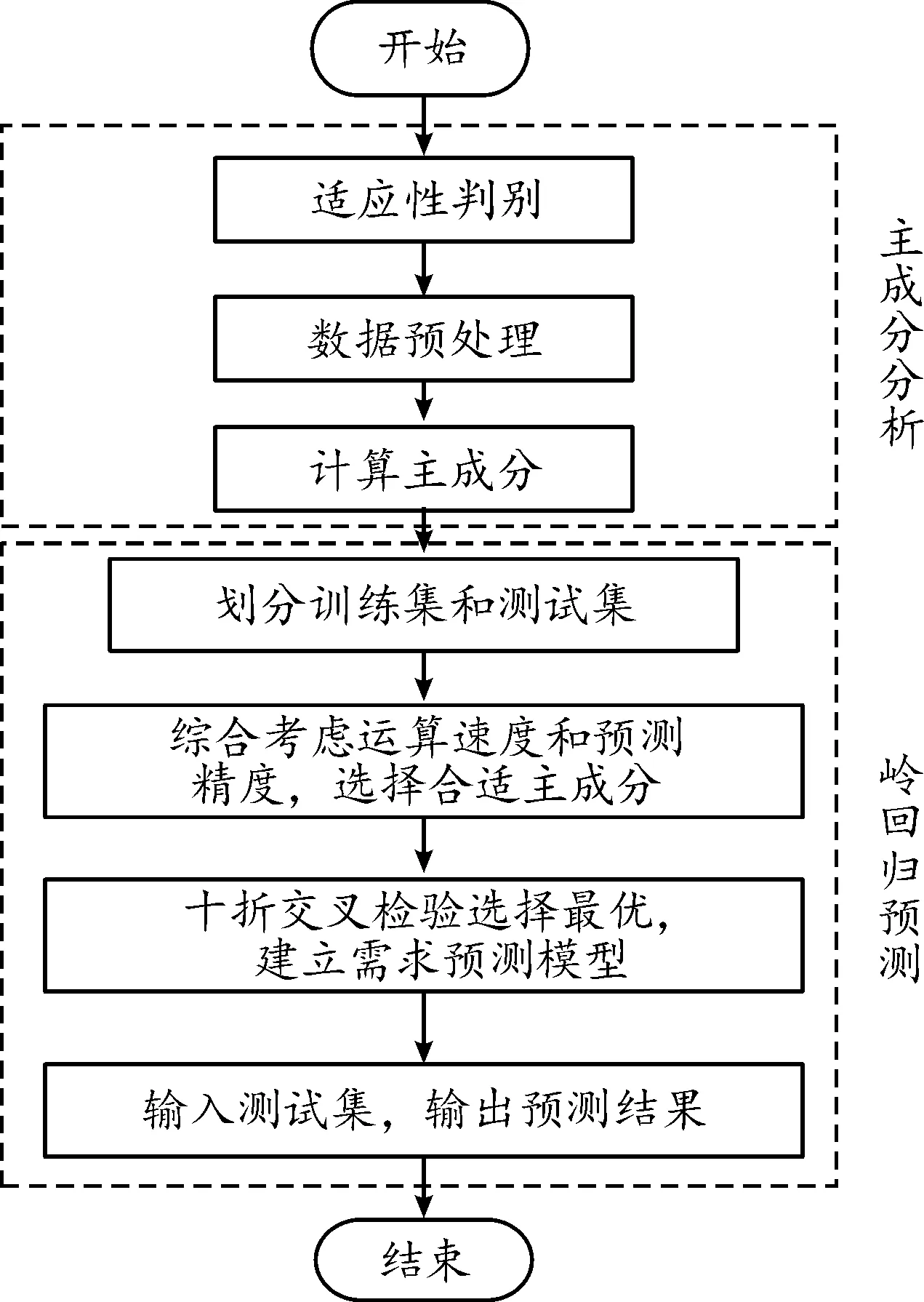
图1 计算流程框图

算例选取发付量Y、飞行时间x1(小时)、飞行起落x2(次数)、操控人员熟练程度x3(百分比)、异常环境温度x4(百分比)、异常环境湿度x5(百分比)、备件故障率x6(百分比)、维修人员技术水平x7(百分比)等7个飞机备件需求量影响因素进行分析，在满足多重共线性需求规律的一次性消耗备件和部分价值较高的可修复备件中随机选取10组数据，算例选取前6组数据为训练样本、后4组数据为测试样本。

4.1 适用性判别

利用最小二乘法和R语言对变量进行线性判别分析得到表1，方差膨胀因子见表2，显著性检验结果如表3所示。

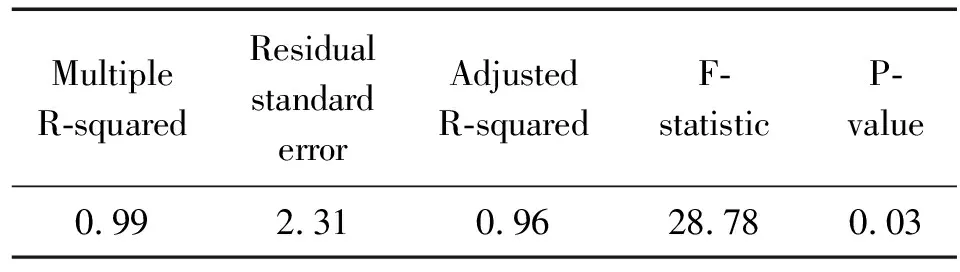
表1 线性判别分析Table 1 Linear discriminant analysis

表2 方差膨胀因子Table 2 Variance expansion factor

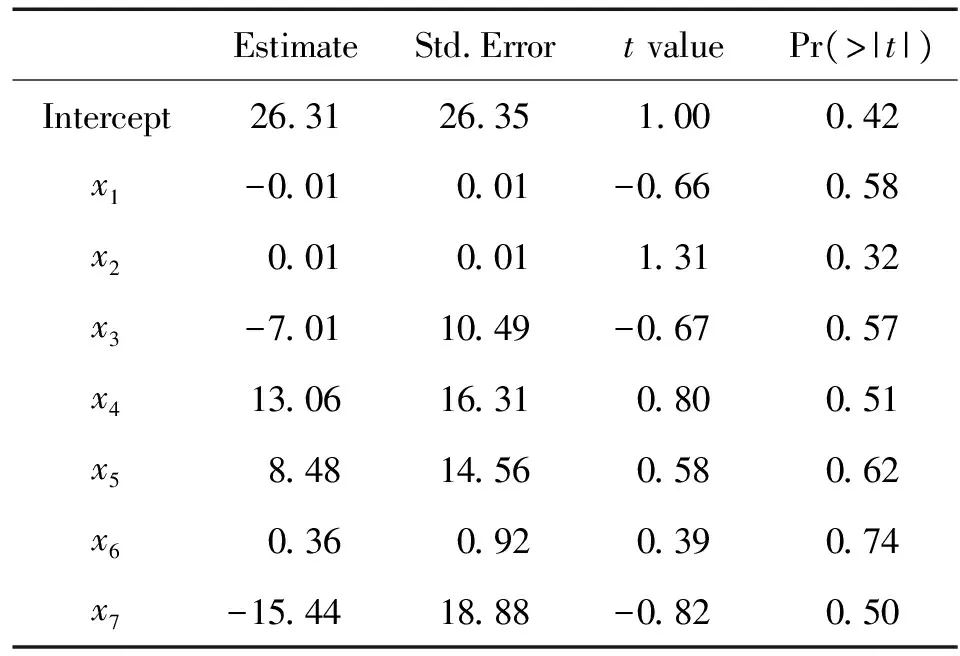
表3 显著性检验结果Table 3 Significance test

由表1和表3可知，Multiple R-squared =0.99和Adjusted R-squared=0.96数值较大，F=28.78通过了显著性检验，总体来说拟合度较好，但在显著性检验时发现，没有变量通过检验且显著性较弱，说明变量不适合用于最小二乘法建模，因此检查变量之间是否存在多重共线性问题。通过R语言car包中的vif函数，利用方差膨胀因子(variance inflation factor，VIF)进行判断，一般认为，vif>5，存在严重的多重共线性问题，由表2可知，变量的方差膨胀因子均大于5，说明变量之间存在多重共线性关系。

利用SPSS软件对数据进行相关性分析，结果如表4所示。

由表4相关系数矩阵可知，变量之间具有很强的相关性，结合方差膨胀因子表明，各项指标之间具有较强的相关性和重叠性，变量之间存在多重共线性，因此适合采用主成分分析法。

4.2 主成分分析和主成分选择

将数据按式(1)标准化处理后得到标准化数据，如表5所示。

利用R语言中的prcomp()函数作为主成分分析工具，将表5数据进行主成分分析，得到各主成分方差解释比例和载荷向量，如表6所示。累计方差解释比率(proportion of variance explained，PVE)如图2所示。

表4 相关系数矩阵元素Table 4 Correlation matrix

表5 标准化数据Table 5 Standardized data

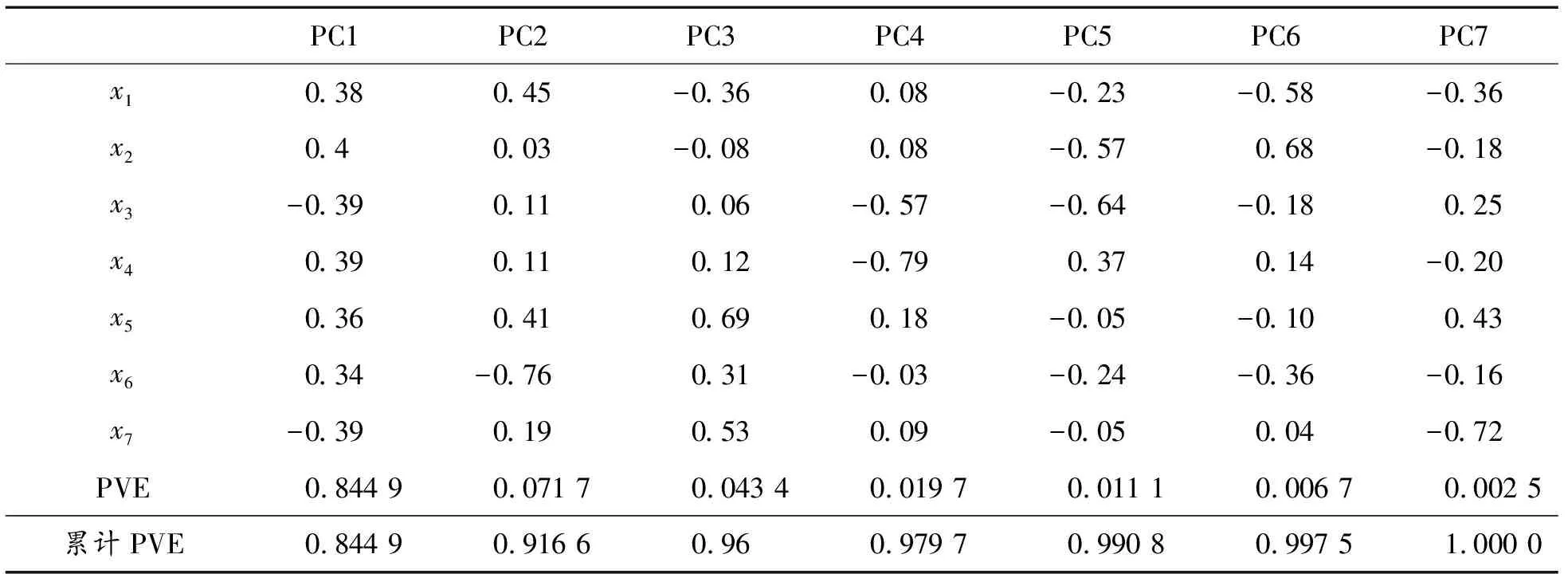
表6 主成分载荷向量和方差解释比率Table 6 Principal component load vector and proportion of variance explained

图2 累计PVE折线

根据表6所得的主成分载荷向量,得到各主成分具体数据，选取前6组的相关数据作为训练集，后4组的相关数据作为测试集，将训练集带入岭回归模型进行学习，运用R语言glmnet包中的cv.glmnet()函数进行十折交叉检验，筛选出最佳值，最后将测试集数据带入模型得到最终预测的结果。根据预测性能综合选择主成分个数，主成分个数和预测结果之间的关系如表7所示。

由表6可知，当主成分选取2个时，累计PVE达到0.916 6，预测效果较好；当主成分个数大于2时，累计PVE虽然有所上升但并不明显，且运算步骤增加导致运算时间增加，预测效果并不乐观，因此综合分析后，算例选择2个主成分作为岭回归的输入变量。

4.3 预测性能分析

为了验证模型预测的可靠性和准确性，采用支持向量回归(support vector regression,SVR)[13]和RBF(radial basis function)核的支持向量机(support vector machine,SVM)[14]进行预测实验对比。算例数据较少，γ和cost的值通过十折交叉检验获得。笔者借助R语言，利用R语言e1071包中的tune()函数获得最佳的γ和cost的值，预测结果比较如表8所示。

表7 预测结果对比Table 7 Comparison of prediction results

表8 模型比较结果Table 8 Model comparison results

根据表8的预测结果可知，对于具有多重共线性关系的变量来说，RBF-SVM的预测效果并不理想；SVR预测效果与有偏估计模型相当，但gamma和cost的选择需要对大量数据进行交叉检验或者利用相关优化算法得到，增加了计算的复杂度且预测精度提高并不明显；与其他模型相比，有偏估计模型的RMSE较小，拟合效果较好，计算简单便捷且预测精度较高，对于处理数据量很大的数据集具有明显的优势。

5 结论

对飞机备件需求进行合理的预测是备件订货的重要一环，根据不同因素综合分析，备件的需求能够使预测结果更加科学准确，从而节省大量的人力物力，提高备件保障的军事效益和经济效益。本文利用有偏估计的思想，首先利用主成分分析法对影响备件需求的多个因素进行分析筛选，有效缩小了数据的规模，降低了数据采集的难度，然后利用岭回归模型进行需求预测，结果表明，有偏估计模型能够很好地解决具有多重共线性关系影响因素的飞机备件需求预测问题，对处理数据量大的数据集具有计算简便、运算速度快等优势，为飞机备件的合理预测提供了一种快速有效的模型。