TIMR:模板图像匹配矫正
2022-05-09张祥祥吕学强游新冬
张祥祥,吕学强,韩 晶,游新冬,张 凯
1(北京信息科技大学 网络文化与数字传播北京市重点实验室,北京100101)
2(首都师范大学 中国语言智能研究中心,北京100048)
1 引 言
随着智能手机、数字相机、手提电脑等移动拍照设备与图像识别的不断发展与应用,外部数字影像信息的获取与智能化分析变得愈发简单与方便化,这为使用移动拍照设备与光学字符识别技术(OCR)对纸质文档数据进行快速的采集、备份、自动化识别与分析等提供了新的方法与途径.
然而,使用移动拍照设备采集的文档图像中文档会因文档的摆放姿态与拍摄的角度产生透视倾斜变形,该变形是文档图像变形中最为常见的变形类型,其在一般的手工拍摄场景下通常难以避免甚至不可避免,这将会对后续的文字与其它内容的检测、OCR识别、文档图像的版面分析等带来困难[1],因此在进行后续的处理之前需要对文档图像进行透视倾斜矫正恢复[2].文档图像透视倾斜变形的矫正普遍采用“四点法”,不同的方法的区别一般在于所使用的获取“四点”的方法不同[3],其通过寻找图像矫正前与矫正后对应的图像文档中的4个角点来达到矫正目的,但如何准确的定位到文档的4个角点并实现通用化的透视倾斜文档图像矫正一直是难以攻克的难点,对此国内外学者进行了一些相关研究.尚新萍等人[4]提出一种基于改进的Hough变换的文档图像倾斜矫正算法,该算法主要针对仅有“旋转变形”的文档图像的矫正,当图像发生“透视变形”时,算法将不再适用,另外该算法需要先验的阈值设定,泛化性差且运行速度较慢;冯雷等人[5]提出一种基于Hough变换与分级倾角检测的优化的文档图像倾斜矫正算法,该算法主要通过缩小Hough变换的角度遍历区间以改善Hough变换运行速度慢的问题,但该算法同样只能矫正“旋转变形”且依赖阈值的先验设定;Abbas等人[6]提出一种基于深度卷积神经网络的文档图像矫正算法,该算法通过对文档的4个角点进行回归实现透视倾斜文档图像的矫正,论文中模型使用合成数据集进行训练,其在合成数据集上效果较好,然而模拟数据集与真实的数据集存在一定的差异,故该模型在实际场景中效果较差,同时其对数据量要求较高,当数据量不足时将不再适用;Javed,K等人[7]提出一种递归调用的卷积神经网络实现文档图像中文档角点的检测与递归化预测修正,并通过预测的角点最终实现文档的矫正,该算法在ICDAR2015会议组织的智能手机文档捕获与识别挑战赛[8]中取得较好结果,但该方法抗干扰性差且同样依赖于大批量的数据训练,不适用背景干扰性大、可用样本少的场景.以上算法虽然理论上可以面向任意领域的文档图像进行矫正,但因为预定的阈值或数据场景分布等问题,以上算法对任意领域的矫正都存在抗干扰性差等问题.
针对以上文档图像矫正现状,本文从图像匹配的角度寻求解决文档图像矫正问题的更佳解决方案,主要的贡献有:1)将领域性透视倾斜文档图像剖离出来进行矫正处理,并引入基于BRISK[9]的图像匹配算法用于透视倾斜变形的领域文档图像矫正,相比之前的传统方法与深度学习方法,具有矫正速度快、矫正效果好、抗干扰性强且无需像深度学习场景下的大批量的训练样本支持等优点;2)针对矫正模板图像检测的无关特征点冗余问题,提出基于先验特征点过滤算法,实现了矫正速度的提升;3)针对矫正模板图像检测的低质量特征点冗余问题,提出迭代匹配过滤算法,从而提炼出高质量的稳定性特征点,进一步提升矫正速度.
2 BRISK特征点检测与描述
2.1 图像尺度空间构建
BRISK算法是Leutenegger S[9]于2011年针对SURF[10]算法特征点检测与匹配速度慢而提出的特征点检测与描述算法.其通过构建多尺度图像金字塔并在各个尺度空间进行特征点检测以保证算法的尺度不变性.其中,BRISK算法的图像尺度空间金字塔由8层组成,包括4层普通图像层与4个内层图像层,分别用ci与di表示(i={0,1,2,…,n-1},n=4).其中普通图像c0为原始图像,普通图像ci由ci-1层2倍下采样生成;内层图像d0由原始图像c0的1.5倍下采样生成,内层图像di由di-1层2倍下采样生成.若用t表示原图像与尺度图像ci与di的相对比例关系,则有:
t(ci)=2i
(1)
t(di)=2i·1.5
(2)
2.2 特征点检测
BRISK算法使用AGAST9-16[11]与FAST5-8[12]进行关键点检测.其中,AGAST9-16应用于图像尺度金字塔的各个尺度层,FAST5-8应用于额外增加的d-1层.通过在图像尺度金字塔的每个尺度上进行检测得出每个特征点及关键的AGAST得分,再对检测出的特征点在相邻的两个尺度空间上使用非极大值抑制以实现强响应关键点的筛选,AGAST得分值为检测的特征点的响应值.由于在图像尺度金字塔的各个尺度层由原图像或采样得到的尺度层采样得来,故在尺度层上检测的特征点的坐标值并非实际图像上的坐标值,因此筛选出的特征点需要通过插值来还原特征点在原图像中的真实位置,如此便可以得到特征点位置.
2.3 构建特征点描述子
BRISK算法的特征点描述子主要有两个关键点:1)是描述子的“二进制”描述[13];2)是描述子的特殊采样模式,前者保证BRISK算法在匹配过程中的高效性,后者保证描述子描述的特征点的旋转不变性[14].BRISK算法的描述子由图像特征点邻域精心设定的不同点位的亮度对比结果构成的二进制字符串组成.由于BRISK描述符的“二进制性”描述,不同图像特征点描述符的距离可以使用位运算进行计算,这种描述方法保证BRISK算法在匹配过程中的高效性.BRISK的采样模式为N=60采样,把N个采样点任意的两个不同采样点Pi与Pj分别两两组合得到N(N-1)/2个采样点对集,将该集合用A表示,则该集合可以表示为:
A={(Pi,Pj)∈R2×R2|i≤N,j (3) 其中,(Pi,Pj)表示Pi与Pj构成的采样点对.若将g(Pi,Pj)表示为采样点对的局部梯度集合,I(Pi,σi)与I(Pj,σj)分别表示高斯滤波后的采样点,则有: (4) 记δ为采样点对之间的距离,分别设定特定的距离阈值δS,δL,从点对集合A中划分出短距离点对子集S与长距离点对子集L,则两者可以表示为: S={(Pi,Pj)∈A|‖Pi-Pj‖<δS} (5) L={(Pi,Pj)∈A|‖Pi-Pj‖<δL} (6) 其中,δS,δL分别取值为9.75t与13.67t;t为特征点所对应的尺度比例值. BRISK算法使用长距离子集L计算特征点的方向,计算公式如公式(7)所示: (7) 其中,g是特征点的主方向;gx,gy分别为长距离点对子集L中各个采样点对在两坐标轴x与y方向上的梯度;l为子集L中所有采样点对之间的距离的和.在生成特征点描述子之前,为保证方向不变性,还需要将采样模板沿着中心顺时针旋转θ度,其中θ为: θ=tan-1(gy,gx) (8) 采样模板旋转后,再通过对比短距离子集S中采样点对对应的图像点的灰度值,最终生成二进制描述子.比对方法如公式(9)所示: (9) 模板图像匹配矫正算法主要分为5步,如图1(a)所示.具体流程的细节原理如下: 图1 算法流程图Fig.1 Algorithm flow chart 3.1.1 矫正模板图像制作 选取一张领域内的透视倾斜文档图像,通过交互式选取其4个顶点,通过透视变换将其矫正得到文档图像的正向平行视图图像,记该正向平行矫正模板文档图像为IT. 3.1.2 特征点检测与描述 将矫正模板图像与待矫正文档图像输入BRISK算法中进行特征点检测.若将BRISK特征点检测器的检测过程用P,D=fBRISK(I)表示,则其输入为图像I、输出为检测出的特征点坐标序列P与相应的特征点描述子序列D.记正向文档图像为IT、待矫正文档图像为IR,并记两者经过BRISK算法得到的特征点序列与描述子序列分别为PT、DT与PR、DR,则两者的特征点检测过程可由公式(10)与公式(11)表示. PT,DT=fBRISK(IT) (10) PR,DR=fBRISK(IR) (11) 3.1.3 特征点匹配 两幅图像特征点的匹配即为两幅图像特征点对应的描述符的匹配.本文使用简单方便的暴力(Brutal Force,BF)匹配实现BRISK特征描述子的匹配,若将特征点暴力匹配算法记为函数PPair12=fBF(P1,D1,P2,D2),则其输入为两幅图像的特征点P1、P2与对应的特征点描述子D1,D2,输出为成对的特征点序列PPair12.若矫正模板图像与待矫正文档图像之间匹配的特征点对序列为PPairTR,则PPairTR可由公式(12)表示.其中本文采用汉明距离进行特征点距离计算,则输入的两个特征点描述符序列单元的不同值的数量即为两个不同特征点的距离.若dT与dR为正向文档图像与待矫正文档图像的两个描述子,又因为BRISK算法的描述子数量为n=512,则两者的汉明距离可由公式(13)表示: PPairTR=fBF(PT,DT,PR,DR) (12) (13) 其中,⊕表示异或运算. 3.1.4 单应矩阵估计 单应矩阵表示同一平面在不同视角投影下的变换关系[15],其反应了两个视角投影下的相同点的一一对应关系.设矫正模板图像上的一点Pt坐标为(xt,yt)、与Pt相对应的待矫正文档图像的一点Pr的坐标为(xr,yr),并设Pr变换到Pt的单应变换矩阵为Hr2t,Hr2t可由公式(14)表示,则在齐次坐标下Pr到Pt的透视变换关系可以由公式(15)表示,消去齐次坐标项可得公式(16),整理后可以得到矩阵形式如公式(17)所示.由于单应矩阵具有8个未知参数,则求解单应矩阵各个参数的值就至少需要8个线性方程组,又因为图像上的一对匹配坐标点的坐标代入公式(17)可以构成两个线性方程,故至少需要4对相匹配坐标点才可求解单应矩阵.本文采用RANSAC算法进行单应矩阵的求解,以不断循环迭代的方式,从包含异常或误差样本的数据样本中随机选出一部分样本数据进行模型参数估计,最终找出符合正常样本个数最多、误差最小的模型参数,其中这里的包含误差的样本即为特征点的匹配结果PPairTR,模型参数即为Hr2t.若将RANSAC算法用H=fRANSAC(PPair)表示,则Hr2t可由公式(18)表示. (14) (15) (16) (17) Hr2t=fRANSAC(PPairTR) (18) 3.1.5 文档图像矫正 求得单应矩阵Hr2t后,即得到待矫正文档图像IR到正向文档图像IT的坐标变换关系,要求得矫正结果图像即需要对待矫正文档图像IR的每一个像素进行单应变换,而矫正结果即为每个像素单应变换后的集合,若记矫正结果图像为IR2T,IR的宽高为wR与hR,则IR2T可以由公式(19)表示. (19) 由于BRISK特征点广泛且大量存在,所以基于BRISK算法的图像匹配具有较高的匹配精度与匹配可靠性[9],其可以保证TIMR算法矫正效果的高精度性,但与之相对的广泛且大量的特征点之间的逐一匹配也会使算法实时性变差[16],而由3.1.4可知TIMR算法中只要保证有4个高质量的匹配点就可以保证较好的匹配与矫正效果.因此,对检测的特征点进行一定数量的过滤可以在保证匹配与矫正的精度的同时提升算法的实时性. 基于以上分析,本文提出特征点先验过滤与迭代匹配过滤实现TIMR算法中矫正模板图像的特征点的过滤以实现算法实时性的改善.特征点过滤优化后的TIMR算法流程图如图1(b)所示,具体算法原理与分析如下: 3.2.1 特征点先验过滤 TIMR算法主要针对特定领域的文档图像的矫正,而领域性文档图像中存在不变的文字或图像内容,这些不变的内容区域所检测出的特征点一般会稳定性存在,即在理想的尺度不变、旋转不变、色彩不变等情况对该特定领域的任意的文档图像进行特征点检测时均会检测出相同的特征点,这些稳定存在的特征点保证了TIMR算法的可行性;而相对就有变化的文字或图像内容,这些区域一般为文档的个性化内容区域,其一般为文档使用者个人信息相关联的内容,如使用者需要自己填写或者随使用者信息打印的姓名、性别与日期等内容,这些内容会随着文档使用者的不同而不同,因此这些区域检测出的特征点在进行匹配时一般得不到正确的匹配结果,同时还会影响算法的实时性. 综上所述,对文档图像非稳定性特征点的过滤是非常必要的.为提升TIMR算法的实时性,本文提出特征点先验过滤(Prior Filtering,PF)对矫正模板图像的特征点进行过滤优化从而实现算法的加速,具体处理方法如下:首先,将文档图像的矫正模板图像中稳定不变区域进行矩形框选标注,获取由多个矩形框内部坐标点构成的图像点集,记该点集为PBBOX,若标注的边框数量为NBBOX,第i个边框的左上角坐标与宽高为(xi,yi,wi,hi),则PBBOX可由公式(20)表示;然后将得到的点集PBBOX与BRISK检测得到的特征点集PBRISK-t进行集合间的交运算得到两者的公共点集,该公共点集即为先验过滤后的特征点点集,记该点集为PPF,则先验过滤后的特征点点集PPF可以由公式(21)表示. (20) PPF=PBRISK-t∩PBBOX (21) 3.2.2 特征点迭代匹配过滤 BRISK算法的特征点具有较强的稳定性,但目前的图像一般均为横向与竖向的等距排布栅格影像,其本质为具有一定采样距离的二维离散信号,因此,其是离散的,也正因为图像的离散型性,任何的特征点检测算法检测的特征点都不具有完全的、绝对的稳定性;所以即使是文档图像中的不变的稳定性区域依然存在冗余的不稳定的特征点,因此,对这些不稳定的特征点的进一步过滤是非常有必要的. 基于以上分析,本文提出迭代匹配过滤算法(Iterative Matching Filtering,IMF)实现非稳定性特征点过滤,详细过程如下:首先获取一定数量的不同角度与不同环境下的透视变形文档图像,然后对每一张图像进行遍历,对遍历的每一张图像进行特征点检测,并将检测得到的特征点与前面先验过滤后的特征点进行匹配,匹配正确的特征点保留,匹配错误的特征点过滤,每次循环过滤后保留的特征点作为下一次迭代匹配过滤的输入,当循环遍历完所有图像时保留的特征点即为在不同角度不同光照环境下筛选过滤的最终的稳定的性特征点.若记用于迭代匹配过滤的文档图像数量为NIMF,记第i次输入的文档图像为IIMF(i)、第i次匹配时正确匹配的模板文档图像特征点集合为PIMF(i)(i=1,2,…,NIMF),并将每次的匹配过滤的过程用函数fIMF表示,则fIMF函数的输入为上一次的匹配正确的模板特征点点集与新输入的文档图像检测出的特征点集合,其中第一次输入的匹配正确的模板特征点为上一节边框过滤后的特征点,即PIMF(1)=PPF,则迭代匹配过滤可用公式(22)表示. PIMF(i+1)=fIMF(PIMF(i),fBRISK(IIMF(i))) (22) 实验集数据由某医疗公司提供的来自不同检验者、不同检验项目的真实检验单在自然环境下人工拍摄而成,采用的拍摄设备为型号为vivo U3x的智能手机.为保证数据的多样性,拍摄时在保证文档内容尽可能完整且内容可人工分辨的前提下采取随机的背景、随机的摆放角度、随机的拍摄角度、随机的拍摄距离以及随机的自然光照环境,最终拍摄的文档图像数据集共计41张,尺寸为4160×3120或3120×4160像素.根据实验需求将该数据集随机划分为3部分,具体细节如表1所示.图2显示了该文档图像数据集下的4张图像样例.特别地,为了方便实验结果的量化分析,我们对第3部分中的文档图像做了角点坐标标注. 表1 数据集划分与用途描述Table 1 Data set partition and usage description 图2 数据集中的部分图像样例Fig.2 Some image samples in the dataset 文档图像矫正一般应用于纸质文档的扫描与识别等处理,其一般对矫正的效果要求较高,同时在一定的场景下要求一定的实时性.良好的矫正效果可以方便对扫描文档的进一步处理与分析,实时性处理可以在实际应用中带来良好的交互体验.因此,本文从矫正效果与矫正速度两方面对本文所提算法进行评估. (23) 本文的所有实验均在个人PC上进行,实验的基本环境如表2所示. 表2 实验环境Table 2 Experimental environment 在进行实验之前必须先制作一张矫正模板图像,这是TIMR算法的关键一步.此处使用数据集第1部分的单张透视倾斜变形文档图像进行制作,选取变形文档图像的4个角点通过透视变换得到矫正模板图像.其中,用于制作矫正模板的原图与标注如图3(a)所示,制作好的矫正模板图像如图3(b)所示.其中,论文中涉及隐私的图例我们做了掩码处理. 图3 正向矫正模板图像制作Fig.3 Positive rectification template image making 4.3.1 特征点过滤实验 矫正模板特征点过滤包括两个阶段:1)个是特征点先验过滤(Prior Filtering,PF);2)另一个是特征点迭代匹配过滤(Iterative Matching Filtering,IMF).两个阶段的过滤旨在实现算法的加速,PF过滤的为与“矫正无关”的特征点,其可以实现算法的提速且不会影响算法精度,而IMF为“矫正相关”的稳定性特征点过滤,其在实现算法提速的同时需要验证特征点的过滤是否会影响算法的矫正精度.因此,本文在对特征点过滤前后的算法速度进行对比的同时也对过滤前后的矫正精度进行了对比,详情如图4-图6所示. PF为特征点过滤的第1阶段,过滤前后的相关指标变化由图4-图6中第1条竖直虚线左侧所示.由图4可知,经过PF后特征点数量发生骤降,由7215个特征点下降到4208个特征点,数量下降了3007个,占总数量的41.68%;又由图5可知经过PF后算法的矫正用时从平均2.21秒一张下降到1.74秒一张,实现了平均0.47秒的速度提升,速度提升比例约21.27%;同时再由图6可知经过PF后算法的矫正精度呈现较稳定地状态.因此,PF可以通过过滤掉矫正模板中的无关特征点实现不损失矫正精度的同时提升算法矫正速度,这也验证了上文的分析. 图4 矫正模板图像特征点数量随特征点过滤次数的变化Fig.4 Number of key points of rectification template image varying with the filtering times of key points图5 算法用时随特征点过滤次数的变化Fig.5 Algorithm time varying with the filtering times of key points图6 平均矫正精度随特征点过滤次数的变化Fig.6 Average rectification accuracy varying with the filtering times of key points IMF为衔接PF的第2阶段特征点过滤,每次迭代过滤前后的相关指标由图4-图6中第1条竖直虚线右侧所示.由图4可知,经过第1次与第2次IMF后特征点数量发生大比例的下降,特征点数量由4208下降到351个,两次过滤特征点下降的比例达到了91.66%,这说明BRISK特征点中存在大量稳定性弱的特征点,而第3次-第10次IMF后,特征点的数量降低程度不再明显,这说明了由BRISK特征点存在稳定性差异,并且IMF能够有效筛选出其中稳定性足够强的特征点.再由图5可知,算法的整体矫正用时与中间各个部分的用时的下降趋势与特征点数量下降的趋势相近,均为先骤降在逐渐变缓,这说明特征点数量与算法的速度成一定的正相关关系.结合图6可知,第1次-第5次IMF过程中,算法的矫正精度有细微的波动,但均保持在39个像素之内(MDEIMF4=38.63 pixel<39 pixel)且最大像素波动值保持在6个像素以内(MDEIMF4-MDEPF1=5.79 pixel<6pixel),这样的误差相比较于4160×3120或3120×4160像素的测试集文档图像而言可以说微乎其微,基本不影响矫正效果,而在迭代匹配的第6次-第10次,矫正精度在测试集上呈现出稍大且不可忽略的波动,这间接地验证了特征点的稳定性不是绝对的,对特征点的过滤需要在改善算法效率的同时且保证矫正精度的情况下进行.因此,综合矫正效率与算法稳定性,本文采用第5次迭代匹配过滤的结果作为矫正模板. 经过两阶段的过滤,特征点数量由7215下降到209,总体减少了97.10%,图7中3幅图展示了两阶段过滤前后特征点由稠密到稀疏的变化,图中“+”形符号表示检测到的特征点;矫正速度由平均2.18秒下降到平均1.20秒,提升了44.95%;而矫正精度又可以保持在可以忽略的范围之内,图8展示了经过两阶段过滤后的特征点匹配可视化结果与良好的矫正结果.这说明了特征点过滤可以在保证良好的矫正效果的情况下优化算法速度.其中过滤前后TIMR算法的各项指标汇总后如表3所示. 图7 特征点过滤变化对比图Fig.7 Comparison chart of feature point filtering varying 表3 特征点过滤前后各项指标对比Table 3 Comparison of each index before and after key point filtering 图8 特征点匹配与矫正Fig.8 Key point matching and rectification 4.3.2 矫正精度与速度对比实验 为验证本文所提算法的有效性,本文以当前的主流的商业文档图像处理软件(CamScanner(1)https://www.camscanner.com/与ABBYYFineReader(2)https://www.abbyy.com/)与主流的深度学习算法(文献[6]中算法与文献[7]中算法)进行对比.矫正精度与速度的对比验证仍采用算法预测的文档角点坐标与真实坐标的平均绝对误差(MDE)与平均每张文档图像的矫正时间,同时对矫正成功的数量与正向性矫正结果数量进行统计,相关的对比结果如表4所示,各种算法的文档角点预测结果与矫正结果对比如表5所示. 表4 矫正效果对比Table 4 Comparison of rectification effect 由表4可知,本文算法在矫正精度、矫正成功数量、正向性矫正结果数量均远远优于其它算法;对于算法速度,本文算法虽未达到最优,但亦保持了一个可观的结果.再结合表5,可知其它各种算法对文档背景简单(如表5中Image1)的情况下可以实现可观的矫正效果,在复杂的背景(如表5中Image2)的情况下则矫正效果较差,在文档缺角(如表5中的Image3)的情况下只有ABBYY FineReader有较好的矫正效果,而本文算法在以上各种情况下均有良好的矫正效果.综上,可知本文算法在矫正效果上最好,具有矫正效果好抗干扰性强可实现正向性矫正结果等优点. 表5 算法矫正效果对比Table 5 Comparison of algorithm rectification effect 本文根据当前文档图像矫正的现状将领域性文档图像单独剖离出来处理,引入BRISK图像匹配算法对透视倾斜文档图像进行矫正,提出模板图像匹配矫正算法,同时将BRISK算法在矫正模板图像上的检测的冗余与高质量特征点进行过滤优化,并在某医疗公司的真实检验单图像数据集上进行测试、与主流商业软件和深度学习方法对比.实验结果表明,模板图像匹配矫正算法使用简单便捷、矫正速度快、矫正效果好、抗干扰性强且能够有效避免当文档图像倾斜角较大时引起的矫正文档图像侧立或倒立的情况,可以有效胜任领域性的文档图像矫正任务.3 模板图像匹配矫正算法
3.1 算法基本原理与流程

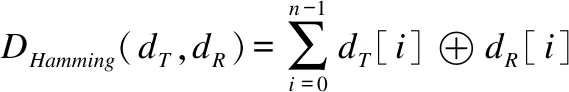
3.2 特征点过滤优化
(i=1,2,…,NIMF)4 实验与分析
4.1 数据集准备


4.2 算法评估标准

4.3 具体实验

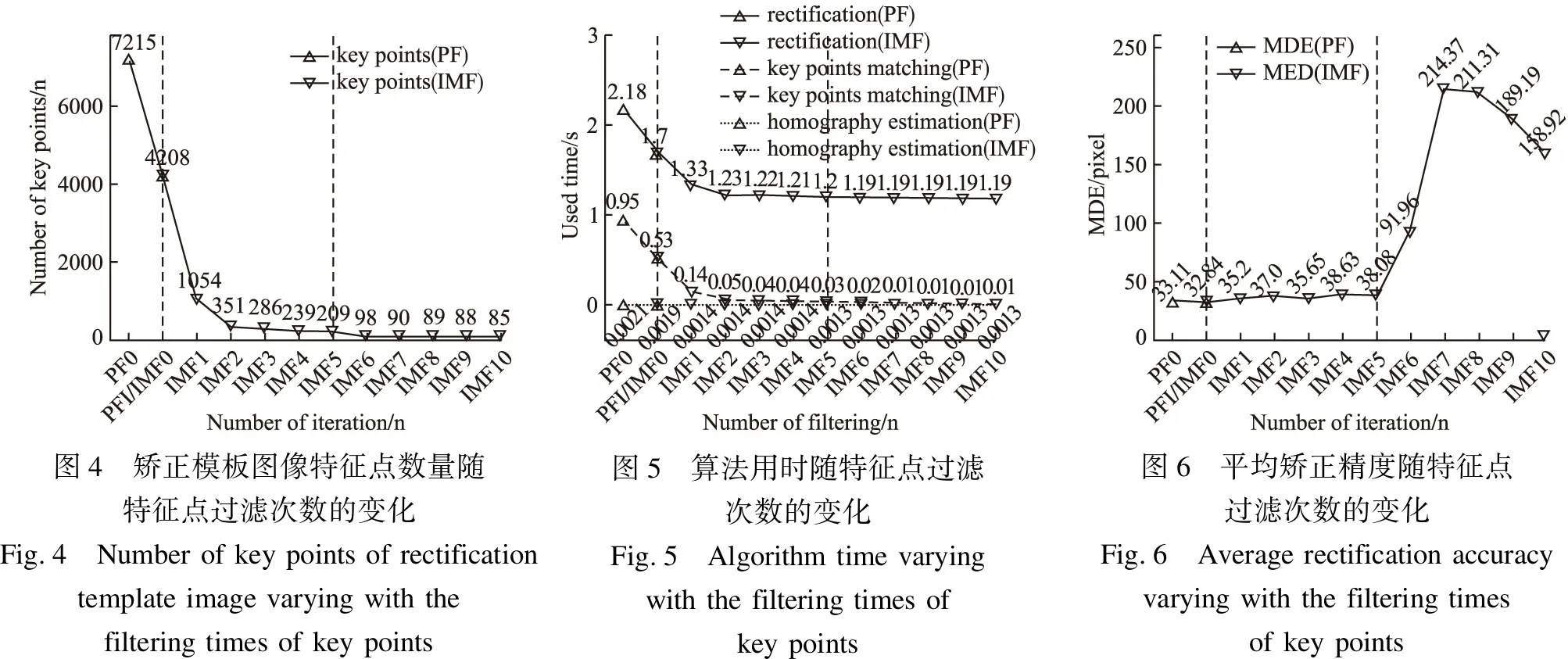





5 结束语
