深孔台阶爆破振动衰减及信号能量频域分布特征

王进忠 年鑫喆

（1.固原市公安局经济开发区分局；2.陕西中爆检测检验有限责任公司）

某露天煤矿所处区域山势较陡，沟谷发育，为典型的山区地形地貌特征。采用露天剥离方式采煤，从矿区的东北角开始，分层次、台阶、区域向南和西方向推进爆破。岩性为石英砂岩与灰黑色页岩，呈不等厚互层。该煤矿采用露天深孔爆破方式进行剥离，爆破区域周围一定范围内存在铁路桥梁、矿区房屋等保护目标，爆破振动可能对这些保护目标产生不利影响。为分析该煤矿露天爆破振动速度和频率随水平距离和高程变化的衰减规律，进行了5次爆破振动测试。通过对测试数据进行分析，探究该区域露天爆破振动衰减的特点及爆破振动信号能量频域分布的特征，为爆破设计优化工作提供依据［1-3］。

1 测试方案

研究表明，露天台阶爆破振动存在高程放大效应，也有学者提出考虑高程放大效应的振动计算公式，但由于爆破振动受各地域岩土介质性质和地质构造影响显著，故需要通过爆破振动测试获取振动数据，有针对性地分析某个区域的爆破振动衰减特性。

测试选在煤矿爆区西侧相邻的台阶地面上。测试分2 种类型，类型1 是底部台阶爆破时，测试上部不同高程的台阶前沿地面的振速；类型2是底部台阶爆破时，测试上部某一高程台阶内侧不同距离处地面的振速。测试时测振仪同时采集地表面3 个相互垂直方向的振速分量及主振频率，数据分析时在3个方向中选取最大值作为该点的振速。传感器布设时，用石膏粉加水调配后涂抹在测振仪底部，将测振仪与地面连接，在保证测振仪水平的同时，测振仪径向大致朝向爆心位置。待爆破完毕后人工收回测振仪，读取数据进一步分析。

测试采用的智能网络测振仪是基于物联网技术研制的，该型测振仪设置简便，具有体积小、重量轻、抗冲击的特点，具备自动连续监测等功能。同时，测振仪标定信息和测试数据均上传云服务系统保存，便于后期分析。

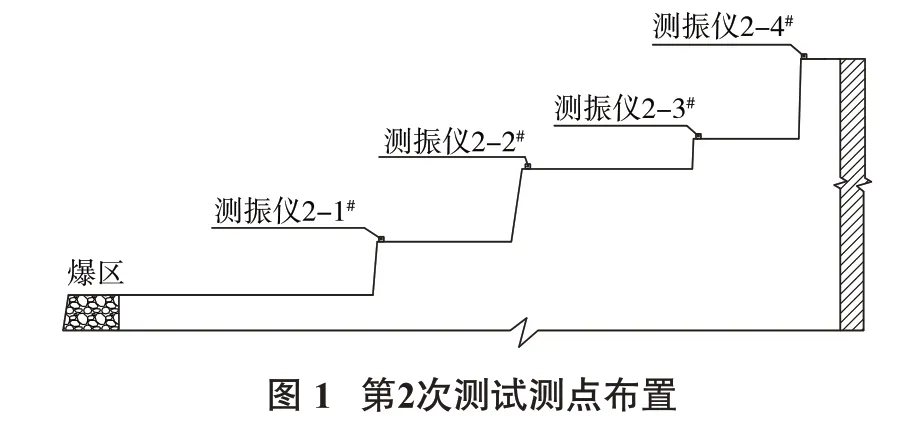
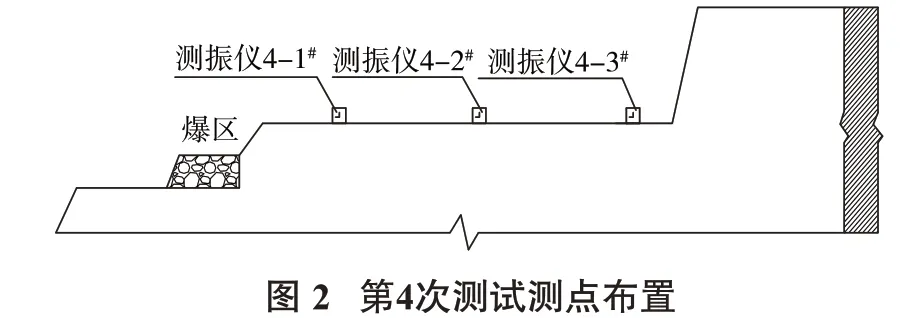
主要测试参数设置如下：第1次测试采样频率为1 875 Hz；第2～5 次测试采样频率为4 687 Hz；触发电平为3%。测试具体安排见表1。第2、4 次测试的测点布置分别如图1、图2所示。

2 测试结果分析

2.1 测试数据

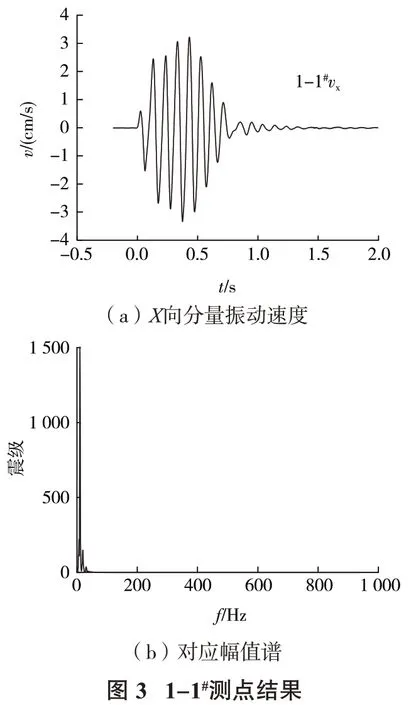
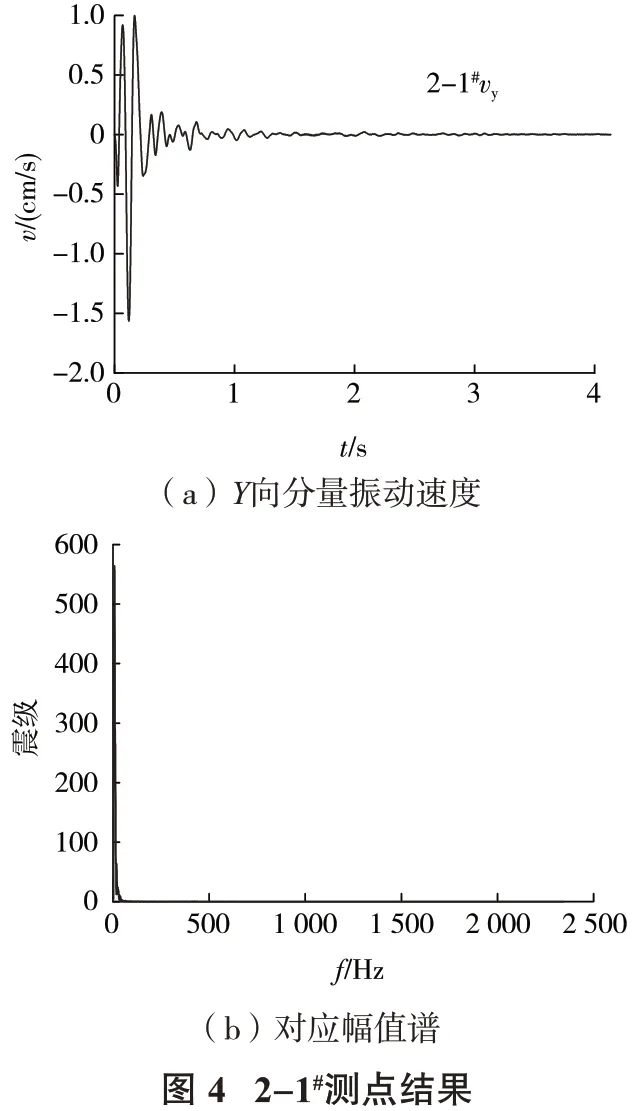
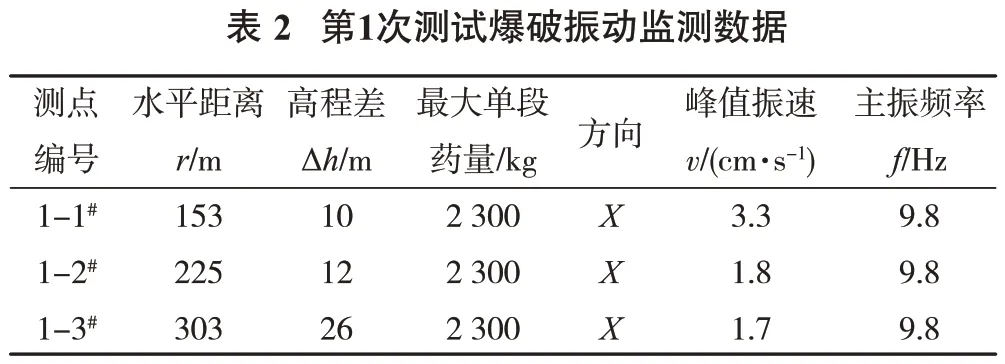
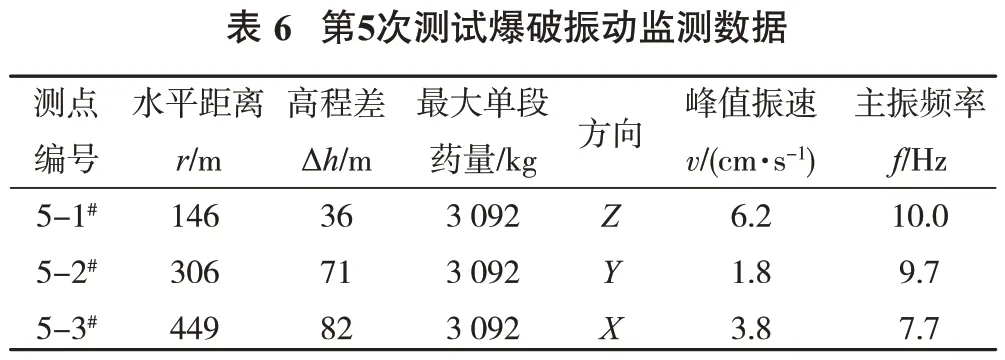
在三向振动速度中，取最大的峰值振动速度及其对应的主振频率。图3、图4 分别为1-1#，2-1#测点处测到的爆破振动速度信号及对应的傅里叶谱。爆破振动测试数据见表2～表6。

2.2 主振频率分析

在大部分测点处，地表质点峰值振速对应的方向主要为水平径向（X向）或水平切向（Y向）。主振频率大致在7～10 Hz。

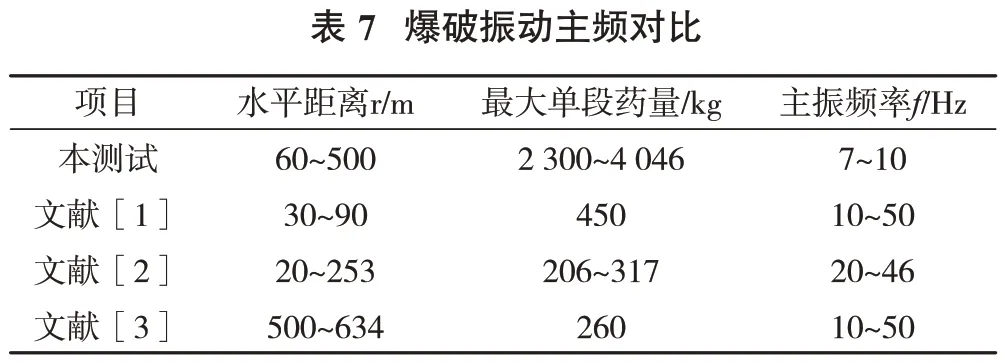
针对露天深孔爆破振动对应的主振频率，将本测试结果与部分露天矿爆破振动监测结果进行对比，见表7。

由表7 看出，本次测试到的振动主频相对低一些，主要是由于本测试的最大单段药量大，为其他爆破的5～10倍，所以产生的振动主频更低。

2.3 振动衰减分析

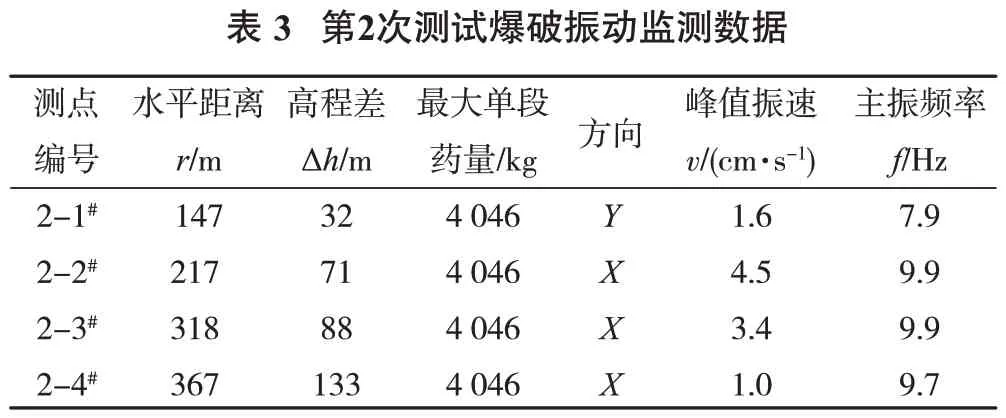
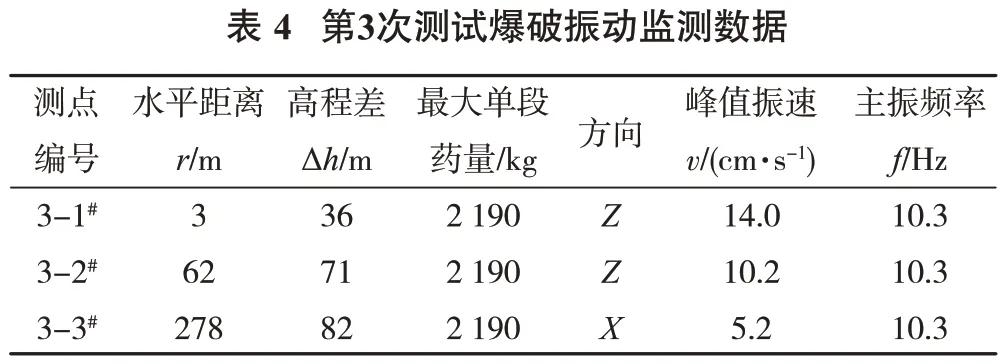
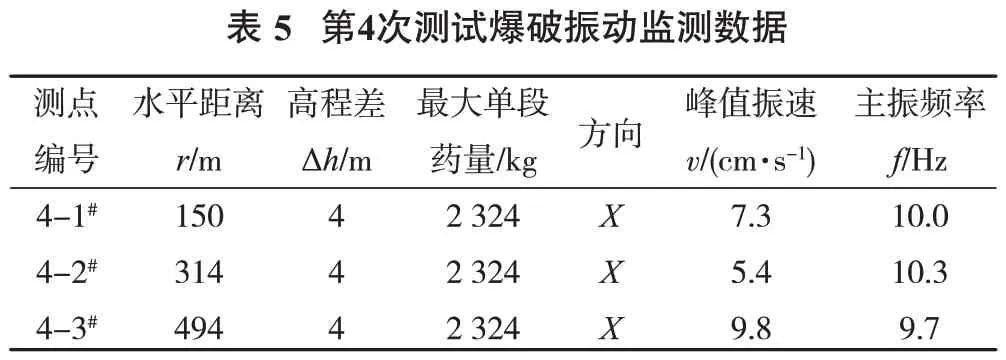
张志毅等［4］根据安托山深孔爆破的振动监测数据，推导分析得到加入台阶高程变化的爆破振动速度计算公式：

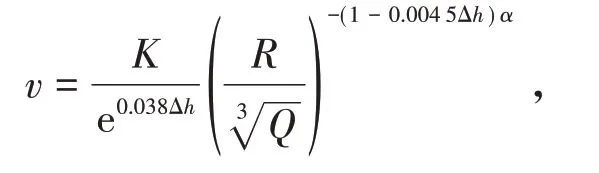
式中，v为振动速度峰值，cm/s；R为测点至爆破点之间的水平距离，m；Q为炸药质量，齐发爆破为总药量，延时爆破为最大单段药量，kg；K，α为与爆破点至保护对象间的介质性质、地形、地质条件有关的系数和衰减指数；Δh为测点与爆心的高程差，m。

结合施工区域岩性和地质条件，取K=300，α=1.8，由公式可计算出不同高程台阶地面振速。在各次测试得到的爆破振动速度相互垂直的三向分量中选取最大分量，与公式计算值对比见图5，图中表示测点距爆区的水平比例距离。

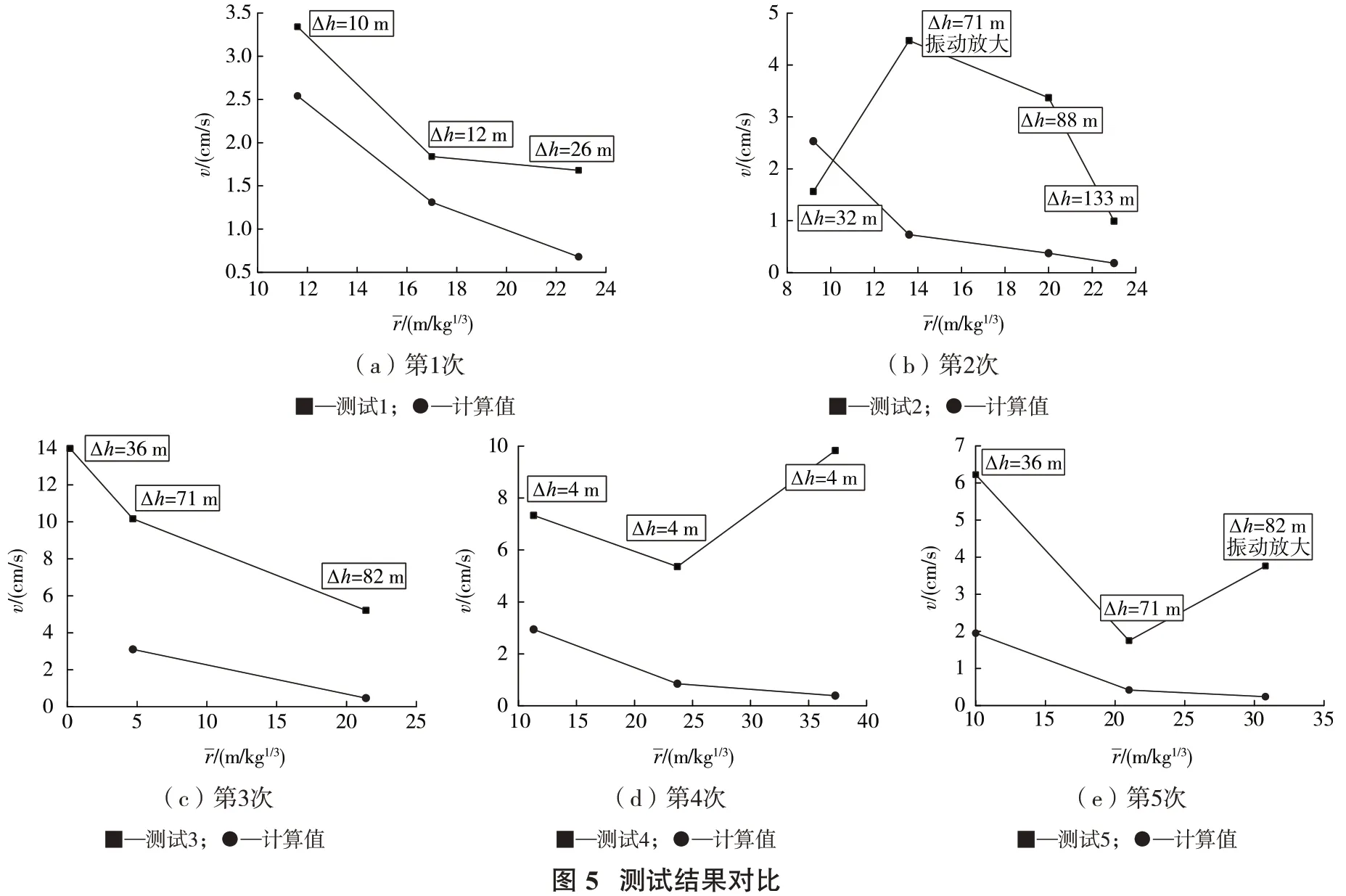
第1次测试测点布置在同一台阶地面上，由于台阶面具有一定倾斜度，每个测点高程不一样。由图5（a）看出，同一台阶地面振速随爆心距和高程的增加衰减，台阶与爆区的高差由10 m 增加至12 m，测得的振速衰减趋势与公式计算结果基本一致，高差由12 m增加至26 m，测得的振速衰减相比公式计算结果变慢。总体而言，在高程逐渐增加的同一台阶地面上，振动速度是逐渐衰减的。

第2、3、5 次测试测振仪布置在不同高程的台阶前沿地面上。由第2 次测试结果（图5（b））可知，2 个台阶（Δh=71 m，Δh=88 m）前沿振速明显大于下一台阶（Δh=32 m）前沿振速，随着台阶高度增加，2个台阶（Δh=88 m，Δh=133 m）前沿振速减小。由第5 次测试结果（图5（e））可看出，Δh=71 m 台阶前沿振速小于Δh=36 m 台阶前沿振速，Δh=82 m 台阶前沿振速又明显大于Δh=71 m台阶前沿振速。

对比公式计算结果，台阶地面振速随水平距离和台阶高程增加而减小。测试结果与公式结果存在差异，这是因为露天爆破台阶前沿地面振速并不一定随爆心水平距离和台阶高程增加而衰减。这2 次测试结果反映出台阶存在爆破振动的高程放大效应。这种效应产生的原因一方面是台阶相比主体边坡是突出的结构，其自身质量、刚度较小，自振频率比主体边坡大，当收到外界激励作用时，相对主体边坡容易产生更大的振动速度，这称作“鞭稍效应”［5-7］；另一方面，公式由不同高程台阶地面振动速度数据回归分析得出，在回归时未采用台阶前沿附近的振速。

第3 次测试结果对比如图5（c）所示，可看出，不同高程台阶前沿地面振动速度随高程增加逐渐衰减，并未体现出高程放大效应。高差由71 m 增加至82 m，振动速度减小趋势与式（1）结果相似，测试结果数值更大一些。Δh=36 m 台阶前沿测点距爆区水平距离为3 m，式（1）计算结果与实测值偏差较大，故未列出。

第4次测试测点布置在同一高程台阶面上，各测点高程一致。由图5（d）看出，距爆区最远处的测点处振速相比另外2个测点处振速显著增大，与公式计算结果变化趋势不一致。具体原因还需要进一步分析。

以上每次的测试结果都有一些特点，但由于测试次数和数据量比较少，还不能体现出宏观的统计规律。公式计算结果仅作为振动衰减趋势的参照。今后将继续开展监测，获得足够的数据，更进一步开展数据统计分析。

2.4 振动信号能量频域分布特征

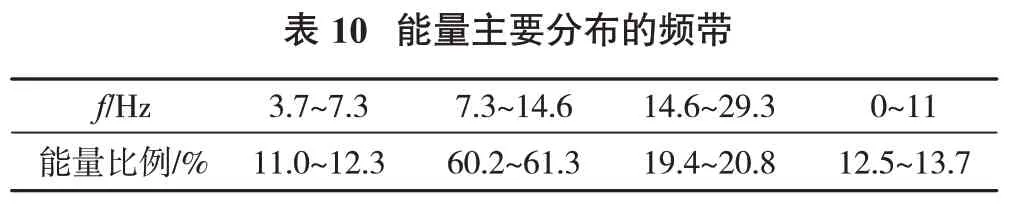
运用小波包［8-10］将5 次测试到的爆破振动信号（分别对应于表2～表6）能量进行频带分解，分解层数为9，得到各爆破振动信号能量比例在不同频带的分布。第1 次测试信号的频带划分见表8，第2～5 次测试信号的频带划分见表9。

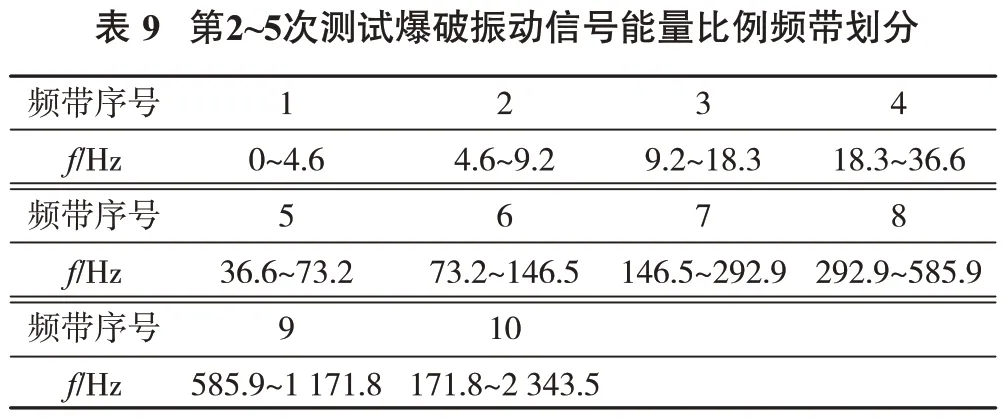
图6 为各次测试到的爆破振动速度能量频域分布，频带序号与表8和表9对应。

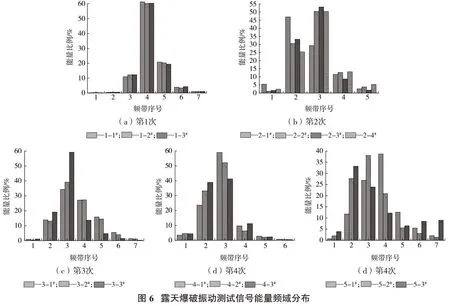
经过统计，测试信号能量主要分布的频带见表10。其中11 Hz 以下分量对应的能量比例由爆破振动信号中0～11 Hz 各子频带对应的能量比例进行累加得到。

由表10 可知，深孔爆破振动速度信号能量主要分布在7.3～14.6 Hz和14.6～29.3 Hz这2个频带，11 Hz以下的成分对应的能量比例较少，为12.5%～13.7%。

3 结论

（1）露天台阶爆破振动存在明显的高程放大效应，即“鞭稍效应”。

（2）在大部分测点处，地表质点振动相互垂直的3 个分量中，水平径向（X向）及水平切向（Y向）的分量值比垂向（Z向）分量值大一些。主振频率大致在7～10 Hz。

（3）露天深孔爆破振动速度信号能量主要分布在7.3～14.6 Hz 和14.6～29.3 Hz 这2 个频带，对应分量能量占总能量的比例分别为60.2%～61.3%和19.4%～20.8%，11 Hz 以下分量对应的能量比例较少，为12.5%～13.7%。