对一道积分极限题目的推广
2022-05-07文韵涵庞学诚
文韵涵, 庞学诚
(华东师范大学 数学科学学院,上海200241)
1 引 言
对一道求积分极限的题目(来源于“中国数学分析交流平台”)进行分析并推广,得到了对斯特林公式的一种新证明.
在证明下面引理的基础上,对一道第九届全国大学生竞赛题给出不同的证明方法.
证因为f在[0,1]上严格单调增,所以x=1 处取得最大值.故f′(1)≥0,下分两种情况讨论,将f在x=1 处泰勒展开
f(x)=f(1)+f′(1)(x-1)+o(x-1)=1+f′(1)(x-1) (x→1-),
(i)当f′(1)>0时,取任意 0<δ<1,则

令

因为在[0,1-δ]上有
0 故 取任意 0<α≤f′(1)≤β,则 经计算 所以 综上,有 注 引理1中f严格单调递增只是为了保证f在[0,1]上的最大值点唯一.此外,本题是对最大值点在区间右端点的情况进行讨论,实际上对区间左端点也可以得到类似结论,若为区间内点,则f在这点的一阶导数必为0,从而极限趋向于无穷. 应用上面求解结果对第九届全国大学生数学竞赛中一题作出不一样的证明. 例1设f(x)=1-x2+x3,x∈[0,1].计算下列极限并说明理由, 解易知 0≤f(x)≤1,f在[0,1]上只有两个最大值点 ln(x+2)-ln2<ε,x∈[0,δ], 由上述引理知 (1) (2) 故 (3) 由积分中值定理,存在ξn∈[0,δ]使得 现设 由(1),(2),(3)得 命题1设f(x)在[0,1]上连续且严格单调递减,0≤f(x)≤1,f(0)=1,f′(0)=0,f″(0)≠0,则 证因为f在x=0 处取得最大值且f严格单调递减,所以 f′(x)<0,f″(0)≤0 (x>0), 由条件得f″(0)<0. 在x=0 处对f泰勒展开 令 所以 从而 同理可得 所以 由α,β的任意性,所以 设 而 最后对一般的情况即函数f在唯一最大值点处存在k阶导数(k∈+)的条件给出如下推广. 命题3设f(x)在[0,1]上连续且严格单调递减,0≤f(x)≤1,f(0)=1,f′(0)=…=f(k-1)(0)=0,f(k)(0)≠0(k∈+),则 结合命题1和命题2可以推导出有趣的斯特林公式. 证为推导斯特林公式,考虑函数f(x)=xe1-x,x∈[0,+∞).易知f在[0,1)上单调递增,在[1,+∞)上单调递减,f在[0,+∞)上有唯一最大值点f(1)=1,f′(1)=0,f″(1)=-1.一方面 应用命题1和2得 所以 另一方面经计算 所以 即 这正是斯特林公式. 即 致谢本文在很大程度上受到参考文献[1]和参考文献[2]的启发,作者非常感谢相关参考文献对本文的启发以及审稿专家提出的宝贵意见.
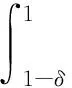


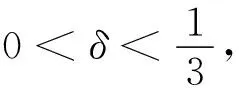



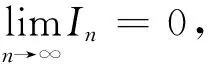
2 推 广
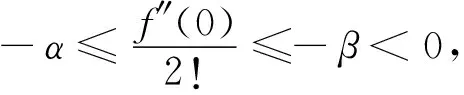
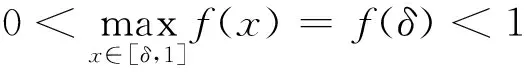
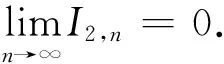


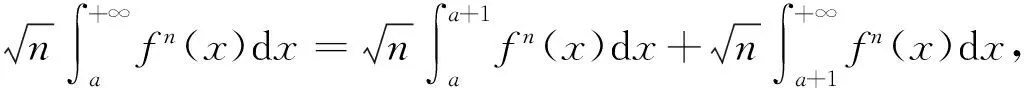
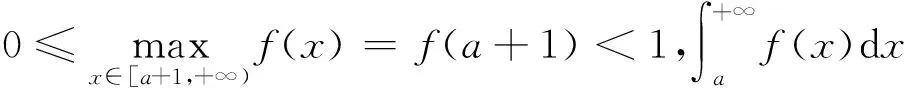
3 应 用



4 结 论

