不同回采速率下深埋矿柱的动态稳定性分析
2022-05-07韩华烨周志伟
韩华烨,周志伟,严 鹏
(1. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2. 武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072; 3. 鞍山五矿陈台沟矿业有限公司,辽宁 鞍山 114051)
深埋矿山最常使用的回采方法是房柱法或房柱嗣后充填采矿的方法[1],开采时,通过预留矿柱支撑顶部岩体以保证采场结构的稳定。然而,随着浅层矿山资源的枯竭,采矿已经逐渐向深部发展[2],进而暴露出动力破坏乃至强冲击地压等新问题[3],采场结构稳定性更加难以保证。合理的回采方式选择已经成为深埋矿山开采的焦点问题,开展相关研究将具有重要的理论意义和工程价值。
国内外学者针对矿柱稳定性分析进行了大量的研究工作。如张绍周等[4]基于压力拱理论建立了矿柱-顶板破坏模型,分析了大红山铁矿空区矿柱的稳定性,并优化了采场结构参数;王昱凯[5]等利用FLAC3D数值分析软件,通过岩石稳定性评价和类比法分析,提出了对矿柱底部巷道的稳定性对策措施;庞奇志等[6]根据矿柱回收开采期间的安全监测反馈结果,指导了后续充填工作,有效控制了采场内的地压。然而,这些工作都是基于静态计算展开研究的,忽视了矿体回采矿柱形成这一过程的动态开挖效应。Li等曾在文献[7]指出,采场预留矿柱的稳定性分析不能忽视爆破扰动和卸荷扰动等动态扰动影响,在高地应力条件下,这种作用更强,将严重影响采场的结构的稳定[7]。目前,关于矿柱受动态扰动的研究较少且不够深入,矿体回采速率(也即矿柱形成时间)这一因素的影响也经常不被考虑,基于此,本文开展了相关的研究工作。
本文将依托陈台沟铁矿地下开采工程,基于三维有限差分计算平台FLAC3D,建立矿体回采过程的数值计算模型,重点研究了不同回采速率对矿柱结构动态响应的影响,可为同类工程提供简要的参考。
1 工程概况
陈台沟铁矿埋深均在-650 m以下,最大埋深达到1 900 m,属深井开采矿山。矿床共有5条矿体,设计矿体以Fe1为主,为减少早期投资、缩短基建时间,最大化矿山效益,计划采用分期开挖方案,一期开采-1 020 m以上矿体根据其可行性研报告推荐,矿山主要采用大直径的深孔空场嗣后充填采矿的方法开采,在高地应力环境下结构稳定性及安全性管理困难。主要矿块采用盘区布置,盘区沿矿体走向布置,长度140 m,矿房平面尺寸为20 m×80 m,矿体厚度在50~80 m之间[8]。
综上,陈台沟矿体埋藏较深、地应力水平较高,深部高地应力条件下开挖诱发的松弛变形、地应力卸荷破坏(岩爆)等都将使采场矿房矿柱结构稳定性及安全管理等方面面临巨大挑战。
2 数值计算方法
2.1 有限元计算模型的建立
根据陈台沟采矿方法方案,参照矿山单盘区布置方法建立矿体回采的三维有限元计算模型,拟定矿房矿柱尺寸为20 m×80 m×50 m(宽×高×厚),为了减弱单元与边界的反射效应,数值计算模型在矿房矿柱模型四周扩大,左、右、上、下各延伸50 m,并于矿柱中心及顶部位置设置了监测点,用于监测动态开挖过程中矿柱关键部位的应力变化情况,如图1所示。单元总数576 000个,节点数594 711个。
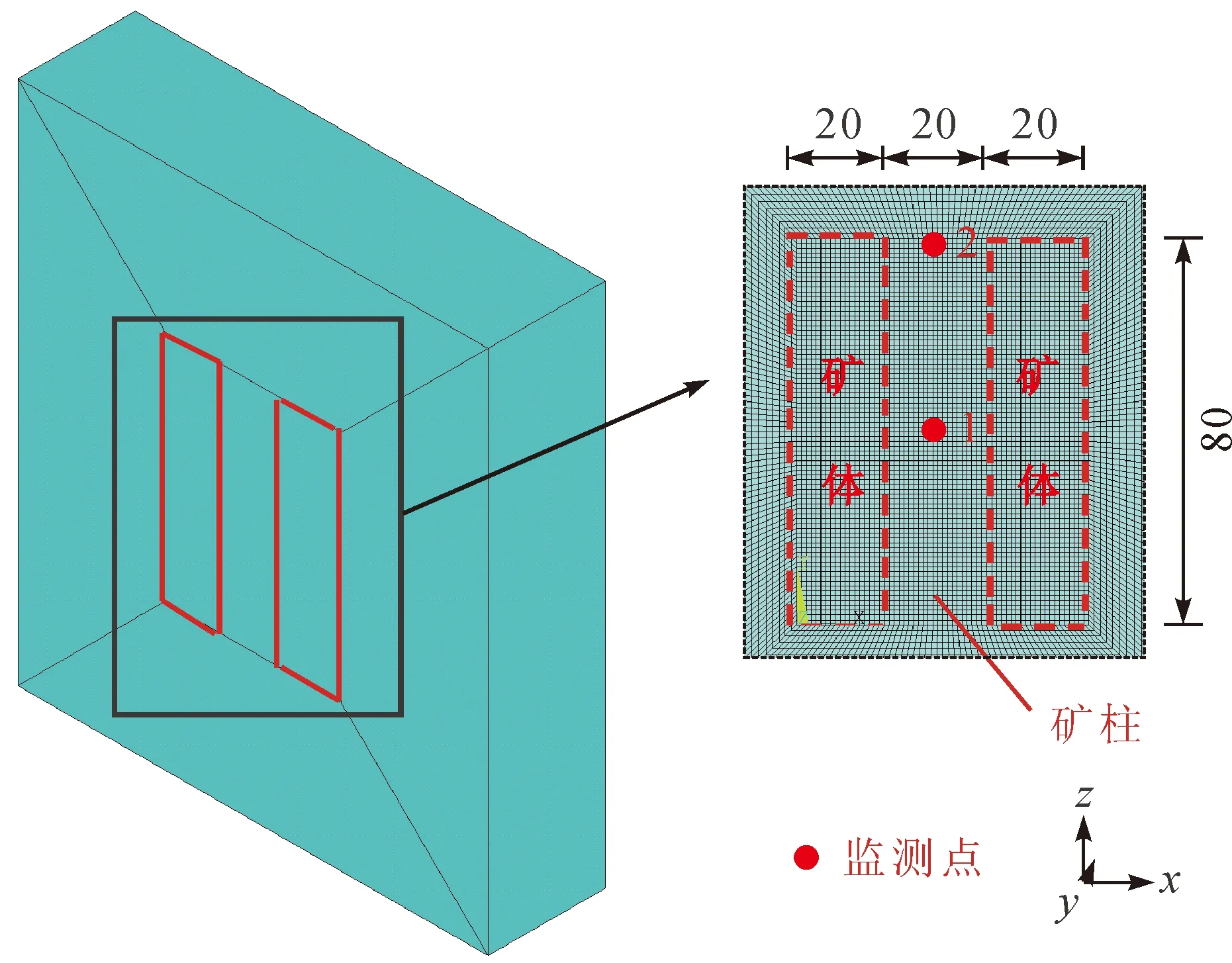
图1 有限元计算模型
为模拟真实赋存环境,模型底部采用全约束,侧面采用法向约束。应力边界采用真实的三维应力场,模型顶部施加21 MPa的地应力,水平向最大主应力25.2 MPa与轴线平行,最小主应力为22.32 MPa。由于矿柱的破坏形式以剪切破坏为主,故数值模拟中常采用Mohr-Coulomb屈服准则来模拟岩体的屈服特性[5]。开采盘区采用铁矿石来模拟,经实验室测试,其材料参数的取值可见表1。

表1 数值模拟材料参数取值
2.2 控制应力释放法
矿体崩落回采矿柱形成这一动态过程实质也是挖出矿体不再支撑顶板围岩的卸荷过程,模拟这一过程借助一种特别的模拟方法:控制应力释放法,就是求得开挖前开挖边界处开挖体对围岩的支撑力(开挖掉开挖体单元后,相应的支撑力随即消失)重建这一支撑力,然后控制其按照不同的卸荷时间进行释放,从而达到分析的目的,这一方法在许多工程的模拟中得到应用,并取得较好成效[9]。
利用FISH语言编制了应力释放程序,首先在静力计算模式下赋予模型初始地应力场,计算平衡后位移速度清零,之后模拟矿体开挖只计算第一步,提取开挖边界节点ID号及不平衡力(三向节点力),在动力模块下将其按照如图2所示的卸载路径施加在矿房边界节点并进行动力计算,同时监测矿柱关键点应力变化等反映矿柱动态响应的参量变化。
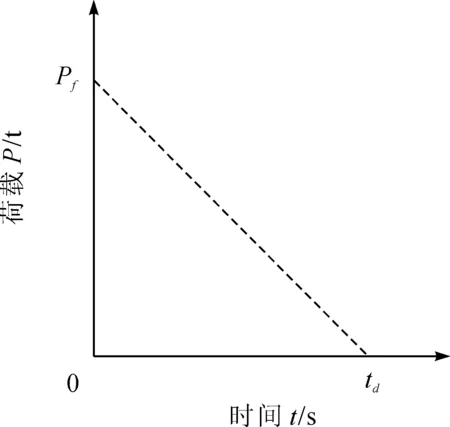
图2 支撑力卸载路径
3 数值计算结果
为了研究不同回采速率下矿柱的动态响应,计算了矿体崩落出矿历时td分别为10、20 ms和50 ms的情况,并归纳总结其各自对应的监测点应力变化、矿柱最终变形以及塑性区破坏分布情况。
3.1 矿柱监测点应力变化
图3和图4给出了不同回采速率下矿柱体关键部位的应力变化情况。在矿体回采矿柱形成后,受开挖卸荷作用的影响,矿柱体内部产生了变化的应力场,不管是最大主应力还是最小主应力,都存在一个瞬态急剧变化,之后逐渐稳定到平衡值。

图3 矿柱最大主应力变化
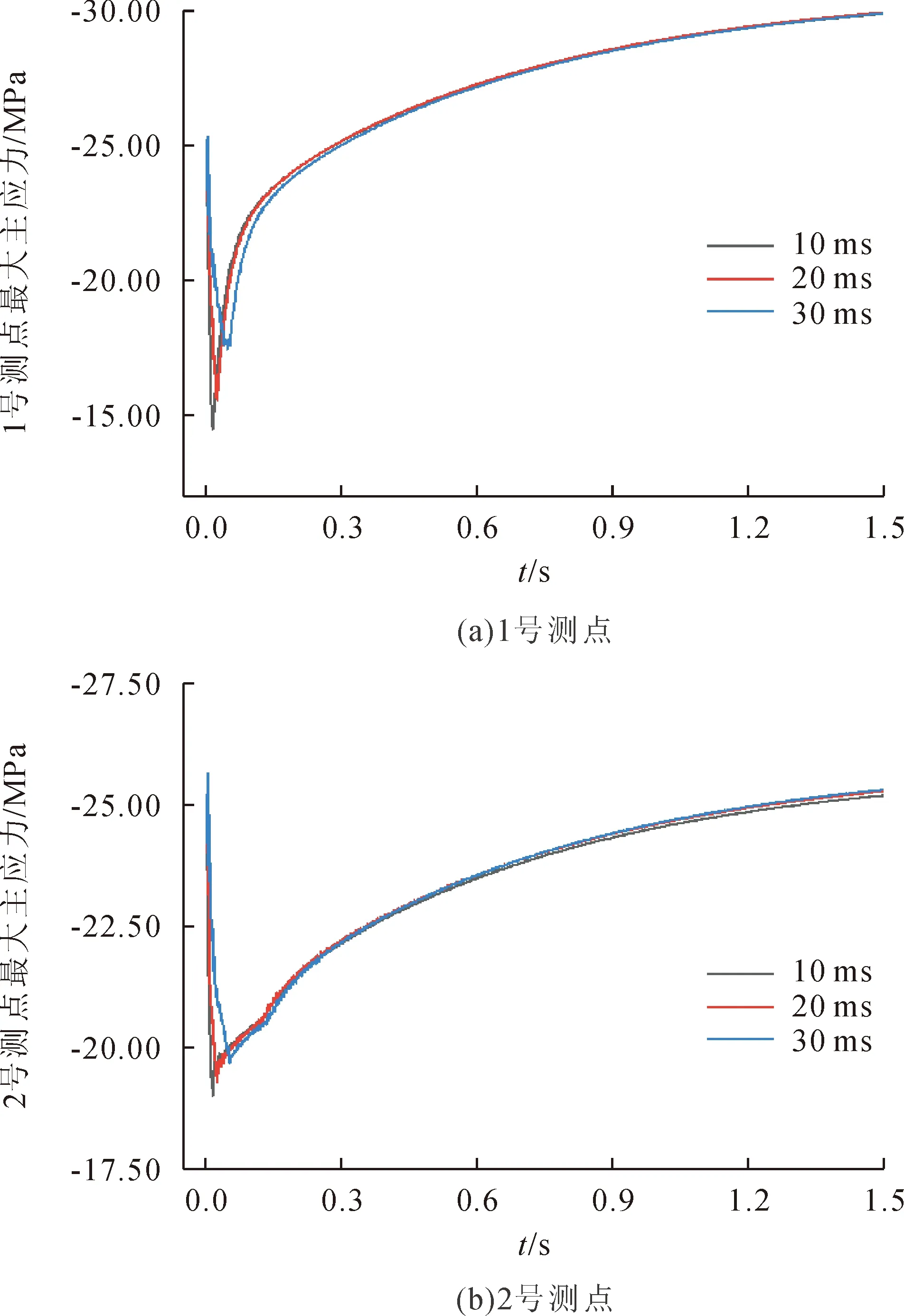
图4 矿柱最小主应力变化
进一步由图3(a)可知,对于矿柱核部位置,矿体的回采还会引起矿柱内部产生拉应力,其大小随着回采所需时间的增大而减小,10 ms时对应的最大拉应力为2.34 MPa,20 ms时对应的最大拉应力为0.98 MPa,50 ms时对应的最大拉应力为0.76 MPa。由图3(b)可知,对于矿柱顶部,矿体的回采还会引起矿柱顶部应力值的激荡变化,应力大小变化幅度随着崩落出矿所需时间的增大而减小,采用10、20 ms以及50 ms的回采时间下,矿柱顶部最大主应力大小的变化情况分别对应为6.54、5.37、3.05 MPa。
图4反映了矿体回采矿柱形成过程中矿柱关键部位的最小主应力变化情况。不难发现,相较于矿柱顶部位置,矿柱核部最小主应力变化幅度更大,采用10、20 ms以及50 ms的回采时间下,其最小主应力的变化大小分别为12.40、10.97 MPa和9.86 MPa。对于矿柱顶部,10、20 ms以及50 ms对应的最小主应力的变化大小分别为6.07、5.84 MPa和5.33 MPa。
3.2 矿柱变形情况
图5和图6给出了不同回采速率下矿柱体的水平和竖直变形情况。由图5可知,在矿体回采矿柱形成后,矿柱体产生了一定程度的水平变形,最大水平变形发生在矿柱两侧边墙的中心位置。随着回采时间的变化,矿柱最大水平变形量没有明显的变化,10、20 ms以及50 ms对应的最大水平变形大小分别为8.93、8.85 mm和8.56 mm。

图5 矿柱水平变形
图6反映了矿体回采矿柱形成后,矿柱体的竖向变形情况。可知,矿柱体产生了自下而上逐渐增大的竖向变形,底部变形最小,顶部变形最大。三种崩落出矿所需时间对应的矿柱最大竖向变形没有明显差异,其对应的最大水平变形大小分别为38.77、38.73 mm和38.56 mm。
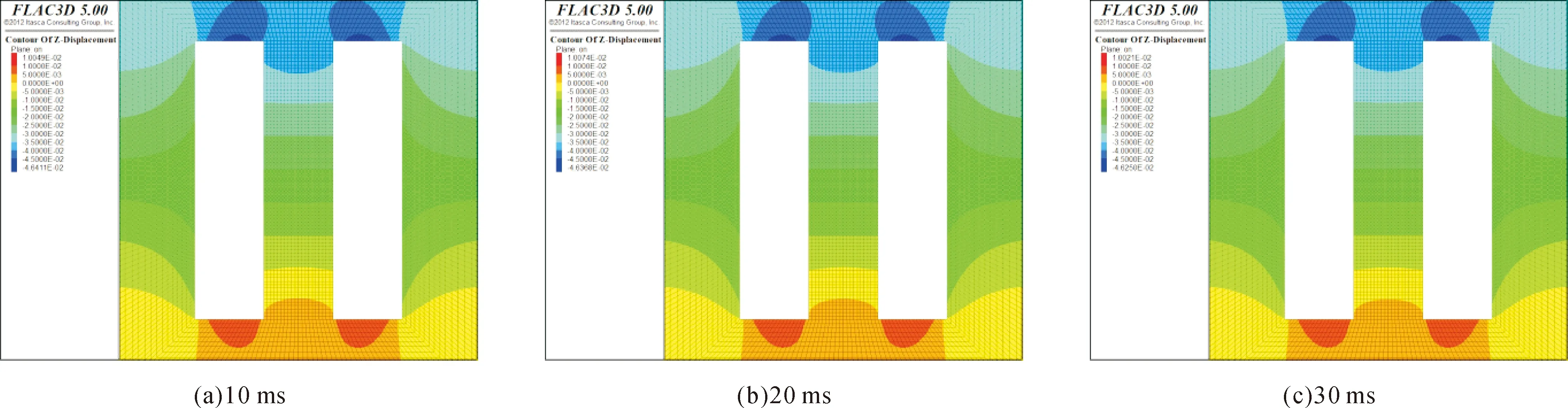
图6 矿柱竖向变形
3.3 塑性区破坏分布
矿体回采矿柱形成的过程中,由于受到二次动态应力场变化的强烈作用,不可避免地会在矿柱体内部出现一定程度的塑性破坏区域。由图7可知,随着崩落出矿时间的增大,矿柱内部产生的塑性破坏区范围越来越小,10、20 ms以及50 ms对应的矿柱塑性区面积大小分别为1 344、704、192 m2。
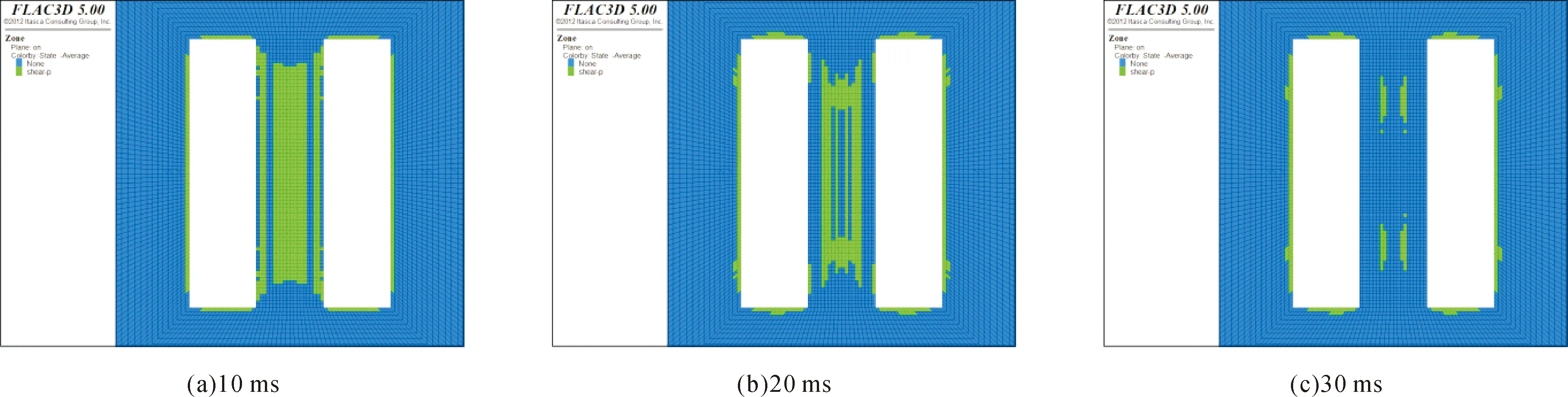
图7 塑性区破坏分布对比
3.4 不同回采时间下的动力扰动作用影响
统计采用不同回采速率下的矿柱动态响应特征值如表2所示。

表2 计算结果统计
由表2可知,当回采速率越快(也即崩落出矿所需时间的越小),矿柱中主应力变化幅度,矿柱最终水平、竖直变形量以及因应力动态调整作用所形成的的塑性破坏范围均越大,说明相同的尺寸参数设计的情况下,控制回采速率对于保护矿柱的稳定性具有重要意义,在生产中应在考虑炸药参数、生产方式的基础上尽可能延长矿体回采所需时间。当采用50 ms开挖时,动态响应程度已经较小,矿柱稳定性情况较好,在生产中可予以采用。
4 结 语
本文依托于陈台沟地下采矿工程,针对深埋矿山矿柱体的结构稳定安全这一问题,采用数值模拟的方法,研究分析了不同回采速率下矿柱体的动态响应,结论总结如下。
1)随着矿体崩落矿柱形成所需时间的增大,矿柱体受瞬态开挖作用而产生的动态响应程度有所减小,具体可表现为动态主应力变化幅度、矿柱最大水平、竖向变形量以及塑性破坏区域的减小。在生产实际中,应尽可能延长矿体崩落出矿所需时间。
2)根据数值模拟对10、20 ms以及50 ms三种不同崩落时间下的陈台沟地下采场矿柱稳定性的分析可知,50 ms情况对应的矿柱稳定性最好,建议在生产中可予以采用。
