非常规油气藏压裂水平井动态缝网模拟方法及应用

2022-05-07刘传喜方文超秦学杰

石油与天然气地质 2022年3期

刘传喜，方文超，秦学杰

（中国石化石油勘探开发研究院，北京 100083）

非常规油气藏压裂水平井进入生产期，压裂缝网形态并不是静态不变的，而是随着开发过程的进行，缝内压力发生变化，表现出动态缝网特征［1-4］。2016年，Vermilye等［5］采用生产期微地震监测手段，获取一口压裂水平井投产后由于应力和流体扰动所产生的微地震事件点，证实了缝网的动态变化特征，并提出了动态生产体积APV（active production volume）概念。监测结果表明储层中的压裂改造范围在生产期迅速缩小，2年后的APV约为初始改造体积的一半，3年后的APV几乎消失。这与目前非常规油气藏生产井初期产量相对较高但随后快速递减并维持长期低产的生产规律相吻合［6-7］。

压裂缝网的动态变化对生产期储层的供给能力和井的产量大小具有重要影响，是开发调整方案制定和实施的重要依据［8-10］。但目前尚未建立针对实际储层中缝网动态变化过程的数值模拟方法，即目前用于油藏数值模拟的缝网模型保持为压裂后的初始缝网形态，不随储层压力发生变化。本研究在构建压裂缝网形变数学模型和数值模型的基础上，采用传导率修正技术将裂缝形变模型与离散裂缝数值模拟器进行耦合，研发了具有模拟动态缝网功能的数值模拟器，并开展实例应用。

1 裂缝形变数学模型

非常规油气藏水平井压裂形成缝网后，随着开采进行，裂缝中流体压力会产生较大波动，加之裂缝面上岩石应力的作用，导致开采过程中裂缝属性（宽度和渗透率）发生变化。实验表明［11-13］，压裂裂缝宽度随裂缝面上有效应力的变化遵循双曲模型（图1）。曲线的变化分为3个阶段：随着裂缝面上有效应力的增大（缝内压力降低），初始阶段裂缝宽度呈非线性急剧下降；裂缝空间压缩到一定程度后，支撑剂的抗压强度发挥作用，此时继续增大有效应力则使裂缝宽度呈缓慢拟线性下降；当裂缝空间压缩逼近极限时，裂缝宽度对有效应力变化不敏感，此时宽度变化进入平缓段。3个阶段在横坐标上的分界点为σ1（有效应力，MPa）和σ2，其中σ2为裂缝宽度下降至极限点的极限有效应力，MPa；对应的宽度称为残余裂缝宽度wr，m；当有效应力大于σ2后，所建立的数学模型规定裂缝宽度不随有效应力的变化而变化，保持为wr。

将图1的双曲模型用如下公式进行定量表征：

式中：wf为裂缝宽度，m；wmax为初始裂缝宽度，m；β为与裂缝力学性能相关的无因次特征参数；Ψ为裂缝刚度，MPa；σn为裂缝面上有效应力，MPa，其计算公式为：

式中：σnormal为裂缝面上的总正应力，MPa；pf为裂缝内的流体压力，MPa。

特征参数β的计算表达式为：

式中：θres为无因次残余裂缝宽度系数，即残余裂缝宽度与最大裂缝宽度的比值：

裂缝刚度Ψ与双曲模型曲线的曲率密切相关，Ψ越大，曲率越小，意味着裂缝宽度下降的速度越小，曲线越接近线性，如图2所示，图中计算参数分别为σ2=20 MPa，θres=0.1。

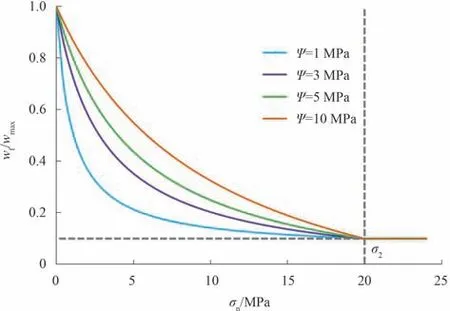
图2 裂缝变形双曲模型曲线形态与裂缝刚度之间的关系Fig.2 Hyperbolic curves for fracture deformation under different fracture stiffness

在实际储层中，沿裂缝走向的裂缝宽度分布并不是一个定值，而是呈“两头窄中间宽”的分布形态。为实现对裂缝变形更加真实的模拟，先对裂缝进行线剖分，然后采用二次函数对各个线单元的初始裂缝宽度wmax进行赋值（图3）。

图3 实际裂缝宽度的非均匀分布及其表征方法Fig.3 Non-uniformdistribution of fracture width along a real fracture and the characterization method of the fracture width distribution

将描述裂缝宽度随应力变化的双曲模型与描述裂缝宽度非均匀分布的二次函数模型进行结合，则不仅可模拟生产过程中裂缝宽度的变化，还可以模拟裂缝长度的变化，使裂缝变形模拟更贴近实际（图4）。

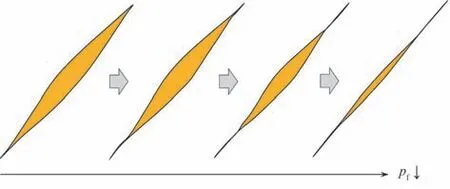
图4 模拟裂缝长度和宽度动态变化示意图Fig.4 Schematic sketch of the dynamic fracture width and length modeled in the simulator

2 裂缝形变数值模拟方法

采用基于非结构化网格的离散裂缝模型（DFM）开展裂缝形变模拟，离散裂缝模型在模拟过程中保持了裂缝原始分布和形态，对裂缝形变过程的模拟具有较好适应性。技术思路为：通过传导率修正的方式，将裂缝形变数学模型与离散裂缝数值模拟模型进行耦合，形成具有模拟裂缝形变功能的离散裂缝数值模拟器。

2.1 离散裂缝模型传导率计算

在DFM模型中，任意两个相邻网格i和j之间的传导率可采用以下公式计算［14］：

式中：Tij为i和j之间的全传导率，m3；Ti和Tj分别为网格i和网格j与网格交界面之间的半传导率，m3。

上式即为DFM模型中常采用的两点流动近似（TPFA）方法［15-16］。该方法分开计算不同类型介质（基质、裂缝）的传导率，更易于观察不同类型介质中流动机理的不同。

单个网格与网格交界面之间半传导率的计算公式为：

式中：Aij为网格i与j的网格交界面面积，m2；Ki为网格i渗透率，m2；d为网格交界面到网格中心点（基质网格为三角形形心，裂缝网格为四边形对角线交点0）垂直距离，m。对于裂缝网格：

如图5所示，DFM模型的网格类型有两种，分别为基质网格（m）和裂缝网格（f），对应着两种网格半传导率Tm和Tf。网格的邻接类型有3种，分别为基质-基质（①）、基质-裂缝（②）和裂缝-裂缝（③），对应着3种全传导率Tm-m，Tm-f和Tf-f。对裂缝形变进行模拟的核心方法就是利用裂缝形变数学模型对裂缝半传导率进行修正，进而修正与裂缝网格相关的全传导率，达到裂缝形变与流体流动耦合模拟的目的。

图5 模拟器中2种网格和3种传导率示意图Fig.5 Schematic sketch of two kinds of grids and three kinds of transmissibility in the simulator

2.2 裂缝形变数值表征

将裂缝形变模型与裂缝网格半传导率耦合，即将公式（1）代入公式（6）：

式中：Tf0为裂缝网格初始半传导率，m3，计算式为：

式中：Ai，f表示网格i与裂缝网格f交界面面积，m2；Kf为裂缝网格渗透率，m2。考虑裂缝形变效应的裂缝半传导率具有时变特征，公式（8）中σn与裂缝中的流体压力密切相关。考虑裂缝变形效应的跨尺度耦合流动全传导率计算仍基于TPFA方法［公式（5）］，此时，与裂缝网格相关的全传导率（基质-裂缝，裂缝-裂缝）也具备时变特征。即，基质网格（m）-裂缝网格（f）流动全传导率计算公式为：

裂缝网格（f1）-裂缝网格（f2）流动全传导率计算公式为：

在模拟计算过程中，首先计算出只与网格几何参数有关的裂缝网格初始半传导率矩阵，而后在每一步模拟过程中对半传导率和全传导率进行修正。

3 动态缝网模拟实例应用

3.1 典型模型动态缝网模拟

建立致密油藏中一口多段压裂水平井典型模型，如图6所示，以直观研究裂缝形变效应对油藏开发的影响。典型模型的尺寸为400 m×200 m，水平井长度设计为300 m，压裂段数为7段，半缝长为60 m。

图6 用于裂缝形变效应模拟的多段压裂水平井网格模型Fig.6 Mesh model containing multi-stage fractures for the simulation of fracture deformation

表1总结了涉及到的模拟参数，模拟时间为365 d。裂缝应力参数设置为：残余裂缝宽度系数θres=0.1，极限有效应力σ2=12 MPa，油藏总正应力在各网格间均匀分布σnormal=20 MPa。为模拟水力压裂缝的缝宽在长度方向上的非均匀分布现象，对每一条裂缝的不同位置赋了不同的缝宽初值，每条裂缝的宽度呈现“两头窄中间宽”的分布规律，缝宽范围为1～10 mm。

表1 多段压裂水平井模型数值模拟参数Table 1 Simulation parameters of the multi-stage fractured well model

模型中设置的裂缝形变程度分为无裂缝形变、弱裂缝形变（Ψ=10 MPa）、强裂缝形变（Ψ=2 MPa）。利用模拟器计算得到的水平井产量和累计产量变化曲线如图7所示。由图可知，裂缝形变显著降低了油井初产，其后一直保持低产水平，主要因为在衰竭式开采条件下，开井初期裂缝中的压力快速下降，导致裂缝快速闭合，储层供给能力急剧降低，从而极大降低了水平井产能，如图8所示不同裂缝刚度对应的不同模拟时间点压力分布图。图8表明，考虑裂缝形变效应后，裂缝的导流能力显著降低，井周围的压降幅度明显缩小。此外，对比可看出，Ψ=2 MPa时，裂缝导流能力的减弱首先发生在裂缝的两端，且减弱程度最大。当裂缝中间处的导流能力处于相对较高的水平时，裂缝两端的压降程度仍然很小，这主要是因为裂缝两端的宽度小，因此在压力下降过程中优先闭合。

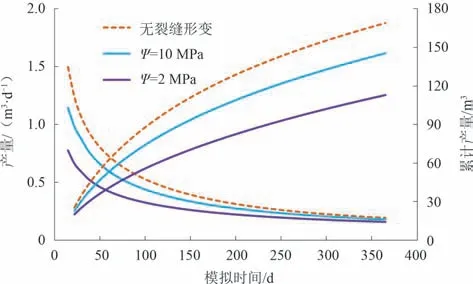
图7 不同裂缝刚度对应的水平井生产动态曲线Fig.7 Production dynamic curves obtained under different fracture stiffness

图8 不同裂缝刚度对应的压力分布变化Fig.8 Reservoir pressure variation under different fracture stiffness with time

图9为不同时期缝网裂缝宽度分布图，即动态缝网模型。可看出，裂缝形变的过程由裂缝两端向中间延伸。在生产初期，裂缝形态变化较剧烈，闭合速度较快；到了生产中后期，闭合速度变慢；模拟期末，裂缝两端的缝宽基本接近极限宽度，这与图1所示的裂缝宽度的双曲变化规律相吻合。

图9 数值模拟不同生产时期的动态缝网模型Fig.9 Dynamic fracture network models at different production periods in the numerical simulator

3.2 实际井动态缝网模拟

为研究油田实际井的动态缝网变化特征及其对井产量的影响，选取鄂尔多斯盆地某致密油藏EN125井开展动态缝网构建和油藏数值模拟。EN125井水平段长780 m，压裂段数7段，泵注总液量1 482 m3，总砂（陶粒）量176 m3，排量3 m3∕min，井周围局部发育有天然裂缝。采用压裂模拟方法预测了该井的压裂缝网模型，如图10a所示。

图10b为EN125井离散裂缝数值模拟网格模型，基质渗透率0.36×10-3μm2，基质孔隙度8%，裂缝初始宽度范围1～10 mm，原始油藏压力18 MPa，流体粘度3.2 mPa·s，模型考虑了致密油藏启动压力梯度，实验测试结果为0.18 MPa∕m。拟合后的压裂裂缝形变参数：残余裂缝宽度系数θres=0.1，裂缝刚度Ψ=2 MPa，极限有效应力σ2=12 MPa，油藏总正应力在各网格间均匀分布σn=18 MPa。

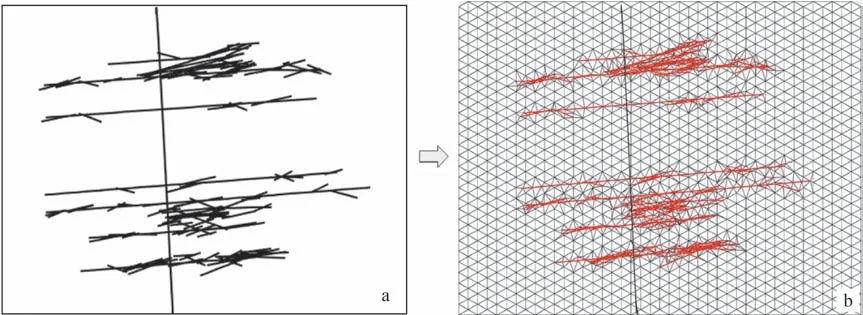
图10 EN125井压裂缝网模型（a）及对应的油藏数值模拟网格模型（b）Fig.10 Fracture network model（a）and corresponding reservoir numerical simulation mesh model（b）for Well EN125

图11为模拟1年得到的EN125井在不同时期的动态缝网模型。可见，裂缝动态闭合主要发生在生产初期的1～2个月内，到后期逐渐放缓。整个过程中动态缝网的变化规律为：主裂缝沟通的天然裂缝首先闭合，水力裂缝的宽度变小；而后水力裂缝由两端向中间逐渐闭合。图11表明，压裂形成的初始缝网在1年后会发生显著变化，缝网规模明显变小，与文献中的实际井监测结果相符［5］。

图11 EN125井不同生产时期的动态缝网模型Fig.11 Dynamic fracture network models at different production periods for Well EN125

为更直观研究动态缝网对压裂水平井产量的影响，采用离散裂缝数值模拟器对EN125井开展了两种情况下的模拟。一种情况是考虑裂缝闭合，另一种情况是不考虑裂缝闭合，其他参数均一致。将两种情况下的模拟产液量与该井实际产液量进行拟合，结果如图12所示。

图12表明，当不考虑裂缝闭合时，模拟产液量明显高于井的实际产液量，特别是初期产量吻合率较低，因为此期间储层中裂缝闭合对产量的影响并未在模拟器中体现。而在相同物性和流体参数条件下，当在模拟器中考虑裂缝闭合时，模拟产液量与实际产液量差别较小，特别是初期产量较容易拟合上。因此，动态缝网对致密油藏压裂水平井的产量影响显著，在数值模拟过程中考虑动态缝网更加符合致密油藏生产实际，开发方案设计精度也将更高。