2021年新高考数学多选题的解题策略与命题趋势探析

安徽 张 超 王玉佩

多选题在高考数学中是一种创新题型，该题型为不同层次的考生提供了更多的得分空间，同时更加科学地发挥了高考的区分和选拔功能，为高校合理分层培养提供有效支撑，因而深受广大师生的欢迎和关注.安徽省即将使用数学新高考卷,作为一线的一名数学教师，分析、研究多选题这一新题型的结构、特点，与总结探讨多选题解题策略，非常有必要.为此，笔者结合2021年高考多选题的结构、特点及解题策略等三个方面谈一下思考和认识，与读者共同交流探讨.

一、2021年新高考数学多选题的结构与特点

1.多选题的结构

多选题是高考数学三大题型之后在新高考数学卷中出现的一种新题型，全卷试题结构按单项选择题、多项选择题、填空题和解答题排列.所谓多选题就是围绕一个主题，设计多个符合条件的正确选项供考生选择，这是多选题和单选题的主要区别.新高考中多选题设置4 个选择题，题号顺序是第9题至第12题,每个选择题设置4个选项，分别为A，B，C，D，每题满分为5 分，共 20分.得分规则是“全部选对的得5分 ，有选错的得0分，部分选对的得2分”.

2.多选题的特点

多选题具有分值小、解题思路广的特点，和传统单选题相比，多选题的设置给多数考生增加了得分机会，但是不容易得全分；考试中不免有考生因选出不正确选项而得0分；多数考生能够选对部分正确选项得2分，因此多选题有较强的区分度，提升了考试的信度和效度.

下面结合2021年新高考Ⅰ卷试题加以剖析，旨在探索题型特点、规律，揭示解题策略.

二、多选题解题策略分析

1.直接法

从题设条件出发，运用有关概念、性质、定理、法则和公式等，通过正确的运算、推理或判断，直接得出结论，从而得出正确答案的一种方法.运用此种方法解题需要扎实的数学基础.

【例1】(2021·新高考Ⅰ卷·9)有一组样本数据x1,x2,…，xn，由这组数据得到新样本数据y1,y2,…，yn，其中yi=xi+c(i=1,2，…，n)，c为非零常数，则

( )

A.两组样本数据的样本平均数相同

B.两组样本数据的样本中位数相同

C.两组样本数据的样本标准差相同

D.两组样本数据的样本极差相同

B，若第一组数据的中位数为x，则第二组的中位数为x+c，显然不相同，错误；

C，若第一组数据的方差为S2，则第二组数据的方差也是S2，故方差相同，正确；

D，由极差的定义知，若第一组的极差为xmax-xmin，则第二组的极差为ymax=(xmax+c)-(xmin+c)=xmax-xmin，故极差相同，正确，故选CD.

评注：该题是以统计知识为考查素材，只要统计概念清晰即可正确判断.

通过该题说明老师在教学中要注重引导学生对平均值、方差概念的理解.因为在新高考中，越来越重视概念的考查.这也体现新高考注重基础知识、基本技能及生活的考查理念.

2.综合法

综合法通常就是指应用直接法、特殊值法、排除法等,从而得出正确结论的方法.综合法是解答数学多选题的常用方法.

【例2】(2021·新高考Ⅰ卷·10)已知O为坐标原点，点P1(cosα,sinα)，P2(cosβ,-sinβ)，P3(cos(α+β),sin(α+β))，A(1,0)，则

( )

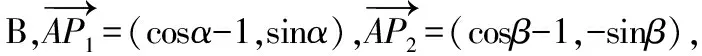
另外该题也可以采用数形结合法快速选出正确选项，通过该题需要注意解答多选题和单选题解法上有很大区别，比如解单选题时我们经常会采用所谓“投机取巧”的方法，例如,特殊值法、排除法、极端性原则等，这些方法解多选题就要慎用，多选题更加注重基本功和通性通法的考查.

3.数形结合法

数形结合是数学解题当中最常用的方法之一.运用数形结合思想，可以使抽象的数学问题变得更加生动、直观，有助于学生把握数学问题的本质，这样便使很多抽象的数学问题迎刃而解，让“难懂”的解法变得容易理解和消化.

【例3】(2021·新高考Ⅰ卷·11)已知点P在圆(x-5)2+(y-5)2=16上，点A(4,0),B(0,2)，则

( )

A.点P到直线AB的距离小于10

B.点P到直线AB的距离大于2

详解：圆(x-5)2+(y-5)2=16的圆心为M(5,5)，半径为4，

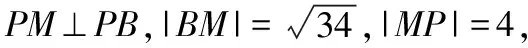
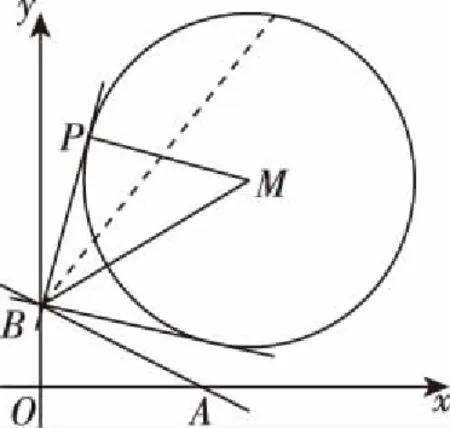
评注：本题是以直线与圆有关的最值相关知识点作为背景.由于圆既能与圆锥曲线相联系,又能与平面几何相结合,命题方式比较灵活,故与圆相关的最值问题备受命题者的青睐.在运动变化中,动点到直线、圆的距离会发生变化,在变化过程中,就会出现一些最值问题,如距离、角最小、最大等.这些问题常常联系到平面几何知识,利用数形结合思想可直接得到相关结论,解题时便可利用这些结论直接确定最值问题,故在此提醒考生解题时千万不要得“意”忘“形”.

4.保底法

对于多选题中的压轴题,难度一般较大,宜采用保底法，即当有些选项在一定时间无法确定是否正确时，可选定其他正确的一个保住基本分，因为部分选对也可得2分(这比单选题的得分概率要高)，我们把这种解题策略称为保底法.当然,如果学生整体素质较高,或者对题目十分熟悉,则另当别论．

( )

A.当λ=1时，△AB1P的周长为定值

B.当μ=1时，三棱锥P-A1BC的体积为定值

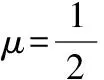
详解：易知，点P在矩形BCC1B1内部(含边界)．

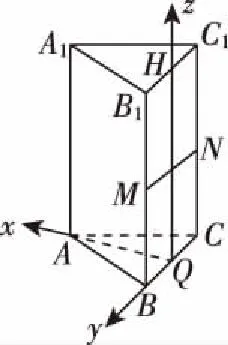
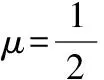
评注：本题是以立体几何知识为素材，属于选择题中的压轴题.多选题中的立体几何试题，常把多个知识点交汇考查，如把几何体长度、角度、面积、体积的计算与线面位置关系结合在一起考查，也可与函数、不等式及空间向量结合在一起考查，此类问题对学生直观想象及逻辑推理的核心素养要求较高，难度也比较大.

三、多选题命题趋势和教学启示

通过2021年新高考Ⅰ卷试题分析，笔者得到如下教学启示：

1.从命题角度看，该试题是以统计、三角函数、向量、圆锥曲线(直线和圆)、立体几何综合问题等为背景进行试题设计，其主要原因是三角函数图象和性质等特点多样，命题入手点相对较宽,直线和圆试题中数形结合动态分析能够较好地体现区分度.但是从命题的着手点来看新高考相对于旧高考有了较大的变化，命题的载体向生活化、灵活化倾斜等，所以还是不能偏颇的认为只有这些载体，例如考查以初等基本函数为载体，加绝对值等手段考查函数性质等等，但是不论新高考如何变化老师在教学中还是要强调基础的稳固，适当的延伸，关注情境和生活化的试题，注重重大考试的变式演练.

2.从解题策略角度看，2021年新高考多选题分别用到了常用的直接法、综合法、数形结合法、保底法等.在解题策略上更加注重通性通法，对学生基础知识和解题技巧要求更高.

3.从数学核心素养角度看，2021年新高考试题对于数学核心素养的考查比较全面，其中数学运算、逻辑推理核心素养的考查力度很大，所以在以后新高考中对数学核心素养的考查会更加全面，这就要求一线老师在教学中注重数学核心素养的渗透.

四、结语