例谈“概率与统计”主题的学科一般观念

安徽 陈绪丰 祝 峰

高中数学中可以把概率与统计、三角、解析几何、立体几何、数列等相对独立的数学分支视为一个学科．学科一般观念是指对本学科学习和研究具有广泛、持久、深刻影响的基本数学思想方法和基本思维策略．这些数学思想和思维策略是构建学科知识，利用学科知识提出问题、分析问题、解决问题的思维方向和行为策略．它们是学好本学科的基础和关键，是解决本学科问题的金钥匙．数学教学中，需要有意识地培养学生从基本概念、基本原理及其联系出发，来思考和解决问题，持续关注学生学科一般观念的发展．学科一般观念的缺失或薄弱，会导致学科学习松散化、碎片化，问题解决游离化、机械化．特别是高考备考教学，其知识的回顾性、系统性与综合性为发展学生的学科一般观念提供了良好契机．树立并强化学科一般观念是提高学生应试能力的大道和王道，更是发展学生思维能力、培养学科核心素养的正道．下文结合实例，呈现概率与统计主题中包括概念观、原理观、符号观、分析观、模型观、图形观在内的，六种核心学科一般观念，旨在为概率与统计主题的高考复习提供一个全新的备考视角．

一、概率统计主题的内容要求

《普通高中数学课程标准(2017年版2020年修订)》的课程内容设置中，必修课程和选择性必修课程均包括概率与统计主题．

1.必修课程

必修课程中设置在主题四，包括概率、统计两个单元．

(1) 概率单元内容包括：随机事件的概率、随机事件的独立性．要求学生结合实例，理解样本点、有限样本空间、随机事件，会计算古典概型中简单随机事件的概率，加深对随机现象的认识和理解．

(2)统计单元内容包括：获取数据的基本途径及相关概念、抽样、统计图表、用样本估计总体．要求学生进一步学习数据收集和整理的方法、数据直观图表的表示方法、数据统计特征的刻画方法；通过具体实例，感悟在实际生活中进行科学决策的必要性和可能性；体会统计思想与确定思想的差异、归纳推理与演绎证明的差异；通过实际操作、计算机模拟等活动，积累数据分析的经验．

2.选择性必修课程

选择性必修课程中设置在主题三，是必修课程中概率与统计内容的延续，包括计数原理、概率、统计三个单元．

(1)计数原理单元内容包括：两个基本计数原理、排列组合、二项式定理．本单元可以帮助学生理解两个基本计数原理，运用计数原理探索排列、组合、二项式定理等问题．

(2)概率单元内容包括：随机事件的条件概率、离散型随机变量及其分布列、正态分布．本单元的学习，可以帮助学生了解条件概率及其与独立性的关系，能进行简单计算；感悟离散型随机变量及其分布列的含义，知道通过随机变量更好地刻画随机现象；理解伯努利试验，掌握二项分布，了解超几何分布；感悟服从正态分布的随机变量，知道连续型随机变量；基于随机变量及其分布解决简单的实际问题．

(3)统计单元内容包括：成对数据的统计相关性、一元线性回归模型、2×2 列联表．本单元的学习，可以帮助学生了解样本相关系数的统计含义，了解一元线性回归模型和2×2列联表，运用这些方法解决简单的实际问题．会利用统计软件进行数据分析．

二、概率统计主题的学科一般观念1.概念观

概念是进行逻辑判断的基本依据，是数学思维的最小单元．“核心概念往往具有鲜明的直观背景，简单、易懂且威力无穷．”概率统计主题的复习备考中，应引导学生回到概念思考问题的习惯，远离“题型+技巧”的雕虫小技，集中注意力于核心概念，学会用概念分析和解决问题，只有这样才能实现“减轻负担，提高质量”的高效备考．

【例1】(2021·新高考Ⅰ卷·8)有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球.甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则

( )

A.甲与丙相互独立

B.甲与丁相互独立

C.乙与丙相互独立

D.丙与丁相互独立

答案：B

依据相互独立事件的概念知，只有甲与丁两事件相互独立，故选B.

评析：本题回归到古典概型、排列组合、相互独立事件的定义上.依据古典概型的定义，分别求出相关事件的概率；再由两个随机事件相互独立的含义，如判断事件之间的独立性.判断事件A，B是否独立，只需先计算对应概率，再判断P(A)·P(B)=P(AB)是否成立.

2.原理观

概率研究的对象是随机现象，主要是从不确定性角度认识客观世界，并提供随机现象研究特有的思维模式和问题解决方法； 概率为统计的学习提供理论基础.概率与统计问题的统计思想有别于确定性思维，所用到的归纳推断也有别于演绎证明.要求学生在学习过程中，要整体遵循不确定、随机、归纳等一些基本的原理.

【例2】(2021·新高考Ⅰ卷·9)有一组样本数据x1，x2，…,xn，由这组数据得到新样本数据y1，y2，…，yn，其中yi=xi+c(i=1,2,…,n),c为非零常数，则

( )

A.两组样本数据的样本平均数相同

B.两组样本数据样本中位数相同

C.两组样本数据的样本标准差相同

D.两组样本数据的样本极差相同

答案：CD

解析：对于A，E(y)=E(x+c)=E(x)+c且c≠0，故平均数不相同，错误；对于B，若第一组中位数为xi，则第二组的中位数为yi=xi+c，显然不相同，错误；对于C，D(y)=D(x)+D(c)=D(x)，故方差相同，正确；对于D，由极差的定义知，若第一组的极差为xmax-xmin，则第二组的极差为ymax-ymin=(xmax+c)-(xmin+c)=xmax-xmin，故极差相同，正确，故选CD.

评析：聚焦样本数据的平均数、中位数、标准差、极差的概念及实际意义，考查样本数据线性复合后，其相关数字特征之间关系的基本原理.一组样本数据x1，x2，…，xn，由这组数据得到新样本数据y1，y2，…，yn，其中yi=kxi+c(i=1,2,…,n),c为非零常数，则两组数据的数字特征之间存在着关系，可依据概念予以推导.

3.符号观

高中阶段概率与统计专题的学习中，符号意识同样关键，要求学生能够理解并运用规范的符号表示事件、事件关系，以及常见的统计数据和统计模型.能够自觉地使用符号描述随机现象和统计规律，并借助符号进行归纳、推理和运算.

在概率与统计主题的高考备考中，树立符号观念，有助于学生理解概念、原理的本质.养成善于使用符号进行数学表达和数学思考的习惯，善于将冗长、烦琐的文字描述转换符号表达，使概率统计问题的思考、解决、表达和交流简单、直接、明了.

4.分析观

包含“发现、提出、分析、解决问题”在内的“四能”课程目标中，发现和提出问题的能力在学习过程中意义突出，但应试过程中“分析问题”的能力却尤为重要.应试中问题是现成的，并不需要发现和提出问题，合理、深入、全面的分析问题是顺利解决问题的前提和保障.概率与统计主题高考备考中，分析问题有其特殊内容指向和手段，主要包括实际问题的模型化分析、随机事件构成和关系的分析、样本数字的特征分析、用样本的数字特征估计整体的合理性分析等.高三备考的概率与统计主题教学中，应通过实例，训练学生从概念原理的分析视角，丰富多措并举的分析手段，强化确定范畴、厘清关系的分析标准，树立分析在前、解决在后的问题分析观.

【例4】(2021·新高考Ⅰ卷·18)某学校组织“一带一路”知识竞赛，有A，B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束.A类问题中的每个问题回答正确得20分，否则得0分；B类问题中的每个问题回答正确得80分，否则得0分.已知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关.

(1)若小明先回答A类问题，记X为小明的累计得分，求X的分布列；

(2)为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由.

答案：B类

解析：(1)小明先回答A类问题，其答题情况共三类：①A类问题答错，得0分，比赛结束；②A类问题答对，且B类问题答错，得20分，比赛结束；③A类问题答对，且B类问题答对，得100分，比赛结束.上述三种情况对应事件互斥，同时注意到两类问题能否正确回答相互独立.所以X的取值可能为0，20，100.

P(X=0)=1-0.8=0.2；

P(X=20)=0.8×(1-0.6)=0.32；

P(X=100)=0.8×0.6=0.48.

所以X的分布列为

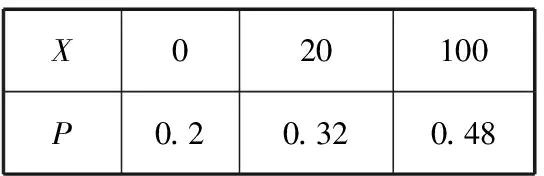
X020100P0.20.320.48

(2)由(1)知，E(X)=0×0.2+20×0.32+100×0.48=54.4.若小明先回答B问题，记Y为小明的累计得分，则Y的所有可能取值为0，80，100.

P(Y=0)=1-0.6=0.4；

P(Y=80)=0.6×(1-0.8)=0.12；

P(Y=100)=0.8×0.6=0.48,

所以E(Y)=0×0.4+80×0.12+100×0.48=57.6.

E(Y)>E(X)，所以小明应选择先回答B类问题.

评析：分析小明答题的所有情况，明确各情况的关系，是清晰准确运算出各情况所对应事件概率的前提和基础.如第(1)问中，且B类问题答错是答对的对立事件，A类问题答对和B类问题答错是相互独立事件，所以P(X=20)=0.8×(1-0.6)=0.32，复杂事件的概率求解中，应先分析事件的构成情况，明确其由哪些子事件的构成，这些子事件的关系是怎样的，才能准确求得随机事件的概率.

5.模型观

在必修及选择性必修课程的概率与统计主题学习中，有大量常见特殊的问题情境.如排列组合中的相邻问题、不相邻问题、局部顺序确定问题、分组分堆问题、至少问题；概率中的古典概型、几何概型、条件概率；统计中的线性回归分析、超几何分布、二项分布、正态分布等，可以把这些典型的问题视为特殊模型.问题解决过程中，应树立模型观念，在模型观念的引领下，仔细分析问题情境，排除干扰因素，抓住关键，厘清本质，将具体问题归结到确定的模型上，问题即可快速得到准确的解答.

【例5】(2021·全国乙卷理·6)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有

( )

A.60种

B.120种

C.240种

D.480种

答案：C

评析：排列组合问题中“分组、分堆问题”“至少”问题.“至少”问题模型中，应先分组，即把5人分成2,1,1,1四组，再排列.

6.图形观

图形观是指借助图形和想象，运用概率与统计的方法来感知随机现象，利用几何直观理解和解决概率和统计问题的思维习惯.主要包括：借助几何直观认知随机事件的关系、构成及规律；利用图表及图形来描述、分析概率与统计问题；建立随机现象与几何直观的联系，构建概率与统计问题的直观模型、探索问题解决的思路.

( )

答案：B

解析：如图，设从区间(0,1)，(1,2)中随机取出的数分别为x、y，则实验的所有结果构成区域为Ω={(x,y)|0

评析：借助线性规划知识，利用平面区域描述问题情境中的随机现象.首先用不等式组描述随机现象的样本空间，以及事件所对应空间，再构建不等式组对应几何直观，几何概型定义下，结合几何直观求得随机事件的概率.

三、结语

学科核心素养是学科知识、技能遗忘后，余留下来的并持续发挥作用的东西.学科一般观念的发展，能够有效促进核心素养的提升.“数学的本质是不断抛弃较特殊的概念，寻求较一般的概念；抛弃特殊的方法，寻求一般的方法”.实际上，数学学习的目标不仅在于数学概念、数学定理的积累，更在于形成这些概念和定理背后蕴含的一般观念、一般方法和学科品性.