“猎犬追狐狸”的大学物理解法

李开玮 李振华 刘顺彭

（广东理工学院智能制造学院 广东 肇庆 526100）

1 问题描述

猎犬追狐狸是一个十分有趣的问题，深入研究可以延伸到如何拦截来袭导弹的问题，具有一定的启发意义.猎犬的初始加速度可以通过观察猎犬经过极短时间后，对速度求导得到［1］.更感兴趣的应该是猎犬追上狐狸需要的时间，以及轨迹问题.文献［2］通过构造矢量的乘积并求导，使时间微分前面的系数为常数，再求积分的方法巧妙地求出了追上所需的时间；而文献［3］另辟蹊径通过构造虚力作功的方法，使虚力的功率恒定，虚力的功又能简洁地求出来，这样来得到追击的时间.各有千秋.本文从大学物理的角度，利用运动分解结合定积分的知识探讨猎犬追击时间和轨迹.

如图1所示，一只狐狸以不变速度u沿直线AB逃跑，一只猎犬以不变速率v追击狐狸，运动方向始终对准狐狸，某时刻狐狸在F点，猎犬在D点，相距L，且FD⊥AB，问猎犬追上狐狸需要多长时间？

图1 猎犬追狐狸示意图

2 问题分析

如图2所示，为猎犬运动的大致轨迹图，运动中某时刻，猎犬运动方向与AB夹角为θ，根据图像可知，猎犬与狐狸靠近的速度为v-ucosθ，初始时猎犬与狐狸相距L，当猎犬追上狐狸时，距离为零，设猎犬用时T，因此

图2 猎犬运动轨迹

初始时猎犬与狐狸水平方向距离为零，猎犬追上狐狸时水平方向距离仍为零，猎犬水平方向分速度为vcosθ，因此可得

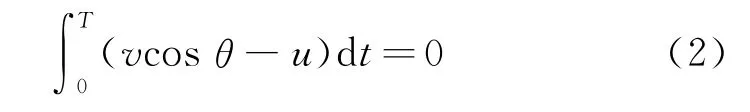
将式（1）两边乘以v，式（2）两边乘以u，相加可得

只要猎犬速率大于狐狸，就一定能追上狐狸.因此猎犬运动路程为

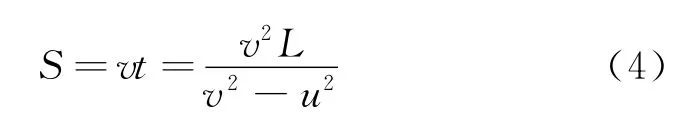
关于猎犬的运动轨迹，建立直角坐标系如图3所示.

图3 坐标系示意图

根据几何图像可得

为方便处理，令cotθ=p，由式（5）可得

式（6）两边对x求导得

3 结束语

通过分析猎犬和狐狸的径向和水平方向的相对速度、距离变化，作定积分，消去角度变量，能够简洁地求出猎犬追击时间，与文献［2，3］结果一致.该问题的中学和大学解法对比可以使学生对大学物理有一个更加深刻的认识，从中学过渡到大学学习阶段.