圆形隧道衬砌内毛细管前端换热器流-热耦合传热模型

范彧菁，胡松涛，张 君，季永明，*

(1.青岛理工大学 环境与市政学院，青岛 266525；2.青岛地铁集团有限公司，青岛 266033)

截止2021年底，中国内地共有45座城市开通城轨交通，运营线路长达7978.19 km，其中地铁占比高达79%[1]。随着地铁的高速建设，地铁运营过程中所带来的高能耗及隧道内废热堆积问题日益凸显。

为解决上述问题，郭红丽[2]提出了基于热泵技术的地铁废热-土壤源混合式热泵系统。胡松涛等[3]在地源热泵技术的基础上，进一步提出了一种将毛细管作为前端换热器的地铁源热泵系统，并对其传热性能进行了大量理论及实验研究。张国柱等[4]建立了内置传统地埋管换热器能源隧道传热模型，并对其传热性能进行了全面分析。因毛细管前端换热器(CHE)支管排布密集，传热均匀，可视为面热源，故传统柱热源和线热源模型并不适用，为此，王依梅[5]提出了一种基于面热源假设的一维平板传热模型，可对敷设于矩形隧道中的CHE传热性能进行预测。

隧道结构中，矩形隧道虽有着空间利用率高的优势，但其受力结构无法满足开挖面大、覆盖深的隧道。圆形隧道受力结构形式良好，且施工自动化程度高，被应用在城市地铁隧道和深埋山岭隧道中，但圆形截面隧道在空间利用上存在一定的浪费。在结合两种隧道结构优势后，马蹄形隧道目前被广泛应用于地铁建设中[6]。

为研究CHE敷设于圆形和马蹄形隧道时的传热性能，本文提出了一种基于面热源假设的一维圆形复合介质传热模型，建立了相应TRNSYS数值仿真模块，并利用实验数据对其预测精度进行了验证。

1 圆形隧道中CHE传热模型

1.1 CHE物理模型

本研究沿用前期研究[3]中假设，将CHE假设为面热源，均匀敷设于地铁隧道一衬及二衬之间；同时为简化模型，假设隧道断面为圆形，忽略CHE沿隧道轴向、圆周方向的传热特性变化。简化后的物理模型如图1所示。

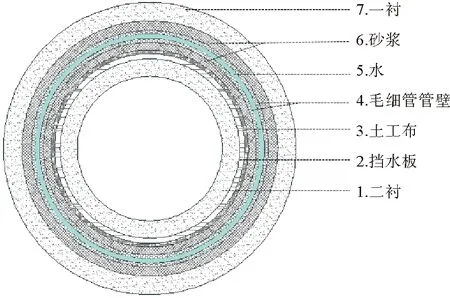
图1 圆形隧道内CHE敷设工法示意

1.2 CHE外围岩温度场传热模型

CHE外围岩传热模型如图2所示。

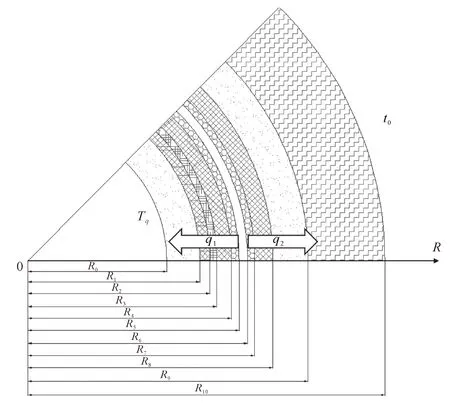
图2 CHE外围岩传热模型示意

地铁源热泵运行时，CHE传热过程遵循能量守恒，可分为3个部分：CHE内循环介质放热量、向隧道围岩深处的传热量和向隧道空气侧(隧道本身)的传热量。以热泵制冷工况为例，CHE传热过程如下：

qz=q1+q2

(1)

q2=qw

(2)

式中：qz为CHE内循环介质的总热流密度，W/m2；q1为CHE内流体与隧道空气侧的热流密度，W/m2；q2为CHE内流体与隧道围岩侧的热流密度，W/m2；qw为作用于围岩表面的热流密度，W/m2。

隧道围岩传热过程为以围岩内表面处(R=R6)为始点，沿隧道径向的一维非稳态导热。为简化模型，作如下假设：

1) 隧道内侧保温层、衬砌、毛细管管壁、围岩各向同性且常物性；

2) 初始时刻，一衬至围岩及围岩外部各处初始温度相同。

则圆形隧道外半无限大围岩传热模型如下[7]：

(3)

边界条件：

(4)

T(R,τ)=t0；R=∞

(5)

初始条件：

T(R,0)=t0；R>R9

(6)

式中：τ为运行时间，s；T(R，τ)为围岩表面温度，K；a为围岩热扩散系数，m2/s；λ为围岩导热系数，W/(m·K)；R9为围岩表面处半径，m；t0为围岩初始温度，K。

对式(3)、式(4)进行拉普拉斯变换并整理得虚宗量贝塞尔方程式：

(7)

边界条件：

(8)

该方程解为

(9)

代入边界条件(5)(8)，在距离隧道无穷远处的围岩温度不可能为∞，借此可确定A和B的数值：

方程解化为

(10)

此时，取R=R9代入解(10)，并进行反拉普拉斯计算[8]，得围岩表面温度场解析解为

(11)

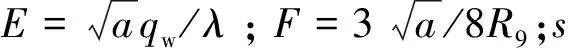
在地铁源热泵实际运行过程中，作用于隧道围岩表面的热流密度qw是随时间而动态改变的，因而恒热流计算模型在实际应用上具有一定的局限性。为了使解析解(11)适用于变热流情况，引入阶跃负荷和叠加原理，对恒热流计算模型进行改进[9]。

将作用于围岩表面的连续变化热流量按照时间步长进行分割，在极短的时间步长内，视传递给围岩表面的热流为恒热流，将每一步长内热流对围岩表面单独的热作用进行叠加，最终可以得到一个近似连续变化热流的总响应。故对于τn时刻末的变热流密度的围岩表面温度解为

(12)

1.3 CHE内流体温度场传热模型

1.3.1 毛细管管内流体传热方程

基于围岩温度场解析解和CHE介质入口温度，可确定CHE管内流体的出口温度。为简化模型，假设如下：

1) 隧道内侧保温层、衬砌、毛细管管壁、围岩各向同性且常物性；

2) 传热过程为准稳态；

3) 忽略衬砌、保温层及围岩等复合结构之间接触热阻；

4) 隧道断面处，CHE内各点流速相同。

基于上述假设，单位时间步长内，传热过程为准稳态。根据变热流密度下的围岩温度场解析解，可得到围岩表面温度Tw。对管内流体应用能量守恒，可得

(13)

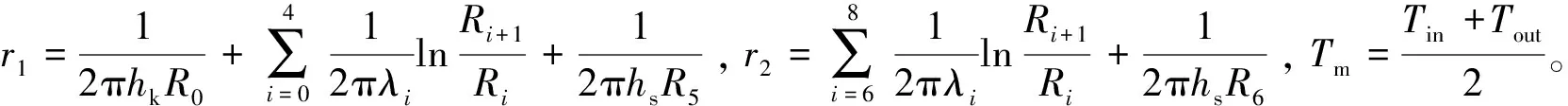
(14)

式中：ρ为CHE内流体密度，kg/m3；c为CHE内流体比热容，J/(kg·K)；v为CHE内流体的体积流量，m3/s；Tm为CHE内流体进出口温度算数平均值，K；Tin为CHE内流体进口温度，K；Tout为CHE内流体出口温度，K；r1为制冷或制热时隧道空气与毛细管网内水流间各介质复合传热热阻，m2·K/W；r2为制冷或制热时毛细管网内水流与围岩表面间各介质复合传热热阻，m2·K/W；Tq为隧道空气温度，K；hk为隧道壁面与空气的对流换热系数，W/(m2·K)；hs为毛细管内流体与毛细管管壁间的对流换热系数，W/(m2·K)；λi为各层材料的导热系数，W/(m·K)；Ri为各层材料距离隧道圆心得半径，m。

1.3.2 CHE管内流体出口温度计算方法

在CHE管内流体入口温度已知的前提下，利用式(12)、式(13)和迭代法对流体出口温度进行求解，过程如图3所示。

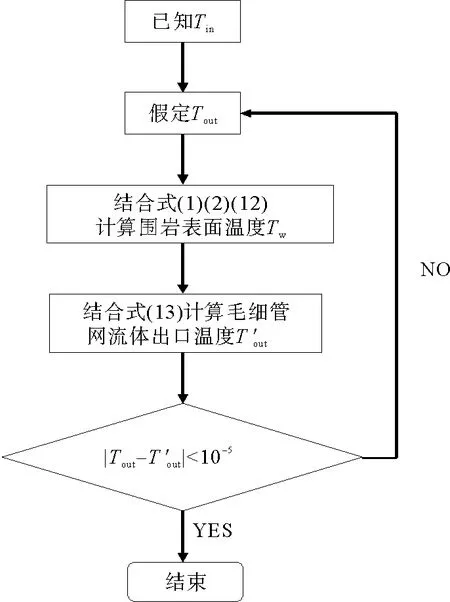
图3 CHE出口温度迭代求解

在过渡季，热泵未运行，CHE内流体静止，则过渡季CHE内流体温度计算模型如下:

(15)

Tm=Tw+qwr3

(16)

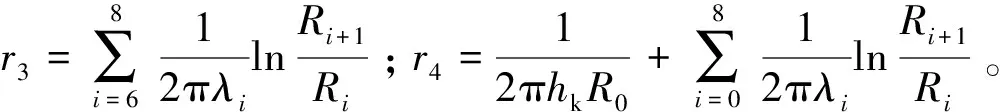
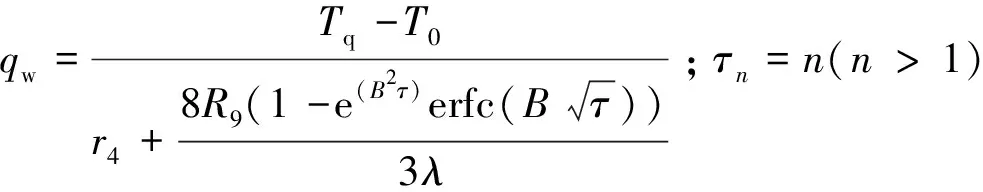
式中：r4为过渡季隧道空气与围岩表面间各介质复合传热热阻，m2·K/W；r3为过渡季CHE内水流与围岩表面间各介质复合传热热阻，m2·K/W；erfc(x)为高斯误差函数。

2 圆形隧道衬砌内CHE流-热耦合模型数值仿真模块

基于上述建立的CHE模型，以代码形式编入TRNSYS模块中，建立相应CHE流-热耦合模型数值仿真模块。

CHE模块在计算过程中存在大量循环，故选用Fortran语言编写源代码，生成.dll文件供TRNSYS识别。供暖季时，由CHE从周边围岩和隧道空气侧取热，空调季传热过程相反；同时，过渡季期间，CHE不开启。

基于上述分类，将代码分为3个部分，利用IF语句进行连接，式(11)中的叠加计算利用DO循环语句实现，完成后模块截面如图4所示。

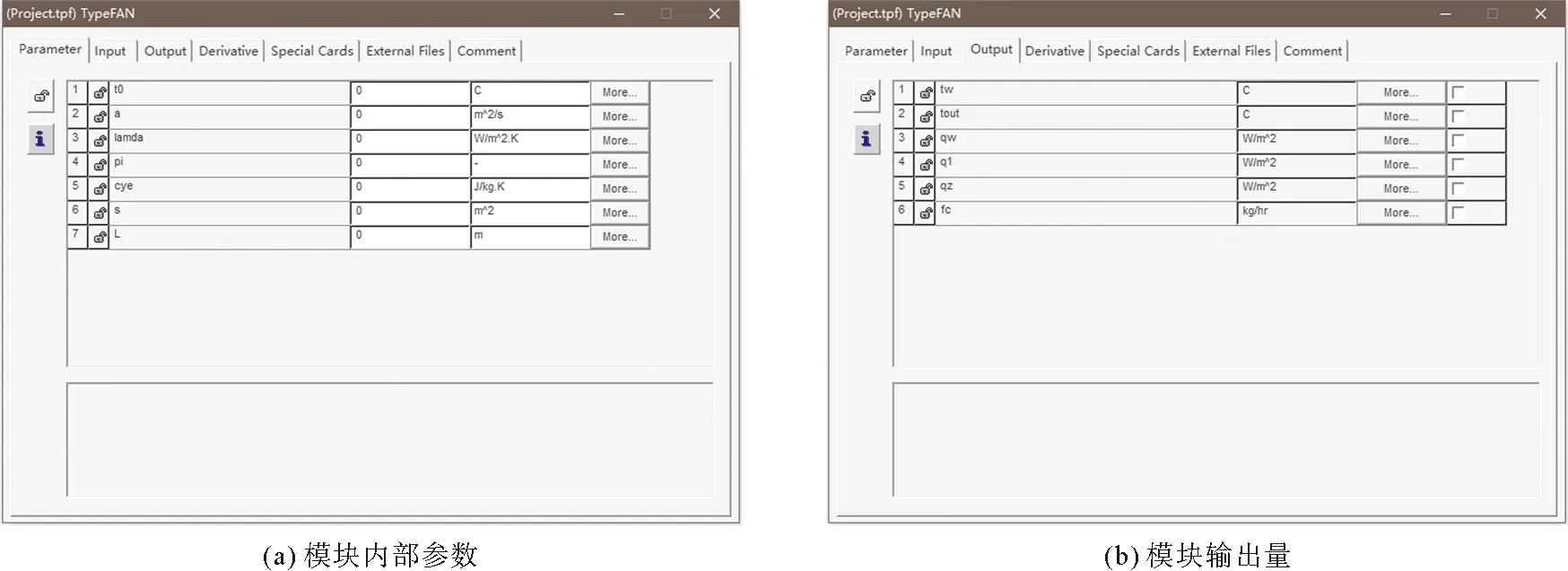
图4 CHE数值编辑模块效果

图4(a)中，t0为围岩初始温度；a为围岩热扩散系数；lamda为围岩导热系数；cye为CHE内液体比热容；S为CHE隧道截面敷设长度；L为CHE沿隧道轴向方向深度。图4(b)中，tw为围岩表面处温度；tout为CHE出口温度；fc为CHE内液体流量。

3 模块验证

本文拟采用在实际地铁隧道中建立的CHE传热性能实验台测试数据，对模型传热特性进行验证。

3.1 CHE传热性能实测

实验地点位于青岛地铁2号线，该站周边隧道段埋深15 m，隧道周围岩体为花岗岩。在该隧道中搭建如图5所示的CHE传热性能实验台。

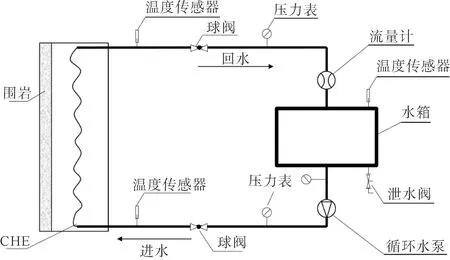
图5 实验测试装置

实验台循环水泵采用封闭转子型水泵，最大扬程为12.5 m；CHE供、回水主管管径为20 mm×2 mm(直径×壁厚)，不锈钢水箱尺寸为360 mm×400 mm×810 mm(长×宽×高)，沿程管路和水箱外均加设30 mm厚的橡胶保温层；水箱内部敷设多根电加热棒，加热量范围为0～4.5 kW。

该实验台中CHE材质采用PPR材料，毛细支管间距按10 mm进行布置，单片毛细管网尺寸为4.5 m×1 m，含毛细支管48根，将毛细管网敷设于图1位置，防水板与二衬共厚300 mm。

测试过程中的相关数据记录由以下设备完成：温湿度自记仪、超声波流量计、铂热电阻温度传感器和多通路数据记录仪。数据记录仪为TP9000多通路数据温度仪，主要负责采集不锈钢水箱内及进出管路中布置的铂电阻测点的测试温度，记录时间间隔为1 min；隧道空气温度利用testo 174H型温湿度自记仪进行记录。温度计及流量计等设备参数如表1所示。

表1 压力表及流量计等设备参数

为模拟地铁源热泵机组间歇运行工况，测试工况如下：流量为0.1 m3/h，水箱内加热器功率调至4.5 kW，采用周期性间歇加热，将水箱内水温加热至39.5 ℃后停止加热，循环水泵持续运行，待CHE进口水温降至35.5 ℃时，加热器再次开启进行加热，如此往复循环，共进行6个周期。

3.2 CHE流-热耦合模型数值模拟

在TRNSYS中搭建如图6所示系统模型，对CHE传热性能进行模拟。

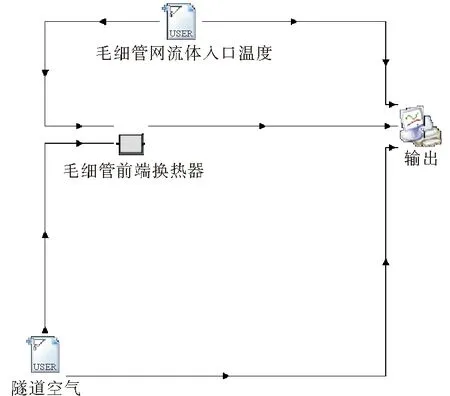
图6 TRNSYS模拟示意

该模型中隧道空气和毛细管内流体入口温度数值取实测值，数据每5 min记录一次，模拟时间步长为0.5 min，模拟结果最终由输出模块导出。各常数参数取值见表2。

表2 各常数参数取值

3.3 结果对比

CHE进出口温度实测及模拟结果如图7所示。

图7显示，系统供水温度在初始阶段迅速上升，达到最高值后迅速下降，如此循环反复，共6个运行循环周期，出口温度的实测值及模拟值变化规律均与供水温度变化规律相同，测试期间，出口温度均低于其模拟值。

CHE出口温度实测及模拟结果逐时相对误差如图8所示。

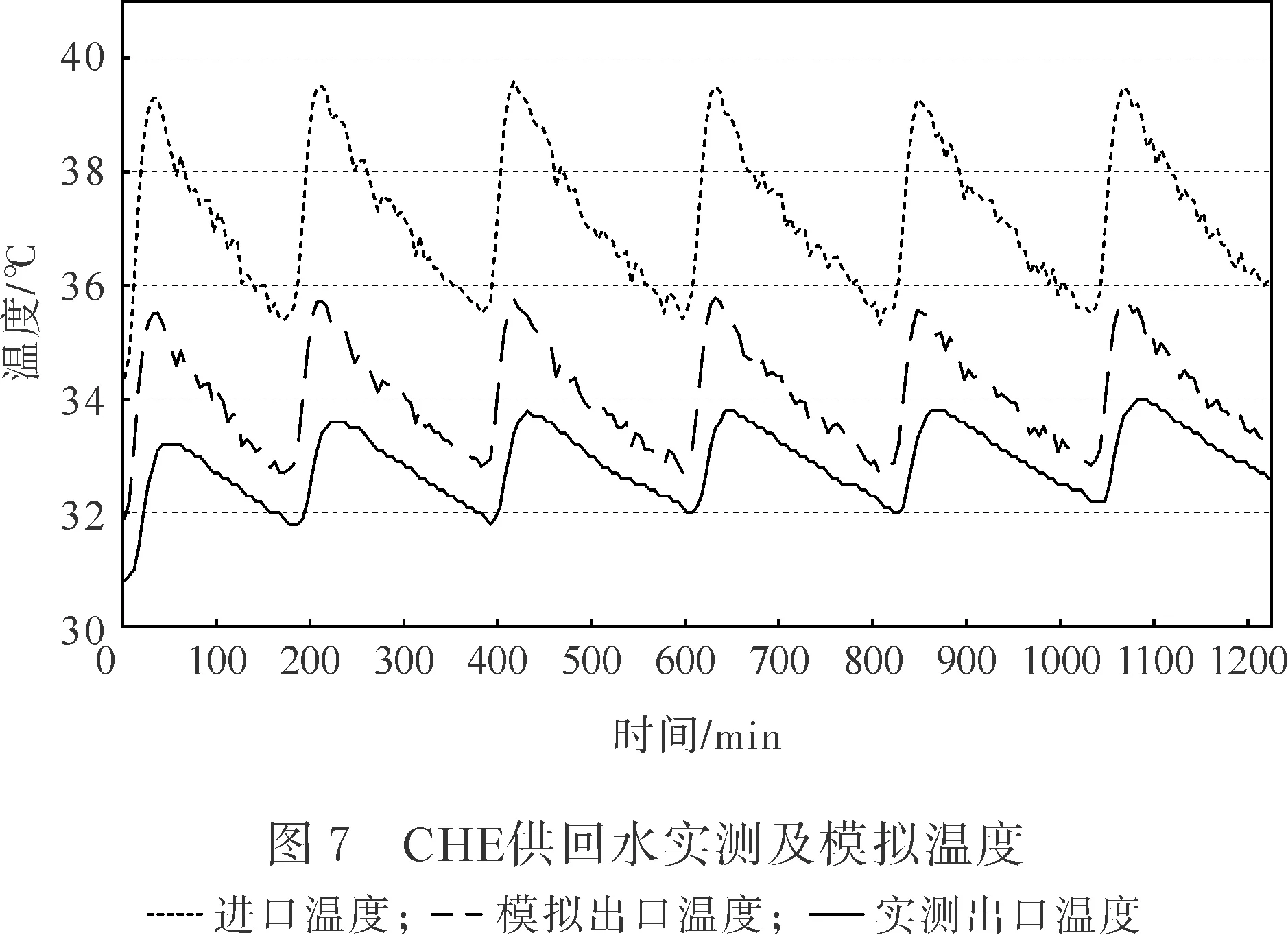
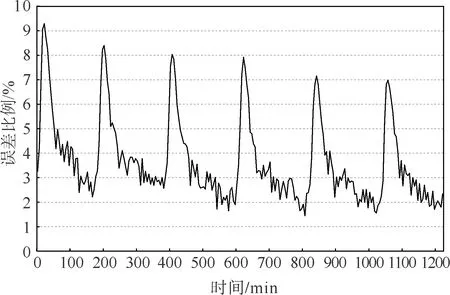
图8 CHE出口温度实测及模拟结果逐时相对误差

图8显示，CHE出口温度实测及模拟结果最大相对误差为9.3%，平均相对误差为3.5%。该工况下共计289个数据点，其中83%的相对误差值在0.2%～5%之间，仅6%的相对误差大于7%。上述结果表明，本研究所建立圆形隧道衬砌内CHE流-热耦合模型数值仿真模块具有较高的预测精度。

在CHE外围岩温度场求解过程中，有如下假设：CHE内流体传热过程处于准稳态。该假设忽略了CHE自身在计算时间间隔内的蓄热性，导致计算温度略高于实际温度。此外，CHE周边复合介质具有一定热容量，导致其温度不会随毛细管管内流体温度和隧道空气温度的变化而发生急剧变化。在各周期起始阶段，水箱内加热器启动，供水温度急剧上升，模拟工况下的毛细管网周边介质温度随之升高，与实际温度温差变大，造成相对误差迅速上升的情况；供水温度达到设定值后，加热器关闭，供水温度下降，模拟工况下的毛细管周边介质温度随之下降，与毛细管周边介质实际温度逼近，相对误差逐步减小。随时间推进，毛细管网周边介质温度整体逐步上升，与模拟工况下的周边介质温度逐步贴近，故而出现后几个循环周期的相对误差均值逐步减小并趋于稳定的情况。此外，材料物性也对结果有较大影响，在模拟时，各层材料厚度均匀，取复合热阻进行计算，但在工程中，材料厚度很难做到各处一样，热阻受厚度变化影响，与设定值会存在一定偏差。上述诸多因素综合作用下，导致本研究CHE流-热耦合模型数值仿真模块与实际相比，依然存在一定的误差，但误差在可接受范围之内，满足实际工程应用需求。

4 结束语

本研究以寒冷地区某实际示范工程为物理模型，通过引入阶跃负荷、叠加原理和拉普拉斯变换等方法，建立了一维圆形复合介质内CHE流-热耦合传热模型，并进一步建立了相应的TRNSYS数值仿真模块。采用实测数据对该数值仿真模块的预测精度进行了验证，结果表明，83%的相对误差值在0.2%～5%之间，最大相对误差为9.3%。表明本研究中所建立的理论传热模型和仿真模块是正确且可靠的。该模型为地铁源热泵系统运行策略优化研究提供了理论基础。然而，本研究模型验证时间较短，工况简单，仍需在更复杂的长期运行工况中对模型进行检验。