刚性固定法焊接工字形钢梁的焊接变形控制
2022-05-07程珂,李军,*,王聪
程 珂,李 军,*,王 聪
(1.青岛理工大学 土木工程学院,青岛 266525;2.青岛城市学院 土木工程学院,青岛 266106)
焊接过程中的不均匀加热和冷却会导致焊接残余变形和残余应力的产生[1],而过大的变形会影响到构件尺寸的精度,甚至形成安装误差,而且还会显著降低结构的承载能力。因此有必要采取有效的措施来控制焊接变形。实际工程中采用的减小焊接变形的方法包括变形后矫正方法和基于一定控制措施使焊后获得较小变形方法两大类。
机械矫正法和火焰矫正法是两种常用的变形后矫正方法。宫平等[2]通过试验研究了机械矫正对焊接接头抗拉强度、冲击韧性、硬度值等力学性能的影响,发现机械矫正量的增加对上述力学性能影响不明显。刘泽毅[3]采用多种加热形式的火焰矫正法对焊接后的水工钢闸门进行了变形矫正,效果显著。
在实践过程中发现,在焊接过程中或焊接前采取一定措施后,变形会得到更有效的控制,例如采用优化焊接顺序和方向、反变形法或刚性固定法等。刘国宁等[4]以T形接头为研究对象,采用焊接模拟方法对比分析了4种不同焊接顺序下的焊接温度场、应变场、应力场,表明焊接顺序可以一定程度上减小焊接变形。所谓反变形方法,即在进行焊接作业时,预先让工件产生与焊接变形相反方向的变形。孙进发等[5]模拟了T形接头在不同反变形量下的变形与残余应力分布,分析表明:施加合理的焊接反变形量可以有效减少焊接变形且不影响残余应力。但在使用反变形法时,由于构件材料、尺寸以及焊接方法等原因导致预加变形量的控制标准难以把握。刚性固定法,即利用刚性比较大的固定件使焊件在焊接时不能移动,等到焊接完全冷却之后拆除刚性固定件,可以使焊接变形相对较小。刚性固定法具有操作简单的特点,但实践中多以经验或等间距适当设置固定件,具有一定的盲目性,应该结合焊接模拟的预测结果进行设置。由于通常认为该法会引起焊接残余应力的增加[6],那么通过合理设置加固位置后焊接残余应力情况如何有待于探明。
本文通过焊接模拟首先预测未做中间加固的构件在焊后的焊接变形情况,提出在最大焊接残余应变处设置固定件的措施,通过加固前后的焊接模拟结果对比,验证所提出方案的有效性,为实际应用提供参考。
1 刚性固定法的实施
在需要加固处设置支撑和夹具,如图1所示,上部采用长筋板焊接或用卡具固定在上翼缘,以有效控制翼缘部位的角变形;腹板处焊缝反面采用三角筋板固定,可有效抑制翼缘的转动,并具有减少钢梁腹板挠曲变形的作用。
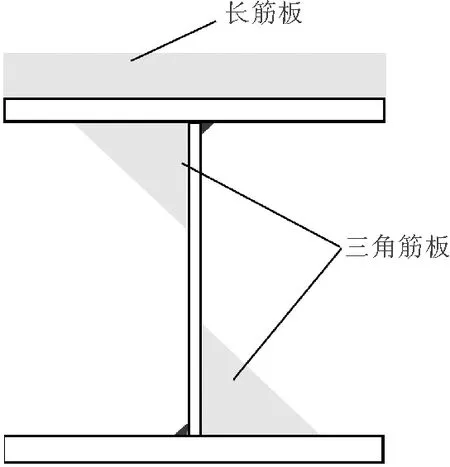
图1 刚性固定法
2 焊接热源模型
ABAQUS软件为用户提供了多种子程序类型,本文利用ABAQUS隐式分析中的DFLUX子程序[7]来定义一个与时间和坐标相关联的热流函数,以此实现焊接过程中移动热源的添加。
焊接热源模型的属性决定焊接温度场的分布规律及焊接后的应力和应变,热源模型的选取对模拟结果至关重要。目前应用比较多的热源模型有点热源模型、线热源模型、面热源模型、高斯热源模型、半球状热源模型以及双椭球热源模型。由于双椭球热源模型可更好地模拟焊接过程中热源前后两部分的不同温度梯度的分布,并具有较准确地反映热源对焊件沿深度方向加热的特点,因此本文采用双椭球热源模型。如图2所示,以x轴为界将模型分成前后两部分,以电弧中心为分界线,前后各由2个长度不同的1/4椭球来表示,该模型前后两部分分别采用不同的表达式来表达。
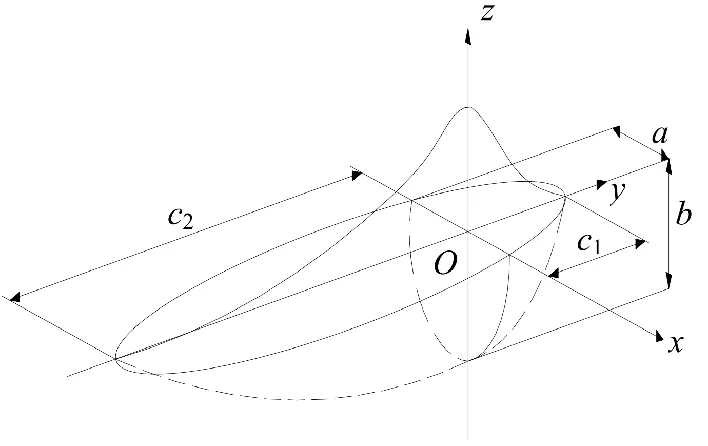
图2 双椭球热源模型
前半部分热源分布的表达式:
(1)
后半部分热源分布的表达式
(2)
Q=ηUI
式中:Q为热源在瞬时给焊件的热能;η为热源效率;U为焊接时的电压;I为焊接时的电流;a,b,c均为焊接模型的形状参数,且相互独立;f1,f2分别为前后部分椭球的能量分数,且f1+f2=2。
3 焊接有限元分析
本文利用ABAQUS的热固耦合分析功能,采用FORTRAN语言编写热源荷载子程序,并在分析模型中调用,以实现对焊接热源的加载。实施顺序耦合,即先进行焊接热分析,再将焊接热分析得到的温度场导入到应力应变场进行热应力分析,最后得到焊接残余应力和焊接残余应变。
3.1 几何模型
本文参考文献[8]中的工字形钢梁截面尺寸,几何参数如下:翼缘宽度260 mm,厚度20 mm;腹板高度240 mm,厚度10 mm。由于本文的目的在于从理论上说明研究结果的有效性,构件长度仅取1000 mm,实际应用宜根据情况建模分析。因为是双轴对称性截面,分析时采用半结构模型。考虑到焊缝余高的存在,在建立焊缝模型时将焊缝简化为1/4圆的形状,取焊脚的尺寸为8 mm。
3.2 单元类型及网格划分
将模型按重要程度依次划分为焊缝及热影响区、过渡区和母材区。因焊缝及热影响区热源输入比较集中,进行网格局部细化。对于过渡区以外的区域利用Structured网格划分方法,使用Hex六面体单元;而过渡区则采用Sweep方法划分网格,用Wedge楔形单元进行过渡。网格模型如图3所示。
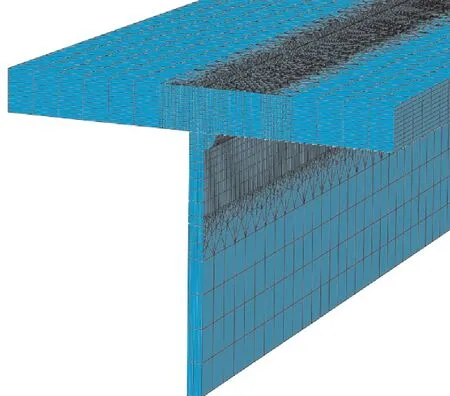
图3 有限元网格模型
温度场分析和应力应变场分析所用到的单元类型不同。温度场分析时所用单元需要具有传热功能且可以进行热分析,故选用热传递单元(DC3D8R,DC3D6);而焊接应力应变场分析时需要计算由不均匀的温度荷载引起的残余应力和残余应变,故选用应力/位移单元中的C3D8R、C3D6单元。
3.3 材料特性参数
焊接热分析的模拟属于非线性瞬态热分析,导热系数、比热容等指标是伴随温度发生变化的,因此需要单独设置。本文所用的工字形钢梁采用Q235B钢材,焊条采用E43型,假设焊缝材料与母材强度相等。焊缝材料性能指标如下:σy=330 N/mm2,E=2.06×105N/mm2,σu=460 N/mm2,εu=0.0012。应力应变场中母材随温度变化的力学参数主要有弹性模量、屈服强度和剪切模量,如表1所示。
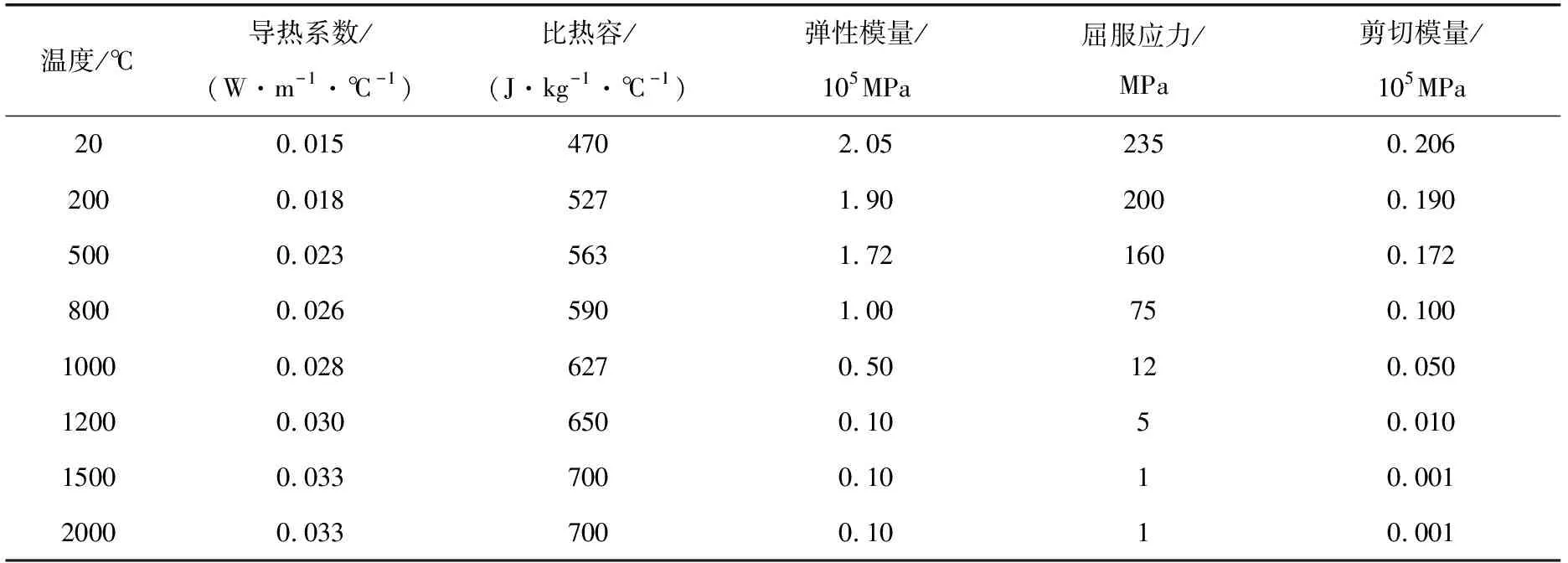
表1 钢材材料性能参数
3.4 约束和边界条件
为更加切合实际中翼缘和腹板焊在一起的情况,在本模型中分3个部件来建模,分别为焊缝、腹板及翼缘,相互接触的部位采用绑定约束(Tie)。在应力应变场分析时,为防止产生过大的变形和移动,在模型的两端添加X,Y,Z方向的固定约束。加固模型的具体做法是除了在两端截面施加3个方向的固定约束外,还在确定最大焊接残余应变所在位置后,将该位置所在截面的自由度耦合到一个参考点上,然后对这个参考点进行侧向位移的约束,以反映长筋板和三角筋板的作用,如图4所示。

图4 加固模型的约束情况
此外还要设置模型与外界空气的对流换热和热辐射作用的参数,本模型取对流换热系数为10 W/(m2·℃),环境初始温度为20 ℃,辐射率为0.85。
4 焊接残余应力分析
4.1 焊接残余应力动态变化
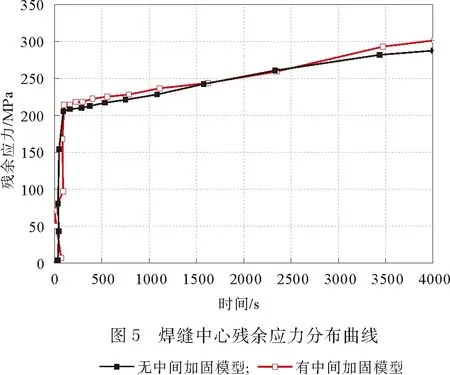
为了研究有中间加固模型残余应力的变化情况,绘制焊缝末端中心位置结点的焊接残余应力动态变化曲线,如图5所示,本文所指的残余应力为等效应力,以下不再特别说明。在热源到达焊缝末端时,无中间加固模型的应力值迅速上升至153 MPa,进入冷却后,残余应力值先迅速上升至204 MPa,然后缓慢上升至最高残余应力值297 MPa;而有中间加固模型开始时应力值不是很大,进入冷却时间段后,残余应力先迅速增长到212 MPa,随后缓慢增加到最大值312 MPa。可见,采用本刚性固定控制方案后,焊接残余应力虽然有所增加,但增加幅度很小,若焊接变形能够得以缓解,这种固定控制方案较为可行,将通过残余应变分析确认焊接变形情况。
4.2 不同路径上的焊接残余应力
为进一步分析有、无中间加固的残余应力分布的差别,采取路径分析的方法对两个模型在同一时间相同路径上残余应力的变化曲线进行对比分析。所选择的3条路径如图6(a)所示。
路径一:焊缝同侧腹板中部位置(沿Z轴方向长度为1000 mm,方向由后向前)。由图6(b)可知,有、无中间加固模型的残余应力分布曲线的形状相似,都呈现出两端高中间低的分布特点。但有中间加固模型的残余应力值整体有所下降;在路径的始端和末端,无中间加固模型的残余应力值均高于213 MPa,而有中间加固模型的残余应力值分别降低到187和135 MPa;在路径中点,无中间加固模型的焊接残余应力值约为25 MPa,加固后降至10 MPa以下。由此可见,对模型的最大变形处采取刚性固定的措施后,可以使腹板长度方向上的残余应力有所降低。
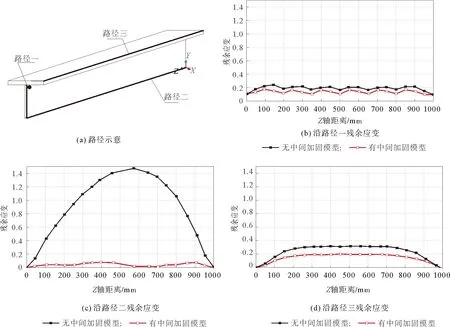
路径二:与焊缝同侧沿腹板高度方向(沿Y轴方向长度为120 mm,方向由下向上),如图6(c)所示,这条路径上随着离焊缝距离的缩小,有、无中间加固的模型的残余应力值都呈上升趋势,但在离焊缝较远处(0 mm 路径三:与焊缝同侧沿翼缘厚度方向(沿X方向距离焊缝50 mm,沿Y轴方向长度为20 mm,方向由下向上)。如图6(d)所示,有、无中间加固的模型的残余应力在该路径上的分布曲线形状基本相似,都呈现出两端高中间低的特点。整体来看,有中间加固模型比无中间加固模型的焊接残余应力均有下降,残余应力最大值和最小值分别由180和57 MPa降低120和46 MPa。可见,对于表面的残余应力值的降低幅度相对要大些。 图6 路径选取及各路径上的残余应力 本文所指的残余应变为等效应变,以下不再特别说明。为了分析有、无中间加固模型残余应变分布的区别,选取沿Z轴方向的3条路径,长度均为1000 mm,具体位置如图7(a)所示。 路径一(焊缝中心位置处):由图7(b)可知,两模型的残余应变都呈波浪线状。有中间加固模型相对于无中间加固模型的残余应变整体下降,无中间加固模型在该路径最高残余应变值为0.237,加固后该路径最高残余应变值降为0.156,下降了近34.18%。但未设加固前该路径的残余应变本身很小,不是焊接变形突出位置。 路径二(焊缝同侧腹板高度方向的中央位置):在该条路径上无中间加固模型残余应变达1.470,是焊接变形突出位置,因这个路径的最大残余应变所在位置出现在模型沿Z方向600 mm处,所以考虑在该处加固,作为有中间加固方案。由图7(c)所知,加固后的残余应变大幅度降低,焊接残余应变最大值降至0.086,效果显著。 路径三(与焊缝同侧的翼缘外边缘上表面位置):由图7(d)可知,两模型在该路径上残余应变的分布非常相似,路径两端的值几乎为零,中间大部分应变值基本呈不变状态。最大残余应变值由0.320降至0.200,下降了37.5%。 图7 路径选取及各路径上的残余应变 本文针对有、无中间加固模型,采用ABAQUS分析软件,基于顺序耦合的分析方法获得两种模型的焊接应力场和应变场,比较分析了两种模型在不同路径下的焊接残余应力和残余应变,主要结论如下: 1) 在可能产生最大焊接变形处设置加固的方案,有效且经济。本文所取构件长度相对较短,故仅在中间位置设置加固即显示出焊接变形显著降低的效果,对于较长构件,需要视实际模拟结果设置加固位置。 2) 本文所取的3条路径上的焊接残余应力,在施加有中间加固措施后都有一定程度降低,但从焊缝中心的焊接残余应力动态变化看,减小焊接残余应变势必会增加个别位置的焊接残余应力。但采用合理的加固方案后,可以将焊接残余应力的增加幅度控制在较小范围内。 本文依据有限元模拟结果进行了讨论和分析,为后续研究提供参考。今后将结合试验并增加构件长度进一步研究。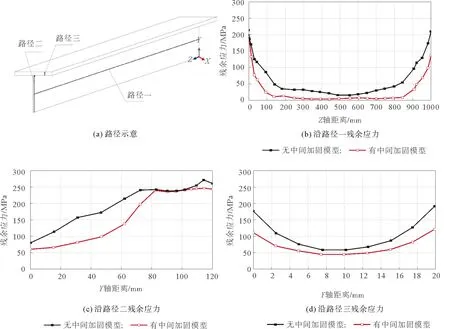
5 焊接残余应变分析
6 结论
