金沙江流域中段森林地上生物量光学遥感估测及饱和点分析

刘关琴，施凯泽，万玉洁，胥 辉

(1. 西南林业大学 西南地区生物多样性保育国家林业局重点实验室，云南 昆明 650224；2. 云南省林业调查规划院，云南 昆明 650051)

森林是陆地生态系统中最大的有机碳储库，对全球碳循环至关重要[1]，评价森林生态系统碳汇能力的其中一个重要指标是森林生物量的分布和变化[2]，森林碳汇估算的关键就在于如何准确估算生物量。传统的野外测量不能提供大规模连续观测数据，且费时费力，遥感模型估测法可以实时、动态、无破坏地对森林地上生物量进行估算，尤其适用于大区域的生物量估算[3]。植被在红外波段和可见光的光谱特征具有明显区别，可利用植被的光谱特征来监测植被生长状况和估测森林生物量，其中，Landsat影像已成为众多学者使用最普遍的遥感数据源[4]，但仍具有不确定性，不确定性的来源主要有生物量模型预估表现、野外样地数据获取、遥感数据源及其空间分辨率、森林的空间异质性、森林生境信息因子等，其中光饱和点的不确定性尤为突出[5]。

近年来，诸多学者对如何解决森林生物量数据饱和带来的问题进行了研究，欧光龙等[6]通过构建不同模型对森林生物量遥感进行估测以探索减少饱和现象造成的估测精度问题。周律等[7]基于遥感变量构建空间回归模型，避免了模型自相关性，提高了思茅松林地上生物量估测精度。许振宇[8]等结合主被动遥感数据，采用4种模型估测分析桂东县森林生物量，为亚热带森林生物量建模分析提供了新思路。

金沙江流域位于长江上游，在云南分布广泛，生态系统十分脆弱[9]。按森林植被类型划分可将此流域分为3个区，东部中山山原峡谷区、中部中山峡谷和滇中高原区、西部高山峡谷区[10]。中部中山峡谷和滇中高原区的主要植被类型为云南松、高山松、针叶林和旱冬瓜、栎类等形成的混交林，此区域缺少相关优势树种光学遥感估测的饱和点数据。目前，其他地区已有对这些优势树种光学遥感估测饱和点的探索结果，卢腾飞等[11]利用三次模型拟合曲靖市云南松生物量饱和值为167 t/hm2。赵盼盼[12]估算浙江省中西部针叶林的生物量饱和值得到马尾松与杉木遥感生物量估测饱和值分别为159 t/hm2和143 t/hm2。吴勇等[13]通过皮尔逊相关系数比较筛选出Landsat 8 OLI Band 4波段变量与AGB进行曲线拟合，求得高山松林与云冷杉林遥感生物量估测饱和值分别为149.09 t/hm2和162.3 t/hm2。

基于此，将以云南省金沙江流域中段的5类主要树种为研究对象，基于Landsat 8 OLI遥感影像，结合地面二调小班数据，构建生物量估测模型，探索光学遥感数据源的饱和点阈值确定方法，并反演研究区5类主要树种的地上生物量。实现对研究区生物量估算精度的提升，减小因存在数据饱和问题所造成的不确定性。为进一步提高大尺度流域生物量光学遥感估测精度提供理论依据，为今后金沙江流域森林碳汇计算提供理论基础，也为其他流域的森林生物量光学遥感估测及饱和点分析研究提供参考。

1 研究区概况

金沙江流域发源于青藏高原，流域全长1 560 km，介于25°～36°N和90°～103°E范围，流域内地形极为复杂，众多高山峡谷相间并列，地势北高南低，落差约5 100 m。各区段自然环境差异较大，有明显的垂直气候特征[14]。研究区域位于大理、丽江、楚雄3个州市所在的金沙江流域，本文中统一称为金沙江流域中段(图1)。

2 研究方法

2.1 数据来源及处理

2.1.1小班数据

1)小班单位面积地上生物量计算

选取研究区2016年森林资源二类调查小班数据，包括金沙江流域流经的楚雄、大理、丽江3个州市。根据实际情况，本研究选取云南松林、常绿栎类林、高山松林、其他阔叶林、其他针叶林进行分析建模(表1)。参考胥辉等[15]的蓄积量—生物量转换模型计算各小班单位面积森林生物量[16]。计算公式为：

B=V×SVD×BEF

(1)

式中：B为小班单位面积地上生物量(t/hm2)；V为小班单位面积蓄积量(m3/hm2)；SVD为基本木材密度(t/m3)；BEF为生物量转换因子(无量纲)。

2)样本小班的确定

优势树种或树种组在研究区分布如图1B所示，将小班中的异常数据剔除，筛选出平均胸径大于等于5 cm的小班；利用 ArcGIS“子集要素”工具，等比例保留小班数据；再利用三倍标准差法删除异常离群值，最终选出4 144个小班样地，其中分别取70%小班进行建模，30%小班作为检验样本，具体信息如表2所示。

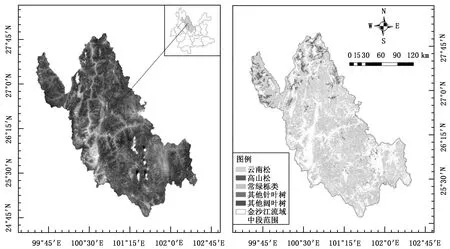
(a)金沙江流域中段Landsat 8 OLI合成遥感影像 (b)金沙江流域中段各树种或树种组分布

表1 生物量转换因子法计算模型Tab.1 Calculation model of biomass conversion factor method

2.1.2遥感影像数据

在地理空间数据云网站下载与二类调查数据同时期的流域区域的Landsat 8 OLI卫星影像数据(表3)，利用ENVI 5.3进行辐射定标、FLAASH大气校正、地形校正预处理，进而通过影像融合、裁剪及镶嵌获得研究区预处理后的遥感影像数据。

2.1.3遥感因子提取与筛选

以云南松林、常绿栎类林、高山松林、其他阔叶林和其他针叶林的小班面状数据为单位，将小班面状矢量数据和134个遥感特征因子数据层相叠加，统计小班内各遥感因子的平均值[18]。本研究提取的4类遥感因子分别如下：

表2 小班样地的选择Tab.2 Selection of subcompartment plot

表3 研究区Landsat 8 OLI影像基本信息Tab.3 Basic information of Landsat 8 OLI images in study area

1)原始单波段[17](7)：B1、B2、B3、B4、B5、B6、B7；

2)植被指数[18](9)：ARVI、B、DVI、G、MSAVI、NDVI、PVI、RVI、SAVI；

3)K-T和K-L变换因子[18](6)：KT1、KT2、KT3；PCA1、PCA2、PCA3；

4)纹理特征[18](3*3、7*7，112)：Mean、Variance、Homogeneity、Contrast、Dissimilarity、Entropy、Second Moment、Correlation。

2.2 生物量与遥感变量的相关性分析

研究采用皮尔逊相关系数分析，SPSS 软件对生物量与各遥感变量进行相关性分析，选择相关显著性(P≤0.05)的遥感因子作为建模备选变量。

2.3 生物量光学遥感估测的光饱和点确定

根据地上生物量与各波段光谱反射率相关性，选择生物量与相关性最为显著的波段反射率做散点图，发现波段反射率会随生物量的增大逐渐减小，当生物量达到一定水平时波段反射率不再发生变化，该临界值即为光学遥感估测生物量时的饱和点。为进一步量化云南松林、常绿栎类林、高山松林、其他阔叶林和其他针叶林的生物量饱和值，通过拟合生物量与波段反射率的函数关系，计算函数所对应的拐点值确定生物量遥感估测的光饱和点值。

2.4 模型构建

2.4.1线性回归模型构建

运用IBM SPSS Statistics 22对遥感因子进行相关性分析，筛选出显著性较好的因子，自变量为遥感因子，因变量为单位生物量，以IBM SPSS Statistics 22为平台，建立线性逐步回归模型，其公式为：

Y=β0+β1x1+β2x2+…+βnxn+ε

(2)

式中：Y为生物量;β0为常数项;β1，β2…βn为模型系数;x1，x2…xn为相关遥感因子;ε为模型满足随机正态分布下的随机残差;n为自变量个数。

运用SPSS进行多元线性回归，输入观测值即单位生物量、自变量即相关性较显著的遥感因子值，输出结果包括非标准化系数、标准误差、标准系数、t、Sig、VIF。在变量间的多重共线性问题极其常见，且对模型造成严重影响，用VIF函数对自变量进行共线性检验。

2.4.2KNN模型构建

KNN算法能用于森林参数的估计和各种空间数据的因变量估测，通过计算K个样本点特征空间中最邻近参考像元的属性并计算其反距离权重平均值得到未知像元点的属性。一般情况下，训练样本点的影像随距离的增加逐渐减小。本文主要采用欧氏距离，计算公式为：

(3)

式中：ρ为点(x2，y2)与点(x1，y1)之间的欧氏距离；|X|为点(x2，y2)到原点的欧氏距离。

2.4.3模型独立性检验

选取决定系数(R2)、平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)和相对均方根误差(rRMSE)5个指标作为模型的独立性检验指标。公式为：

决定系数(R2)：

(4)

平均绝对误差(MAE)：

(5)

平均相对误差(MRE)：

(6)

均方根误差(RMSE)：

(7)

相对均方根误差(rRMSE)：

(8)

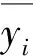
2.4.4“刀切法”残差分析

残差是观测值与回归值的差，其通过模型的拟合效果对模型预测结果产生影响。通过“刀切法”残差分析对研究区5类优势树种或树种组和总体样本分别进行划分区间，计算分析区间模型残差情况，确定模型在遥感估测中是否存在误差。采用3个指标作为“刀切法”残差结果评价指标，分别是平均残差(ME)和平均相对残差(MRE)，计算公式为：

(9)

式中：n为样本总数；yi为实测值；y^i为估测值。

3 结果分析

3.1 生物量光学遥感估测饱和点的确定及分析

图2表示5类优势树种或树种组的遥感因子散点图和饱和点拟合曲线。由曲线趋势可以看出，5类优势树种或树种组的单波段遥感因子值随其单位生物量的增加而逐渐趋于一个固定值，这个值所对应的单位生物量即为各树种的饱和点。利用饱和点曲线的二项式方程计算得出云南松林、常绿栎类林、高山松林、其他阔叶林、其他针叶林的饱和点分别为 98.870 t/hm2、101.220 t/hm2、 127.938 t/hm2、88.432 t/hm2、160.201 t/hm2；R2分别为0.471、0.325、0.232、0.336、0.312。

3.2 生物量模型拟合与评价

3.2.1生物量与遥感因子相关性分析

筛选出5类优势树种或树种组，并将这5类优势树种或树种组的遥感因子的均值统计量与生物量进行Pearson’s相关性分析，将相关性高的遥感因子进行多重共线性诊断，选取方差膨胀因子VIF<10的遥感特征变量，最终得到的结果见表4。

3.2.2模型拟合

1)线性回归模型构建

5类树种或树种组参与逐步线性回归模型构建的遥感因子之间的线性关系见表5。

从表5可以看出，各树种或树种组与参与模型构建的遥感因子之间的线性关系，众多遥感因子中纹理特征被纳入建模次数较多，存在较好的相关性，其中COR7_1、SM7_4分别被不同的3个树种或树种组纳入3次，而K-T和K-L变换因子仅被其他阔叶林和其他针叶林纳入一次建模，表明这类遥感因子与这5类树种或树种组的生物量相关性不强。不同树种或树种组的R2也各不相同，其他针叶林的R2最高，为0.356；其次是其他阔叶林的R2，其值为0.344，且RMSE最低，为5.190，表明此模型对于这两类树种的地上生物量具有最好的模型拟合效果；常绿阔叶林、高山松林的R2均在0.2以上，且RSME值均相对较低，表明模型对这几类森林的生物量具有较好的模型预估精度；云南松林的R2只有0.112，模型拟合精度最低，表明多元逐步线性回归模型对于计算该地区的云南松林生物量的适用性不强。

图2 5类优势树种或树种组饱和点拟合曲线Fig.2 Fitting curve of saturation point for five dominant tree species or species groups

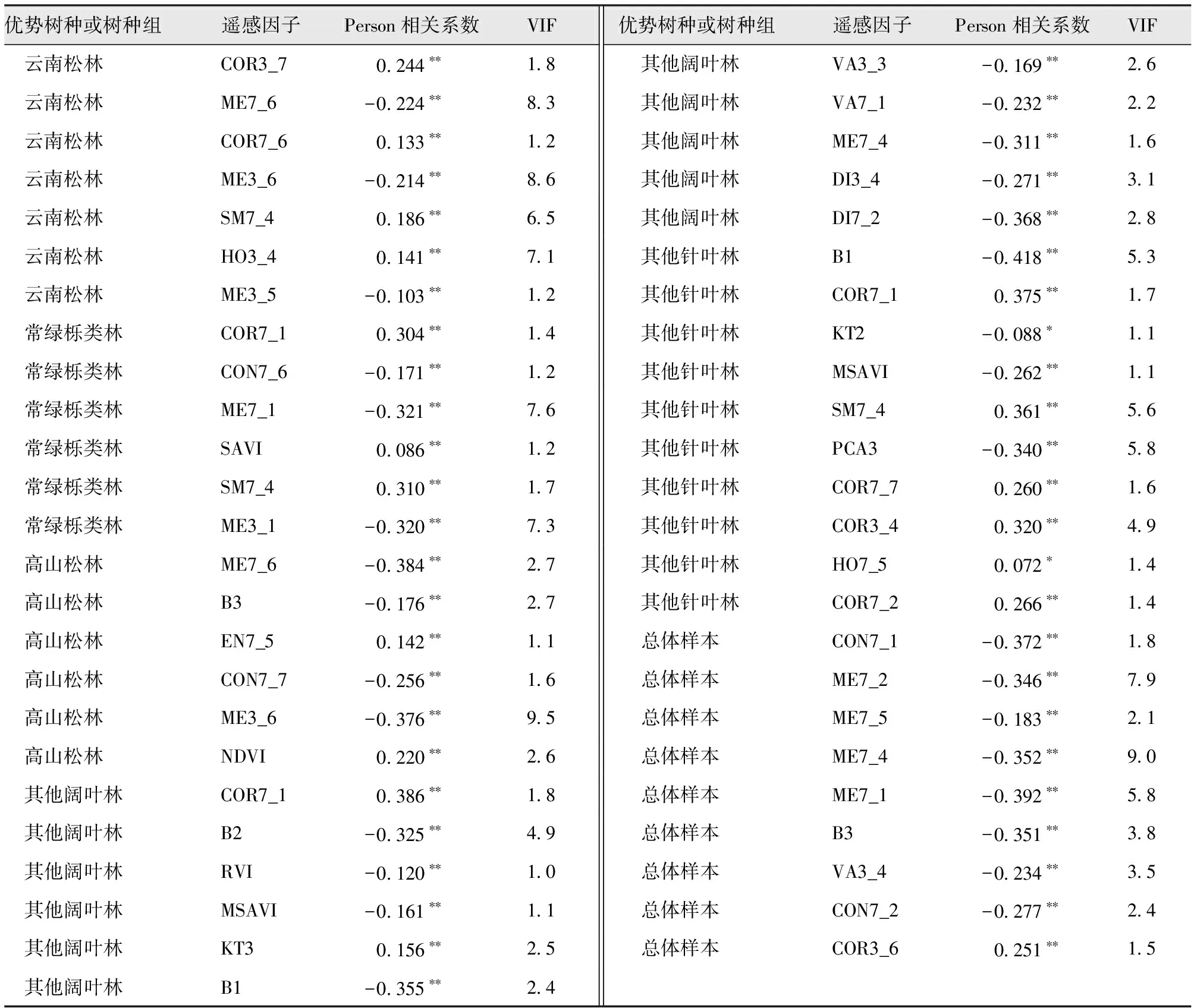
表4 5类优势树种或树种组的相关性分析及共线性诊断Tab.4 Correlation analysis and collinearity diagnosis results of five dominant tree species or species groups

表5 5类树种或树种组逐步线性回归模型构建Tab.5 Construction of stepwise linear regression model for five dominant tree species or species groups

2)KNN模型构建

KNN模型以线性回归筛选的遥感因子为自变量，以单位生物量为因变量，对各树种进行建模，就决定系数(R2)来讲，有4个模型达到0.3以上，其他针叶林最高为0.416；从均方根误差(RMSE)来讲，其他阔叶林模型最低为5.110，总体来看KNN模型的拟合效果更好一些(表6)。

表6 KNN模型精度评价结果Tab.6 KNN model accuracy evaluation results

3.2.3模型检验

总体来看，估测模型中总体平均相对误差、平均绝对误差和相对均方根误差基本上是KNN算法表现的最低，而决定系数KNN算法表现的最高(表7)。因此，选择KNN作为云南省金沙江中段遥感估测的最终模型。

表7 线性逐步回归模型和KNN模型独立性检验Tab.7 Independence test results of stepwise linear regression model and KNN model

3.2.4“刀切法”残差分析

通过分段残差分析，整体上KNN模型的预估精度较高，误差相对逐步回归模型较小。从生物量分段看，两个模型均存在生物量低值高估和高值低估情况，其他阔叶林只有<50 t/hm2生物量段，且均为高值低估；在低生物量段(<50 t/hm2)时，除其他阔叶林和逐步回归模型估测的其他针叶林的MRE为正值外，其余均为负值。在(>50 t/hm2)生物量段时，均为正值，且ME和MRE随生物量段的增加呈增大趋势，直到(>150 t/hm2)生物量段时，常绿栎类林和高山松林的ME均大于90 t/hm2，且MRE值均大于1，出现显著的高值低估情况，说明在高生物量段两模型估测能力均显不足(表8)。

4 讨论与结论

4.1 讨论

遥感影像的各特征变量均是对森林生物量特征及其变化的响应，但普遍存在当生物量增大到一定程度时遥感信息发生饱和的现象，这一问题已成为影响生物量估测精度的主要原因，进一步研究解决遥感数据估测森林生物量普遍存在的数据饱和问题十分迫切。由于林木生物量中58%由树干部分构成，而植被在生长最为繁茂的季节，其树干部分的信息被表层树冠掩盖，导致传感器记录的信息不完整，因此出现了以Landsat 8_OLE数据为数据源的生物量估测在高密度地区以及森林结构复杂地区容易出现饱和点问题[19]。

表8 “刀切法”残差分析Tab.8 Residual analysis using Jackknife method

本文以Landsat8_OLI遥感影像为主要数据源，结合森林资源规划设计调查统计数据，探索参数模型(逐步线性回归)和非参数模型(KNN)两种算法在云南省金沙江流域中段森林生物量遥感估测中的不同效果，通过对比两种建模方法在生物量估测中的效果，选择适合的模型，实现对云南省金沙江流域中段森林中5类优势树种或树种组的生物量遥感估测，并就生物量估测中普遍存在的饱和点问题进行定量分析比较。研究区样本生物量饱和值为：其他针叶林(160.201 t/hm2)>高山松林(127.938 t/hm2)>常绿栎类林(101.220 t/hm2)>云南松林(98.870 t/hm2)>其他阔叶林(88.432 t/hm2)，该值低于赵盼盼[12]研究所得的森林生物量光饱和值(马尾松林159 t/hm2；杉木林143 t/hm2；阔叶树林123 t/hm2)，这可能是因为生物量光饱和点受多种因素影响，云南省金沙江流域中段山地地形复杂，立体气候明显，垂直高差大，且林分结构繁复，森林异质性水平更高。

合适的建模方法可以在一定程度上减小数据饱和的影响，逐步性线回归模型和KNN模型已成为遥感估测森林生物量常用方法，从模型独立性检验来看，KNN模型下各优势树种或树种组的R2都比逐步性线回归模型下的高，表明KNN模型的估测精度高于逐步线性回归模型的估测精度，这与戚玉娇[20]、郭颖[21]、韩宗涛[22]等的研究结果一致。从不同的生物量分段结果来看，两个模型均存在低值高估和高值低估情况，但总体上，不同优势树种或树种组在所有生物量分段上的ME和MRE均表现为KNN模型优于一般逐步线性回归模型，可见KNN模型有着更为精确的模型估测能力，且在一定程度上能够减小数据饱和引起的估测误差，但当生物量段>150 t/hm2时，常绿栎类林和高山松林的ME均大于90 t/hm2，且MRE值均大于1，出现显著的高值低估情况，说明在高生物量段两模型估测能力均显不足。

本研究利用半变异函数求解森林生物量光饱和值为流域森林生物量光饱和值求解提供了一定的参考，且对比分析了逐步线性回归和KNN模型，结果表明，KNN模型在一定程度上提高了生物量的估测精度，但与实际值对比仍然具有明显的高值低估情况。由于本研究所选取的遥感变量因子较为单一，模型的选取也只考虑了KNN模型和逐步线性回归模型，然而实际的生物量估测还受其他环境变量因素的影响。建模过程中影响因素众多，各种方法各有优势，每种方法的适用均存在一定的局限性，只能根据数据客观条件优选某一种或多种方法，今后的研究可以结合多元遥感数据，考虑更多的遥感变量和环境因子以及森林信息来估测森林生物量进而提高估测精度。

4.2 结论

通过对5类树种或树种组进行函数求解，参数方程组合，求出各树种或树种组的光学遥感估测生物量光饱和值：其他针叶林160.201 t/hm2，高山松林127.938 t/hm2，常绿栎类林101.220 t/hm2，云南松林98.870 t/hm2，其他阔叶林88.432 t/hm2。

逐步线性回归模型和KNN模型对森林生物量均具有较好的估测能力，其中，KNN模型的估测精度及拟合效果明显优于逐步线性回归模型。生物量残差分段分析表明，两模型均存在低值高估和高值低估的情况，且在低生物量段(<50 t/hm2)时，除其他阔叶林和逐步线性回归模型估测的其他针叶林的MRE为正值外，其余均为负值。在(>50 t/hm2)生物量段时，均为正值。在中、低生物量段(<100 t/hm2)时，KNN模型预估精度高于逐步线性回归模型，在高生物量段(>150 t/hm2)时，两种模型的预估精度均不高。整体来看，KNN模型的预估精度远高于逐步线性回归模型。