基于GWO-P&O算法的局部阴影光伏MPPT研究

沈 磊， 徐岸非， 黄晴宇， 余嘉川

(湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，湖北 武汉 430068)

利用MPPT技术尽可能获得光伏阵列最大输出功率是提高光伏发电效率的有效手段[1]。在均匀光照下光伏阵列的输出功率—电压曲线呈现出单峰值特性[2]，电导增量法、扰动观察法等传统MPPT控制方法均可快速搜寻到最大功率点，然而实际的光伏系统工程通常分布在工业园区、居民区等建筑较为密集的区域，周围的一些建筑物和树木会遮挡住部分光伏组件，造成局部阴影现象，光伏阵列的输出功率—电压曲线会出现多个局部峰值和一个全局峰值。此时，传统的最大功率追踪方法往往会陷入局部最优而失效。因此，针对局部阴影下的MPPT控制进行研究具有重要的实际意义。

近年来，为了解决上述问题，国内外学者进行了大量研究，提出了一系列优化算法来缓解局部阴影对光伏阵列输出功率的影响，大多集中于智能算法在MPPT上的应用[3]。王红艳等[4-6]提出了粒子群算法及其改进算法在MPPT上的应用，在不同阴影条件下能够很好地追踪到最大功率点，但是其结构较为复杂。于新[7]采用了一种基于变步长萤火虫算法的MPPT方法，一定程度上提高了MPPT的搜索能力和收敛速度。除此之外，基于模糊逻辑控制(FLC)、人工神经网络(ANN)、遗传算法(GA)和蚁群优化算法的MPPT控制方法也取得较好的效果[8]。但均存在算法调节参数多、结构复杂等问题。

粒子群算法依赖于最优粒子和个人经验的指导作用，在迭代后期极易出现算法多样性下降和过早收敛，此时依然存在陷入局部最优的可能性。相比之下灰狼算法具有参数少、搜索精度高的特点，其中存在收敛因子和随机权重因子，能够实现全局搜索，在提高求解精度方面具有良好的性能，被广泛地应用于电力、能源调度等工业控制领域。Satyajit Mohanty[9]等人首先将其应用到了MPPT控制策略中，但由于灰狼算法随机权重的搜索策略使得该算法在寻找最大功率点过程中收敛速度还有待提高。本文在分析局部阴影下光伏特性曲线的基础上，提出了灰狼算法和扰动观察法相结合的复合算法，采用直接占空比控制。Matlab/Simulink仿真结果显示，该算法兼顾两者的优点，具有较强的综合性能。

1 局部阴影下光伏阵列建模及仿真

1.1 局部阴影下光伏阵列建模

均匀光照条件下，多个光伏组件串并联构成一个Ms×Np的光伏阵列的输出特性[10]为

(1)

其中V、I分别表示光伏阵列的输出电压和输出电流；Voc、Isc分别为光伏阵列的开路电压和短路电流；C1、C2为光伏电池的结构系数。但是不同于均匀光照下的光伏特性，当光伏组件发生局部阴影现象时，其并联的旁路二极管会出现阻断和导通两种状态，这时式(1)将不再适用。采用分段函数来表示光伏阵列的特性[11]。为了便于说明，首先简化光伏阵列的结构，构建如图1所示的3个光伏电池串联的单串光伏阵列。

图 1 串联光伏阵列模型

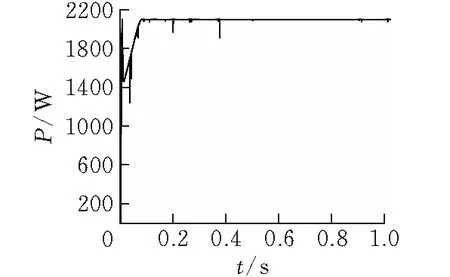
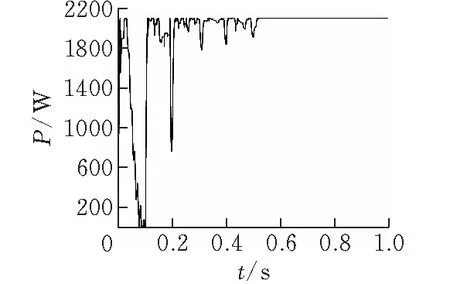
由图1可知PV1处于正常光照，PV2和PV3被部分遮挡，处于局部阴影下，其中PV3遮挡比PV2严重。由于光伏阵列的短路电流和光照强度是正相关的，所以PV1、PV2和PV3的短路电流满足Isc1>Isc2>Isc3。当光伏阵列输出电流满足Isc2

(2)

进一步归纳可以得到任意阴影条件下Ms×Np的光伏阵列数学模型为

(3)

V=max{Vi}

(4)

式(3)和式(4)中，Ii、Vi表示单个光伏电池的输出电流和电压。

1.2 局部阴影下光伏阵列仿真

为了更加直观地分析不同阴影条件下光伏阵列的输出特性，在Simulink中搭建了5×2的光伏阵列模型。考虑到实际应用情境下，光伏阵列受到的辐照度会因为建筑、乌云等遮挡有明显的变化，但在一定范围内温度的变化并不会太剧烈。本文以光照强度变化100 W/m2，温度变化1℃为宜，也符合实际工况。不同光照条件下的光照及温度参数见表1，不同条件下光伏阵列对应的P-V曲线见图2。

表1 不同阴影条件下光伏阵列光照及温度参数

图 2 5×2光伏阵列在不同阴影条件下的P-V曲线

由图2可知，在均匀光照条件(STC)下，光伏阵列输出的P-V曲线只存在单峰值；在PSC1条件下，光伏阵列受到2种不同强度的光照，其存在2个峰值点。在PSC2条件下，光伏阵列受到3种不同强度的光照，存在3个峰值点。但是，三种条件下均只有一个全局最大功率点。因此光伏阵列在局部阴影下的P-V曲线呈多峰特性，具有一个全局峰值和多个局部峰值。光伏阵列受到光照强度的类别越多，其峰值点也就越多。在此场景下，研究全局寻优的MPPT算法具有重要意义。

2 基于灰狼算法和扰动观察法的MPPT算法

2.1 灰狼算法在MPPT上的应用

灰狼算法是 Mirjalili[12]等人于2014年提出来的群智能算法，它是基于灰狼捕猎行为而开发的一种全局寻优算法。建立灰狼寻优的数学模型的过程如下：

1)社会等级分层：将狼群按照适应度大小分成 4 组，分别为α、β、δ、ϖ四个等级。每只灰狼的位置都表示寻优问题的一个潜在解，其中α狼是适应度最好的狼，其对应的位置是所有解中最优解，β、δ狼分别次之，ϖ狼代表其它解。

2)包围搜索猎物：灰狼算法的实质就是高等级狼指挥低等级狼向猎物接近并包围的行为。其搜索行为可以用式(5)和(式6)表示。

D=|C·Xp(i)-X(i)|

(5)

X(i+1)=Xp(i)-A·D

(6)

式中，D表示狼与目标的距离向量，i表示当前的迭代次数，Xp表示目标可能出现的位置向量，X表示搜寻过程中灰狼的位置向量，A、C为协同系数向量，由式(7)和式(8)计算得到。

A=2a·r1-a

(7)

C=2r2

(8)

式中，r1、r2表示[0,1]的随机数，a为收敛因子，随着迭代次数的增加，由2线性递减到0。

3)狩猎：当完成包围后，狼群开始狩猎，接着在每次的迭代过程中，保留适应度最好的三只狼，根据α、β、δ三狼的位置对狼群的位置进行更新。逐渐向猎物逼近，更新过程如下：

Dα=|C·Xα(i)-X(i)|

(9)

Dβ=|C·Xβ(i)-X(i)|

(10)

Dδ=|C·Xδ(i)-X(i)|

(11)

X1=Xα(i)-A·Dα

(12)

X2=Xβ(i)-A·Dβ

(13)

X3=Xδ(i)-A·Dδ

(14)

X(i+1)=(X1+X2+X3)/3

(15)

式(9)—(15)中Xα(i)、Xβ(i)、Xδ(i)表示当前种群中α、β、δ位置，Dα、Dβ、Dδ分别为ω群个体与α、β、δ位置的距离，X(i)表示灰狼当前位置向量，X1、X2、X3表示ω群个体向α、β、δ狼前进的步长和方向。X(i+1)表示ω群个体更新后的位置。

4)攻击猎物：狼群在完成上述行为后，通过攻击来完成狩猎。为了更加直观的表示逼近猎物的过程，式(7)中的a的值逐渐减小，A的波动范围亦随之减小。即在迭代过程中，当a的值从2线性下降到0时，A的值在[-a，a]范围内波动，此时灰狼的更新的位置可以是其当前位置和猎物之间的任意位置点。|A|<1时，狼群攻击猎物(局部最优)，|A|>1时，使狼群远离猎物，寻找更合适的猎物(全局最优)。除此之外，该算法还依靠另一个向量系数C来进行全局搜索。由式(8)可知C为[0,2]的随机向量，表示狼群个体位置对猎物的随机影响权重。这样在使用式(9)-式(11)计算距离时，随机的减少(|C|<1)或者增强(|C|>1)对猎物的影响权重。这种优化过程中的随机行为，有利于全局搜索和避免局部最优。值得一提的是，C与a相比并不是线性递减的。而是在任何时候都提供随机值，这样一来，从初始迭代到最终迭代，C均提供了全局搜索策略，在陷入局部最优情况下，其随机性对跳出局部最优非常有用。

将上述灰狼算法应用于MPPT控制，采用直接占空比控制，以狼群个体的位置表示Boost电路的占空比D。以光伏阵列的输出功率P=Vpv×Ipv作为目标函数，目标函数即适应度函数，它是判定灰狼个体等级的标准。

在灰狼狩猎过程，将适应度最好的灰狼α，β，δ的位置保留，并引导适应度低的狼向猎物方向靠近。通过不断的迭代逼近最优解所在的位置，当迭代次数达到最大值或者功率变化小于阀值时，α狼所在的位置即最大功率点对应的占空比，此时占空比将会是一个恒定值。

2.2 扰动观察法在MPPT上的应用

扰动观察法是最普遍的一种MPPT控制方法，也是众多新型MPPT控制算法的重要参照[13]。其主要分为两步，第一步设置一个扰动步长，和灰狼算法相同采用占空比控制Boost电路，采用基于功率变化的占空比扰动，即在间隔一个采样周期后，以一个固定的占空比步长增大或减小占空比的值；第二步比较扰动前后光伏电池输出功率的变化情况，如果输出功率增加，就进行同向扰动，反之，进行反向扰动。在经过了多次扰动后，即可达到最大输出功率或者围绕最大功率小幅度震荡。

扰动过程可以以式(16)和式(17)表示。

Dnew=Dold+ΔD(Pnew>Pold)

(16)

Dnew=Dold-ΔD(Pnew

(17)

式中:ΔD即为扰动步长;ΔD的取值对整个追踪过程至关重要,ΔD过大，收敛速度快，但是精度低，反之，ΔD过小，收敛速度慢，但是精度高。

2.3 灰狼算法和扰动观察法与MPPT协同控制

由于灰狼算法的收敛因子是呈线性变化的，因此其收敛的速度和搜索的精度负相关，为了缓解这种矛盾，本文将扰动观察法与其结合，最大程度兼顾二者的优点。

将该方法应用于PSC下的MPPT控制，狼的位置是实现最大功率跟踪控制的Boost电路的占空比，从而消除了PI控制回路。这使得控制器的设计和运算更加简化。

若狼群数目过多，会增加搜索的时间，过少会影响搜索精度，考虑狼群数目设为10，通过运行基于灰狼算法的MPPT，发现在迭代次数达到5时即可到达最大功率点附近，因此考虑将最大迭代次数设为5。算法流程见图3。

图 3 GWO-P&O算法流程图

由图3所示的算法流程图可以看出，该算法在MPPT应用的具体步骤为：

1)GWO 初 始化 10只狼的位置。在0.1-1的占空比范围内等距分布，狼的位置即占空比。

2)以光伏阵列的输出功率P作为适应度函数来评价狼的等级，保留适应度最好的三只狼，引导其他狼向该三只狼的位置靠近。

3)依据公式(9)—(15)更新灰狼位置，向最大功率点靠近。

4)当达到最大迭代次数和锁定最大功率点附近位置时，采用小步长的扰动观察法进行局部搜索，直至找到精确的最大功率点位置。

3 仿真验证及结果分析

为了验证上述算法的合理性和有效性，在Matlab/Simulink中搭建了完整的光伏阵列MPPT系统模型(图4)。主要由5×2的光伏阵列，MPPT控制器，Boost电路，阻性负载构成。

图 4 MPPT系统结构图

其中，单个光伏板的最大功率为213.15 W，短路电流7.84 A，开路电压36.3 V。Boost电路的参数为：Cpv=500 μF、C=20.25 μF、L=8.5 mH。电阻负载R=20 Ω。开关频率为20 kHz。

分别采用GWO 、P&O和GWO-P&O 算法，按照仿真表1中STC(均匀光照条件下)和PSC2(局部阴影条件下)两种不同的工况进行MPPT 系统仿真，分析比较各算法的收敛速度和追踪精确度。仿真结果见图5、6。由图5可知，在均匀光照条件下，三种算法均能实现最大功率点跟踪。其中灰狼算法(GWO)在0.8 s后进入稳定状态，收敛速度最慢，振荡幅度偏大。扰动观察法(P&O)经过0.1 s达到最大功率点，振荡较小。而GWO-P&O算法在0.5 s左右跟踪到最大功率2129 W并进入稳定状态下，振荡幅度不超过1 W，协同控制效果极佳。

(a)GWO算法

(b)P&O算法

(c)GWO-P&O算法图 5 STC条件下三种不同算法的MPPT仿真波形

(a)GWO算法

(b)P&O算法

(c)GWO-P&O算法图 6 PSC2条件下三种不同算法的MPPT仿真波形

由图6可知，当处于局部阴影状态下时，只有灰狼算法和GWO-P&O算法满足了MPPT寻优要求，扰动观察法陷入局部最优解，最后稳定于1204 W附近。灰狼算法在0.8 s时完成寻优任务，实际追踪功率1424 W， 振荡较大。

GWO-P&O算法依然可以在0.52 s左右精准定位到最大功率1440 W，几乎没有振荡。三种算法的具体性能比较见表2。

由仿真结果和表2的具体性能参数可知。基于GWO-P&O算法的MPPT无论是在均匀光照还是局部阴影条件下，都可以准确地实现最大功率跟踪。相比于其他算法，复合算法兼顾了速度性和精确性。与扰动观察法相比，复合算法成功实现了最大功率点追踪，没有陷入局部最优解，追踪效率提高了16.39%。与灰狼算法相比，追踪效率提高了1.11%，收敛速度提高了35%。除此之外，复合算法的振荡幅度非常小，大大减少了功率损失，非常适合于工作在局部阴影场景下。

表2 基于不同算法的MPPT控制性能比较

4 结论

针对局部阴影条件下的MPPT控制面临的问题，提出了一种基于灰狼算法和扰动观察法协调控制的MPPT控制策略。仿真软件验证了局部阴影下光伏阵列输出功率的多峰值特性。基于Matlab/Simulink建立了不同局部阴影条件下的MPPT系统仿真模型，检验了所提出的GWO-P&O算法的有效性。与其他MPPT算法的比较表明，本文提出的基于GWO-P&O复合控制的MPPT算法在提高跟踪效率的基础上，具有更快的跟踪速度，同时减少了因功率振荡造成的功率损失。