源于模型，变式拓展，实现教学价值最大化——对一类含45°角几何问题的探究实践

■朱建良

罗增儒教授说过，数学解题有四步：记忆模仿、变式练习、自发领悟、自觉分析。其中，自发领悟层次的要求较高，它是对解题内蕴的深层结构进行剖析，是从感性层面到理性层面来认识问题的本质特征。而在数学课堂教学中，将系列变式问题与课堂生成的问题进行整合，巧妙穿插，能使学生达到较好的融会贯通、自发领悟的学习效果。

下面是对一类含45°角几何问题的探究实践，从模型出发，通过挖掘教材、一题多解、变式拓展，彰显解题方法蕴藏的数学思想以及每个环节蕴含的数学思维价值，以期提高学生的思辨推理能力，实现教学价值的最大化。

一、品味模型，睿智追问

模型呈现：如图1，在正方形ABCD中，点E、F分别在AB、BC边上，AB=9，FC=2BF，CE、AF交于点G，且∠AGE=45°，求CE的长。

图1

对问题进行多样化探究可以概括事物的数量关系和变化规律，教给学生获取知识的方法，激发学生的思维。探究这类正方形背景下的含45°角的几何问题时，教师可以适时引导学生进行联想、分析，在类比中思考，避免思维定式。

师：正方形是个完美的特殊图形，由题意可联想到正方形的“半角模型”。如图2所示，在正方形ABCD中，∠FAM=45°，延长CB至点N，使BN=DM，则有结论FM=BF+DM。那么，图1与“半角模型”有什么关系呢？

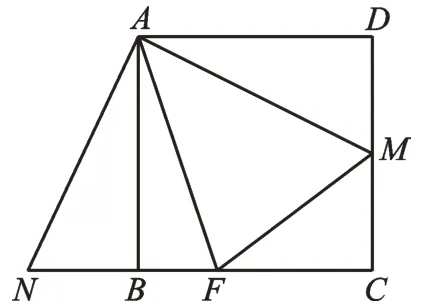
图2

生1：在图1中可以构造“半角模型”。过点A作EC的平行线，交CD于点M，连接FM，延长CB至点N，使BN=DM，利用“半角模型”以及勾股定理，可求出CE（图略）。

师：很好，学会联想模型，便水到渠成。能否另辟蹊径，建构直角三角形求解呢？

生2：可以，过点C作AF延长线的垂线，并过点F作CE的垂线，利用线段比例可求出CE。

师：如果在图1中连接AC，能证明吗？

图3

生3：可以。如图3，过点F作FH⊥AC于点H。∠1+∠2=∠3+∠4=∠2+∠3=45°，∴∠1=∠3，∠2=∠4，∴tan∠1=tan∠3=，FC=6，FH=HC=，AH，∴tan∠2=tan∠4=，∴BE=，∴EC=。

师（追问）：生3的研究框架是如何构建的？顺势再研究，还有不同的求解方法吗？

生4：有。如图4，连接AC，过点E作EH⊥AC于点H，tan∠1=tan∠3=（生3的解法）。设EH=x，则HC=3x，AC=4x=，∴x=，∴CE=。

图4

师：很精彩，连老师都没有发现这种方法。如图5，过点A作AM∥EC交DC于点M，大家观察图形，可发现什么结论？

图5

生5：有tan∠DAM=tan∠ECB，还有平行四边形AECM，求出MC，就能得到EC。

此时，有学生提出，也可通过证明Rt△ADM≌Rt△CBE或过点A作CE延长线的垂线来解决问题。生3构造直角三角形，将角自然转化为锐角三角函数，由特殊位置建立边的数量关系，为学生进行深度思考添加了催化剂，引爆了学生的思路，令人意外又合情合理，突显了数学思维，真正体现了“知识与技能”的学习目标。

师：我们要学会观察，学会转化，把不熟悉的问题转化为熟悉的问题。这个案例隐藏了丰富的内涵，这几位同学的解法背后蕴藏了什么样的数学观点或数学思想？

通过解法剖析，挖掘正方形中45°角问题的横向联系，体现了基础知识的联系性；由基本的模型出发，添加辅助线，变换图形位置，发展了学生的多向思维方式；由数到形，对几何题的条件进行变式，对问题进行深度探究，既体现了研究问题的方法多样性，又体现了数学推理的严谨性，逐步完善了学生的知识结构，培养了学生举一反三的数学学习能力。

二、变式模型，意义建构

变式：如图6，在△ABC中，∠C=90°，点F在BC上，且BF=AC。点E在AC上，且AE=CF，AF与BE相交于点P，求证：∠BPF=45°。

图6

师：请大家思考，如何在Rt△ABC中构造数学模型？

生6：如图7过点B作BC的垂线，取BD=FC，连接DF、AD，即可证明。

图7

生7：过点F作BC的垂线，取FD=FC，连接BD、DE，利用全等三角形（图略），也能证明。

设计意图：对原模型做变换，把问题情境放置在三角形中，延续了对之前问题的研究，化未知为已知，发散了学生的思维，培养了学生的数学抽象、逻辑推理、数学运算等核心素养。

三、深化问题，一般化结论

拓展：如图8，梯形OABC，OA∥BC，OA=4，OC=，BC=1，AB=，∠COD=45°，求AD。

图8

师：问题情境变化为梯形中的45°角问题，与变式问题的图形相比，你有什么发现？

生8类比生6的解法，延长线段OC、AB至相交，由构造三角形全等转化为构造三角形相似来解决问题

师（追问）：大家看看从形的角度能否寻找到思路。如果连接OB，有相似三角形吗？

生9：有，△BCO∽△ADO，再算出BO，由线段之比即可得到AD。

构造相似三角形，构图简洁，计算量小，这些解法自然也是一种更优化的解法。本拓展突出了问题变式中图形本质属性的一致性，引导学生进一步理解基本图形关键属性的变化，加深学生对图形相似的理解。

生10：如图9，延长线段AO至F，使OF=1，连接CF，过点C作CE⊥AF于点E。构造等腰直角三角形CEF，∴∠CFO=45°，∴∠COD=∠CFO=45°，∴∠FCO=∠DOA。

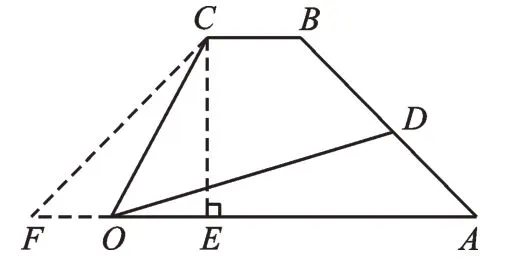
图9

师：为什么截取OF=1？构造Rt△CEF有类似方法吗？为什么要构造Rt△CEF？

生11：连接OB，△OBA为等腰直角三角形，截取OF=BC=1，可构造出等腰Rt△CFE。

生12：也可直接作∠CFE=45°。

生13：证明△COF∽△ODA，然后求出AD。

学生思维活跃，研究氛围浓郁。设计系列变式问题，不断变换知识的非本质特性，让新知识和学生已有的经验建立有意义的关联；合理转化梯形中的45°角问题，在拓展变化的过程中突出知识的关键属性，展现数学知识间的纵横联系，构造相似三角形或直角三角形，展现知识的发生和发展过程，有助于学生掌握一般化的方法。

至此，探究完成。在教学中，教师如果尝试由基本图形出发，变式拓展问题，一题多解，一题多变，类比探究，不仅能够激发学生学习数学的兴趣，还能丰富解题方法，使学生举一反三，触类旁通，认清问题本质，深化对问题本质的理解，收到事半功倍的效果，有效提升学生的学科素养。