基于正交试验的坑中坑加固效果影响因素分析
2022-05-06朱亚林李勇海汪亦显
檀 昆, 朱亚林,2, 李勇海, 汪亦显,2, 洪 胤
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.土木工程结构与材料安徽省重点实验室,安徽 合肥 230009; 3.中铁四局集团 第二工程有限公司,江苏 苏州 215131)
0 引 言
随着城市的发展建设,地下空间的开发利用逐渐增多,地下基坑工程也向着更深更宽更复杂的方向发展。为满足某些基坑工程中地下室、电梯井及部分基础结构建设的需要,往往需要进行二次开挖,形成坑中坑。目前相关规范中缺少关于坑中坑的介绍及其计算方法的内容,导致在坑中坑围护结构设计时常常因忽视坑中坑的影响而带来风险,或是过度考虑坑中坑的存在而造成资源的浪费[1]。另外,坑中坑一般处于第2层、第3层土中,土质较差,尤其是在软土地区,土体抗剪强度较低,压缩性大,常规的围护结构很难完全发挥其控制变形的作用,因此技术人员考虑利用土体加固的方式改善土体力学性质,事实证明,对基坑土体进行加固可以较好地降低基坑变形、提升基坑稳定性[2-3]。
目前对坑中坑问题和基坑土体加固问题的研究已有一些成果。文献[4-5]通过建立有限元模型,分别研究几个表现坑中坑特点的参数对基坑应力场和对围护结构变形的影响;文献[6]基于实际工程项目和离心试验,总结内外坑间距对地连墙位移影响的变化趋势;文献[7]通过数值模拟计算推导出坑中坑等效深度的计算公式,并与其他方法相比较验证公式的正确性;文献[8-10]从理论方面对围护结构内力计算方法进行改进,提出适合于坑中坑围护结构的土压力计算方法;文献[11-12]从基坑加固对周边环境的影响考虑,探究不同加固范围及加固程度对邻近桩身变形的影响;文献[13-14]提出加固体深度、宽度存在临界值,超出该值后继续提升加固尺寸带来的加固效果不明显;文献[15]建立基坑地面沉降、坑底隆起及围护桩侧向位移这些性状与加固体刚度的关系曲线,并进行拟合得到相应关系式,具有一定参考价值。
目前对于坑内加固的相关研究,大多针对加固体对普通基坑的影响,而对坑中坑的土体加固研究很少。本文利用MIDAS/GTS有限元软件建立二维坑中坑模型,研究坑中坑加固的最佳区域,提出最合适的加固尺寸,并通过改变加固体在平台中的位置以及加固体弹性模量2个关键因素来探究其对加固效果的影响,最后设计正交试验,利用极差分析法和方差分析法对加固体深度、加固体宽度、加固体弹性模量及加固体在平台中的位置这4个影响加固效果的关键因素的敏感性进行排序,以期为实际坑中坑工程设计和施工提供一定的理论指导。
1 有限元模型的建立
1.1 几何模型
在某些坑中坑工程中,为满足地下室的活动空间,基坑的内坑开挖尺寸往往较大,因此本文计算模型将坑中坑外坑深度设为6 m,内坑深度取5 m,坑中坑平台宽度为10 m,内坑宽度取40 m;另外,考虑基坑开挖的影响范围,将模型总宽度设为160 m,总深度设为60 m;鉴于基坑模型左右对称,取模型1/2进行计算分析。本文模型中内、外坑开挖深度不深,且上部土质较软,需考虑对土体进行加固,因此计算模型采取排桩+加固体的支护方案,后续的计算结果表明该方案是可行的。在排桩设置方面,外坑和内坑分别采用直径1 200、1 000 mm的钻孔灌注桩,桩间距均设置为1 m;外坑灌注桩桩长为15 m,插入深度9 m;内坑灌注桩桩长12 m,插入深度7 m。
模型建立时,土体采用MIDAS中位于同一平面上的3、4个节点定义的三角形或四边形单元——平面应变单元模拟,灌注桩利用结构单元中2个节点定义的线单元——梁单元模拟,对模型左、右两侧分别设置X方向的位移约束,在模型底部设置X、Y方向的位移约束[16]。坑中坑有限元计算模型如图1所示。
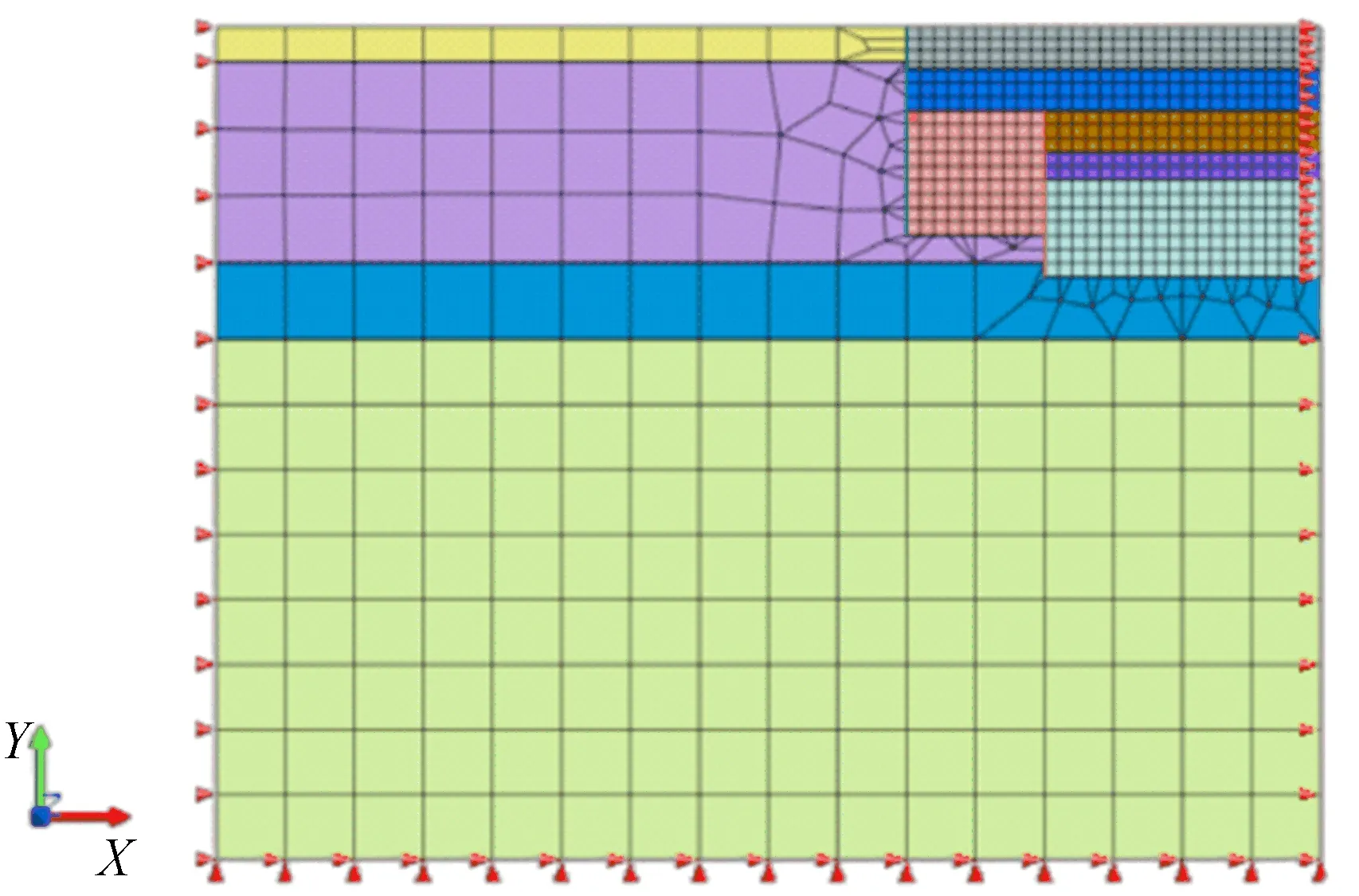
图1 坑中坑有限元计算模型
1.2 材料参数
计算模型中,土体及加固体选用Mohr-Coulomb强度准则[17];围护桩材料为混凝土,可用弹性模型进行计算分析。
坑中坑采用水泥土搅拌桩加固方式,有关实验表明[18]经水泥土搅拌加固后的土体黏聚力和内摩擦角分别为天然土体的10~20倍和2倍左右。本文加固体黏聚力取天然土15倍,为450 kPa;内摩擦角取2倍,为26°。
文献[13]提到,水泥土的弹性模量一般为水泥土无侧限抗压强度的100~120倍,而后者与水泥掺合比和养护龄期相关,本文加固体水泥掺合比取15%,养护龄期为28 d,查表[19]可得水泥土无侧限抗压强度为1.35 MPa,若弹性模量与抗压强度关系选为110倍,则可取加固体的弹性模量为150 MPa。
材料物理、力学性能参数见表1所列。
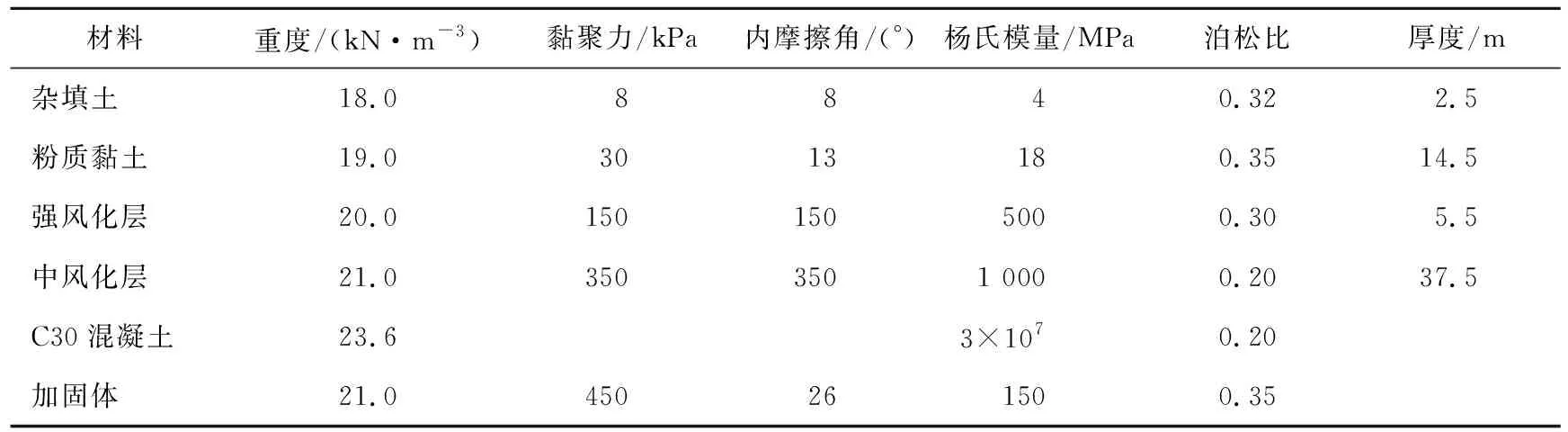
表1 材料物理力学性能参数取值
2 计算结果与分析
计算时将坑中坑施工分为6步,即施作外坑围护桩、开挖至外坑3 m深处、开挖至外坑底、施作内坑围护桩、开挖至内坑3 m深处及开挖至内坑坑底,内、外坑围护桩在开挖至内坑坑底工况下处于最不利状态,故对该工况下内、外坑围护桩的侧向位移进行分析,研究加固体位置、尺寸及加固程度对内、外坑围护桩侧向变形的影响。
2.1 加固最佳位置的确定
目前对于坑中坑的加固位置,往往都是依靠经验将加固体设置在坑中坑平台靠近外坑围护桩一侧。下面将加固体分别设置在外坑主动区、平台靠外坑围护桩一侧、平台靠内坑围护桩一侧以及内坑被动区4个区域,以研究坑中坑加固体的最佳加固位置。加固体4种加固位置类型如图2所示。图2中:H为加固体深度,即外坑开挖深度;B为加固体宽度,即坑中坑平台宽度。
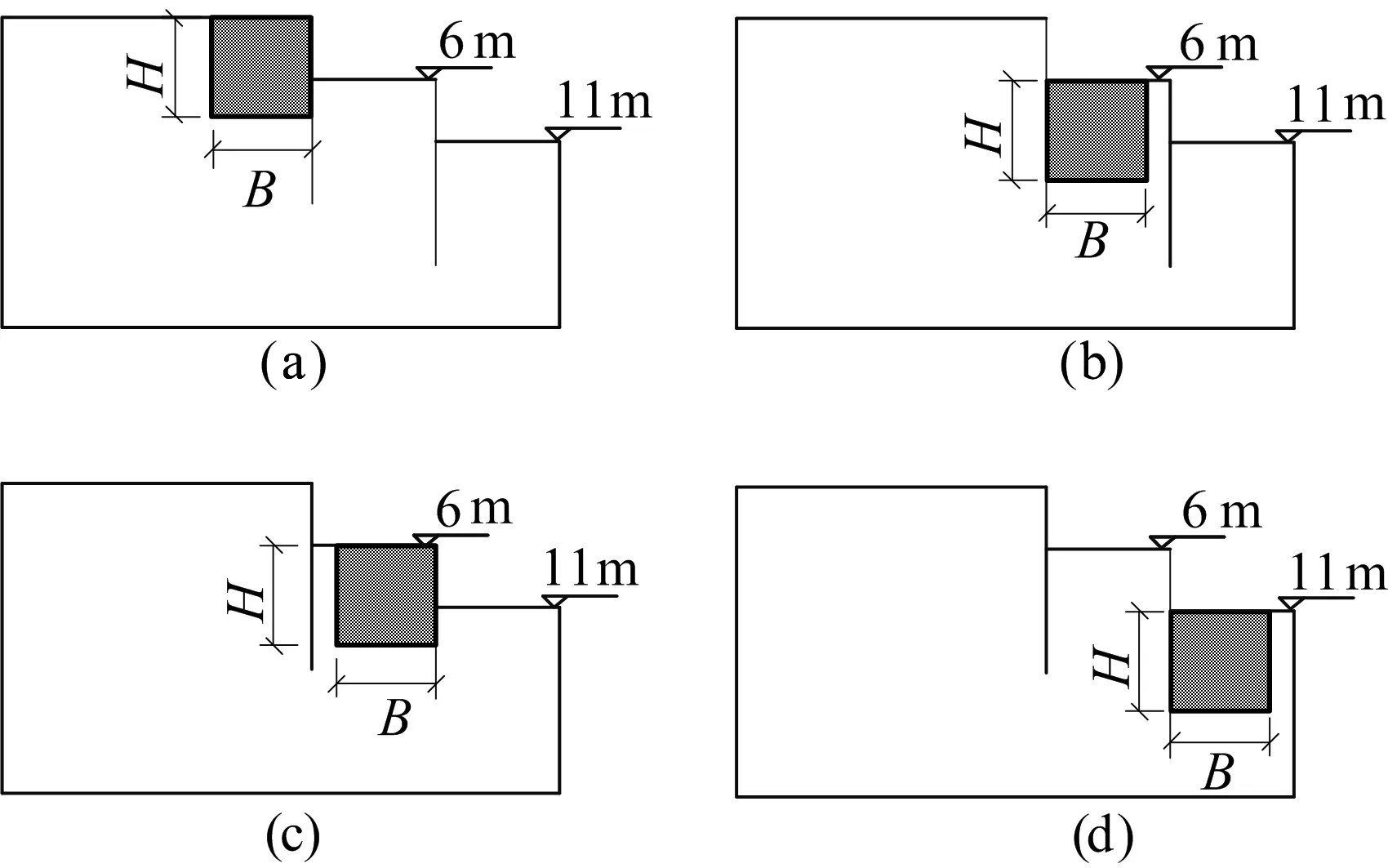
图2 加固体4种加固位置类型
通过建立以上4种加固位置模型,并将每个模型的加固体尺寸按1×1至8×8逐步变化,得出4种加固位置上各64个不同加固尺寸下外坑、内坑围护桩的位移表现。本文提取各种情况下内、外坑围护桩桩身最大侧向位移值,并将这些位移值按加固位置分类,分别找到最佳加固尺寸(即使得位移最小时的加固尺寸)下的桩身位移最大值进行比较分析,具体位移情况见表2所列。
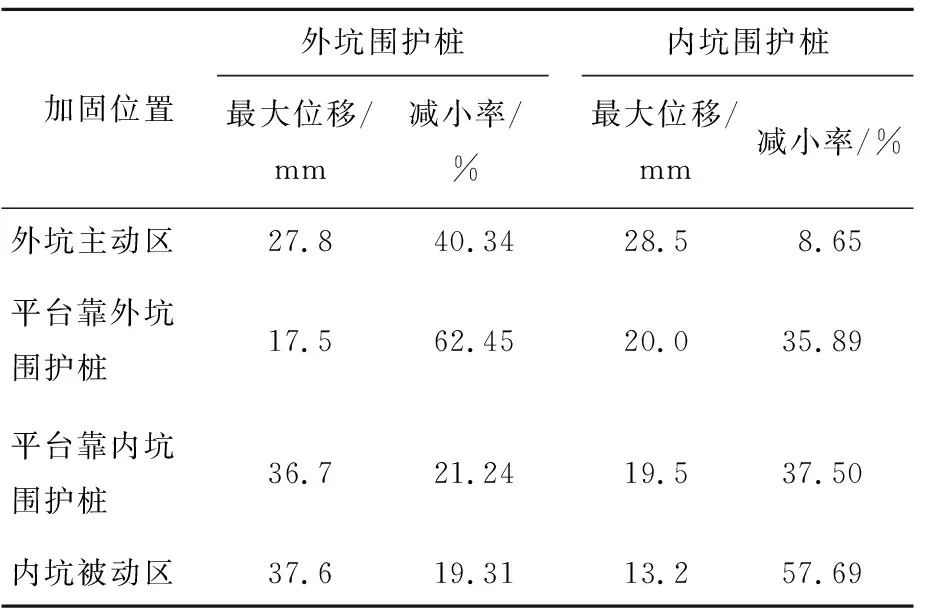
表2 不同加固位置下的围护结构侧向位移
从表2可以看出,在一定的加固尺寸下内、外坑围护桩的侧向位移均相较于未加固情况下有所降低,可以证实坑中坑加固对基坑围护结构有利。将各情况下围护桩侧向位移最大值与未加固时的围护桩位移最大值进行比较,得出相应的位移减小率。从外坑围护桩看,对平台靠外坑围护桩的区域进行加固时,在最佳加固尺寸下位移减小率为62.45%,远超其他3种情况;对外坑主动区进行加固,位移减小率达到40.34%,可见对基坑主动区加固也能起到一定的效果;其他2种情况下,由于加固体离外坑围护桩较远,加固效果稍差。从内坑围护桩看,对内坑的被动区进行加固是最好的选择,在最佳加固尺寸时,位移减小率为57.69%;对平台靠内坑围护桩区域加固,即对内坑主动区进行加固时,加固效果也较好,减小率为37.50%,对比上述2种加固效果可知,对基坑被动区加固效果会略优于对主动区加固;值得一提的是,对平台靠外坑围护桩区域加固时,内坑围护桩位移减少35.89%,与对内坑主动区加固效果相差很小。
综上所述,在最佳加固尺寸下,对坑中坑平台靠近外坑围护桩一侧区域进行加固时,坑中坑内外坑围护桩侧向位移均有明显减小,而其他3种情况均无法在有效降低内坑围护桩位移的同时对外坑围护桩位移也有很好的控制效果。因此对于与该计算模型类似的坑中坑工程而言,对平台靠外坑围护桩区域加固是最佳的加固位置。
2.2 加固最合适尺寸的确定
在确定最佳加固位置后,对该区域进行不同尺寸的加固,令加固体深度在H/6~3H/2范围内变化,宽度在B/10~B范围内变化,以探究最合适的加固尺寸。不同加固尺寸下外坑、内坑围护桩最大侧向位移如图3所示。
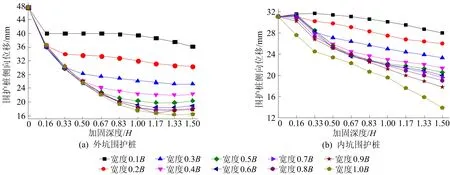
图3 不同加固尺寸下外坑和内坑围护桩最大侧向位移
从图3a可以看出:在加固宽度较小时,提升加固宽度会有效减少围护桩的侧向位移,但随着加固宽度增大至7B/10时,进一步增加加固宽度对加固效果的提升可以忽略不计;在每个加固宽度下都存在一个界限加固深度,且这个深度也随加固宽度的增加而相应提高;当加固宽度为7B/10时,这个界限加固深度为H,进一步扩大加固尺寸对外坑围护桩侧向位移的控制作用不明显,可确定该尺寸为外坑最适合加固尺寸。
从图3b可以看出:当加固宽度在9B/10以下时,超出B/2后,曲线十分接近,继续提升宽度意义不大,但随着加固体宽度达到B,即布满整个平台时,围护桩位移又产生进一步的位移,且幅度较大;加固深度的增加对加固效果的提升也很明显,当加固深度为3H/2时各加固宽度下内坑围护桩位移均达到最小值。综上所述,可以得出内坑围护桩最适合加固深度为3H/2,加固宽度为B。
由于分析得出的针对内、外坑围护桩的最合适加固尺寸不同,需要进行适当协调。计算出内、外坑围护桩位移最大值在各加固尺寸下相比于未加固时的减小幅度,得出对于内、外坑围护桩而言,减小幅度分别达到30%、60%后继续增加加固尺寸效果不明显。当加固深度为7H/6、宽度为3B/5时,内、外坑围护桩位移减小幅度首次分别达到30.9%、61.1%,不仅可以较好控制内、外坑围护桩位移,还可保证加固的经济效益。值得一提的是,加固尺寸设为外坑最适合加固尺寸时,内、外坑桩身位移最大值降幅分别为29.3%、61.1%,在相同的每延米加固面积下,其对内坑的加固效果较差;加固尺寸设为内坑最适合加固尺寸时,位移降幅则分别为55.3%、65.3%,但此时加固尺寸过大,经济性较差。综合考虑内、外坑围护桩的位移控制效果及经济性,加固深度为7H/6、宽度为3B/5是加固体最适合尺寸。
2.3 加固体距外坑距离对加固效果的影响
加固体选用最适合加固尺寸,考虑加固体左端距外坑围护桩分别为0、1、2、3、4 m共5种情况,内、外坑围护桩位移计算结果如图4所示。
从图4a可以看出:当加固体紧贴外坑围护桩时,围护桩侧向位移沿桩身分布比较平均,最大值出现在桩顶,为18.5 mm;当加固体逐渐远离外坑围护桩后,外坑围护桩侧向位移沿桩身分布呈上大下小的趋势,桩身高度4 m以下部位的侧向位移值随距离增长而逐渐减小,4 m以上部位则随之增大;当距离为0、1 m时桩顶侧向位移分别为18.5、33.1 mm,变化幅度较大,为78.9%,1~2 m、2~3 m、3~4 m内的增长幅度分别为19.6%、3.5%、0.9%,可见随着加固体逐渐远离外坑围护桩,桩身位移变化的幅度会逐渐减小。
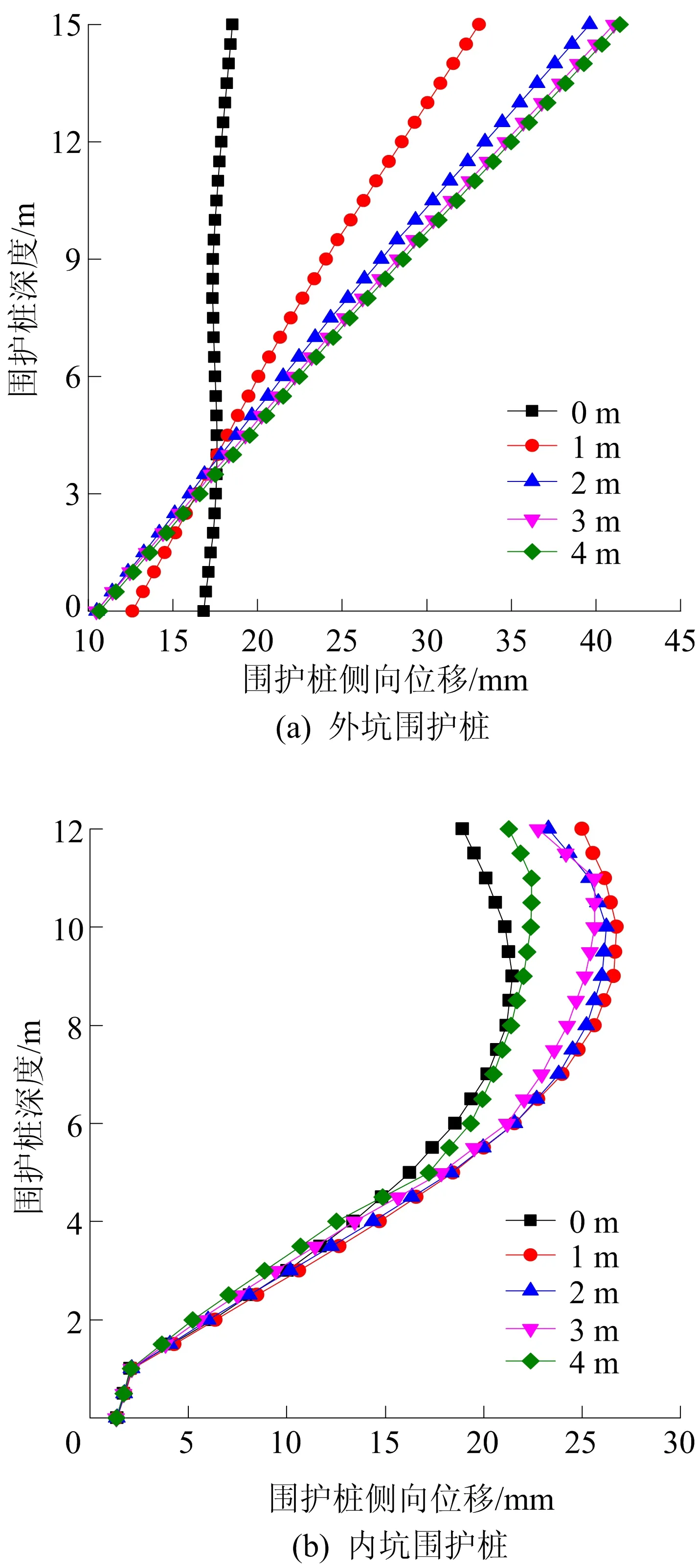
图4 不同距离下外坑、内坑围护桩侧向位移变化曲线
从图4b可以看出:在不同的位置处,内坑围护桩桩身位移趋势是类似的,均表现出中间大两边小的情况,且加固体位置的改变对内坑围护桩桩身上半部分影响较大,而对下半部分基本无影响;当加固体紧贴外坑围护桩时,内坑围护桩桩身上部侧向位移最小;当加固体距离外坑围护桩为1 m时,内坑围护桩位移最大,桩身位移最大值为26.7 mm,此后进一步增大距离,内坑围护桩桩身各位置处的位移均有一定程度的减小,当加固体紧贴内坑围护桩时,内坑围护桩位移与紧贴外坑围护桩时接近,但桩顶位移还有6 mm左右的差距。因此,在实际工程中应注意加固时将加固体紧贴外坑围护桩,以达到最佳的加固效果。
2.4 加固体弹性模量对加固效果的影响
当水泥掺入比过小时,不能产生加固效果,掺入比过大时,经济性较差,水泥土会趋于脆性破坏,因此在一般地基加固工程中,水泥掺入比在7%~20%是合适的,通过查表并结合文献[20]提出的经验公式可以推导出对应弹性模量的范围在35.5~427.2 MPa之间。本文对该范围进行适当调整,使其在40~400 MPa范围内变化;选用最合适加固尺寸,并将加固体设置在平台紧贴外坑围护桩一侧,以控制其他变量的影响。不同弹性模量下外坑、内坑围护桩侧向位移曲线如图5所示。
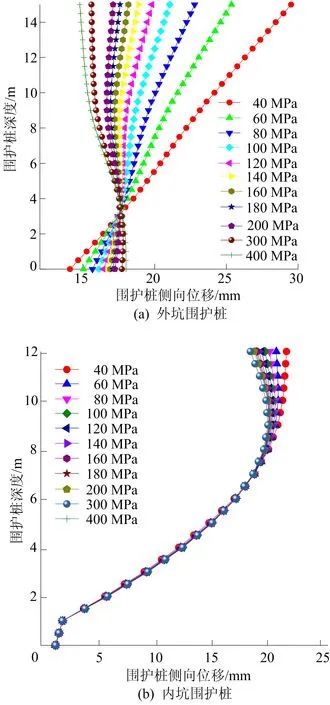
图5 不同弹性模量下外坑、内坑围护桩侧向位移变化曲线
从图5可以看出:当弹性模量从40 MPa增加到400 MPa时,外坑围护桩桩顶位移从29.5 mm减小至14.8 mm,减小幅度为49.8%;内坑围护桩桩顶位移从21.3 mm减小至19.2 mm,幅度为9.8%,可见加固体弹性模量的改变对外坑围护桩的影响更大。由图5a可知:随着加固体弹性模量逐渐增大,围护桩桩身3 m以上部分的位移逐渐减小,而3 m以下部分的位移逐渐增加;加固体弹性模量在120 MPa以下时,提高加固体弹性模量,加固效果有显著提高;超出120 MPa后,进一步提高加固体弹性模量对围护桩位移的控制效果不明显。由图5b可知,加固体弹性模量的影响不大,尤其是在桩身8 m左右以下的部分,基本不会随着加固体弹性模量的增大而发生变化,而桩身8 m以上的部分仅在60 MPa以下时有所影响,且影响程度较小。
3 加固效果影响因素的正交分析
本研究中,影响加固效果的因素为加固体深度、加固体宽度、加固体距外坑距离及加固体弹性模量。在确定影响坑中坑加固效果的4个因素后,有必要对这些因素进行相应的敏感性程度和显著性分析,从而重视最敏感因素,以最经济的方式充分发挥加固体的加固效果。上述4种因素相互组合会产生不同的加固效果,若每个因素取4个水平,采用交叉组合方法,则共有44即256种试验方法,工作量很大。本文利用正交试验方法,在保证各试验因素均衡搭配的同时大大降低试验次数[21],提高工作效率。
3.1 正交试验表的建立及试验结果
分别将加固体深度、加固体宽度、加固体弹性模量和加固体距外坑距离设为因素A、因素B、因素C、因素D。试验因素及水平取值见表3所列,各水平等间距变化,且保证各水平选取均在合适范围内。
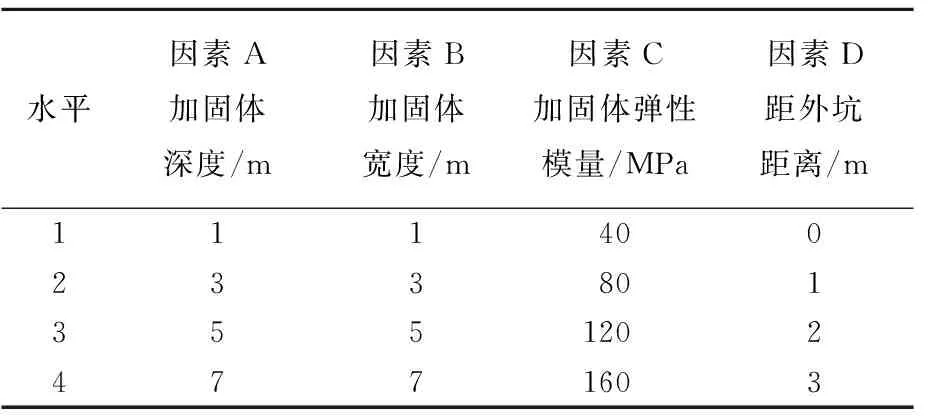
表3 试验因素水平取值
综合考虑试验因素和水平数,本文采用L16(45)正交表,即做16次试验,包含5个因素,每个因素有4个水平。因为本次研究涉及的因素仅4个,所以第5个因素所处列为空列,可作为误差分析列参与试验。正交表设计完成后,需保证在表中每列不同数字出现的次数相同,任意2列中同行相邻2个数组成的有序数对出现的次数也相同,以满足正交表“分散均匀,齐整可比”的要求[22]。对设计完成的16组正交试验进行计算,取各试验中内、外坑围护桩侧向位移最大值作为试验结果,并计算不同因素、不同水平情况下各试验结果的均值。正交试验表及试验结果见表4所列。
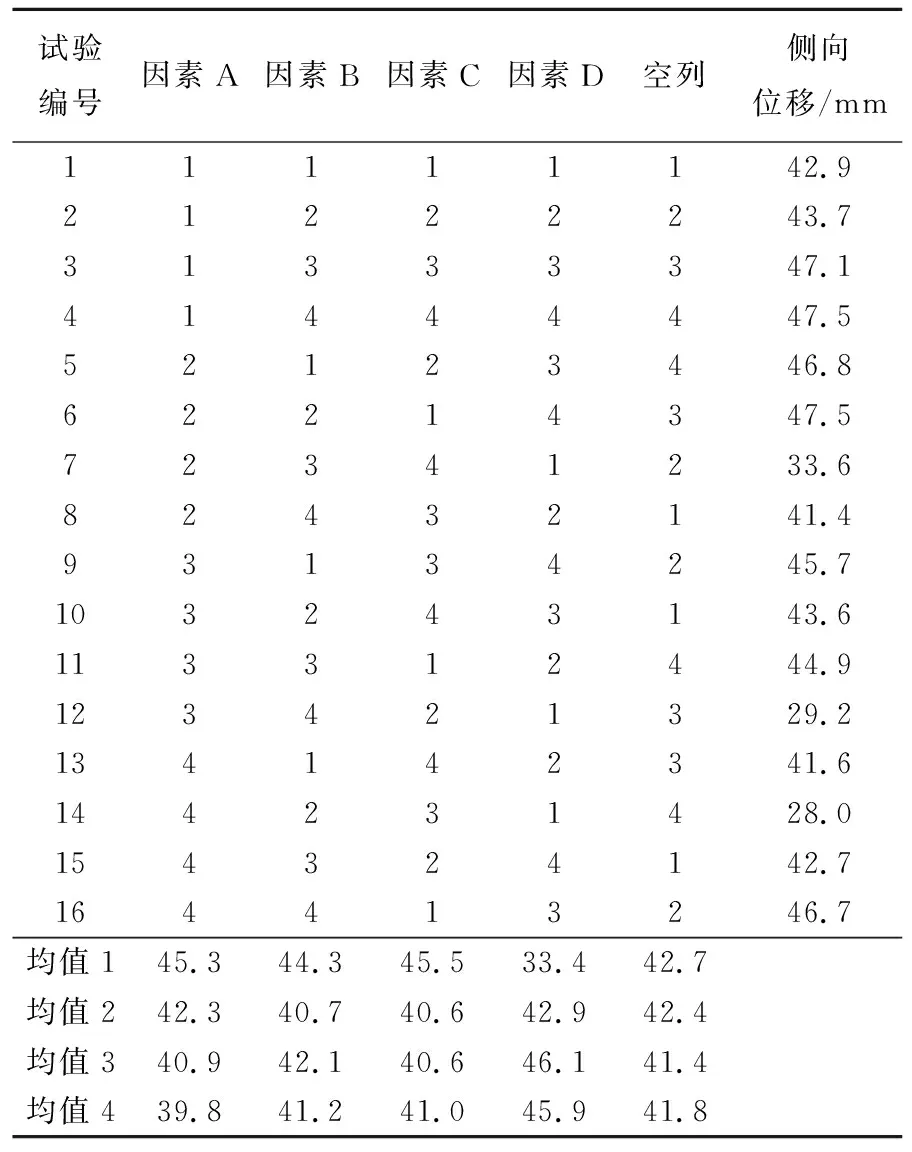
表4 正交试验表及试验结果
3.2 极差分析
极差分析法是对正交试验结果分析的最常见方法,通过对比各因素在各水平下试验结果平均值的最大值和最小值之差来判断因素的敏感性大小,这种分析方法仅需对试验结果进行少量计算便可得出最佳加固方式和最敏感因素。正交试验极差分析结果见表5所列。表5中:δ为各因素在各水平下的试验结果平均值与所有试验总均值之差;T为各因素下δ最大值与最小值之差。
由表5可知,各因素按敏感性从大到小依次为加固体距外坑距离、加固体深度、加固体弹性模量、加固体宽度,这表明加固体在平台中所处的位置对加固效果的影响是最大的,而加固体宽度的影响程度最小。另外,由δ值可以得出,在已有水平情况下,选用A4B2C3D1组合可以最大程度降低内、外坑围护桩侧向位移最大值,是最优的组合方案。

表5 正交试验极差分析结果 单位:mm
3.3 方差分析
极差分析法由于其计算简单、直观明了的特点被广泛用于正交分析中,然而这种方法也存在一定的缺陷,其无法区分不同的试验结果是由因素水平改变而产生的,还是由试验误差而产生的[23],而方差分析可以弥补极差分析在这方面的不足,并对因素影响的显著性作出定量评价,保证分析的精确性。
正交试验方差分析结果见表6所列。表6中:各因素偏差平方和S=m∑(xi-μ)2,m为各因素的水平数,xi为各试验结果,μ为所有试验结果的均值;自由度f=m-1;均方为偏差平方和与自由度的比值;F比为各因素的均方与误差均方的比值。
方差分析中引用F分布临界值表来进行各因素的显著性水平分析,在确定因素自由度与误差自由度均为3后,在分布临界值表中查找相应可靠度条件下的F分布临界值,其中F0.01(3,3)、F0.05(3,3)、F0.1(3,3)分别表示可靠度为99%、95%、90%时的分布临界值,将计算出的各因素F比与临界值对比,判断各因素的显著性情况。若F比在F0.1(3,3)~F0.05(3,3)范围内,则说明该因素的影响不显著;若F比在F0.05(3,3)~F0.01(3,3)范围内,则说明该因素的影响显著;若F比大于F0.01(3,3),则说明该因素的影响非常显著。
从表6可以看出,4个因素的F比均大于F0.1(3,3),可知各因素对加固效果均有一定程度的影响。按F比大小排序,可知加固体距外坑围护桩距离对加固效果影响最大,其F比远高于其他3个,且是值唯一大于F0.01(3,3)的因素;加固体深度的影响次之,故在确定加固体位置后可以首先考虑在合适范围内增加加固体深度,这样对加固效果的提升最大;加固体弹性模量的显著性大小次于加固体深度,但两者相差不大,可以看出在适当范围内提高加固体弹性模量也是有效的加固措施;加固体宽度对加固效果的影响最小,也是唯一被评价为不显著的因素,因此首先考虑增加加固体宽度来提升加固效果的做法是不可取的。
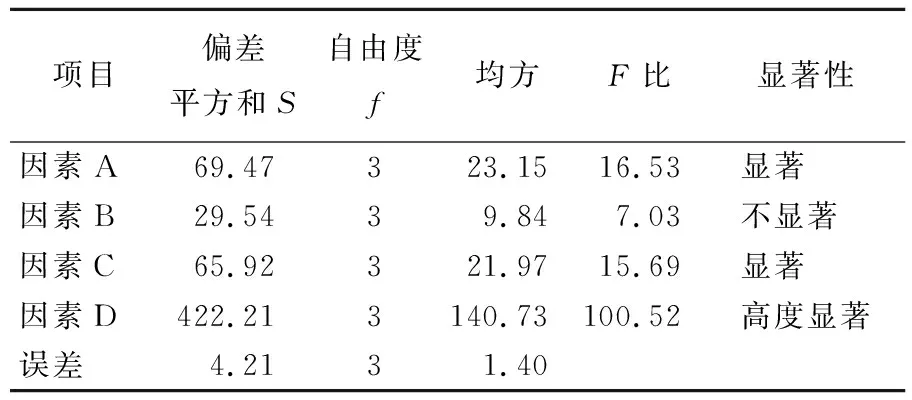
表6 正交试验方差分析结果
4 结 论
本文利用MIDAS/GTS有限元软件模拟坑中坑模型,研究坑中坑最佳加固区域,提出最合适加固尺寸,并通过改变加固体在平台中的位置及加固体弹性模量等关键因素来探究其对加固效果的影响,最后设计正交试验来确定关键因素的显著性,得出以下结论:
(1) 将加固体设置在平台处靠外坑围护桩一侧时,对外坑围护结构位移的加固效果远优于其他位置,对内坑围护结构位移的控制效果也能维持在较高水平,实际施工时应优先考虑将加固体设置在该区域。
(2) 在对平台靠外坑围护桩一侧加固时,加固深度和加固宽度都有一定的限值,超过该限值后进一步提升加固尺寸对加固效果的提升不大,综合考虑加固体对坑中坑内、外坑围护桩侧向位移的影响,得出加固体深度为7H/6、宽度为3B/5是最适合的加固尺寸。
(3) 加固体远离外坑围护桩后,外坑围护桩侧向位移增大主要体现在桩顶位置处,且进一步远离后外坑围护桩侧向位移增长幅度会逐渐减小;内坑围护桩侧向位移随加固体逐渐远离外坑围护桩呈先增后减的趋势,且变化主要体现在桩身上半部分。
(4) 改变加固体弹性模量对外坑围护桩的影响要远大于内坑围护桩,且加固体弹性模量对内、外坑围护桩侧向位移的控制作用有一定的限值,超出该限值后对加固效果的提升不大。
(5) 影响加固效果的4个因素中,加固体距外坑距离因素的影响是最显著的,其次分别为加固体深度、加固体弹性模量,最后为加固体宽度,且对于类似工程,由极差分析可估计在已有水平中A4B2C3D1为最优组合,加固效果最好。
