磁感应下Chay神经元的簇发与同步转迁

马娟娟，李新颖，杨宗凯，达虎

1.兰州交通大学数理学院，甘肃兰州730070；2.兰州交通大学电子与信息工程学院，甘肃兰州730070；3.甘肃省计算中心，甘肃兰州730046

前言

数以亿计的神经元组成的神经系统是庞大又复杂的信息网络。神经元间通过电突触和化学突触连接，使得神经系统具有复杂的非线性动力学现象。神经元模型通常都是多尺度模型，包括脉冲放电过程相关的快变量过程和静息态有关的慢变量过程，其中，由静息态转迁变化的慢变量对脉冲放电的慢变量有调节作用，这个过程形成了簇放电现象。

Rinzel 等［1］首次提出的快慢动力学分析是研究两时间尺度簇发动力学的重要方法，得出簇发的本质原因是系统在沉寂态和激发态间相互转换的结论。文献［2］用分岔理论研究了不同快慢动力学现象，认为不同的分岔类型会导致不同的快慢动力学现象。文献［3］对Chay神经元模型改进之后，对各种快慢动力学的产生机理以及不同放电行为转迁原因做了深入研究。文献［4］研究了一类改进的Morris-Lecar 神经元模型，发现由于系统中存在不同的分岔行为，产生两种不同的快慢动力学现象。

耦合神经系统的同步性研究是非线性科学研究的核心问题。耦合系统的同步转迁过程可以借助相似函数来量化研究。文献［5］研究了以化学突触耦合的Hindmash-Rose 神经元模型在耦合强度和拓扑结构的影响下系统同步性的转迁过程，使得读者对化学突触耦合神经元系统有了进一步深入的了解。文献［6］通过相位差和互相关函数判断两个电耦合且非恒等的Hindmash-Rose 神经元的同步，得到两个神经元耦合系统随着电耦合强度的增加，实现从簇同步到相位同步最终到达拟完全同步的过程。

在神经元系统中，化学突触相对于电突触更具有普遍性。化学突触可分为兴奋性化学突触和抑制性化学突触。文献［7］中对两个化学突触耦合的兴奋性神经元进行研究，结果表明兴奋性化学突触可以使神经元模型实现从峰放电到簇放电的转迁过程。次外，分析了抑制性化学突触耦合模型的动力学行为，且以上两种耦合方式都用相平面分析法揭示了簇的产生机制。文献［8］研究了在噪声作用下化学突触耦合Morris-Lecar 神经元的动力学行为。研究表明，由于化学突触的复杂性和多边性，其在优化噪声强度处增加的相关性比电突触耦合更有效，所以化学突触耦合神经元模型的动力学行为值得进一步研究。

通过上述研究，本文首先在Chay 神经元模型中加入电磁感应建立了四维微分方程模型，通过Matcant 数值仿真，得到以慢子系统状态变量为分岔参数，快子系统在不同参数范围下呈现出的簇发类型，并对其分岔过程做简要分析。其次通过C语言仿真，研究了Chay 神经元耦合系统在电磁效应和化学突触耦合共同作用下神经元耦合系统的同步转迁过程。

1 模型描述

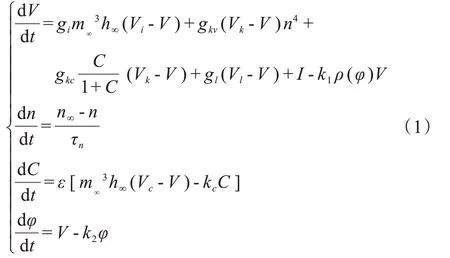
其中，dV/dt表示膜电位V的变化；dn/dt表示依赖于位的K 离子通道打开概率的变化规律；dC/dt表示细胞膜内Ca 离子浓度的变化规律；dφ/dt表示膜电位与电磁效应的关系。其中ρ(φ) =α+ 3βφ2是神经元的电磁效应；Vk、Vi和Vl分别是K 离子通道、混合Na 离子-Ca 离子通道和漏电离子通道的可逆电位；gi、gkv、gkc、gl分别代表各通道的最大电阻。kc是细胞膜内Ca 离子流出的比率常数，ε是比例性常数，Vc是Ca 离子通道的可逆电位，k1、k2为感应参数增益反馈系数。

方程中m∞和h∞分别是混合Na 离子-Ca 离子通道激活和失活概率的稳态值，n∞是K 离子通道打开概率n的稳态值，其具体表达式为：

其中：

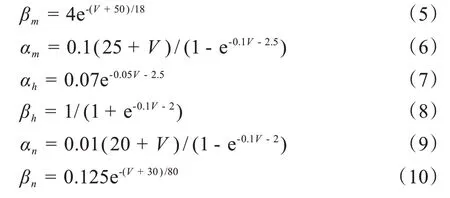
门控电位K离子通道的弛豫时间τn遵循如下方程：

其中，λn是与K离子通道的时间常数相关的参数。

本文中，Vk、Vc、λn、k1为可变的控制参数，其余参数均保持不变。数值仿真所需要的参数为：gi=1 800，gkv=1 700，gkc=10，gl=7，Vi=100，Vl=-40，Vk=-75，Vc=100，kc=3.3/18，ε=0.27，λn=225.8，I=-50，k2=2.0，α=2，β=0.000 6，k2=2。

在Chay 神经元系统（1）中，快/慢动态分析基于ε（ε是一个很小的量），所以状态变量C（细胞膜内钙离子浓度）相对于其他状态变量变化速度缓慢。快速子系统由以下方程组成：

如上文所提到，产融结合是企业集团发展的必然趋势，如何选择正确的实施路径，实现产业与金融之间的业务协同、资本协同、战略协同到一个新高度。我国企业在实践中通常有以下几种实施路径：

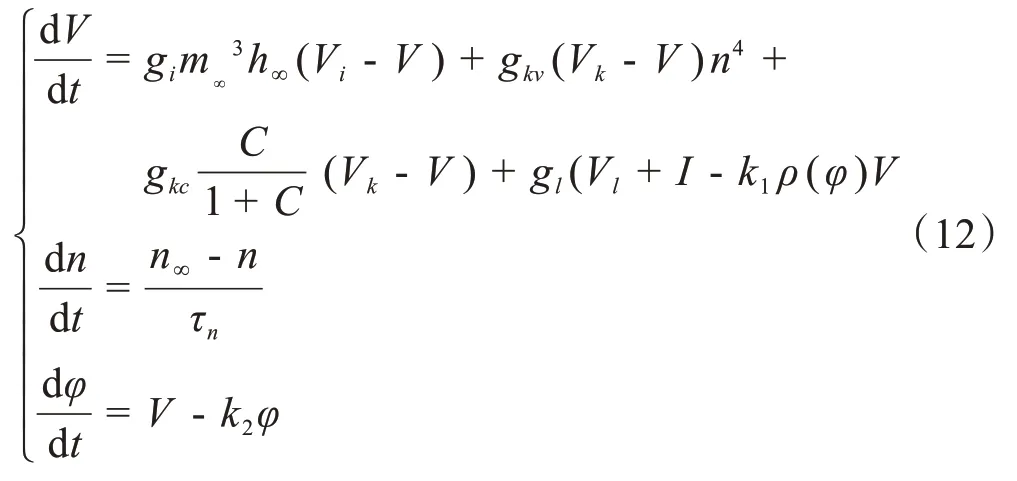
其中，将慢变量C视为快子系统的分岔参数，快速子系统的平衡点满足下列方程:

慢变量C的零斜率由dC/dt= 0给出，即

2 Chay神经元簇发类型分析

2.1 分岔曲线上分支有2个Hopf分岔点的模型

当Vk=-111，Vc=100，λn=350，k1=0.9 时，电磁效应下Chay 模型通过数值模拟得到图1。图1a 分析了系统的簇发动力学行为并对其类型进行分类。快子系统膜电位V和慢变量C的平衡点在（C,V）相平面上形成一条“Z”型分岔曲线，并附有簇发的轨迹，两个Hopf 分岔点出现在“Z”型曲线的上分支上。从图1b可以看到，系统膜电位的时间历程图呈现周期3 波动，此时系统放电正处于周期3簇放电。

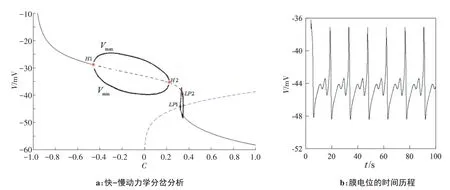
图1 分岔曲线上分支上有2个Hopf分岔点的分岔图Figure 1 Bifurcation curve with two Hopf bifurcation points on branches

快子系统的稳定焦点通过H1点处时，平衡点类型由稳定焦点转变为Hopf 分岔点，使平衡点由稳定焦点转变为不稳定焦点，同时在分岔曲线周围出现稳定极限环，稳定极限环由膜电位的最大最小值表示，出现在不稳定的焦点周围，后通过H2点经历Hopf分岔回到稳定焦点。“Z”型分岔曲线的中、下分支分别由鞍点和稳定节点组成。全局系统的平衡点是由“Z”型分岔曲线和慢变量的零斜率线（点划线曲线）的交点组成的，即LP1点，其决定簇发的产生与结束相关的所有分岔。随着慢变量C逐渐减小，分岔曲线下分支由稳定节点组成的静止状态，通过LP1点处的Fold分岔过渡到稳定焦点对应组成的上静止状态，系统进入簇发尖峰放电，随后上静止状态又通过LP2再一次经历Fold 分岔过渡到下静止状态。这一过程持续、周期、重复地引发静止态和激发态间的转换。导致系统静止态结束，激发态出现的分岔是LP1处的Fold 分岔（鞍-结分岔），而导致系统激发态结束回到静止态的分岔是LP2处的Fold 分岔（鞍-结分岔）。除了这两个导致激发态出现和终止的分岔以外，还考虑了磁滞回线的分岔［25］，磁滞回线是系统在磁感应影响下出现的闭合磁化曲线，在本文中表现为系统在慢变量参数变化时，分岔曲线由下静止态到上静止态和从上静止态再到下静止态这个过程切换发生时所对应的分岔，分别是LP1和LP2处的鞍节分岔。因此，上述簇发过程类型表现为通过“Fold/Fold”磁滞回线环表现出“点-点”簇发动力学行为。

2.2 分岔曲线上分支有1个Hopf分岔点的模型

当Vk=-75,Vc=336,λn=225.8,k1=0.3 时，在图2a 观察到，快子系统状态变量膜电位V相对于慢变量参数C的平衡点在（C,V）相平面上形成一条“Z”形分岔曲线。在图2b 观察到，电磁效应下的Chay 模型发生周期1的簇发。

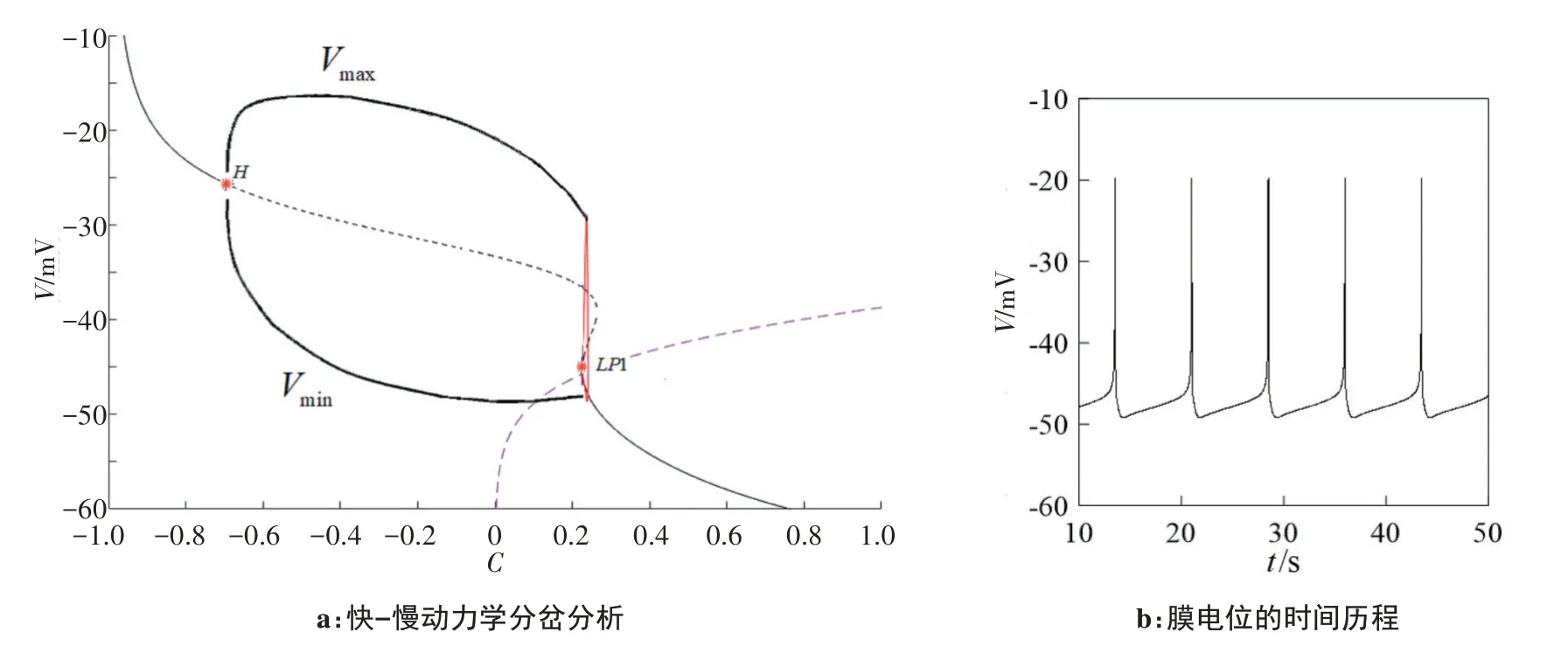
图2 分岔曲线上分支上有1个Hopf分岔点的分岔图Figure 2 Bifurcation curve with a Hopf bifurcation point on a branch

图2a中快子系统分岔曲线上分支只存在1个Hopf分岔点时，随着慢变量参数逐渐减小，经过H点系统发生Hopf分岔，稳定焦点变成不稳定焦点，且不稳定焦点周围出现稳定极限环，如图2a中环绕在分岔上分支曲线上的黑色加粗曲线。“Z”形曲线中下分支分别由鞍点和稳定节点组成。随着参数C的逐渐减小，“Z”型曲线下分支上的静止状态消失，并且通过LP1处经历Fold分岔，分岔出现伴随着不稳定焦点上方的稳定极限环消失，系统由静止态进入激发态。稳定极限环消失的瞬间与分岔曲线的中间分支撞上一个鞍，形成一个同宿轨，之后通过鞍同宿分岔系统由激发态回到静止态，导致激发态到静止态这一过程发生的分岔为LP1处的Fold分岔；导致静止态再回到激发态产生的分岔为鞍同宿分岔。另外，磁滞回线的分岔分别是Fold分岔和鞍同宿分岔。所以此处发生的簇发类型通过“Fold/同宿”环表现出“Fold/同宿”簇发。

为了将平衡点分岔和周期分岔这两种不同的方法分岔表现出的动力学现象进行对比分析，在上述参数下，利用C语言进行数值仿真得到以Vc作为控制参数的峰峰间期（ISI）分岔图3a。可以看到，Vc在区间[80,92]范围内发生变化。随着Vc值逐渐增大，系统由混沌放电转为周期放电，在较短时间内经历周期和混沌切换的状态。在Vc= 83.9 mV 时由周期2放电进入混沌放电状态，次过程伴随周期3和周期5窗口且有周期减半现象出现，在Vc=85.3 mV 时，系统发生逆倍化分岔由周期2到周期1，在此通道下由周期1直接进入混沌状态，系统呈现周期放电且夹杂着混沌放电。图3b 是图3a 在区域Vc∈[86.8,88]的局部放大图，可以看到系统在混沌放电与周期放电之间不断切换且期间不断发生逆倍化分岔。图3c 是图3a 在区域Vc∈[83.5,86]的局部放大图，可以明显看到系统处于长时间的阵发混沌放电状态，且期间不断发生周期减半的现象。图3d～f分别是Vc=81.7、81.1、87.1时系统的3周期、4周期吸引子和混沌吸引子。

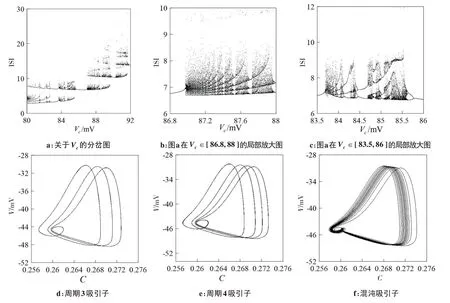
图3 关于Vc的峰峰间期（ISI）分岔图和相图Figure 3 Bifurcation curve and phase diagram of peak-to-peak interval(ISI)of Vc

2.3 分岔曲线上分支没有Hopf分岔点的模型

当Vk=-75，Vc=215，λn=500，k1=0.3 时，图4a 显示了一个简单簇发。通过快慢动力学分析，快子系统状态变量膜电位V和慢变量C在（C,V）相平面上形成一条“Z”型分岔曲线。图4b 表示膜电位的周期1 簇发时间序列。

红色曲线是叠加在分岔图上的系统相图，如图4a所示。其上、下分支为稳定焦点和稳定节点，中间分支由鞍点组成，其中LP1、LP2是Fold分岔（鞍结分岔）点。

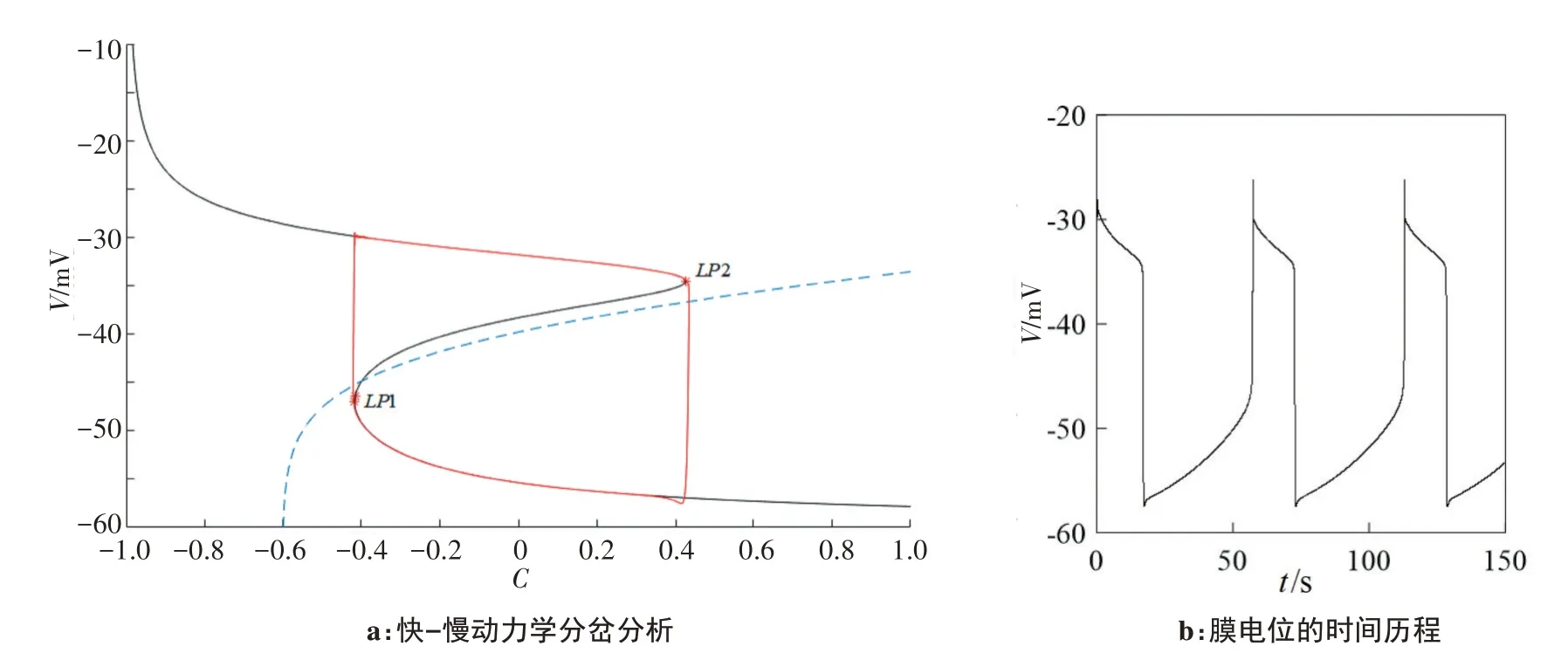
图4 分岔曲线上分支没有Hopf分岔点的分岔图Figure 4 Bifurcation curve without Hopf bifurcation points on branches

Chay 神经元系统由3 状态变量组成的个平衡点（V0,n0,C0）是由“Z”型分岔曲线与慢变量C的零斜率线组成的。因为在分岔曲线上没有Hopf 分岔点，所以不存在对应于激发态的稳定极限环，只需要讨论磁滞回线分岔。点点磁滞回线由两个静止态组成，即由稳定的焦点和稳定的上下分支结点组成稳定的上静止态和稳定的下静止态。随着慢变量参数C的减小，稳定节点的下降状态消失，并通过LP1处的Fold 分岔过渡到稳定焦点的上升状态，上态通过LP2处的另一个Fold 分岔点消失，并随着参数C的增加转变为下态。因此，簇发类型为通过“Fold/Fold”点点磁滞回线的簇发。

3 化学耦合下Chay神经元分岔分析

化学突触是神经系统中最普遍的一种信息载体，通过化学突触连接的神经元在突触缝隙中释放神经递质且被后突触神经元吸收，在这个过程中，耦合的神经元间就完成了信号的传递。化学突触可分为兴奋性和抑制性两种类型。

电磁效应下Chay耦合神经元通过化学突触连接的数学模型如下所示：

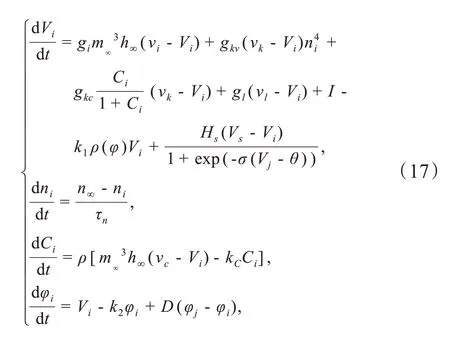
其中Vi表示组成耦合系统的两个子系统的膜电位；ni表示钾离子通道打开概率；Ci表示细胞膜内钙离子浓度；φi表示磁通量；i= 1,2，j= 2,1。Hs表示化学耦合强度；Vs表示突触的可逆电位，其取值决定化学耦合是抑制还是兴奋。θ表示突触阈值，σ表示兴奋或者抑制开始的比率常数。D表示磁耦合强度。

3.1 单参数分岔

分别以Vc，Vi，k1，k2为分岔参数，图5分别表示了ISI随着控制参数变化的分岔图。图5a可以看到Vc=50.0mV时，系统呈现周期1 峰放电，在当Vc=73.75 mV 时系统出现倍周期分岔进入周期2放电，在此通道上继续通过倍周期分岔进入周期4再到混沌放电，经过短时间的混沌放电后，发生逆倍化分岔回到周期1 放电。从图5b～d 可以看出，Chay 神经元呈现丰富的放电行为，出现类型多样的周期和混沌放电，如周期峰放电、周期簇放电、混沌峰放电、混沌簇放电，且它们彼此处于不间断的切换模式。随着分岔参数的增大，耦合神经元系统呈现复杂的放电转迁行为，表现出极其丰富的非线性动力学行为。

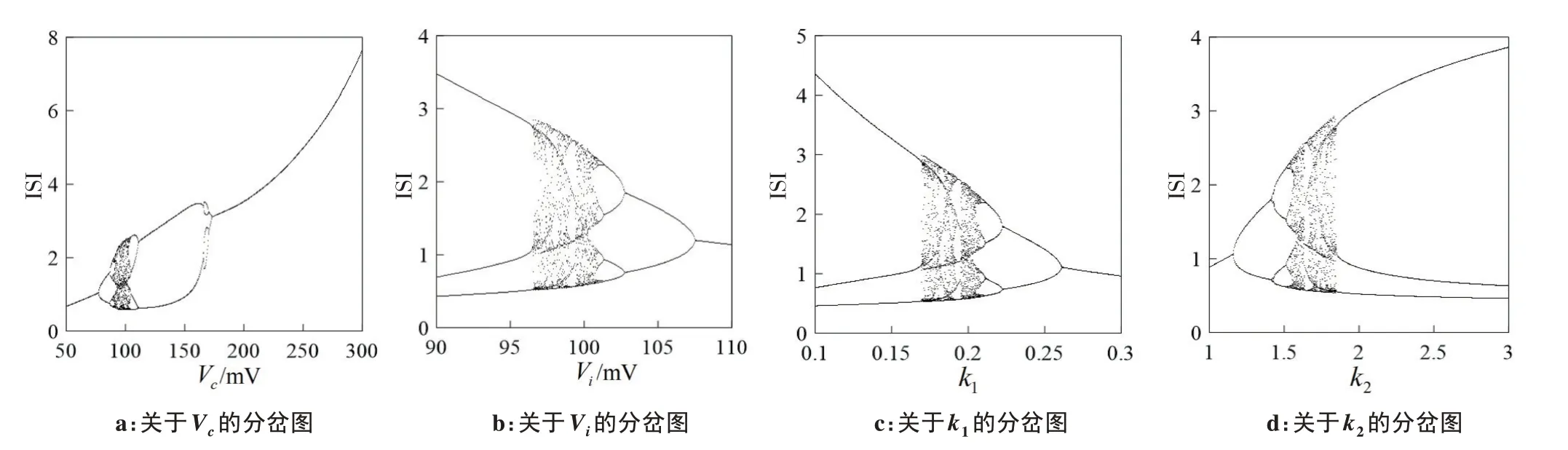
图5 单参数分岔图Figure 5 Single-parameter bifurcation diagrams

3.2 双参数分岔

双参数分岔图不仅可以显示两个参数中任何一个参数的单参数分岔性质，还可以通过放电区域判断两个参数同时变化时系统性质的改变。图6 中每一种颜色都代表一种放电周期，例如红色代表周期1放电，黄色代表周期2 放电，绿色代表周期3 放电，青色代表周期4 放电等等。图6a 是以Vi和化学耦合强度Hs为控制参数的双参数图，研究了两个参数同时变化时耦合系统的动力学变化。

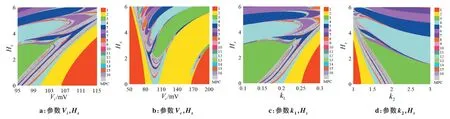
图6 双参数ISI分岔图Figure 6 Two-parameter ISI bifurcation diagrams

图中红色区域代表周期1放电，通过倍化分岔从右下角处周期1 放电依次进入周期2、周期4、周期8放电，完成倍化分岔过程，最后在周期8 处直接进入灰色混沌区域，上述过程完整呈现了通过倍化分岔进入混沌的转迁机制。后在短暂的混沌放电后发生混沌阵发现象，即混沌区中镶嵌周期5、周期6、周期7、周期8 放电，随着控制参数不断增大，混沌阵发区会结束且最终完全进入混沌区域，但是此处由于控制参数区域的局限性，并没有完全展示出阵发混沌完全进入完全混沌的过程。图6b 是在区域Vc∈［50,200］，Hs∈［0,6］内耦合系统的动力学行为。从图6b可以看出，整个放电过程是一个正方向倍化分岔过程，进入混沌区域之后又发生逆倍化分岔到周期2最终回到红色区域周期1 放电。在右下角区域Vc∈［170,200］和Hs∈[0.3,2.9]区域系统由周期2 放电直接进入短暂的混沌区，伴随周期窗口，有周期3、周期4、周期5 等。图6c 是反馈增益k1和耦合强度的双参数分岔。可以看到右下角通过倍化分岔即由周期1、周期2、周期4、短暂的周期8 之后进入混沌区域，存在阵发混沌现象，且在混沌区域还存在5周期、6 周期和8 周期窗口。然后通过加周期：周期3 依次进入周期4、周期5、周期6 簇放电，系统放电呈现出丰富的动力学行为。图6d是反馈增益k2和耦合强度的双参数分岔图，在左下角区域系统先是通过加周期倍化分岔方式从周期1、周期2、周期4、周期8 进入混沌放电状态，混沌区存在周期5窗口。其次系统又通过加周期方式在周期3 处依次进入周期4、周期5、周期6、周期7 放电状态。这种倍周期分岔与混沌交替出现的现象可以被很清晰地观测到。

4 耦合神经元的同步性分析

接下来进一步考察化学耦合强度和电磁效应对耦合系统同步性的影响。当耦合强度超过某个临界值后，系统的状态会保持几乎一致，为了定量刻画同步，引入统计量相似函数，其表达式如下所示：

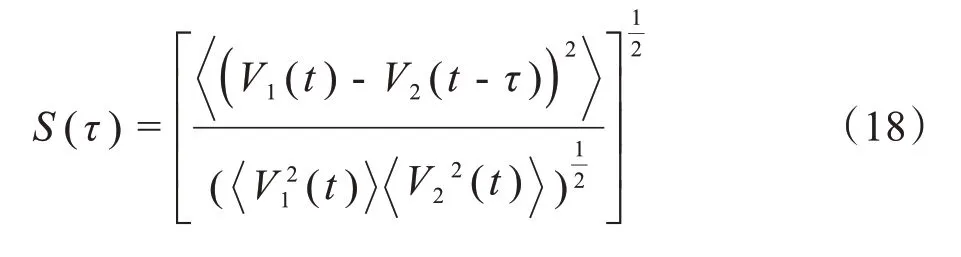
通过数值仿真，得到在不同化学耦合强度下，其统计量相似函数值的二维平面图。从图7a 可以看到，随着化学耦合强度的值逐渐增大，相似函数的值也相应处于不断变化之中。如图7a 所示，Hs∈［0.0,11.8］时，耦合系统处于完全不同步状态，图7b表示当Hs=6.4 时，耦合系统膜电位处于密集放电状态，其两个子系统膜电位相图如图7c 所示显示非同步。随着化学耦合强度的增加，当Hs∈［12.0,14.4］时，S(0)几乎接近0，耦合系统进入近似同步，例如当Hs=13.4 时膜电位时间历程（图7d）和相图（图7e）呈现出近似同步状态。当化学耦合强度继续增大，至Hs=15时相似函数值S(0)=0，这就意味着耦合系统达到完全同步状态，且此时系统处于静息放电状态，如图7f、h 所示。为了进一步观察化学突触耦合强度对耦合系统同步性的影响，离散化学耦合强度，分别取Hs=14.6、14.8、15.0、15.2，得到系统（17）关于电磁效应反馈增益系数k1，k2双参数平面的相似函数图，如图8所示。

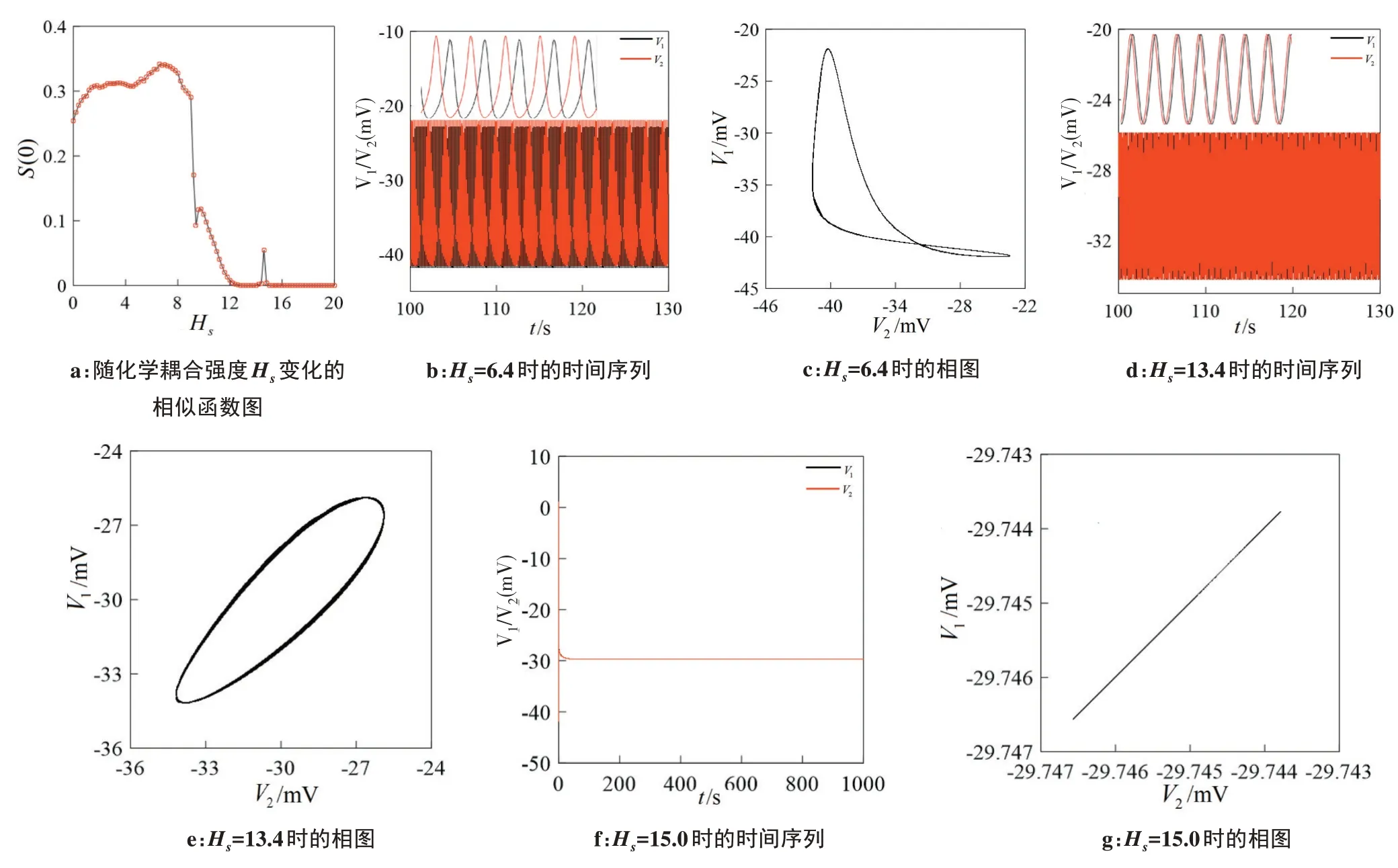
图7 相似函数图及不同耦合强度下的同步验证图Figure 7 Similarity function diagrams and synchronization verification diagrams under different coupling strengths

图8中右侧图标表示同步参数值即相似函数值，红色区域表示相似函数值为0的区域，表示耦合系统达到了完全同步。从图8a可以看到，右下角有一小块红色区域，往左上方向走相似函数值变大，系统处于不同步状态。故在参数平面（k1,k2）上，随着k1值逐渐增大，耦合系统由不同步到近似同步最后在k1=0.199 时达到完全同步。单独观察k1轴可以看到，红色区域大多数出现在右侧，只有少数的点出现在蓝色区域当中。再观察k2轴，发现在固定值k1较大时，系统会出现较短时间的同步，但当k1值较小时，随着k2的变化系统不会出现同步状态，也就是说k2对耦合系统的影响是在k1值相对较大的基础上实现的。

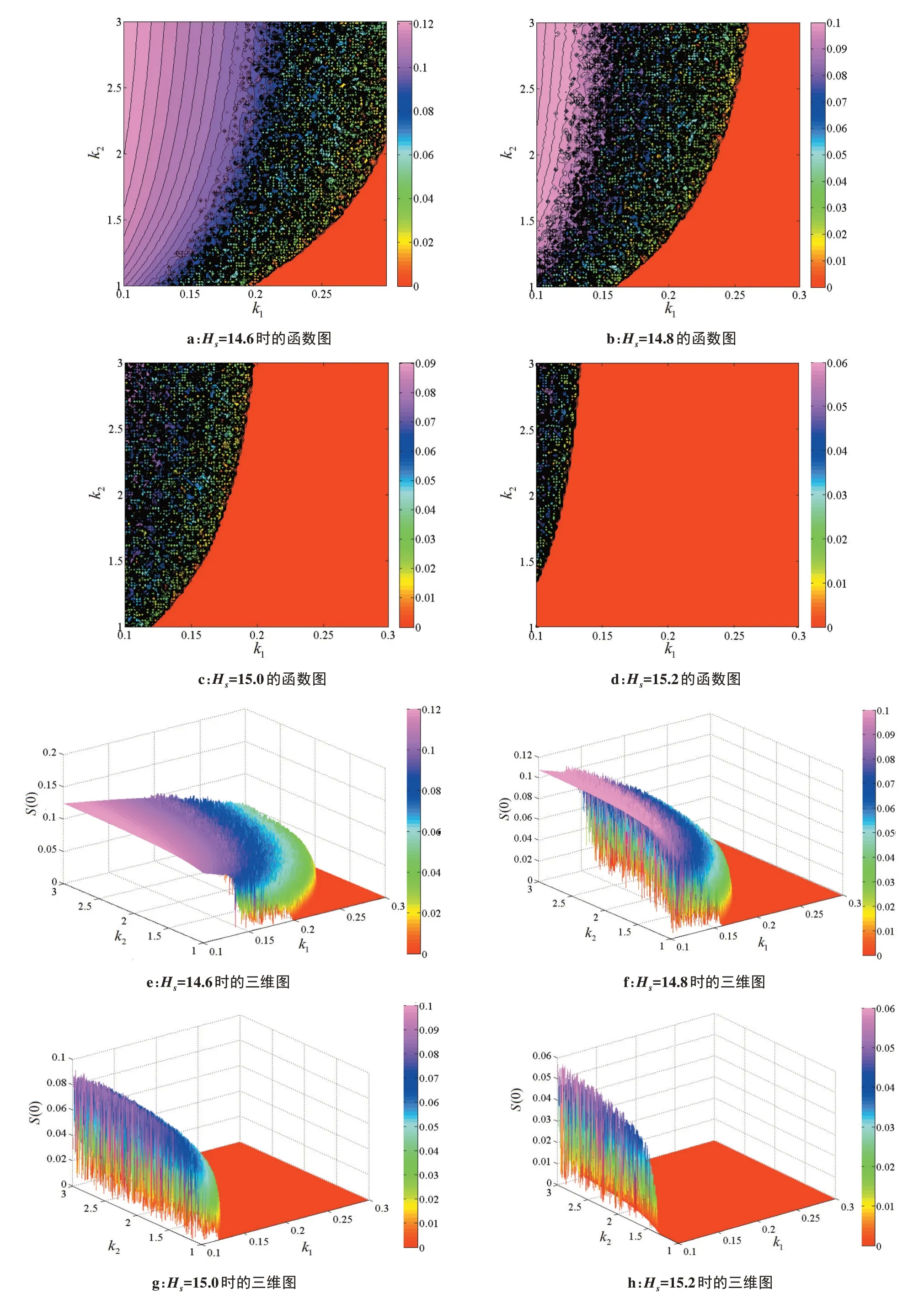
图8 不同耦合强度下的(k1,k2)双参数相似函数图Figure 8 Two-parameter similarity function diagrams of(k1,k2)under different coupling strengths

故得到结论k1对系统同步的影响大于k2。观察图8b～d 可以看出，随着化学突触耦合强度的逐渐增大，进入红色区域的k1值逐渐前移，且在双参数平面上的红色区域逐渐增大，逐渐向左上区域扩张，即在较大的耦合强度下，较小的电磁效应反馈增益系数就可以使耦合系统进入同步状态，图8e～h 是双参数同步的三维空间图形，可以更加清晰的观察到三维空间中系统的同步变化过程。其次，从图8 可以发现，化学突触耦合强度较小的变化可以使系统的同步区域发生较大的变化，即耦合强度对系统的同步影响比较大。通过离散化学耦合强度的值可以清晰的观察到耦合系统的同步转迁过程。

5 结论

本文首先基于三维Chay神经元模型，引入磁通状态变量，建立了一个四维神经元系统式（1），利用快慢动力学原理得到慢变量C关于快子系统的分岔图，以Z型曲线上分支Hopf分岔点的个数为依据，将簇发分为3种不同的类型，并对各个类型的分岔进行分析。其次研究了两个神经元通过化学突触的方式耦合构建耦合系统，通过数值仿真得到耦合系统的单参数以及双参数周期分岔图。随着各个控制参数变化，系统呈现出一系列的动力学现象，如峰放电，簇放电，混沌放电且他们之间处于不断切换的状态，其双参数分岔图中出现周期伴随混沌的阵发混沌现象。其次引入统计量相似函数，通过数值仿真，计算相似函数的值，对耦合系统的同步过程进行量化分析。通过离散化学突触耦合强度的值，观察基本参数匹配对同步的影响。研究结果表明耦合强度的微小增大，对同步会产生较大影响。耦合系统在化学突触耦合和电磁感应的共同影响下同步区域逐渐变大，为电磁效应和化学突触在神经元系统的研究提供一定的参考价值。