基于改进3D-Hénon 混沌映射的音频加密算法研究

妥永强， 巫朝霞

（新疆财经大学 统计与数据科学学院， 乌鲁木齐 830012）

0 引 言

21 世纪以来，信息成为日趋重要的生产要素。互联网具有无穷的信息获取与简易的信息交换机能，网络的全球化也使得信息的索取、传递与交换更加便捷。 如今，网络化信息已渗透于社会生活的方方面面，在经济、政治、艺术和科学等领域应用广泛。于此同时，人们对信息隐私安全也提出了更高的要求，信息隐私安全受到了严峻的挑战。 传统的加密技术只适用于文本加密，不适用于数据量大、冗余度高的音频加密，所以寻求高质量的音频加密技术具有重大的研究意义。

近年来，由于混沌系统表现出优良的初值敏感性、遍历性以及不确定性，国内外许多学者将其广泛运用于图像加密以及音频加密领域。 如：文献［2］中将Arnold 映射扩展至维空间后得到高维混沌映射，从而构建了混沌查找表，使用密码区块链模式将其应用于音频加密。 但该算法实现难度较高，具有一定的局限性。 文献［3］利用Logistic 混沌映射构建映射关系进行音频的置乱加密。 该算法虽然降低了复杂性，但秘钥空间较小，抵抗统计攻击性能较差，易被破解。 针对上述问题，文献［4］中设计了基于多涡卷混沌系统的音频加密算法。 该算法的初始秘钥同时取决于音频的Hash 值和外部密钥，在增加秘钥空间的同时，有效提高了选择明文攻击与统计攻击的难度。 文献［5］利用随机矩阵对音频信号进行扩充后，通过Logistic 混沌映射，分别在时域、小波域、时域对音频进行加密。 文献［6］利用细胞神经网络混沌与Logistic 混沌映射构造出多级秘钥后，通过Logistic 混沌映射对音频进行加密。

本文在上述研究的基础上，提出了一种将改进的3D-Hénon 混沌映射与离散化超混沌系统相结合的多混沌音频加密算法，并给出了仿真实验结果以及安全性能分析。

1 混沌系统

超混沌Chen 系统

4 维超混沌Chen 系统，其定义如式（1）：

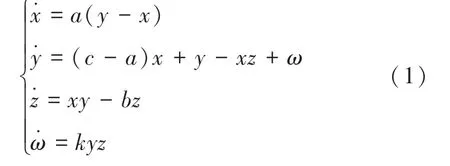
其中，10；83；38；是一个01 之间的参数。

本文选取0.02，此时系统的4 个Lyapunov指数分别为：0.969，0.042，-12.67，0。 其中有两个正指数，说明该系统是超混沌系统。 使用四阶Runge-Kutta 算法对式（1）离散化（时间间隔0.02），得到超混沌Chen 系统部分相图如图1 所示。

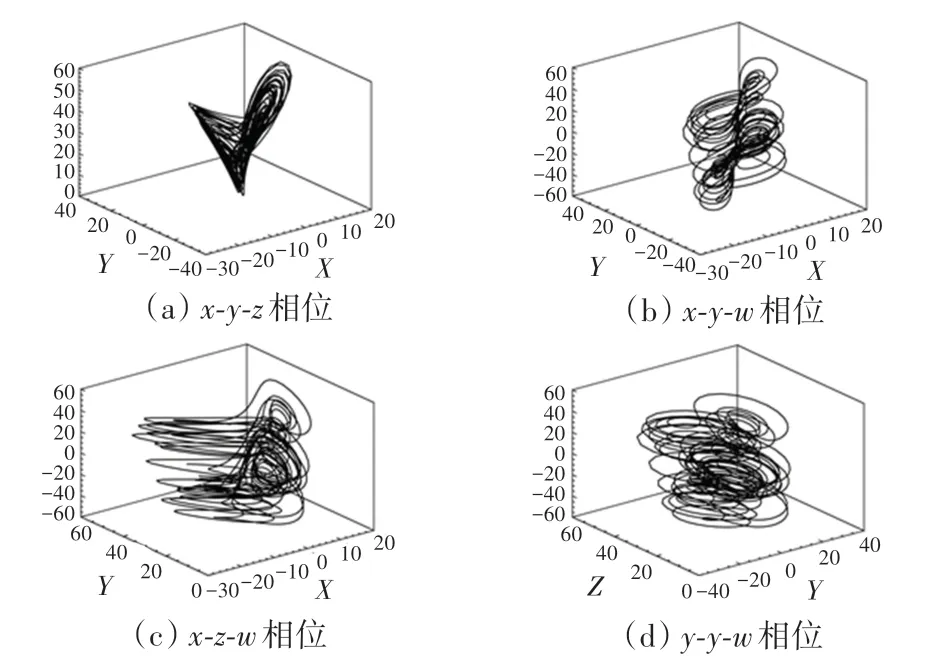
图1 超混沌Chen 系统吸引子相位图Fig. 1 Attractor phase diagram of hyperchaotic Chen system

改进的3D-Hénon 映射混沌系统

1976 年，法兰西数学家Hénon 受Pomeau 关于洛伦兹系统数值结果的启发，通过对（，） 平面自身的3 个映射链来模拟，并调节参数得出的二维映射，作为一种简单的高维混沌映射，具有优良的非线性动力学特征，其定义如式（2）：

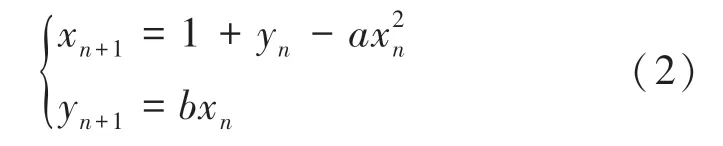
其中，、为二维Hénon 混沌映射的控制参数。

图2 为参数03，初始值为015，0.25时的Hénon 混沌映射混沌轨道图及分岔图。 通过分岔图可得出：当参数106122 或127129 或131142 范围内时，其处于混沌状态，系统有正的最大Lyapunov 指数。

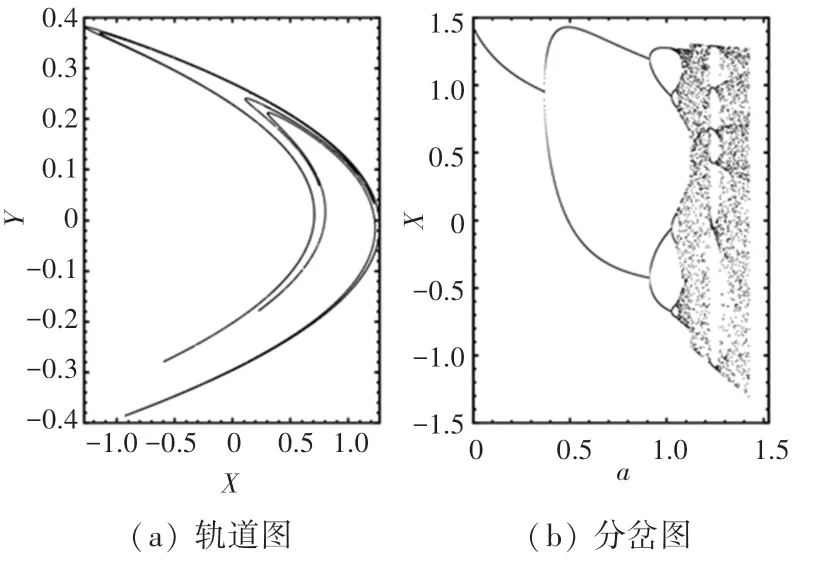
图2 Hénon 映射的序列轨道图与分岔图（a ＝1.4）Fig. 2 Sequence track and bifurcation diagrams of Hénon mapping

通过对式（2）进行调整及改进，添加变量及控制参数、， 得到改进的3D-Hénon 映射。 其定义如式（3）：

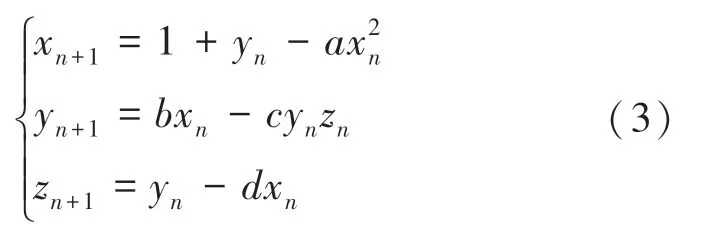
其中，、、、为3D-Hénon 映射的控制参数（03，01，2）。 图3 为初始值为02，01，0.3 时改进的3D-Hénon 混沌映射混沌轨道及三维分岔图。同样，当参数106122或127129 或131142 范围内时，处于混沌状态，系统有正的最大Lyapunov 指数。

图3 改进3D-Hénon 映射的序列轨道图与三维分岔图Fig. 3 Improved 3D Hénon map sequence orbit diagram and 3D bifurcation diagram

Lyapunov 指数是利用数值方法描述非线性动力学系统稳定性的一种重要方法，是衡量非线性动力学系统在其相空间中沿某方向运动过程中各轨道之间相互靠近与远离的一种指数级度量，提供了混沌系统动力学行为的定性和定量特征。 当非线性动力学系统为离散映射系统时，若最大Lyapunov 指数为正时，其具有混沌行为。 图4 为改进的3D-Hénon映射在控制参数、变化时，01，2，初始值02，01，0.3 时的Lyapunov 指数图。

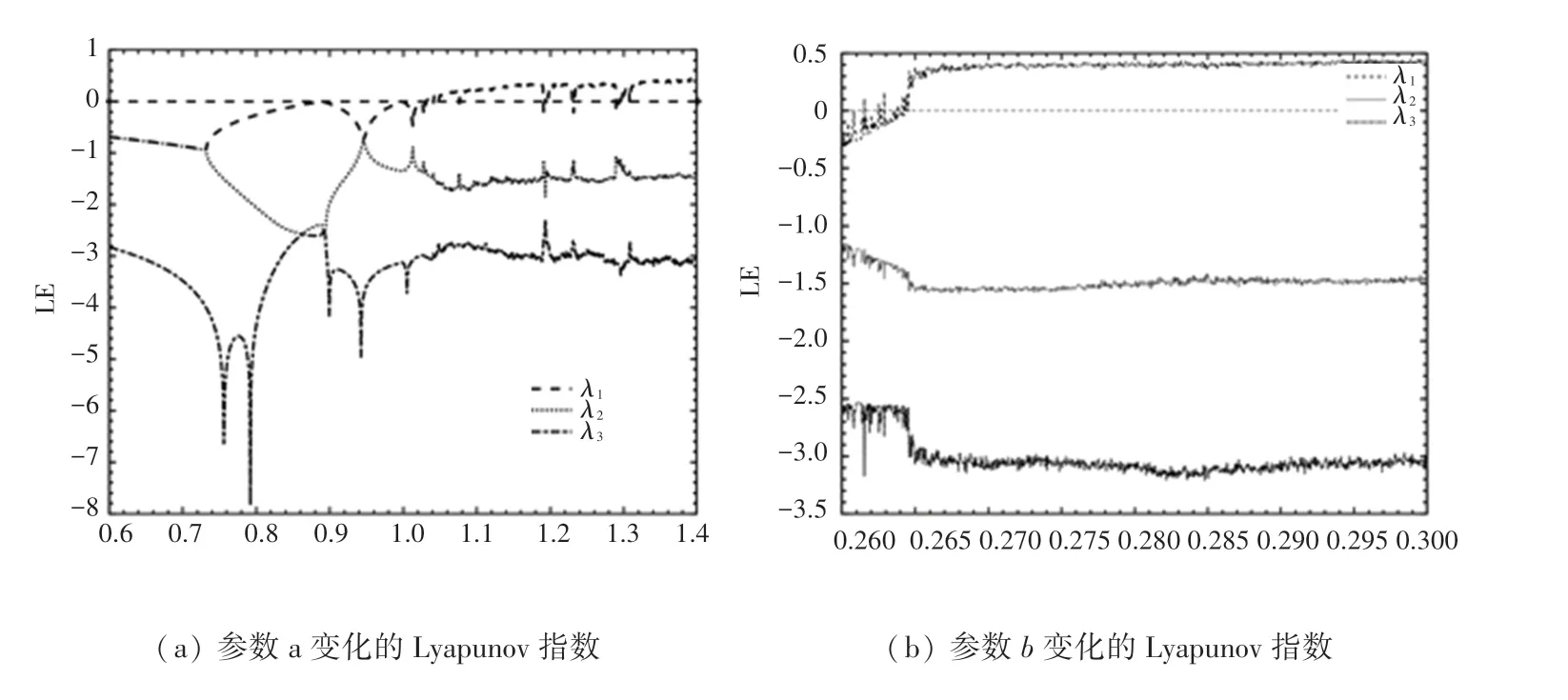
图4 改进3D-Hénon 映射当参数变化的Lyapunov 指数图Fig. 4 Lyapunov exponent plot for improved 3D-Hénon mapping when parametersa andb vary

由图4 可以看出， 当参数106122 或127129 或1311.42 范围内时，其最大Lyapunov 指数大于0，系统处于混沌状态。 当参数14，026503 时，最大Lyapunov 指数恒为正，其对参数具有鲁棒性，该混沌系统适合产生用于音频加密的随机数。

2 加密算法设计

2.1 音频预处理

取时长秒的音频进行采样率为（Hz） 的采样后得到（） （1，2，…，），作为明文音频的音频数据。 对音频信号进行分块处理步长为，超出部分用0 填充，则原始音频信号被分为或1块。 设（），（1，2，…，） 为原始音频信号分块中的一块， 分离左右声道a（） 与a（）。 将音频信号振幅放大后，进行坐标系偏移， 取整得到增强后的信号序列α（），α（）。

2.2 密钥的选取与生成

（1）用户任意选取3 个0～1 之间的数值作为初始密钥0(，，) ；

（2）将初始密钥0 作为初始值输入改进的3D-Hénon 映射，预迭代系统次，以消除其暂态效应，增强系统初值敏感性。 继续迭代次生成随机序列：mod（）为取余函数；为足够大的正整数。

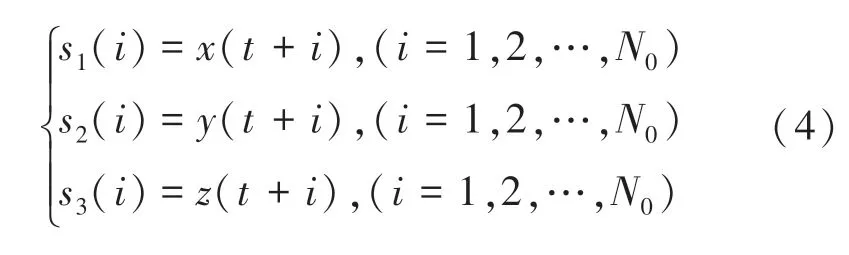
2.3 随机数发生器

表1 为伪随机序列的NIST sp800_22 随机性测试结果。 可以看出，待测试序列的_值均大于0.01全部通过测试。 可以认为文中序列是随机序列，适合作为后续加密过程的加密密码。

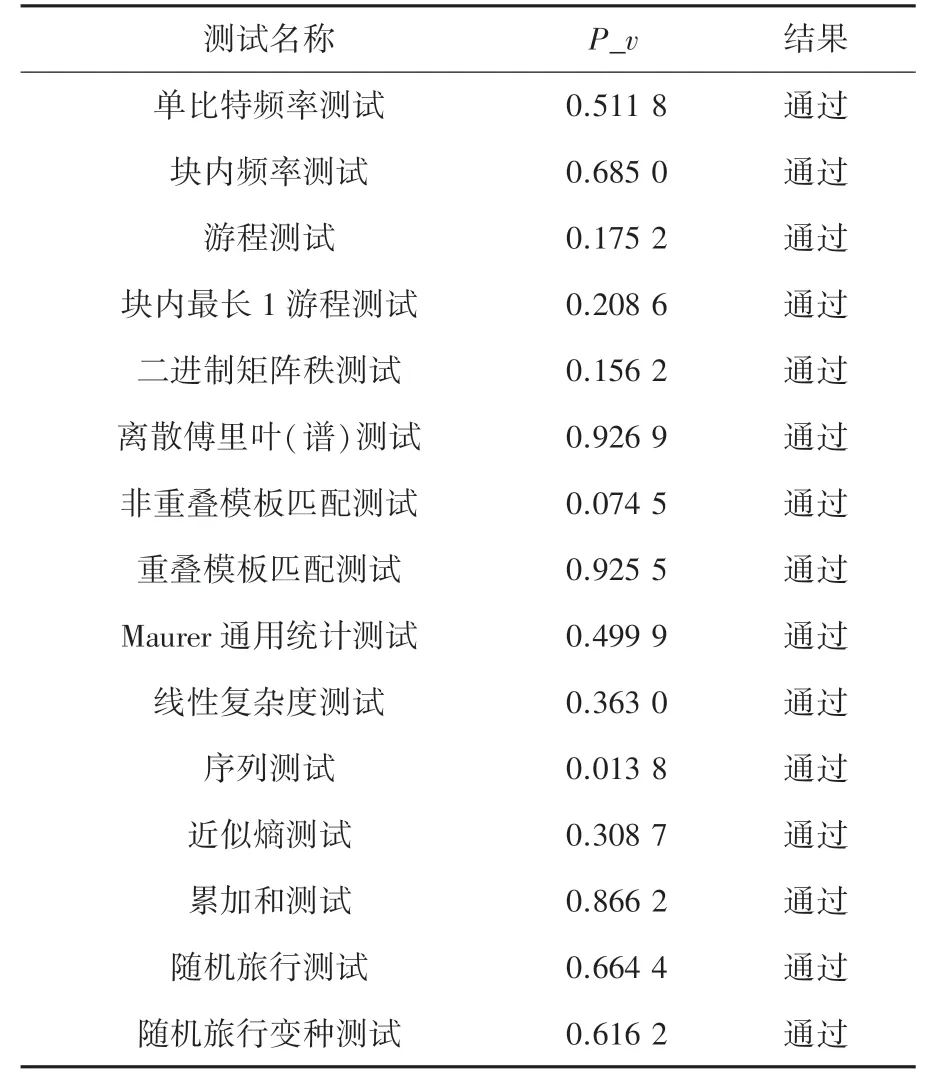
表1 NIST sp800_22 随机性测试结果Tab. 1 Randomness test results of NIST SP800 22

2.4 循环排序置乱算法

将序列F（1，2） 中的每个序列对3、7 取余，分别提取余数为0 的序列和剩余序列，按照“先升序后降序”的规则进行排序，得到6 条索引序列In，（1，…，6）。 将6 个索引序列进行分组，定义如下规则，得到新索引序列：index＝［εβδ］。

（，） 表示行列的全1 矩阵。

分别对序列α（）、α（） 进行置乱。 置乱时每个元素依次循环索引序列的初始位置、1／3 位置、2／3 位置处置乱。 置乱规则，是将（） 元素与(index()) （1，2，…，） 元素调换位置。 分别对所有序列置乱后，得到置乱音频序列α（）、α（）。

2.5 扩散算法

对置乱后的序列进行向前扩散与向后扩散。 扩散规则如下：

4)警报声：当本系统进行实时监控的时候，如果视频中出现火点，该系统会向正在监控的工作人员发出报警声，毕竟人的精力是有限的，有时难免会出现一些错误，但该系统就很好地弥补了这一点，使森林出现火灾的时候能够第一时间让工作人员了解这一信息，迅速地将火势控制住。

通过式（7）对置乱音频扩散得到加密音频序列C、C，合并后得到加密后的音频。 音频加密流程如图5 所示：

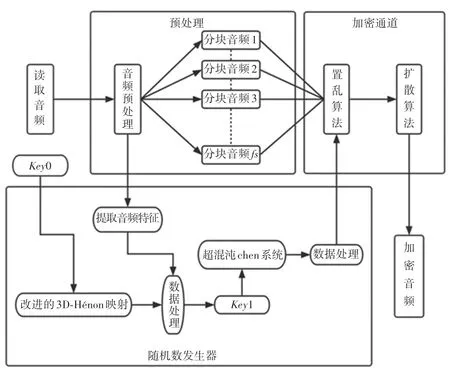
图5 音频加密流程图Fig. 5 Flow chart of Audio encryption

3 实验仿真与性能分析

3.1 实验仿真

实验仿真采用双声道音频“Audio1.wav”，分别截取其中一块进行实验仿真。 实验参数分别设置为：2，30 000，8 000，0（0141 592 6，0653 589），1（0969 015，0409 086， 0622 289，0640 965）。

图6（a）～6（c）分别为原始音频波形图、加密音频波形图、解密音频波形图。 可以看出，加密后的音频波形图呈现无规则杂乱状，已与原始音频无任何关联，经解密后的音频波形图与原始音频波形图完全相同。

图6 音频加密仿真实验结果Fig. 6 Audio encryption simulation results

3.2 密钥敏感性与密钥空间分析

相对于原始秘钥，一个细微差别的密钥，其解密后的差别也非常大。 测试中， 在原始秘钥中选取0 中一个值增加10，即0（0141 592 610，0653 589） 对加密音频进行解密。 解密后的音频时域波形图杂乱无章，得到完全错误的解密音频，无法识别出原始音频的信息，如图7 所示。 对于一个安全的加密算法，其密钥空间大小至少超过2才算是安全有效的加密算法。 本文加密算法中共有2 组7 个秘钥，密钥空间为 (10)22，密钥空间足够抵御穷举攻击。

图7 错误秘钥解密音频时域波形图Fig. 7 Wrong key decryption audio time domain waveform

3.3 抗统计攻击性能分析

3.3.1 语谱图分析

音频的语谱图将整个音频范围用不同的颜色记录，这些颜色表示特定时间、特定频率与能量之间的关系。 图8（a）、（b）分别显示了原始音频与加密音频的语谱图。 表2 为原始音频与加密音频能量分布描述统计，原始音频能量均值为-102.488 4 dB／Hz，其标准差较大，变异度为81.25%，分布离散，原始音频信号语谱图中能量分布不均匀，其包含较多信息量。 而加密音频能量的均值为-50.764 5 dB／Hz，标准差不大，变异度为11.24%，表明加密音频能量均匀分布在-50.764 5 dB／Hz 附近，几乎不包含原始音频信息，音频整体平均能量分布也被拉高，接近噪声，可以抵御基于音频语谱图的统计攻击。

3.3.2 信息熵分析

一条信息所包含信息量的大小取决于信息的不确定程度，而其不确定程度与复杂度由信息熵来量化。 信息熵数学定义为：

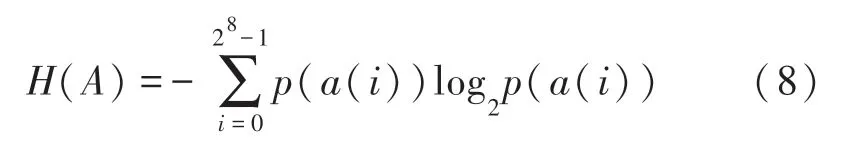
信息熵越大，则信息的不确定程度与复杂度越大。 加密后的音频数据信息熵越接近8，加密效果越好，音频越接近于噪声，攻击者获取的信息越少。

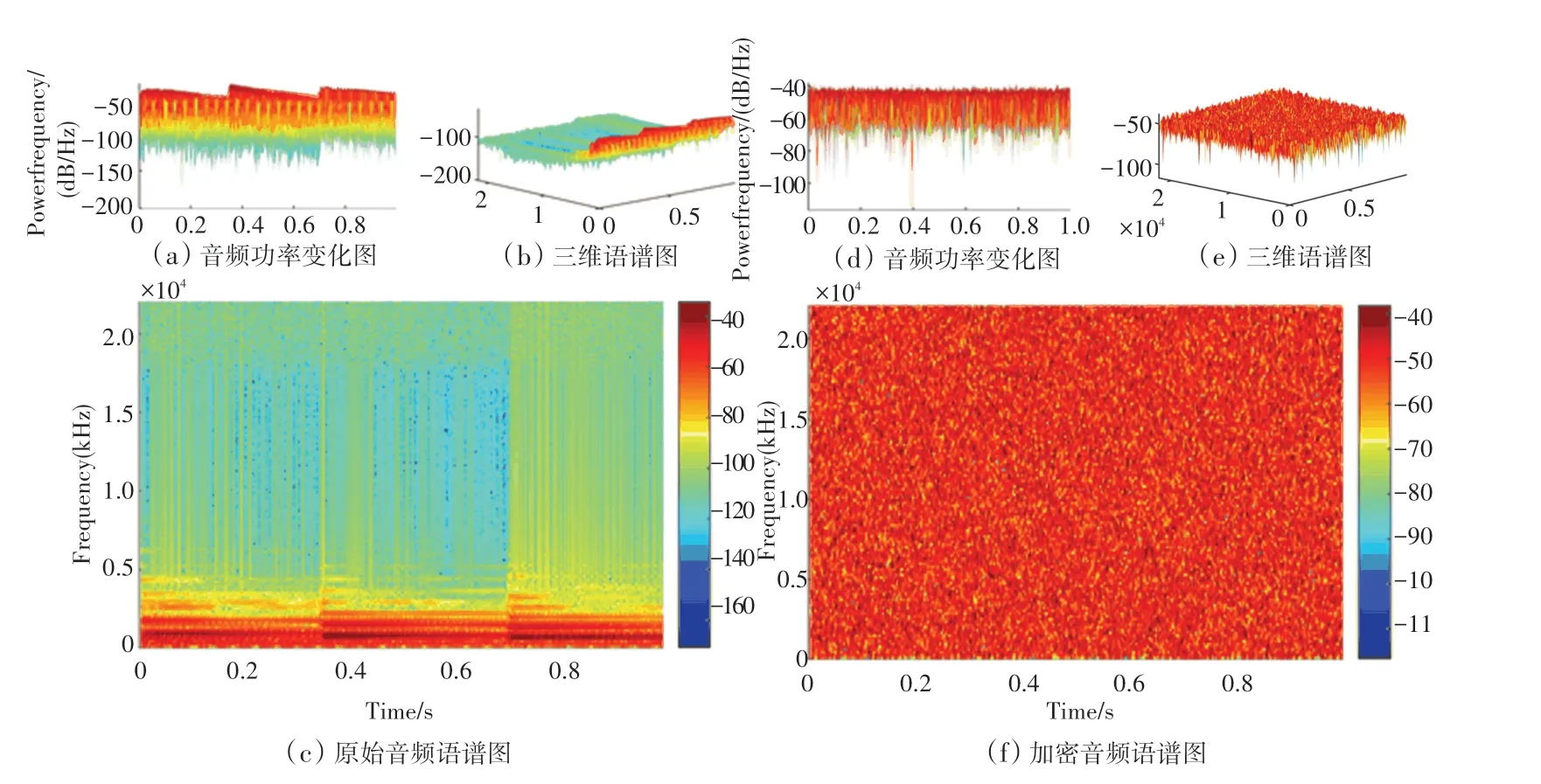
图8 原始音频声与加密音频声谱图Fig. 8 Original audio encrypted audio spectrogram

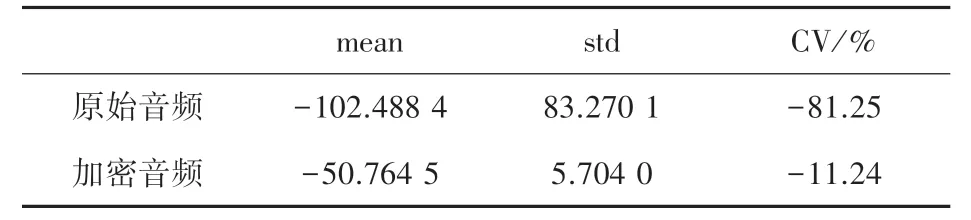
表2 音频能量分布描述统计表（dB／Hz）Tab. 2 Description of audio magnitude distribution

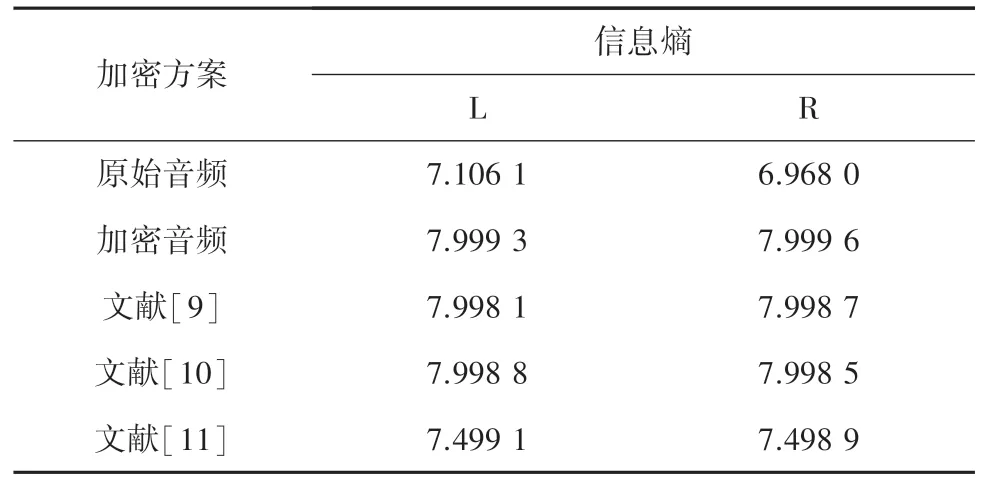
表3 信息熵对比表Tab. 3 Comparison table of information entropy

加密音频数据整体在区间内概率分布越均匀，加密音频的抗统计攻击性能越优。 直方图横轴为分布区间，纵轴为对应的频数或频率。 图9 分别为原始音频与加密音频频数分布直方图。

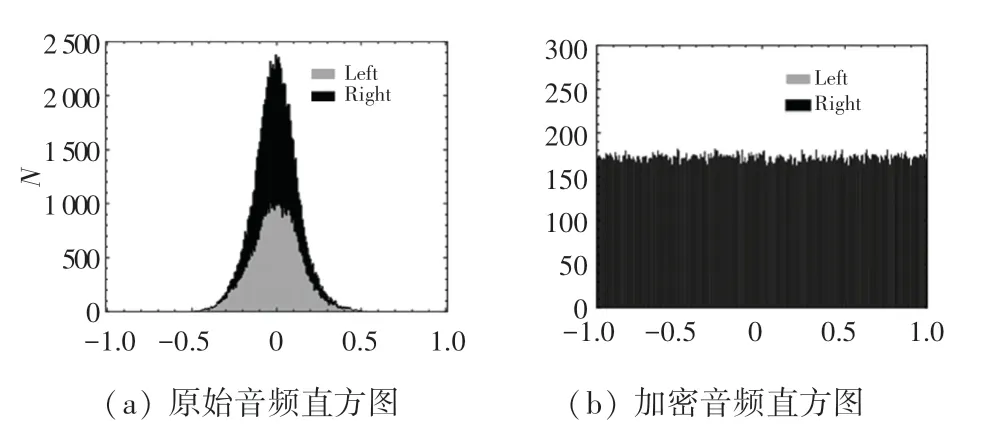
图9 原始音频与加密音频直方图Fig. 9 Histograms of raw and encrypted aud

由图9 中可以直观的看出，原始音频的频数分布近似正态分布，而加密音频的频数分布均匀，很好的隐藏了原始音频的统计特性，攻击者不易通过分析密文直方图获得信息，从而能够抵抗基于直方图的统计攻击。

3.3.3 相关性分析

加密音频相邻采样数据之间相关系数越小，说明数据的混乱与复杂程度越大，因而加密安全性更高。 音频相邻幅值间相关系数计算公式如下：

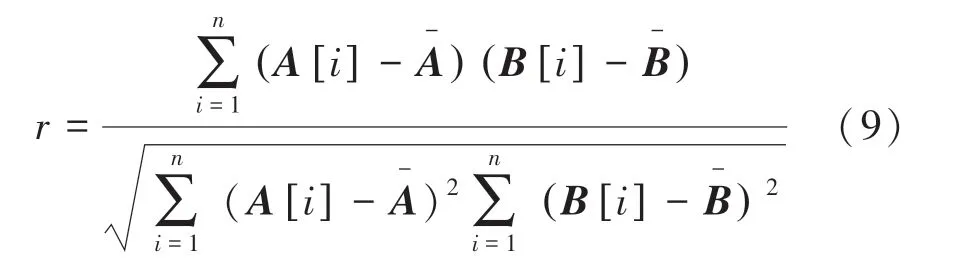
其中存储向量［］ 和［］ 表示第对相邻音频信号值，为总对数。 随机选取10 000 对相邻音频数据进行测度。 图10 为明文音频与加密音频相邻幅值散点图，图中可以看出明文音频左右声道相邻音频信号值之间呈现出明显相关关系，而加密音频相邻音频信号值之间无相关关系，表4 为相邻音频信号相关性对比表，表中明文音频左右声道相邻信号值相关性为正相关关系数值分别为0.994 3 与0.997 2，而加密音频左右声道相邻信号值相关系数分别为0.000 7 与-0.000 3 接近于0 表明其无相关关系，通过与其他文献对比文中加密算法加密后的音频混乱与复杂程度大，攻击者不易通过分析相关性操作得到明文音频信息. 表明加密算法能够很好的抵御基于相关性的统计攻击。

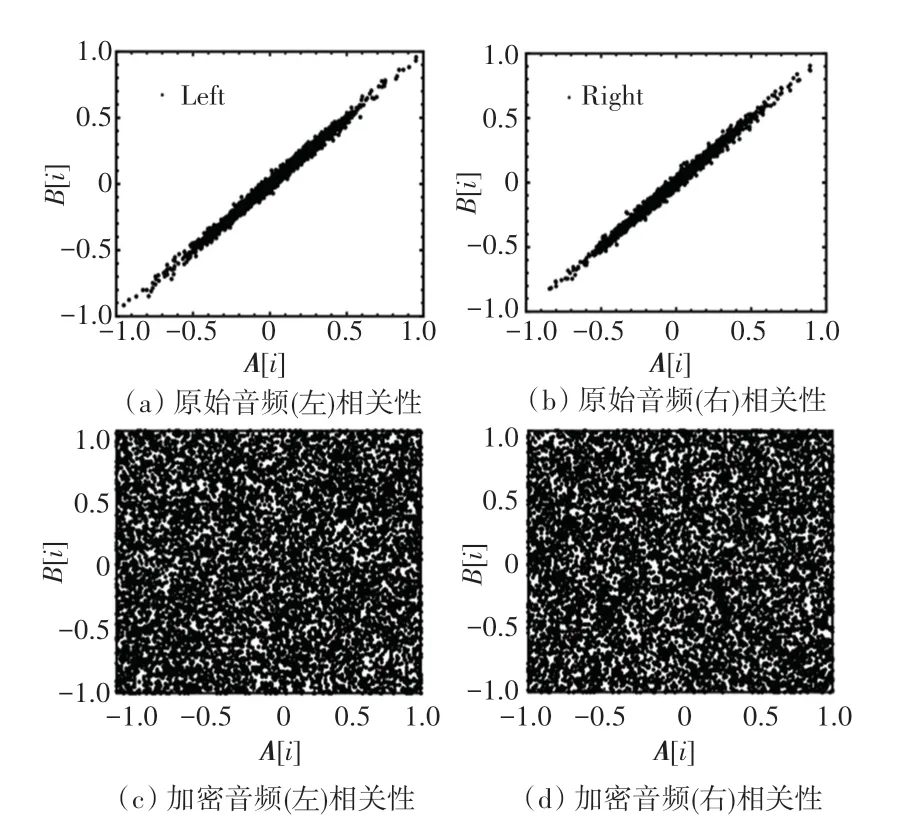
图10 明文音频与加密音频相邻幅值散点图Fig. 10 Adjacent amplitude scatter plot of plain-text audio and encrypted audio

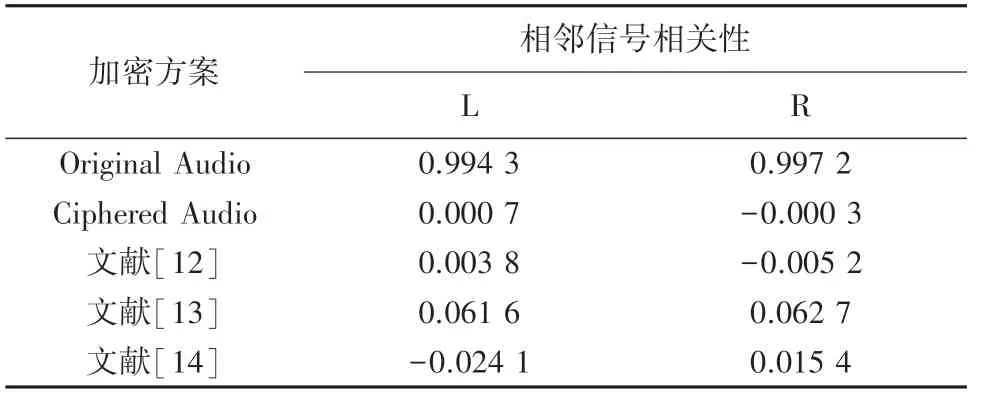
表4 相邻音频信号相关性对比表Tab. 4 Correlation comparison table of adjacent audio signals

3.3.4 峰值信噪比分析（）

峰值信噪比为音频信号最大功率与噪声音频信号功率的比值。 峰值信噪比常用作确定信号压缩质量，数值越大，信号压缩质量越高，越接近原始音频。若加密音频与明文音频峰值信噪比越低，则加密音频与原始音频差异越大，加密后的音频越接近噪声。峰值信噪比通过均方误差（） 来定义，均方误差反映了两组信号之间的差异程度。 均方误差与峰值信噪比的计算如下：

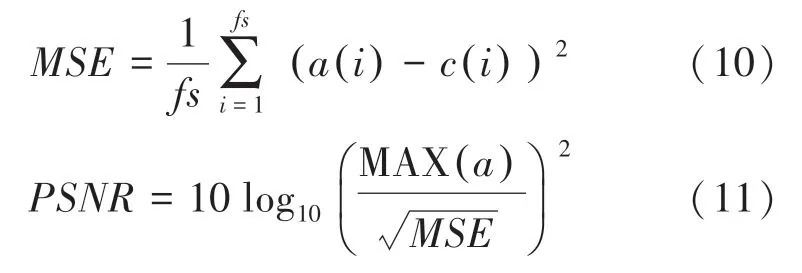
其中，（） 为原始音频序列，（） 为加密音频序列。

表5 中列出了随机选取的5 段加密音频测试结果。 可以看出，加密后的音频在不同长度下左右声道的峰值信噪比都较低，加密音频与原始音频差别较大，加密后的音频很好的隐藏了原始音频的信息，表明该加密算法能够很好的抵御基于峰值信噪比的统计攻击。

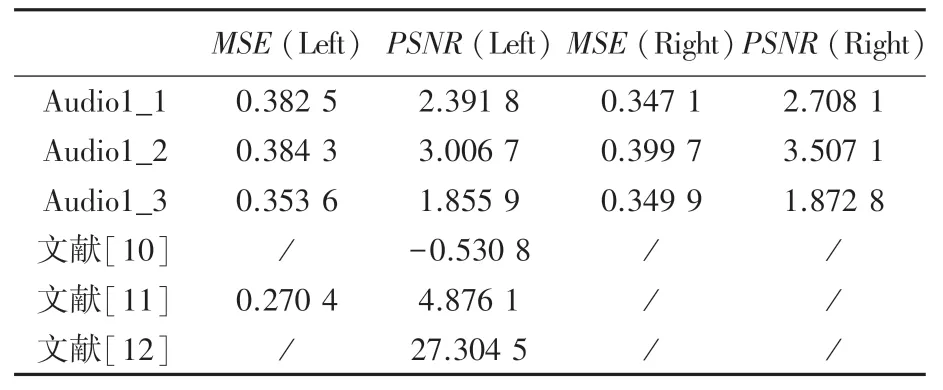
表5 加密音频PSNR 测试结果表Tab. 5 Test results of encrypted audioPSNR

3.4 鲁棒性分析

3.4.1 抵抗差分攻击性能分析

攻击者通过对原始音频进行细微差别的改变，分析加密音频之间映射出的差异情况，这种类型的攻击称为差分攻击。

在数据加密中对差分攻击的抵抗性能一般通过样本数变化率（） 和统一平均变化强度（） 进行分析。

是对加密算法质量的鲁棒性检验，测试目的是原始音频和对应加密音频间不同样本数量在样本总数中所占比例的比较。 计算公式如式（12）：

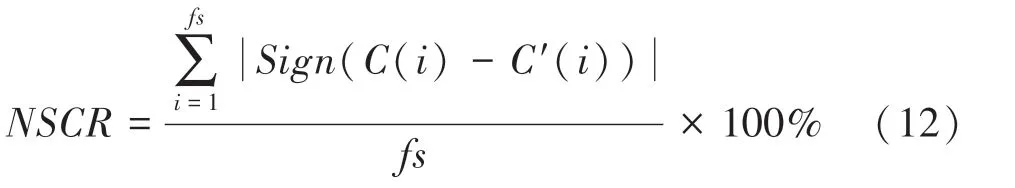
其中，（） 为未改变原始音频的加密音频序列；（） 为随机改变一个原始音频采样数据的加密音频序列；（） 为符号函数。

是记录原始音频与加密音频相应位置差值与最大差值间比值的平均值，计算公式如式（13）：

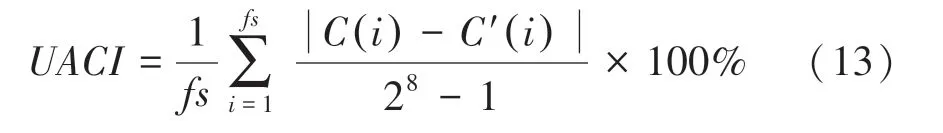
当音频信号为8 bit 时，加密算法抗差分攻击的和的最优值分别为100和33333。

表6 为随机测试30 000段加密音频的和平均值对比。 通过与其它文献对比分析表明：本文音频加密算法得到的与更加接近理想值，加密算法的抵抗差分攻击性能较强。

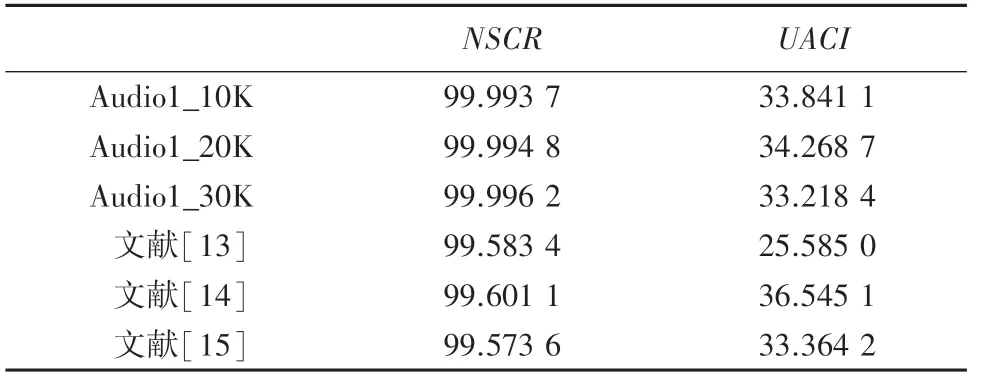
表6 随机测试NSCR 和UACI 平均值对比Tab. 6 Comparison of average values ofNSCR andUACI in random tests %

3.4.2 抗噪声性能分析

当攻击者进行主动攻击时，对密文加入噪声，解密信息质量会大幅度下降。 加密算法的抗噪声性能越好，在密文受到噪声攻击时，解密后还原出原始音频的信息越多。 在密文传输中，当攻击者对密文进行剪切攻击时，鲁棒性较差的算法在受到攻击后，密文解密后明文的关键信息会丢失，导致信息无法成功传输。 优秀的算法在受到剪切攻击，密文解密后可解析的信息应尽可能多，而能够保留明文的关键信息。 图11 为加入5%的椒盐噪声解密后的音频时域波形图。

图11 加入5%椒盐噪声的解密音频时域波形图Fig. 11 Decoded audio time domain waveform with 5% salt and pepper noise

由图中可以看出，在加入5%椒盐噪声的情况下，解密后的音频时域波形质量较高，可以轻松被人耳所识别，解密后的音频依然能够恢复大部分信息。计算加入椒盐噪声后，解密音频与明文音频的峰值信噪比可以以数值形式量化音频加密算法的抗噪声性能，计算得到左右声道的均方误差分别为：7.911 0E-04、6.595 3E-04。 解密音频左右声道峰值信噪比分别为：25.944 0、25.246 8。 计算得到的均方误差较低，解密后音频质量较高，加密算法具有良好的抗噪声性能。

4 结束语

本文通过对二维Hénon 混沌映射进行升维与改进得到改进的3D-Hénon 混沌映射，并将其与离散化的超混沌Chen 系统相结合，生成的伪随机序列用于音频加密。 预处理过程将原始音频信号进行分块处理提升了运行效率，利用生成的伪随机序列进行循环排序置乱以及向前向后扩散完成加密。 其中秘钥与明文音频互相关联，实现了“一次一密”，降低了选择明文攻击的可能性。 通过仿真与分析结果表明，提出的音频加密算法具有较强的秘钥敏感性和足够大的秘钥空间，加密后的音频能量分布均匀，相邻振幅间相关性较低，与明文音频的峰值信噪比较低，加密算法具有良好的抗统计攻击性以及鲁棒性。