动态图染色问题研究
2022-05-06邱雅娴郝元宵周军锋
邱雅娴, 郝元宵, 周军锋, 杜 明
(1 东华大学 计算机学院, 上海 201620; 2 燕山大学 信息科学与工程学院, 河北 秦皇岛 066004)
0 引 言
图染色是指为无向图中每个结点分配一个颜色,使得图中任意两个相邻结点具有不相同的颜色。 图染色问题应用广泛,是学术界的热点问题之一,可用于核酸序列设计、交通管理、网络频道分配、社团体检测等方面。 现实中的图更新频繁,静态图染色算法无法使用,因此研究者们将目光投向动态图染色问题上。
对于静态图染色问题,目前效果最好的是Global 算法。 此方法按度大小降序,对结点依次染色,每个结点使用邻居结点未使用的颜色。 动态图染色算法主要有:基于色彩饱和度的DCLocal、基于OC 图的DC-Global、基于bucket 分层的Small-buckets 算法与Big-buckets 算法等等。 其中,DC-Local 依据贪心策略进行结点着色,该方法会导致色数(色数为染色过程中需要使用的最小颜色数量)快速增加。
DC-Global 基于贪心策略,优先选择度大的结点进行染色,每次仅处理一条更新边,处理效率较低。 Small-buckets 与Big-buckets 算法基于桶分层思想,将图中结点划分到一组桶中,桶中结点对应的子图单独染色。 该方法在图更新时,不会重新调整相邻结点颜色,导致使用的色数较多,染色质量较低。
本文针对现有动态图染色算法效率低下的问题,提出了基于批量处理的染色算法,即一次处理所有的更新边(包括新增边和删除边);而针对现有动态图染色算法空间消耗大的问题,在保证染色质量的前提下,提出了去掉索引、降低内存消耗的算法。最后,基于真实数据集,将本文算法与现有算法从染色质量、染色效率、内存消耗3 个方面进行比较,用以验证本文算法的有效性。
1 背景知识
1.1 相关定义
问题定义:给定图和一组新增边和删除边的操作,求得最佳图染色()。
结点的度:给定图(,),其中是顶点集,是边集。 无向图中,用() 表示结点的度。
全序排序:给定图的两个结点和, 当()() 或()(),且()() 时,记作≺,称为全序排序。
OC 图:给定图(,),其OC 图记为。是指对于图中的任意一条边(,) ∈, 如果≺,则中有一条从到的有向边,否则,中有一条从到的有向边。
图染色:图的图染色是一个映射函数:→。 其中代表颜色集,并使得任意两个相邻结点、满足() ≠()。()表示中所使用的颜色数量。 对于一个结点∈,用() 来表示通过函数指定的颜色。
色数:色数是指对图染色所需的最少颜色数,记做()。
最佳图染色:指对于图,使得()()的染色。 其中,() 指对图染色的结果。
1.2 相关算法分析
目前存在的3 种动态图染色的研究成果如下:
(1)DC-Local。 基本思想:新增边(,) 时,若结点、颜色相同,则对其中色彩饱和度小的结点重新染色;删除边,() 时,对结点、都重新染色。 重新染色时,尽量减少颜色避免颜色增加。由于只修改更新边的邻接结点及其附近结点,导致该方法无法减少总色数,染色效果差。
(2)DC-Global。 此方法针对新增边和删除边,分别采用DC-Orient-Ins 和DC-Orient-Del 进行处理。 新增边(,) 时,将颜色可能会变的结点加入优先队列中,按全序顺序排序。 若存在某个结点其多个射入结点的颜色都改变了,则该结点被重复染色。 删除边(,)时,将待染色结点加入中,初始候选染色结点为{,},中任意结点颜色改变时,其所有射出结点需全部加入中。
DC-Global 处理一条更新边的时间复杂度为(n·log(n))。 其中,n为更新该边后需要重新染色的结点数目;空间复杂度为(),为边数,为结点数。 该算法的空间复杂度高,效率低。
(3)Small-buckets 和Big-buckets 算法。 这两种算法在色数消耗与图更新后需要重新着色的结点数上做权衡,是一组互补算法。 算法思想为:划分为一组桶,将图中结点映射到桶中,每个桶中包含一组结点及边,将所有桶分为层(为正整数),每层约有个桶,每层中的桶容量相同,第层桶容量约为n(表示图中当前结点数目)。 两种算法的区别在于桶容量:Small-buckets 算法桶容量小,故使用的总颜色数多,但是每次图更新后需要重染色的结点数目少;Big-buckets 算法桶容量大,故使用的总颜色数少,但是每次图更新后需要重染色的结点数目多。 但二者都不能保证在图更新过程中,使用的色数最少,且该算法依赖于静态图染色算法,在图更新过程中,多次调用静态图染色算法,使其效率较低。
2 基于批量更新的时间高效策略
2.1 DC-Batch 基本思想
本文基于DC-Global 算法,提出批量更新的优化策略,并提出DC-Batch 算法。 DC-Batch 基于OC图,可一次性处理所有更新边。 DC-Batch 算法主要思想为:
(1) 在无向图中新增和删除边。
(2) 更新OC 图。
(3) 处理度变化的结点。 若结点度增大/ 减小,将其加入中,并遍历其射入/ 射出结点,全序顺序改变的结点,有向边→(→) 变为→(→),将加入。
(4) 将中的结点重新染色。
当图G∗中任一结点颜色改变时(如图1),、旁边的数字代表其初始颜色,用、表示;(1) →(2) 表示的颜色从1 改变为2,改变后的颜色用表示。
、、之间的关系存在以下7 种情况:
(1)如图1(a):时,必须重新染色。
(2)如图1(b):时,可能染色为。
(3)如图1(c):时,可能染色为。
(4)如图1(d):时,不需重新染色。
(5)如图1(e):时,可能染色为。
(6)如图1(f) :时,不需重新染色。
(7)如图1(g):时,不需重新染色。
综上所述,当≠时,的颜色是否受到颜色变化的影响,取决于和。 若时,的颜色可能改变,否则颜色不会改变;当或者≠且时,需要重新染色。

图1 射出结点的染色Fig. 1 Coloring of the projected vertex
基于OC 图的染色方法,重要的是维护OC 图。插入或删除边时,会使图中结点度发生变化,结点的全序顺序会改变。 当结点的度增大或减小时,分别遍历其射入结点或射出结点,若全序顺序改变,则更新OC 图。
结点的颜色改变时,其射出结点有可能重新染色。 结点重新染色步骤如下:
(1)收集射入结点的颜色:对于图∗和任意结点,其射入结点颜色表示为集合。
(2)给当前结点染色:对于图∗和任意结点,利用集合中未使用的最小颜色为结点染色。
(3)射出结点重新染色:若颜色改变,则对其射出结点重新染色(即重复执行(1)、(2)步骤)。
2.2 算法描述
本文提出的DC-Batch 方法可同时处理新增边和删除边,并在保证染色效果的前提下,提高染色效率。 算法1 给出了基于OC 图的DC-BATCH 算法,展示了动态图中结点染色的具体步骤。
DC-BATCH 算法


3 基于批量更新的空间高效策略
3.1 算法思想
针对现有动态图染色方法空间消耗大的问题,本文提出DC-Simple 方法。 当新增/删除边时,用DC-Simple 对部分结点进行重新染色,染色结果与Global 方法保持一致。 对于OC 图中的任一结点, 有min{∈,∉∪};对于无向图,的颜色是全序排序在其之前的邻居结点未使用的最小颜色,即min{∈,∉∪v.color}。
对于图,不构建其OC 图,当新增或删除一条边(,) 后,则需要染色的结点包含以下3 部分:
(1)更新边的邻接结点和。
(2)更新前,全序排序在和前面,更新后在和后面的结点。
(3)更新前后, 全序排序都在和之后的结点。
3.1.1 新增边处理
综合上述3 种情况,需要重新染色的结点为{{,}∪I∪I∪I∪I}。 其中,I{≺
,∈} ∩{≺,∈(,)};I{≺,∈} ∩{≺,∈(,)};I{≺,∈} ∩{≺,∈(,)};I{≺,∈} ∩{≺,∈(,)}。
上文讨论了结点的度改变时,其射出结点颜色变化的情况。 这部分结点相当于I,所以继续沿用上文的分析结果,讨论当图中任一结点颜色改变时,I中结点的颜色变化情况。 如图2 所示,旁边的数字表示其颜色。 为表示方便,使用有向边表示全序排序,代表I中的任一元素。 如图2(a)所示,表示结点全序顺序在结点之前。 用表示结点的初始颜色,用表示重染色后的颜色(同理)。 当任意结点的颜色改变时,射出结点是否重新染色需根据以下情况判定:
(1)如图2(b),。 此时,必须重染色。
(2)如图2(c),。 此时,颜色不改变。
(3)如图2(d),。 此时,颜色不改变。

图2 Iu1中结点重新染色Fig. 2 Vertices recoloring inIu1
3.1.2 删除边处理
综合上述3 种情况,需要重新染色的结点为{{,} ∪D∪D∪D∪D}。 其中,D{≺,∈}∩{≺,∈(,)};D{≺,∈} ∩{≺,∈(,)};D{≺,∈} ∩{≺,∈(,)};D{≺,∈} ∩{≺,∈(,)}。
根据上述分析,当删除边(,) 时,应先对和的部分邻居结点重新染色,再对结点和结点重新染色。 因为更新后,有一些结点全序排序在其前面。D为和的部分邻居结点,和相邻,则二者颜色不同,需要重新染色的情况为:
(1)如图3(b),。 此时的颜色不会改变。
(2)如图3(c),,此时可能需要重新染色。

图3 Du1中结点重新染色Fig. 3 Vertices recoloring inDu1
DC-Simple 算法对新增边和删除边分别使用DC-Simple-Ins 和DC-Simple-Del 来处理。 DCSimple-Ins 思想是,当新增边,时,将结点和放入中,依据全序顺序来排序,全序排序在前的结点优先级更高。 对中的每个结点,遍历其邻居结点并分为3 部分:
(1)全序排序在之前的结点,收集这些结点的颜色,并找出其未使用最小颜色。
(2)更新前全序排序在之前,更新后全序排序在之后的结点。 当满足时,加入。
(3)更新前后全序排序都在之后的结点。当满足时加入。
3.2 算法描述
DC-Simple 与DC-Batch 方法最大的区别是未使用OC 图。 DC-Simple 可以在保证染色效果的前提下,降低空间复杂度,解决了DC-Batch 方法空间复杂度高的问题。 算法2 给出了DC-Simple-Ins 方法实现过程。
DC-Simple-Ins 算法

无向图及其根据Global 方法得到的染色结果如图4 所示。 根据DC-Simple-Ins 算法分析,当在图新增边(,),则将{,} 加入中。 首先遍历的邻接结点,发现的全序顺序比其所有邻接结点都大,故c为0,无需重新染色。 之后遍历的邻接结点,由于的度大于, 所以c为1,可使用的最小颜色为1,则的重新染色为1。 因为的颜色改变,所以将、加入中。 然后依次对中的结点重新染色。 最终的染色结果如图5 所示。

图4 无向图GFig. 4 Undirected graph G

图5 无向图G+(v5,v8)Fig. 5 Undirected graphG+(v5,v8)
DC-Simple-Del 算法序顺序在后的结点加入中


4 实验结果分析
4.1 实验环境
本文实验环境为:Intel Core i5 主频为2.50 GHz的CPU;Windows 7 的32 位操作系统;运行内存4 GB;开发环境为Microsoft Visual Studio 2013,使用C++语言实现代码。
4.2 数据集及评价指标
数据集来自KONECT,本文在4 个真实数据集上进行实验。 其中,MovieLens 为美国的电影评价网站;DBLPwe 为文献网站;Flickr 为社交网络图;Amazon 为美国的电商平台。
表1 为数据集信息。 其中,为结点数;为边数;表示图中结点的最大度。 本节将从染色质量、染色效率、内存消耗3 个方面对DCBatch、DC-Simple 和DC-Local、DC-Global 算法进行对比分析。

表1 真实数据集统计信息Tab. 1 Real data sets statistics
4.3 性能比较分析
4.3.1 染色质量对比分析
在实验中,保留每个数据集5%边作为初始图,以保证本文算法具有良好的可扩展性。 每次增加30%的边,记录色数。 4 个数据集上的色数如图6 ~图9 所示。 由图6 和图8 可知:对于MovieLens 和DBLP,随着边的增加,DC-Local 算法的色数快速增长,其它方法的色数保持稳定。 由图7 和图9 可知:对于Baidu 和Flickr,随着边的增加,DC-Local 与其它算法使用的色数都会快速增加,但DC-Local 的增加速率最快。
4.3.2 染色效率对比分析
首先使用Global 算法对每个数据集染色,之后在每个数据集上随机增加和删除10 000 条边,计算出处理一条边的平均运行时间并进行对比。 3 个算法的运行时间如图10 所示。 在所有数据集上,DCBatch 比DC-Global 运行时间短,表明批量更新策略更高效。 在MovieLens 上,DC-Simple 运行时间比DC-Batch 短;在其他数据集上,DC-Simple 和DCBatch 运行时间几乎相同,这说明DC-Simple 效率也比较高。
4.3.3 内存消耗对比分析
内存消耗在Flickr 和Baidu 上进行实验,其结果如图11 所示。 可以看出,在Flickr 上DC-Simple与DC-Batch 的内存消耗峰值分别是1 000 MB 和1 200 MB;在Baidu 上DC-Simple 与DC-Batch 算法的内存消耗峰值分别是8 980 MB 和1 300 MB。 证明DC-Simple 比DC-Batch 内存消耗更低。 这是因为,DC-Batch 算法基于OC 图,而DC-Simple 算法不使用OC 图,节省了构建OC 图的内存消耗及OC图本身占用的内存消耗。
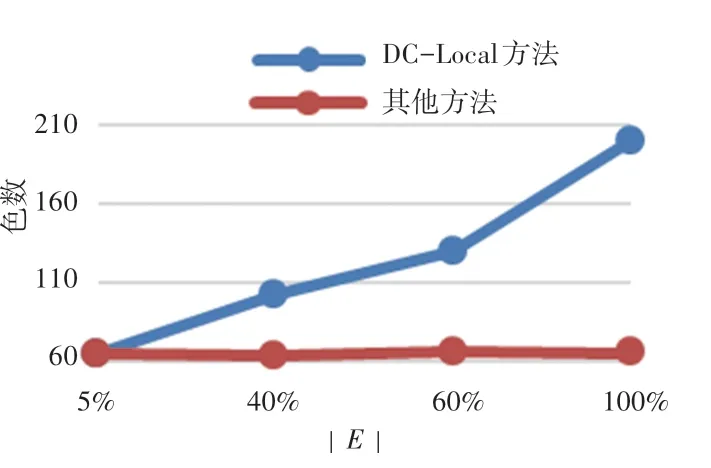
图6 MovieLens 数据集染色质量图Fig. 6 Coloring quality chart of MovieLens

图7 Baidu 数据集染色质量图Fig. 7 Coloring quality chart of Baidu
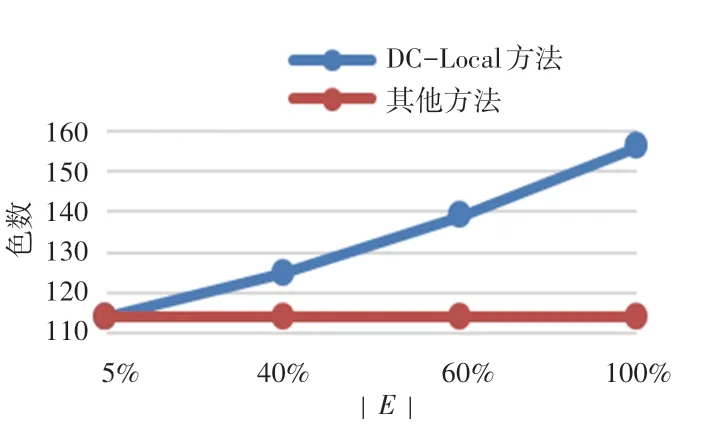
图8 DBLP 数据集染色质量图Fig. 8 Coloring quality chart of DBLP

图9 Flickr 数据集染色质量图Fig. 9 Coloring quality chart of Flickr

图10 各算法平均运行时间图Fig.10 Average running time of each algorithm

图11 内存消耗峰值比较图Fig.11 Memory consumption peak comparison chart
5 结束语
针对现有算法染色效率低、内存消耗大的问题,本文提出批量处理更新的高效染色方法DC-Batch。该算法并不关心图更新时的中间状态,而是针对一段时间图更新的最终状态,一次性处理所有的更新,减少重复处理结点的操作,提高处理效率。 同时,提出了高效的结点剪枝策略来加速计算,在保证染色质量的前提下,染色效率平均提高50%。 针对已有方法索引占用空间大的问题,提出无需维护额外索引的结点剪枝策略,以及基于此策略的DC-Simple方法。 该方法针对所有更新边,根据结点的度来动态维护结点的处理顺序。 实验结果表明,DCSimple 方法与DC-Batch 方法相比,在保证染色效果的同时,内存消耗平均降低24%。
