基于粒子群算法的边界盒定位改进算法研究
2022-05-05沈静静王恩亮王亓剑
沈静静,程 浩,王恩亮,姚 玲,王亓剑,章 华
(1.安徽新华学院电子工程学院,安徽 合肥230088;2.海鹰企业集团有限公司,江苏 无锡 214000)
0 引言
边界盒(Bounding-box)定位算法是由Simic和Sastry提出的一种依靠自身通信范围内信标节点的位置和通信半径的非测距定位算法[1]。该算法通过计算正方形交集区域的质心,作为未知节点的坐标,定位误差相对较大。粒子群(Particle Swarm Optimization,简称PSO)算法是启发于现实生活中鸟群寻食路线而提出的一种算法,其具有群体化优化的特点,通过群体和个体的不断修正、优化,从而来求出最优的解[2]。Shi等在1998年提出带有惯性权重的标准粒子群算法,惯性权重较小时可以取得较好局部解,惯性权重较大时有较好的全局搜索能力[3]。该算法得到了广泛的应用,并取得了较好的效果[4-6]。为此,本文给出一种粒子群算法改进的边界盒定位算法,同时对该方法进行了仿真实验,与边界盒定位算法进行了比较。通过Matlab仿真发现,基于粒子群算法的边界盒定位改进算法的精度值比单独的边界盒子定位要有所增加。
1 粒子群算法
粒子群算法通过数学建模“飞行”函数,函数中相关参数——全局最优解(指当前时刻搜索整个群体中的最优值)和个体最优解(指当前单个粒子搜索到的最优值)最优解的选择是通过与适应度函数的匹配度来获得粒子的质量程度。它的基本原理为:大小数量为M个的粒子群,存在于N维的搜索空间中,则第i个粒子的位置可以被描述为Xi=(xi1,xi2,…,xiN),“飞行”速度Vi=(vi1,vi2,…,viN),搜索到目前时刻的最优解为Pbest=(pi1,pi2,…,piN)(i=1,2,…,M),整个种群搜索到目前时刻全局最优解Gbest=(g1,g2,…,gN)[7]。第t次搜索后将按照公式(1)和(2)分别更新速度和位置。
Vij(t+1)=ω×Vij(t)+C1rand( )[pij(t)-xij(t)]+
C2rand( )[gij(t)-xij(t)]
(1)
xij(t+1)=xij(t)+Vij(t+1)
(2)
式(1)(2)中:j为粒子的维度参数;ω为惯性权重参数;rand()表示在[0,1]的随机常数值;C1、C2为学习因子,通常取C1=C2=2。
2 边界盒定位算法
边界盒算法是通过通信范围内信标节点以及其通信半径求得未知节点所在估计区域,本文结合图1,对边界盒定位算法的核心思想进行阐述[8]。假定图1中每个节点的通信半径都为R,实心圆心为信标节点,空心圆心为未知节点。定位过程如下。
1)未知节点向半径为R范围内的信标节点发送定位信息的请求信号。
2)信标节点收到请求后,发出自己的相关信息。
3)未知节点收到信标节点发送的信息后,就知道自己位于哪些信标节点通信范围的外切正方形(与2个坐标轴平行)的交集区域内(长方形ABCD)。例如未知节点通信范围内有N个信标节点,(xi,xi),(xj,xj),其中i=1,2,…,N;j=1,2,…,M为信标节点坐标,则正方形交集区域为:
[max(xi,xj)-R,min(xi,xj)+R]×[max(yi,yj)-R,
min(yi,yj)+R](i=1,2,…,N)
(3)
(4)
该算法计算比较容易,但对通信范围内的信标节点密度有很大的依赖性,且定位误差大。

图1 边界盒算法平面示意
3 粒子群算法改进的边界盒定位算法
粒子群算法(PSO)采用速度-位置的并行搜索模型,可以通过粒子群算法在交集区域内进行搜索进一步提高定位精度。粒子群算法具有较强的随机性,即使算法参数相同,结果也会不同,但是可以通过各参数的合理搭配获得较高精度的解。
3.1 惯性权重
从式(1)中可以看出,Vi(N-1)对ViN的影响程度由惯性权重ω控制。基于粒子群算法的边界盒子定位改进算法采用的惯性权重线性递减算法[3],表达式为:
(5)
式中:Tmax为最大迭代次数;T则是目前最新的迭代数。通过实际前期实验可知,可设ωmax的值为0.9,ωmin的值为0.4。
已知通过前期实验,群体粒子个数和精度不是正比关系。粒子个数越多,搜索区域就越大,越易获得全局最优解[9]。粒子个数应根据具体问题来选择。
3.2 粒子位置
为了继承边界盒算法的优点,在边界盒定位法中,通过式(3)可以得到边界盒定位算法的交集区域。该区域的确定减少了搜寻区域,可以确定粒子每一维的范围为:
(6)
式中:i=1,2,…,N;j=1,2,…,N。
将其中一个粒子的初始位置定在由式(4)计算所得出坐标的位置,其余粒子进行随机分布,如图2所示。

图2 粒子初始位置平面示意
另外,当粒子位置某一分量(方向、距离、角度等参数)在飞行中超出搜索空间时,可以对粒子这一分量进行限制。以第一个分量为例,假设第n个粒子的第一个分量为xn,公式[10]如式(7)所示:
xn(xn>xmax|xn (7) 式中:xmax和xmin分别为对应分量参数的最大值和最小值。 通过将粒子速度控制在[-vmax,vmax]中[11],从而减少粒子在空间内的无规则跳动。因为若粒子速度过大,其飞过最优解的概率会增大,若粒子速度过小,则可能使其出现局部极值的问题。本文中,将粒子的最大速度vmax设置为问题空间的50%。粒子的初始速度在[-vmax,vmax]内随机生成。当粒子速度某一分量飞行中超出速度范围时,可以对这速度一分量进行限制。以第一个分量为例,假设第n个粒子飞行速度的第一个分量为vn,公式如下: vn(vn>vmax|vn (8) 通过构建适应度函数的方法,其目的是为降低累积定位误差。其相关原理为:未知节点在其通信范围内若有N个信标节点,则第n个未知节点到N个信标节点的欧式距离dn为: (9) 式中:i=1,2,…,N。 通过测距方法可分别测得未知节点到通信范围内信标节点间的距离di,则适应度函数为: (10) 式中:i=1,2,…,N。 本文在构建适应度函数时,只随机选取通信m(m≤3)个信标节点综上所述,适应度函数可以构造为: (11) 式中:i=1,2,3。 步骤1:通过边界盒核心思想获得交集区域。 步骤2:初始化算法。设置区域内粒子的初速度和初位置,并将算法中的相关参数初始化操作。 步骤3:根据各粒子当前位置,以公式(11)计算每个粒子的适应度值F(xi),比较适应度值获取个体最优解(Pbest)、全局最优解(Gbest)。 步骤4:根据式(1)(2)得到当前的位置和速度。 步骤5:持续观察当前的迭代次数是否大于等于最大迭代次数或者其误差达到要求范围,若不满足,则返回步骤3继续迭代。若满足,则输出最优位置,即为未知节点坐标。 为了模拟真实环境中的干扰因素,在该仿真实验中使用的测量距离为2节点间真实距离加上正态分布随机误差[13-14],采用服从正态分布N(0,(0.05di)2)。定位区域范围为边长为100 m的正方形。 定位误差为未知节点的误差总和与通信距离、实验次数和未知节点个数的乘积的比值。假设未知节点的估计坐标为(x′,y′),未知节点的真实坐标(x,y),通信距离为R,实验次数为N,未知节点数为M。则定位评价的标准E为: (12) 在定位范围内随机设置100个节点,并设置初始信标节点(锚节点)为10个,并以增长量为5逐步增加信标节点个数。在信标节点数量下重复进行150次实验,每次实验重新随机产生节点。设置通信范围为40 m,初始粒子群个数为10,迭代次数设为10。仿真结果如图3所示,定位误差随信标节点的增加存在波动,但是粒子群算法改进的边界盒定位算法(psoBounding-box)定位精度比边界盒定位算法(Bounding-box)更高。 图3 信标节点个数与定位误差关系 定位范围内随机设置100个节点,并设置其中30个为信标节点,通信范围设为40 m。初始粒子群数目为10。迭代次数从5次增加到50次,每次增加5次,每个迭代次数下重复进行150次实验。每次实验重新随机产生节点。仿真结果如图4所示,粒子群算法改进的边界盒定位算法可以在迭代后获得相对更低的定位误差。定位误差随迭代次数的波动也说明了粒子群算法改进的边界盒定位算法的特性。 图4 迭代次数与定位误差关系 另外,粒子群算法的迭代必然会增加计算量,所有边界盒定位算法的改进算法与其基本算法相比,都增加了计算量,以计算量的增加为代价换取更高的定位精度。因此,在实际应用中,选择定位算法时应根据具体要求。 定位区域内随机分布100个节点,信标节点为30个,初始粒子群数目为10,迭代次数为10。通信范围从10 m增加到40 m,每次增加5 m。在每个通信范围下重复进行150次实验。每次实验重新随机产生节点。仿真结果如图5所示,2种定位算法的误差都随通信范围的增加而减小,但是粒子群算法改进的边界盒定位算法定位精度比边界盒定位算法更高。 图5 通信范围与定位误差关系 本文在边界盒定位的基础上,提出通过粒子群算法对正方形交集区域进行并行搜索来提高定位精度的方法。粒子群算法的边界盒定位改进算法在信标节点相同条件下,定位误差小于边界盒算法,且误差很接近0,在相同的通信范围内,粒子群算法的边界盒定位改进算法的误差小于边界盒定位算法,所以,综合而言,基于粒子群算法的边界盒定位改进算法提高了定位精度,具有一定的改进效果。3.3 粒子速度
3.4 适应度函数
3.5 粒子群算法改进的边界盒定位算法分析步骤
4 仿真实验
4.1 定位误差与信标节点个数

4.2 定位误差与迭代次数
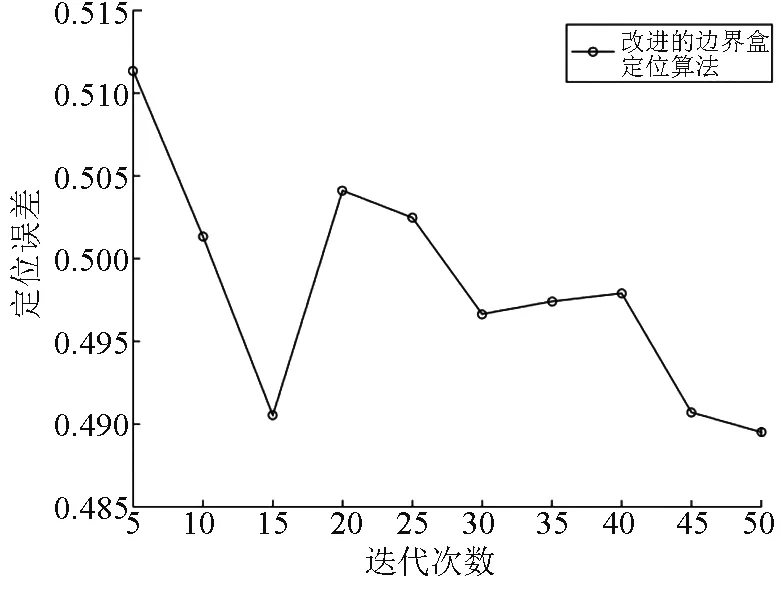
4.3 定位误差与通信范围
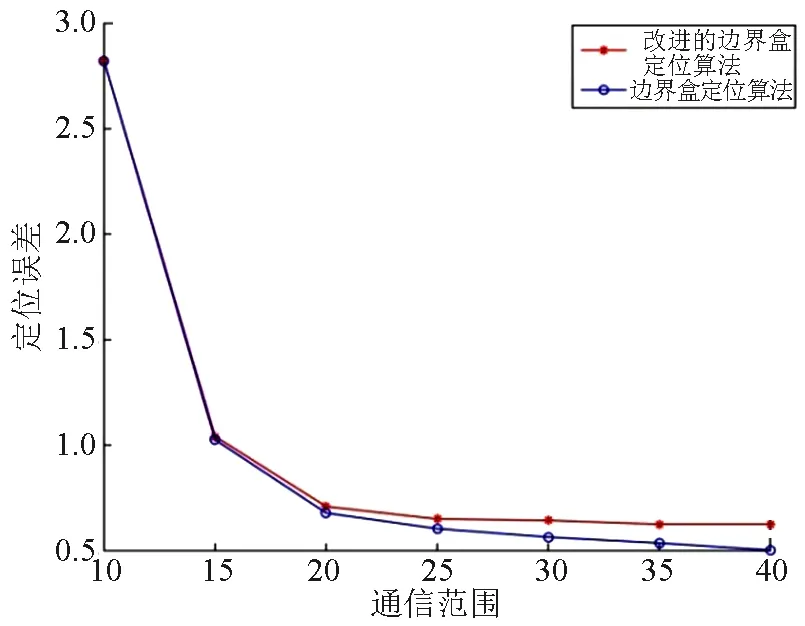
5 结语
